R3上一類特殊Besicovitch集的維數(shù)估計(jì)
陳澤斌
(汕頭大學(xué)數(shù)學(xué)系,廣東 汕頭 515063)
1 引言
Kakeya在1917年提出了尋找單位直線段可以在其內(nèi)部調(diào)轉(zhuǎn)方向并且具有最小面積的平面集的問(wèn)題,也就是連續(xù)地移動(dòng)此單位直線段而不離開(kāi)此集使它旋轉(zhuǎn)180?并回到原來(lái)位置,這個(gè)問(wèn)題基本上可歸結(jié)為尋找包含每個(gè)方向單位直線段的最小區(qū)域的問(wèn)題.1928年,Besicovitch發(fā)現(xiàn)了一個(gè)平面上的單位直線段可以在其內(nèi)部轉(zhuǎn)到相反方向,但其面積卻可以任意小的令人驚奇的集的構(gòu)造.即有如下定理.
定理1.1有一個(gè)面積為零的平面集,它在所有方向上都包含一單位直線段.
上述定理的證明參考文獻(xiàn)[1].Rn中在每個(gè)方向包含有一個(gè)直線段的集合稱為Besicovitch集,定理1.1證明了R2中存在Besicovitch集;取這種集與Rn?2的乘積集,就得到了Rn上的Besicovitch集.隨著這個(gè)問(wèn)題的解決,一個(gè)很自然的問(wèn)題擺在眼前,就是如下著名的Kakeya猜想.
猜想Rn空間中的任意Besicovitch集的Hausdorff維數(shù)等于n.
關(guān)于Kakeya猜想,國(guó)際上已經(jīng)有很多數(shù)學(xué)家(如Wolff,Bourgain,Tao等)做了大量的工作,其中n=2的情形已完全解決,并存在好幾種證明方法(見(jiàn)文獻(xiàn)[1–3]).而對(duì)于高維(n≥3)的情形,雖然目前還沒(méi)得到徹底解決,但是有許多著名的數(shù)學(xué)家做出了本質(zhì)的推進(jìn).1985年,Christ-Duoandikoetxea-Rubio de Francia[4]首先證明了下界為.1991年,著名數(shù)學(xué)家Bourgain[3]利用一個(gè)稱為“bush”的構(gòu)造將其改進(jìn)為這里εn是一個(gè)固定的數(shù),只與n有關(guān).而這項(xiàng)工作最突出的結(jié)果來(lái)自于Wolff[5],1995年Wolff利用另一個(gè)稱為“hairbrush”的更有效的構(gòu)造再次將這個(gè)下界提高至,其中對(duì)于3≤n≤8.這仍然是目前最好的結(jié)果.而對(duì)于n≥9,之后Katz–Tao[6]于2000年將其提高至.
由上述可知在高維空間Kakeya猜想雖然已得到豐富的結(jié)果,但是可以看到,即使是n=3的情形,最好的結(jié)果也僅是2.5,距離最終結(jié)果3還差了很多.針對(duì)n=3,利用已有的構(gòu)造和方法要想進(jìn)一步提高這個(gè)下界是相當(dāng)困難的.那么一個(gè)比較自然的想法是,若僅對(duì)一類特殊的Besicovitch集進(jìn)行維數(shù)估計(jì),能否推出這類Besicovitch集的Hausdorff維數(shù)等于3呢?本文以此作為出發(fā)點(diǎn).將Kakeya問(wèn)題二維情形的一種證明方法(參考文獻(xiàn)[2])推廣到R3空間,接下來(lái)將定義一類圓盤(pán)型Besicovitch集,具體如下.
定義1.1令E為Rn中的圓盤(pán)型Besicovitch集,E包含以所有ξ∈Sn?2(n≥3)為法向量,點(diǎn)a為圓心的各個(gè)方向的單位圓盤(pán),即E={x∈Rn:|(x?a)|≤1,(x?a)·ξ=0}.為方便起見(jiàn),將這類型的Besicovitch集簡(jiǎn)記為E集.下面是與之相關(guān)的δ-圓盤(pán)概念:
定義1.2令0<δ?1,對(duì)E中任一方向的圓盤(pán),給其增加δ厚度,使其成為一個(gè)δ-圓盤(pán),記為即這里x⊥=x?(x·ξ)·ξ.
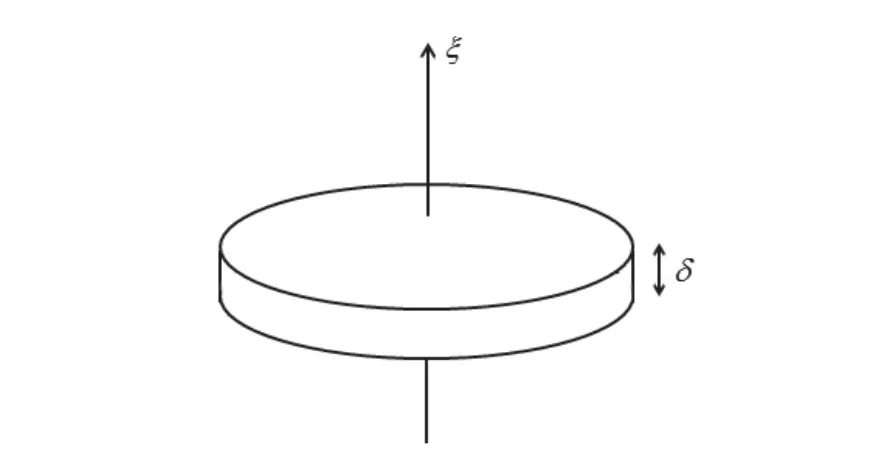
圖1:δ-圓盤(pán)
2 主要結(jié)論
回顧了Kakeya猜想的研究背景和研究現(xiàn)狀,針對(duì)上面定義的圓盤(pán)型Besicovitch集,本文的主要結(jié)論如下.
定理2.1R3上的E集的Hausdorff維數(shù)為3.
3 預(yù)備知識(shí)
在這一節(jié),將介紹Hausdorff維數(shù)和δ-分隔子集的概念,并做一些符號(hào)的約定.
定義3.1令E∈Rn,α>0,對(duì)0<δ≤1,定義這里κδ是E的可數(shù)覆蓋,由半徑ri<δ的小球B(xi,ri)構(gòu)成的集合,即
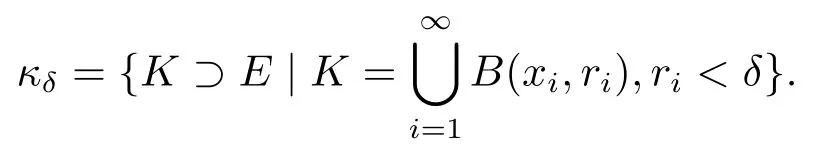
令δ→0,得到E的α-Hausdorff測(cè)度
對(duì)任意E∈Rn,為α的非增函數(shù).一步,若α<β,則從而若Hβ(E)>0,則Hα(E)>0為無(wú)窮.因而存在唯一的數(shù),記為dimHE,稱為E的Hausdorff維數(shù),滿足若0≤α 定義3.2令E∈Rn,S?E,若任意不同的兩點(diǎn)x,y∈S滿足|x?y|≥δ,那么稱S為E的δ-分隔子集. 為了方便敘述,做如下約定 (1)表示集合A中元素的個(gè)數(shù); (2)對(duì)于f和g兩個(gè)函數(shù),fg表示存在常數(shù)C,獨(dú)立于f和g,使得f≤Cg. 所以 故 結(jié)合定理4.1和定理4.2,即得定理2.1. 本文在R3空間定義了一類圓盤(pán)型Besicovitch集并對(duì)其進(jìn)行維數(shù)估計(jì),證明了該圓盤(pán)型Besicovitc集的Hausdorff維數(shù)為3.因?yàn)镵akeya二維情形已有的證明方法無(wú)法推廣到高維空間上,所以接下來(lái)將會(huì)致力于尋找高維情形新的證明方法.4 定理2.1的證明


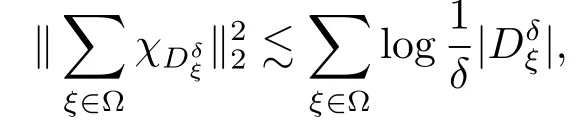
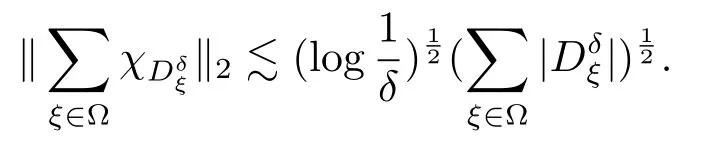
5 結(jié)論
- 數(shù)學(xué)雜志的其它文章
- 多線性分?jǐn)?shù)次積分及其極大算子在變指標(biāo)Herz空間上的有界性
- 基于蒙特卡洛方法的非負(fù)矩陣分解初始化
- THE COMMUTATOR TYPE AND THE LEVI FORM TYPE IN C3
- REGULARIZATION METHOD FOR AN ILL-POSED CAUCHY PROBLEM OF NONLINEAR ELLIPTIC EQUATION
- THE α-BERNSTEIN OPERATOR OF A LIPSCHITZ CONTINUOUS FUNCTION
- INTEGRAL FORMULAS FOR COMPACT SUBMANIFOLDS IN EUCLID SPACE

