REGULARIZATION METHOD FOR AN ILL-POSED CAUCHY PROBLEM OF NONLINEAR ELLIPTIC EQUATION
ZHANG Hong-wu,ZHANG Xiao-ju
(School of Mathematics and Information Science,North Minzu University,Yinchuan 750021,China)
Abstract:This paper considers an ill-posed Cauchy problem of nonlinear elliptic equation.By using a regularization method to overcome the ill-posedness,we obtain the existence,uniqueness,stability and convergence result of the regularization solution,and an iterative scheme is constructed to calculate the regularization solution,which is an extension on the related research results of existing literature in the aspect of regularization theory and algorithm for Cauchy problem of elliptic equation.
Keywords:ill-posed problem;Cauchy problem;nonlinear elliptic equation;regularization method
1 Introduction
The direct problems for elliptic equations(Dirichlet,Neumann or mixed boundary value problems)extensively studied.However,in some practical problems,the whole boundary data often can not be known,we only know the noisy data on a part of the boundary or at some interior points of the concerned domain,which will lead to some inverse problems.
This paper considers the following inverse problem of nonlinear elliptic equation
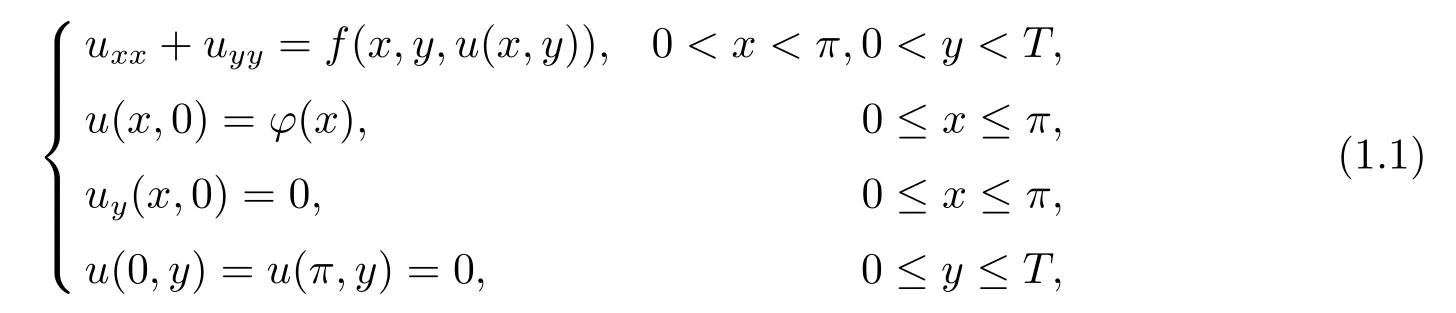
where?(x)∈L2(0,π)is known function,f:R×R×L2(0,π)→L2(0,π)is an uniform Lipschitz continuous function,i.e.,existingL>0 independent ofx,y∈R,u,v∈L2(0,π),such that Our assignment is to determineu(·,y)from(1.1)–(1.2).
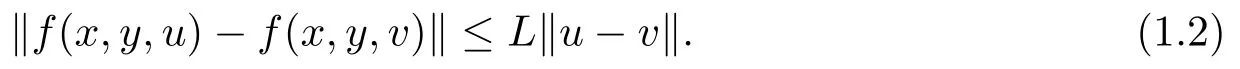
This problem is called the Cauchy problem.Asf(x,y,u)=?k2u,it is the Helmholtz equation that has important applications in acoustic,hydrodynamic and electromagnetic waves[1,2],etc.Iffis independent ofu,it becomes as the Poisson equation.If settingf(x,y,u)=sinu,we deduce that the classical nonlinear elliptic sine-Gordon equation which mainly appears in the theory of Josephson effects,superconductors,spin waves in ferromagnets,see[3,4].
Problem(1.1)is ill-posed in the sense that the solution(even if it exists)does not depend continuously on the given Cauchy data[5,6].It causes great difficulty in doing the numerical calculations,thus some special regularization techniques are required to stabilize numerical computations,see[6,7].Note that,asf=0,the problem is the Cauchy problem of Laplace equation,many regularization methods were presented to study it in past years,such as the quasi-reversibility method[8–11],Tikhonov method[12],discretization method[13,14],the fundamental solution method[15],non-local boundary value problem method[16,17],etc.In 2014–2018,[18–21]respectively used modified boundary Tikhonov-type,Fourier truncated,filtering function and Generalized Tikhonov-type regularization methods to solve the abstract Cauchy problem of semi-linear elliptic equation in the general bounded domain.On the other similar works for the Cauchy problem of nonlinear elliptic equation,please see[22–28].
In 2012,[29]considered the Cauchy problem of Laplace equation
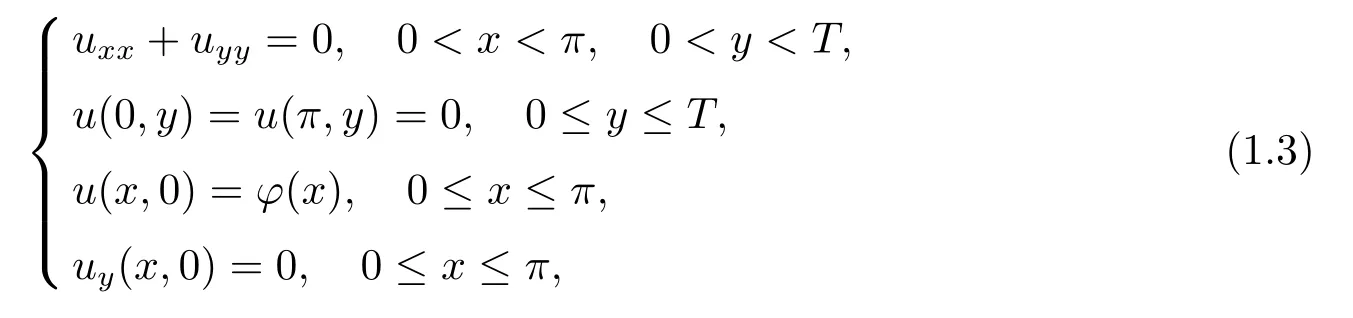
and forp≥1,we defined the regularization solution as
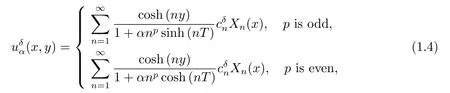
i.e.,the so-called improved non-local boundary value problem method,whereandis an orthonormal basis ofL2(0,π),?δdenotes the measured data and satisfies,denotes theL2-norm andδ>0 is a noise level,αis the regularization parameter.Inspired by this method,in the present paper we investigate the nonlinear problem(1.1)–(1.2)and adopting a similar technique to overcome its ill-poseness(see Section 2),this is an extension to the work in[29].
The article is constructed as below.Section 2 uses our method to treat problem(1.1)and proves the well-posedness of regularized problem.In Section 3,the convergence estimate for this method is derived.An iterative scheme is proposed to calculate the regularization solution and make some numerical verifications in Section 4.Some conclusions are given in Section 5.
2 Regularization Method and some Well-Posed Results
2.1 Regularization Method
Adopting the similar method as in[19],we can derive that the unique solution to problem(1.1)satisfies the nonlinear integral equation
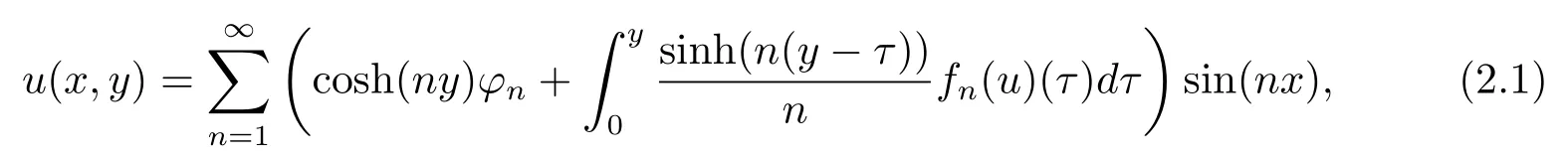
where
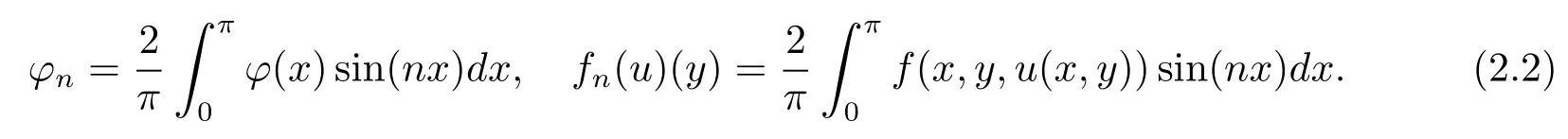
(2.1)means that cosh(ny),sinh(n(y?τ))/n→∞(n→∞),so in order to restore the stability of problem(1.1),we must eliminate the high frequency parts of two functions to design the regularization solution of original problem.
Based on the analysis above and considering the compatibility of physical dimension,whenp≥1 is even,we approximate the nonlinear problem(1.1)as
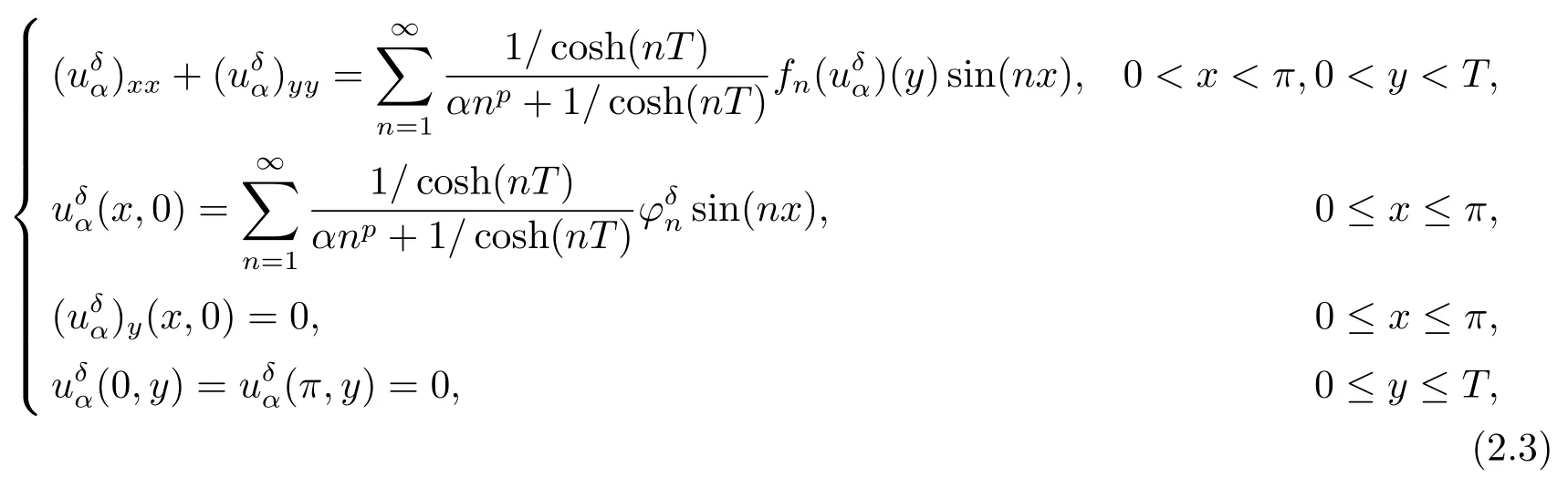
whenp≥1 is odd,it is regularized by
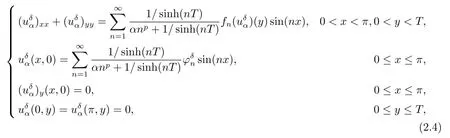
where
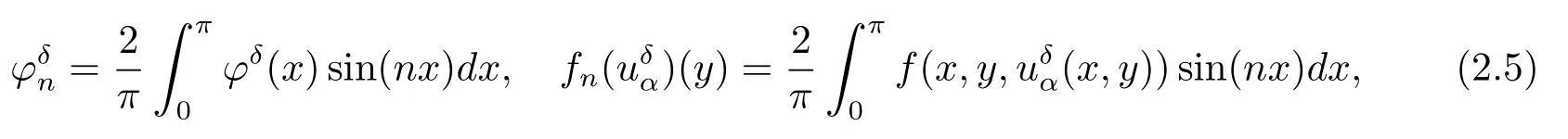
andα>0 is the regularization parameter,the measured data?δ∈L2(0,π)satisfiesis the error level,denotesL2-norm.In fact,it is easily verified that the solution to problem(2.3)satisfies the nonlinear integral equation
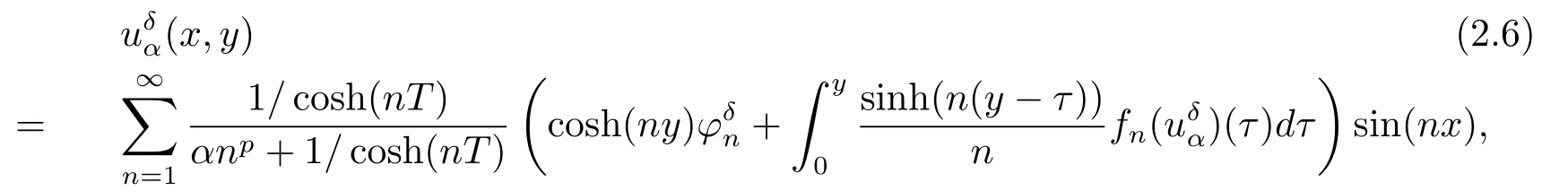
the solution of problem(2.4)satisfies the nonlinear integral equation
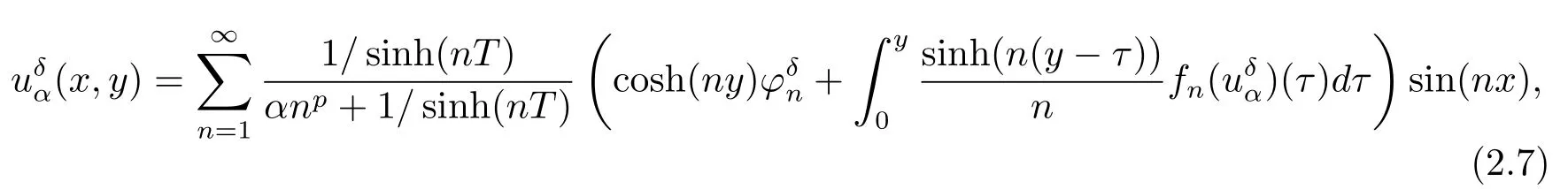
2.2 Some Well-Posed Results
According to the regularization theory,in order to ensure that the regularization solution is a stable approximation to exact solution,we need proof the existence,uniqueness,and stability for the solution of(2.6)and(2.7).
Now,letx>0,0≤τ≤y≤T,we define two functions
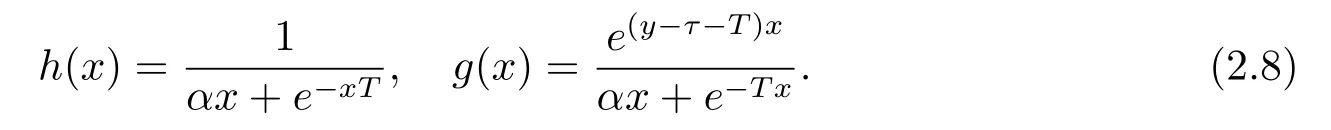
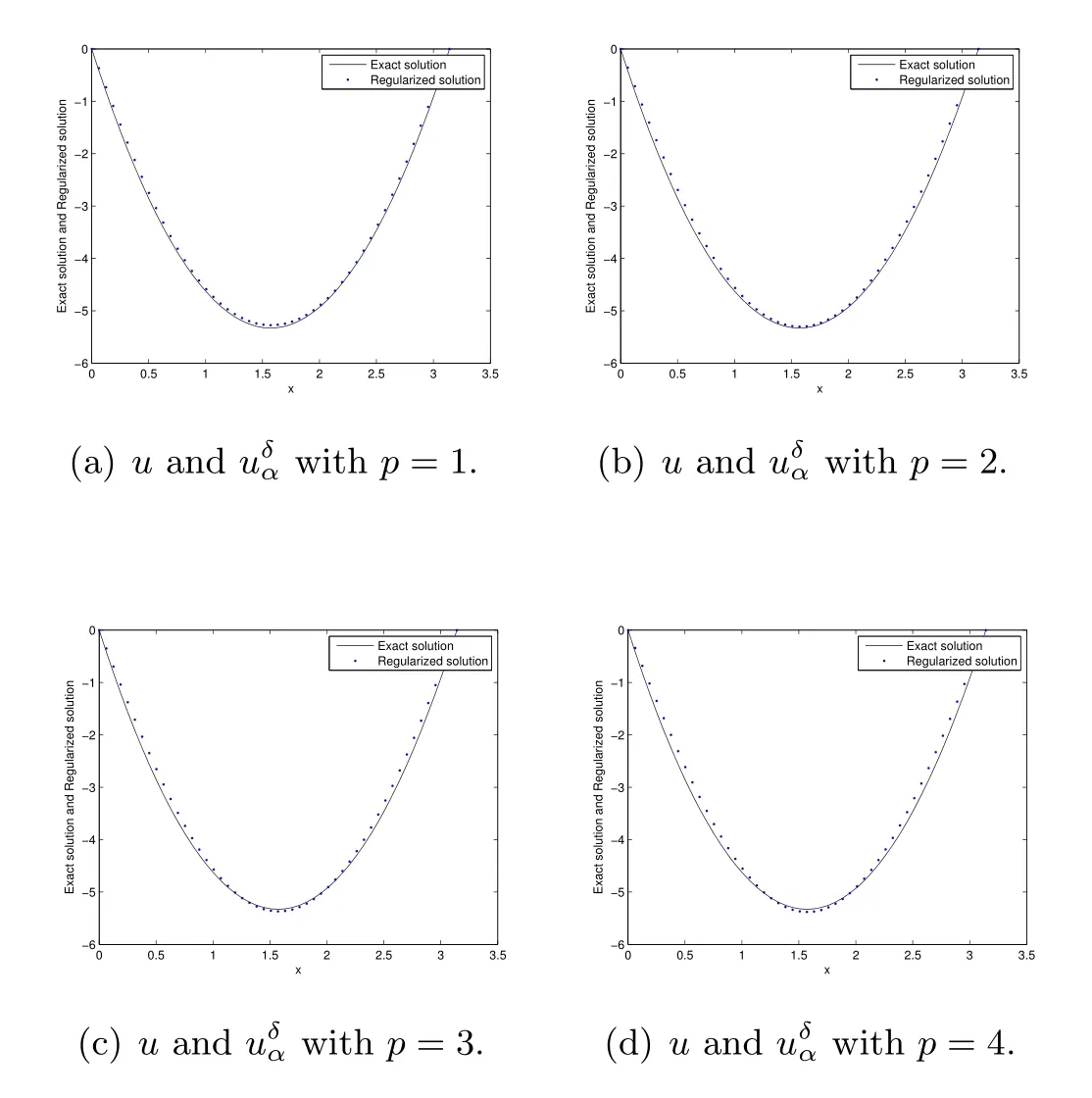
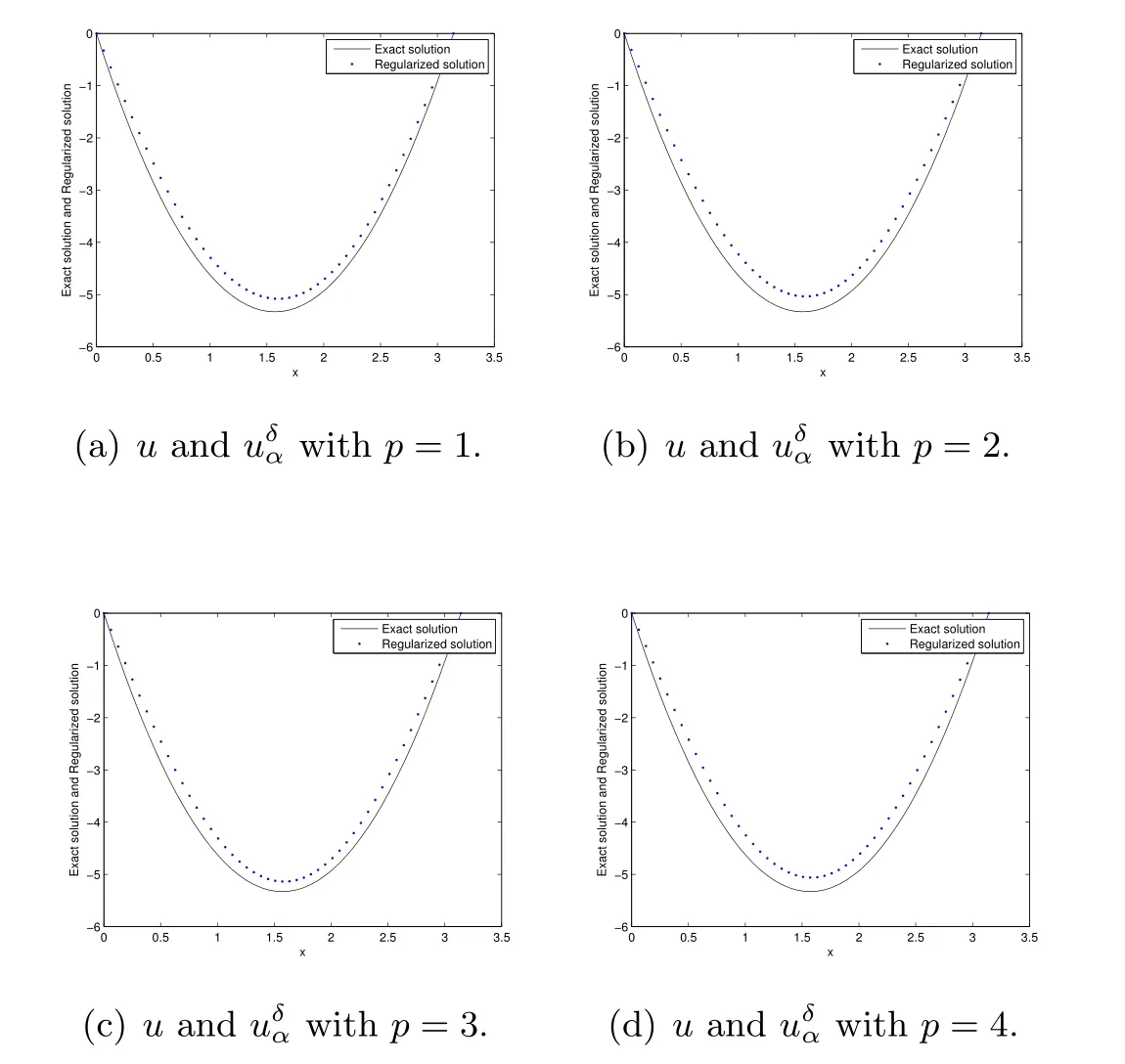
Noting that whenα and it is also proved that clearly,whenτ=0,we have ProofForw∈C([0,T];L2(0,π)),we define the operator Γ(w)(·,y)as then forw,v∈C([0,T];L2(0,π)),q≥1,we prove the following result whereCα=T/α,denotes the sup norm inC([0,T];L2(0,π)).First,we use the induction method to derive the following estimate Forq=1,from(2.12),(2.9)and(1.2),ande(y?τ?T)≤1,we can get Whenq=i,suppose that then forq=i+1,by(2.15),and use the similar process,we obtain that Then Using Gronwall’s inequality[30],it can be obtained that For some time he stumbled along, keeping to the path as well as he could in the darkness, and just as he was almost wearied out he saw before him a gleam of light From(2.22),estimate(2.19)can be established. Theorem 3.1Suppose thatuis the solution of problem(1.1)andis the solution of problem(2.6).Let the measured data?δsatisfy,and the exact solutionusatisfy and the regularization parameterαis chosen as then for fixed 0 ProofDenotinguαas the corresponding solution of problem(2.6)with the exact data?.Using the triangle inequality,we have From Theorem 2.2,we get By(2.1),(2.6),(2.10),(2.11),(3.1),and use the inequalityet/2≤cosh(t)≤etfort>0,it can be derived that Remark 3.3In the research of ill-posed problems,we often impose an a-priori assumption on the exact solution to make the convergence estimate of one regularization method.For our problem,the difficulty of imposing the a-priori assumption mainly lie in the nonlinear property and the application of regularization method.In view of the factors above,here we impose a-priori assumption(3.1),(3.11),and combine with(2.10),(2.11)to proof Theorems 3.1–3.2. Remark 3.4Our given method can be applied to investigate the cases of nonhomogeneous Neumann data(u(x,0)=0,uy(x,0)=φ(x)0)or nonhomogeneous Dirichlet and Neumann datum(u(x,0)=?(x)0,uy(x,0)=φ(x)0).Since the constructed procedure of regularization method is similar with the one in Subsection 2.1,here we skip it. In this section,an iterative scheme is proposed to calculate the regularization solution and a numerical example is performed to verify the efficiency of our method.Consider the nonlinear problem It is clear thatu(x,y)=x(x?π)(2+y2)is an exact solution of problem(4.1),thusg(x,y)=2x(x?π)+2(2+y2)?cos(x(x?π)(2+y2)),?(x)=u(x,0)=2x(x?π),and the measured data is given by?δ(x)=?(x)(1+ε(x/2?1)). Let 0=y0 here,for the case thatpis even,,whenpis odd,,and Adopt the above algorithm,we choosewithM=50,fork=1,2,···,50,j=1,···,m=5 to computeaty=0.4,1(k=20,50).In the computational procedure,the regularizationαis chosen by(3.2)or(3.12).Forp=1,2,3,4,the numerical results forε=0.01 are shown in Figure 1–2,respectively.Forp=1,2,3,the relative root mean square errors between the exact and regularization solutions are defined by the computed results are shown in Table 1. Figure 1–2 and Table 1 show that our proposed method is effective and stable.Meanwhile,we note that the more smallεis,the better the calculation effect is,this is a common phenomenon in the computation of ill-posed problems.Table 1 indicates that the computational effect of our method is more better whenpis an odd.Finally,we mention that the iteration scheme(4.2)can be explained as a Fourier series,since the exact solution is a polynomial function,during the procedure of computing the regularization solution,the node numberMshould be chosen as a larger number relatively,here we takeM=50,and according to the numerical results in[18,19],the truncated term numbermhas no necessity to be taken too big,the best value should be 5 or 6,here we take it as 5. We use a regularization method to solve a Cauchy problem of nonlinear elliptic equation.The existence,uniqueness and stability of the regularization solution are proven,under apriori bound assumptions for the exact solution,the convergence estimates for 0 Table 1 The relative root mean square errors (u)for various noisy levels. Table 1 The relative root mean square errors (u)for various noisy levels. ε 0.0001 0.001 0.01 0.1 p=1 0.0097 0.0099 0.0114 0.0252 p=2 0.0098 0.0102 0.0150 0.0563 p=3 0.0097 0.0100 0.0115 0.0253 Figure 1 y=0.4,ε=0.01. Figure 2 y=1,ε=0.01.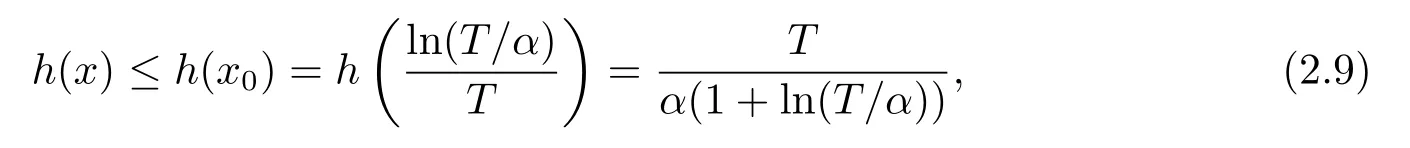
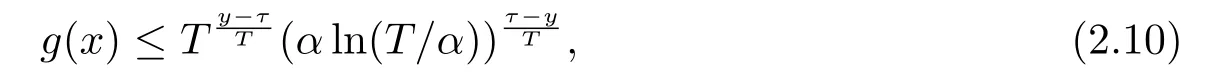
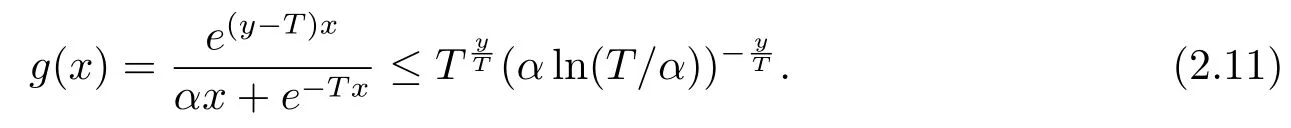
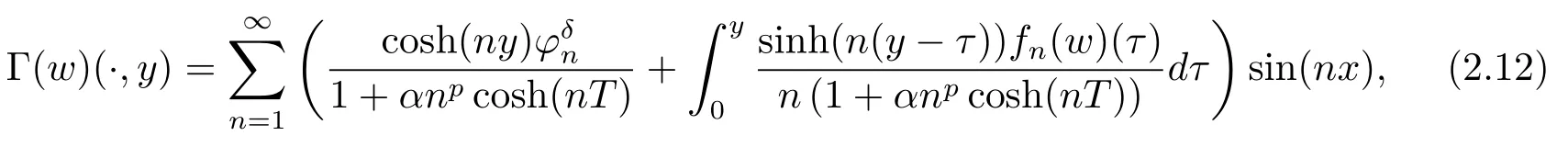
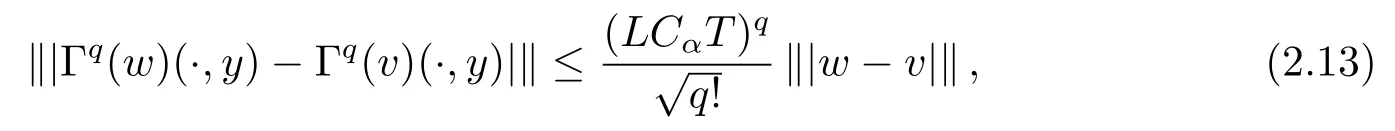
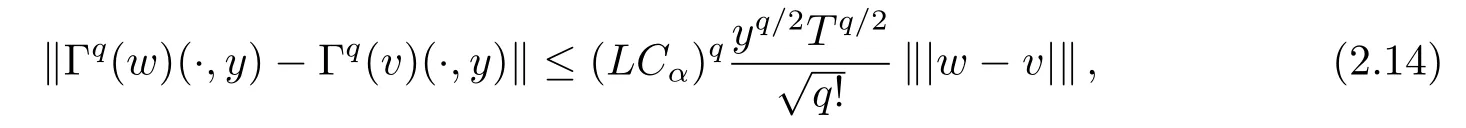

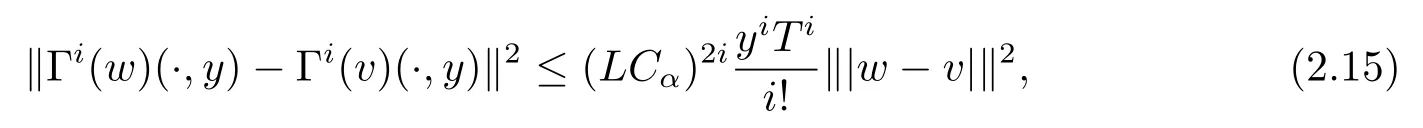
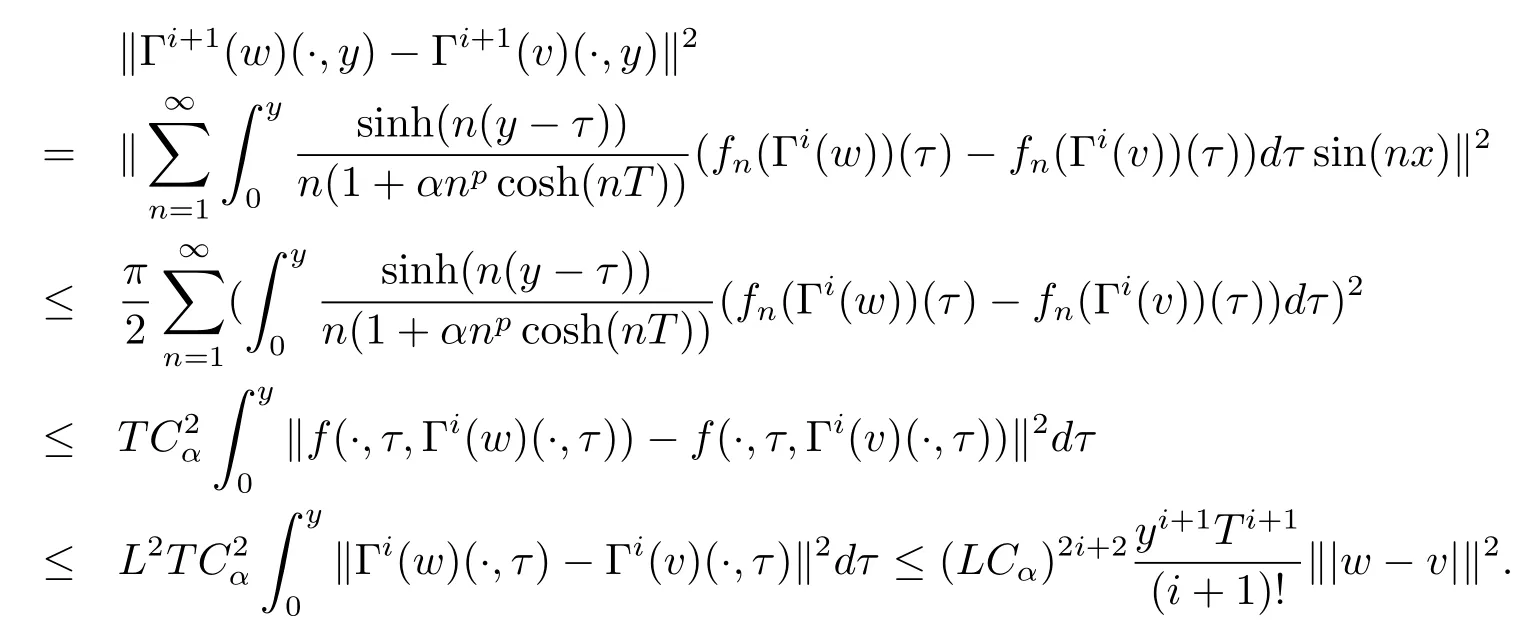

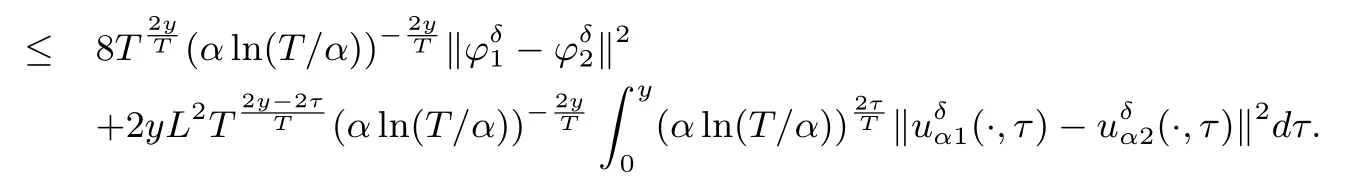
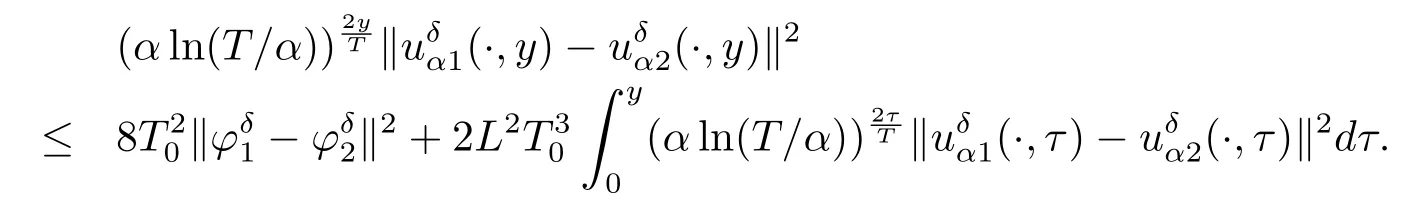
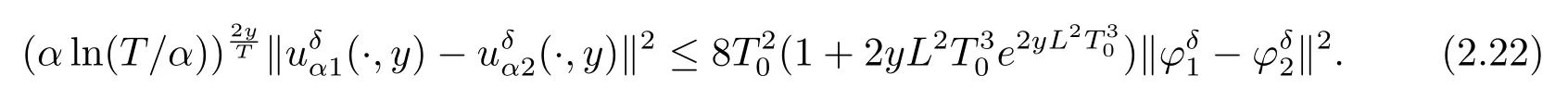
3 Convergence Estimate
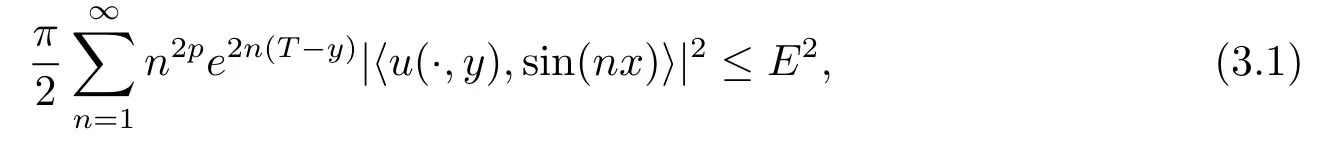

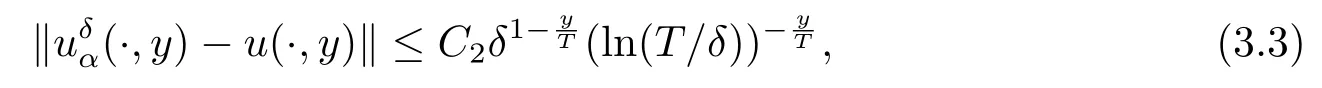
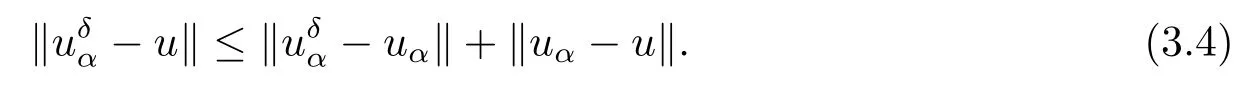
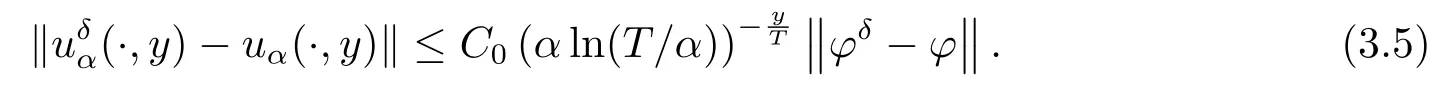
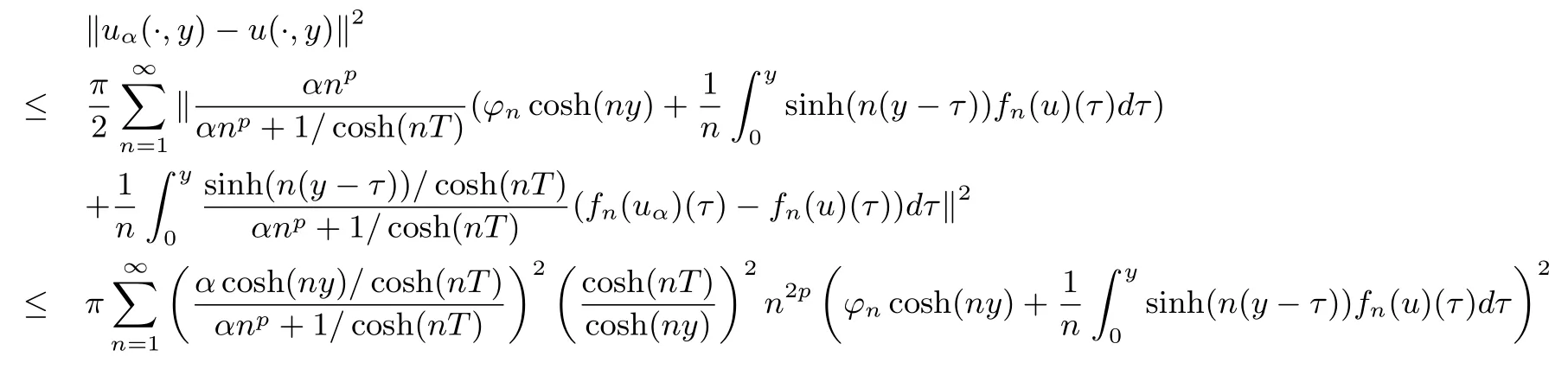

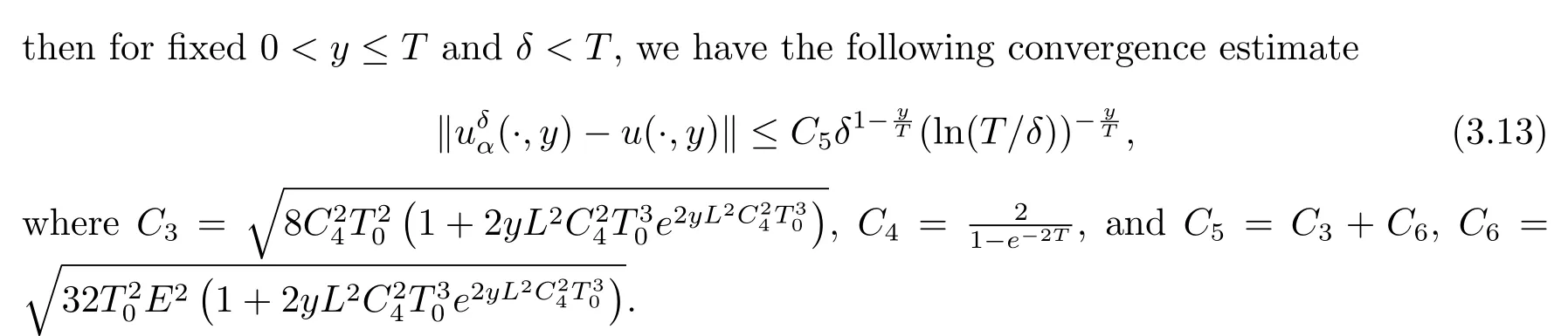
4 Numerical Experiments
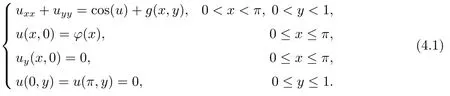
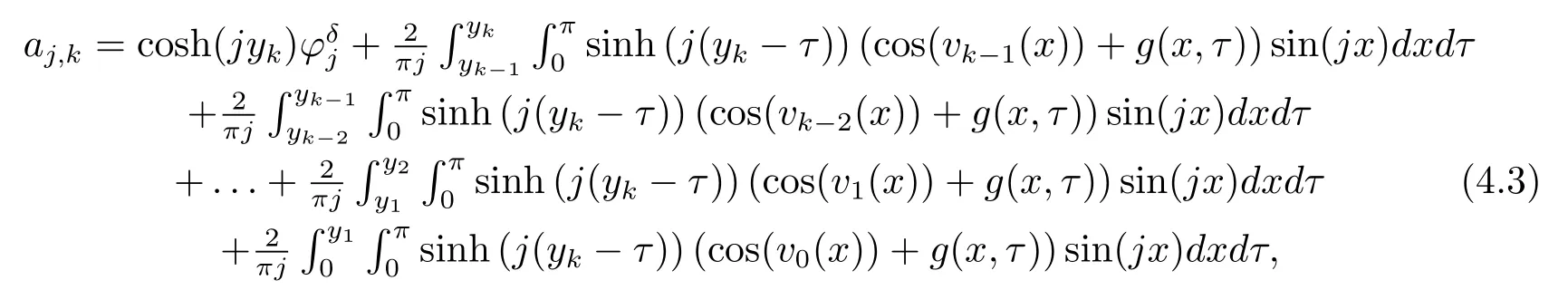
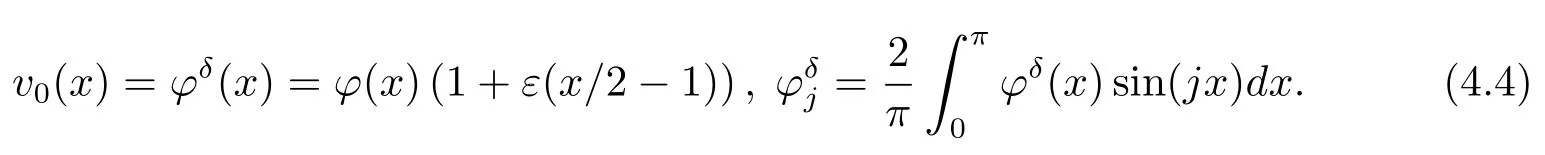
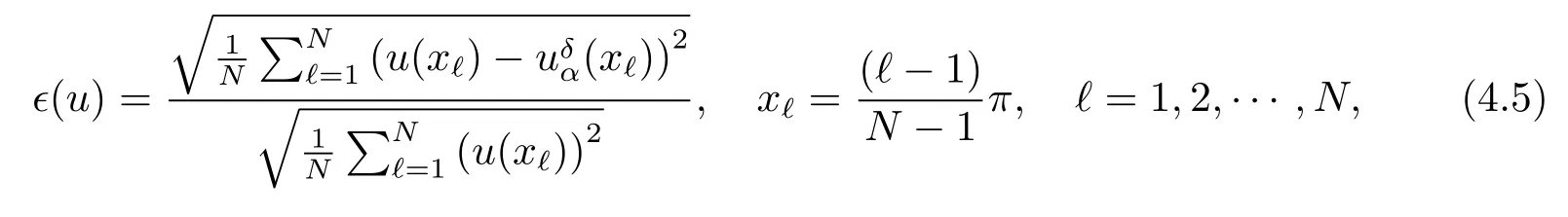
5 Conclusions