LIE-TROTTER FORMULA FOR THE HADAMARD PRODUCT *
Jing WANG (王靜) ?
School of Information, Beijing Wuzi University, Beijing 101149, China E-mail: wangjingzzumath@163.com
Yonggang LI (李永剛)
College of Science, Zhengzhou University of Aeronautics, Zhengzhou 450015, China E-mail: liyonggang914@126.com
Huafei SUN (孫華飛)
School of Mathematics and Statistics, Beijing Institute of Technology, Beijing 100081, China Beijing Key Laboratory on MCAACI, Beijing 100081, China E-mail: huafeisun@bit.edu.cn
Abstract Suppose that A and B are two positive-definite matrices, then, the limit of (Ap/2BpAp/2)1/p as p tends to 0 can be obtained by the well known Lie-Trotter formula. In this article, we generalize the usual product of matrices to the Hadamard product denoted as ? which is commutative, and obtain the explicit formula of the limit (Ap? Bp)1/p as p tends to 0. Furthermore, the existence of the limit of (Ap? Bp)1/p as p tends to +∞ is proved.
Key words Lie-Trotter formula; reciprocal Lie-Trotter formula; Hadamard product; positive-definite matrix
1 Introduction
Let M(n,C) denote the space of all n×n matrices with complex entries, H(n) denote the vector space of Hermitian n×n matrices, and H+(n) denote the set of n×n positive-definite matrices. For X, Y ∈ M(n,C), the well-known Lie-Trotter formula, as originally established in [1, 2], is
The Lie-Trotter formula can easily be modified to symmetric form ([3]), especially, when restricted to matrices A, B ∈H+(n), the formula (1.1) can be rephrased as

A similar formula holds for the limit of(Ap?Bp)2/pas p tends to 0,where A?B is the geometric mean of A and B ([4]). In [5, 6], the authors considered the explicit formula of the limit of(Ap/2BpAp/2)1/pas p tends to+∞, which is called the reciprocal Lie-Trotter formula,and this formula can be obtained by the log-majorization relation ([7]).
It is known that for any two positive-definite matrices A, B, the Hadamard product of A and B denoted by A ?B is also a positive-definite matrix ([8]). For A, B ∈H+(n), T. Ando settled affirmatively the conjecture of Johnson and Bapat on the Hadamard product ([9])
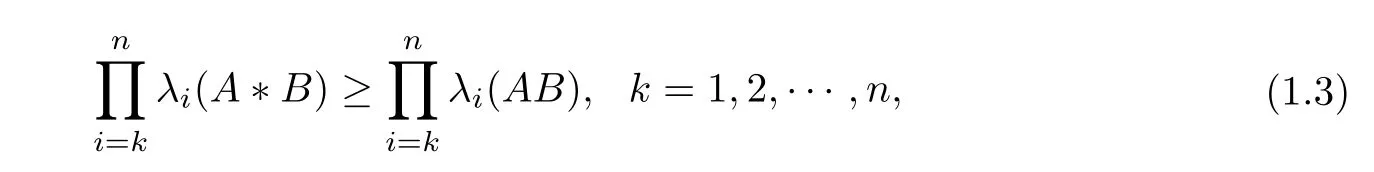
where λi(A) are the eigenvalues of A, and λ1(A) ≥λ2(A) ≥···≥λn(A). In [10], by studying the eigenvalues of(Ap?Bp)1/pfor p ∈(0,1],G.Visick presented a number of intervening terms for inequality (1.3). Besides, to progress further on the Lie-Trotter formula (1.2), we find that the limit of (Ap?Bp)1/pas p tends to 0 is related to formula (1.2). That is, according to the latter case for the Hadamard product, the Lie-Trotter formula can be derived. Within this motivation, we investigate the Lie-Trotter problem that the limit of (Ap?Bp)1/pas p →0 for positive-definite matrices A and B, as well as the reciprocal Lie-Trotter problem. It is interesting that the explicit Lie-Trotter formula for the Hadamard product is obtained,and the existence of the reciprocal Lie-Trotter formula for the Hadamard product is proved.
The remainder of the article is organized as follows. In Section 2,we review the fundamental notions and definitions, and show some important conclusions of operator-monotone function.The Lie-Trotter formula for the Hadamard product is obtained in Section 3. In Section 4, we prove the existence of the reciprocal Lie-Trotter formula for the Hadamard product.
2 Preliminaries
In this section, we recall some notions and definitions from matrix analysis, and introduce some important results of the operator-monotone function, which are used through the article(refer to [11–15]).
Let Cnbe the n-dimensional complex vector space with the inner product

where x,y ∈Cn, and superscript xHdenotes the conjugated transpose of x.
We say A ∈H(n) is positive-semidefinite, that is, A ≥0, if A satisfies
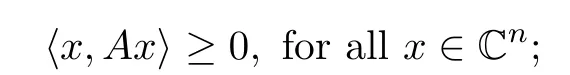
and positive-definite, that is, A>0, if
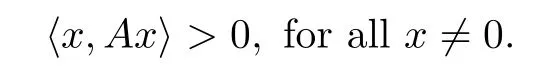
We denote that A ≥B, B ∈H(n), if
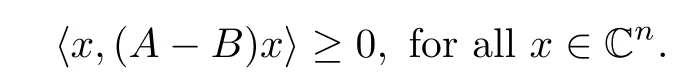
2.1 The Hadamard product and the tensor product
For any two matrices A=(aij), B =(bij) in M(n,C), the Hadamard product (also known as the Schur product or the entrywise product) A ?B is defined as ([16, 17])
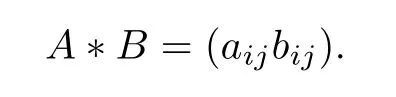
It is noticed that the Hadamard product is different from the usual matrix product, and the most important is the commutativity of Hadamard multiplication, that is, A ?B =B ?A.
An important way of putting matrices together is to construct their tensor product (sometimes called the Kronecker product). If A, B ∈M(n,C), then, their tensor product is defined as
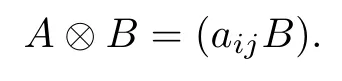
The matrix A ?B is an n2-square matrix. The following formulas for tensor product are well known ([18])

In [19, 20], the authors showed that the Hadamard product is a principal submatrix of the tensor product, and the main result can be summarized as follows.
Lemma 2.1For any A, B ∈M(n,C), then,

where Q?= [E11,··· ,Enn], and the n×n matrices Eiifor i = 1,··· ,n have a 1 in position(i,i) and zeros elsewhere.
Remark 2.2The n2×n matrix Q satisfies the property Q?Q=I,where I is an n-square identity matrix.
2.2 The operator-monotone function
The operator-monotone function is a generalization of the real-valued function, and the special case is the matrix monotone function. For A ∈H+(n), using the spectral theorem, we have ([21])
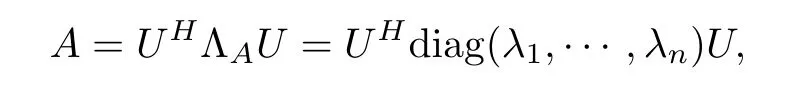
where U is a unitary matrix.
For the function f(x) (x ∈(0,+∞)), we define the matrix function as
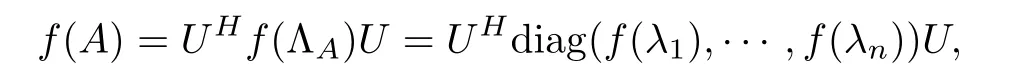
where the operator-monotone function satisfies that
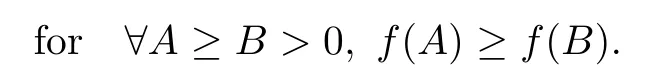
In 1933,K.L?wner successfully characterized the operator monotonicity in term of positive semi-definiteness of the so-called L?wner matrices. A part of the deep theory of L?wner is summarized in the following lemma. A complete account of L?wner’s theory can be found in the book [22].
Lemma 2.3The following statements are equivalent for a real-valued continuous function f on (0,+∞):
(i) f is operator-monotone;
(ii) fadmits an analytic continuation to the whole domain Im z≠0 in such a way that Im f(z)·Im z ≥0;
(iii) f admits an integral representation
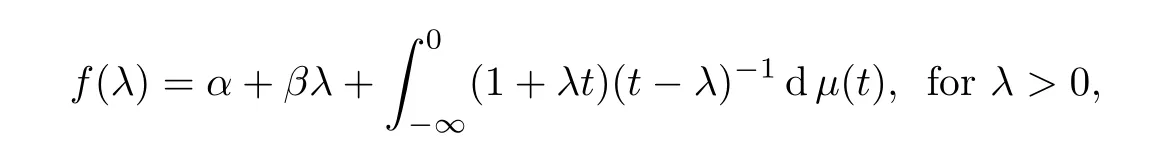
where α is a real number,β is a non-negative real number,and dμ(t)is a finite positive measure on (?∞,0].
According to L?wner’s theory, T. Ando gave a characterization for the operator-monotone function associated with the normalized positive linear map in [23].
Lemma 2.4If a function f is operator-monotone on (0,+∞), then, the map A →f(A)is concave on H+(n). And if Φ is a normalized positive linear map on H(n), then, for any A ∈H+(n)
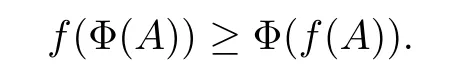
3 Lie-Trotter Formula for the Hadamard Product
This section aims at investigating the Lie-Trotter problem for the Hadamard product, and finding the explicit expression. At the same time, the proving method is applied to derived the well-known Lie-Trotter formula.
3.1 Limit of (Ap ?Bp)1/p as p →0
At first, we prove the following lemma.
Lemma 3.1If A, B ∈H+(n) and p ∈(0,+∞), then, the following result holds
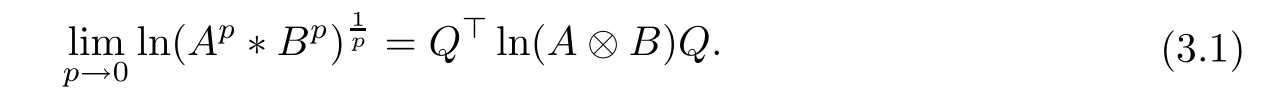
ProofAccording to (2.1) and (2.2), we have
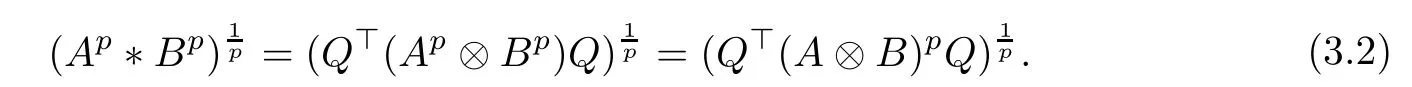
From now on, we will prove
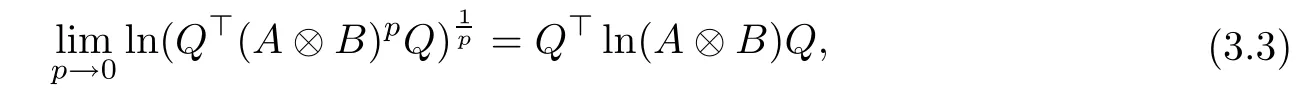
that is, for the Frobenius norm,
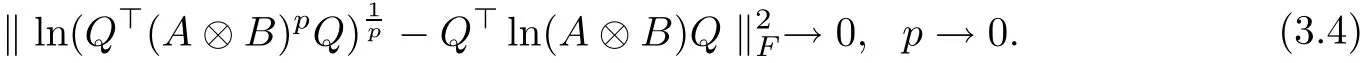
As (A ?B)H=AH?BH=A ?B, we have
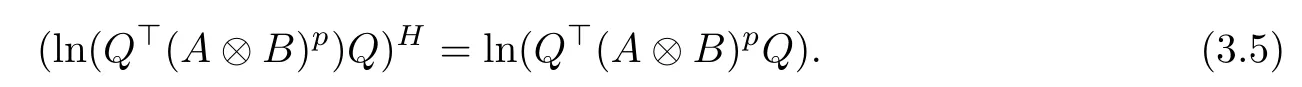
From the fact that Q?Q=I, we have
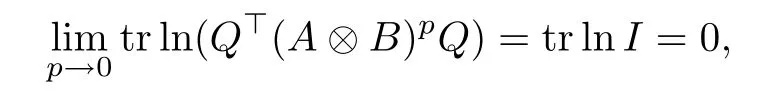
and
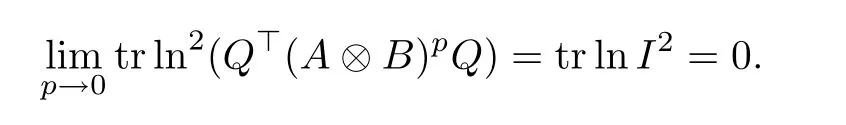
Noticing that the functions tr ln(Q?(A ?B)pQ), and tr ln2(Q?(A ?B)pQ) are continuously differentiable with respect to p, using the L′H?ospital’s rule, we obtain
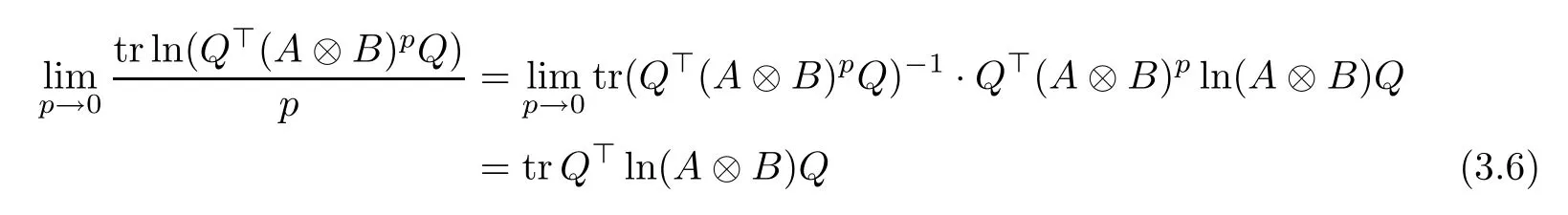
and
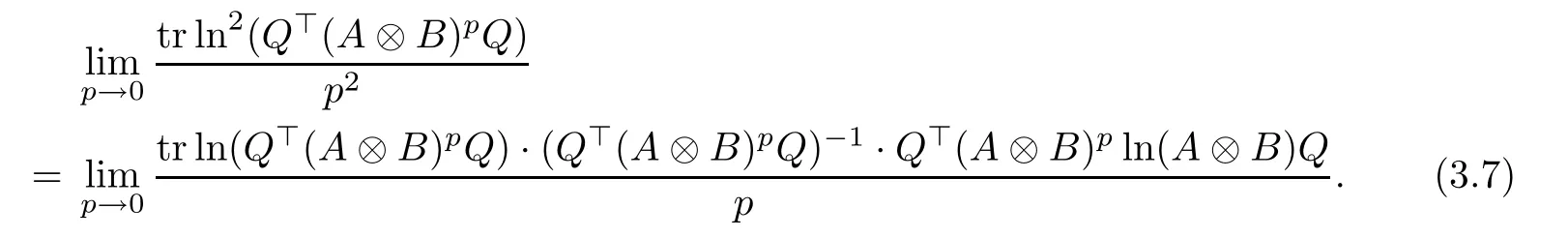
Let g(p) = tr ln(Q?(A ?B)pQ)· (Q?(A ?B)pQ)?1· Q?(A ?B)pln(A ?B)Q. As g(p) is continuously differentiable and
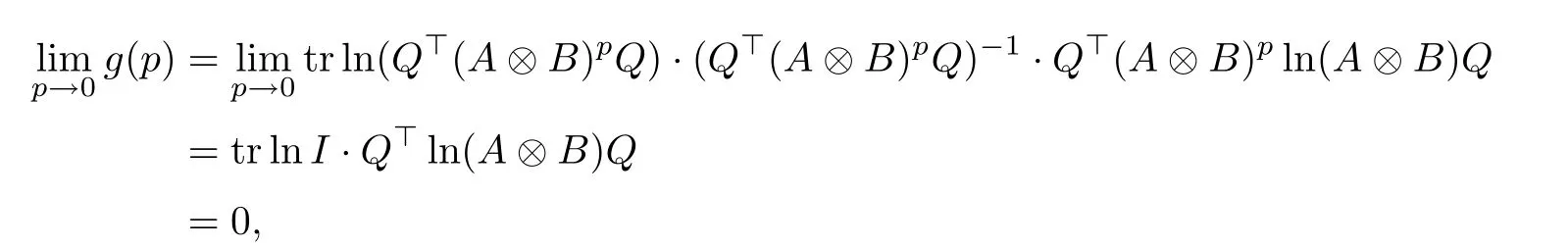
equality (3.7) can be recast as
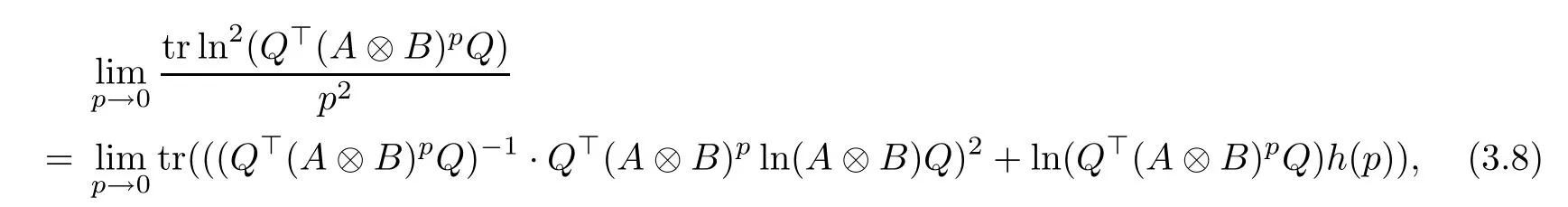
where
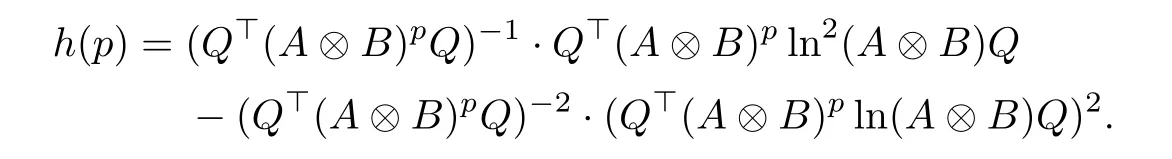
Furthermore, we have

where
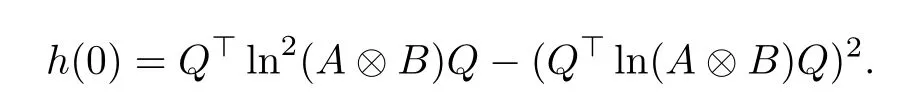
Thus, according to (3.5), (3.6), and (3.9), we have
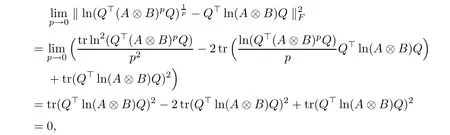
which verifies conclusion (3.4). Therefore, (3.1) can be obtained from (3.2) and (3.3).
The main result of this article is the next theorem showing the Lie-Trotter formula for the Hadamard product.
Theorem 3.2If A, B ∈H+(n) and p ∈(0,+∞), then, the following result holds
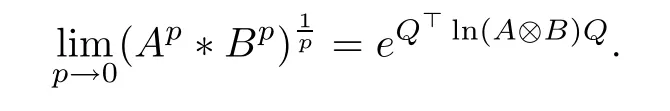
ProofAccording to Lemma 3.1,and noticing that the exponential function is continuous,we have
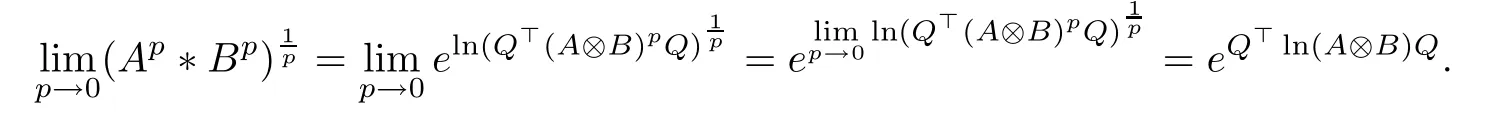
This completes the proof of Theorem 3.2.
According to Theorem 3.2, we can obtain the following corollary.
Corollary 3.3If A1,A2,··· ,Am∈H+(n)(m ≥2)and p ∈(0,+∞),the following result holds,
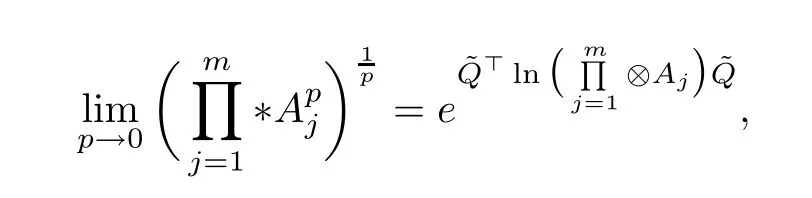

3.2 Application
Note that A, B >0,
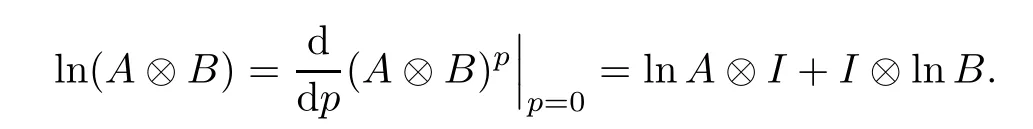
The Lie-Trotter formula for the Hadamard product can be rewritten as
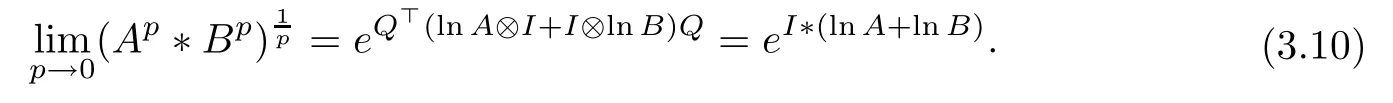
The result (3.10) has been studied to present some intervening terms for the log-majorization relation (1.3) as follows (see [10])
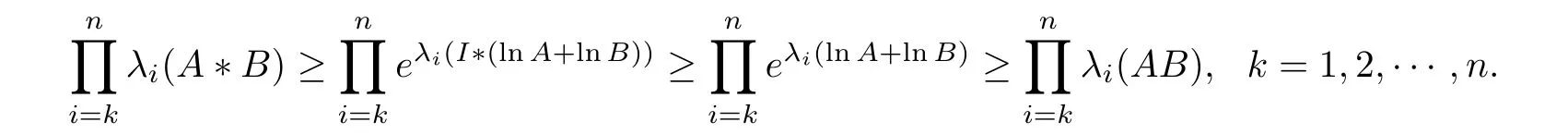
In the following part, we provide a link between Theorem 3.2 and the Lie-Trotter formula(1.2).
Let A, B ∈H+(n). By using the spectral decomposition, we have
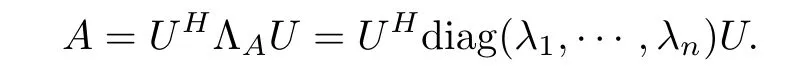
Thus,
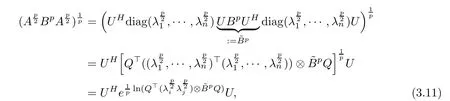
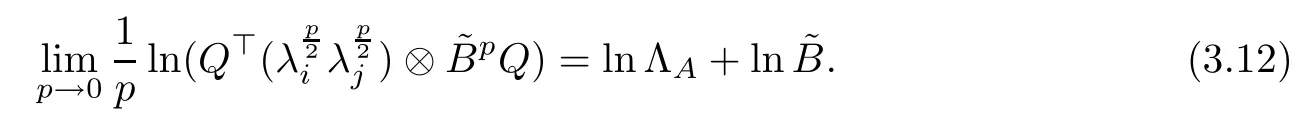
In fact, by calculations, we have
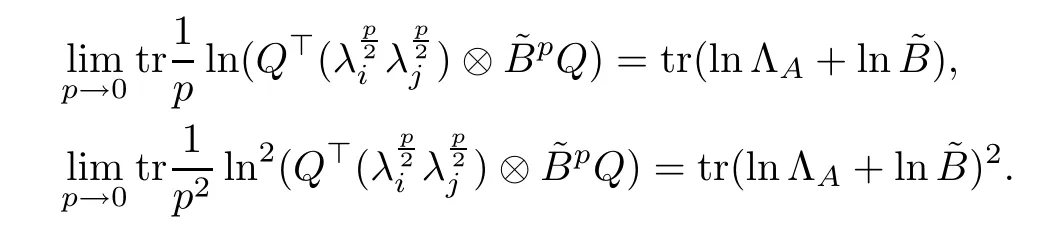
Furthermore,
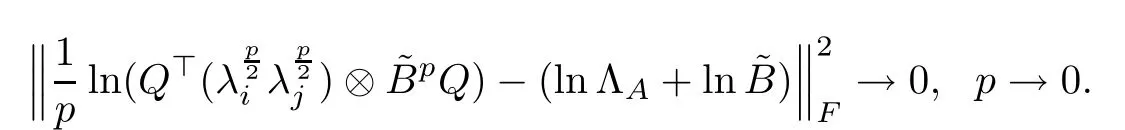
According to (3.12), (3.11) is recast as
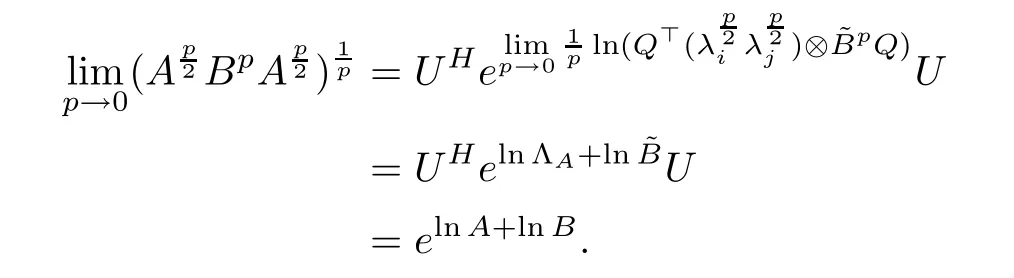
4 Reciprocal Lie-Trotter Formula for the Hadamard Product
In this section, we will prove the existence of the reciprocal Lie-Trotter formula for the Hadamard product. For A,B ∈H+(n), using the spectral theorem, we have
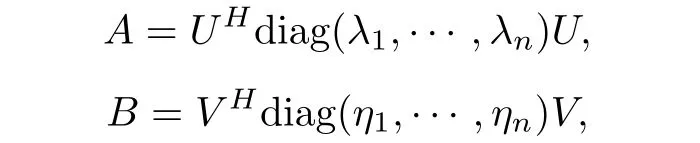
where U = (uij) and V = (vij) are unitary matrices. Firstly, we show that the limit of(Ap?Bp)1/pas p →+∞exists for the special case that A and B are diagonal matrices of H+(n), that is
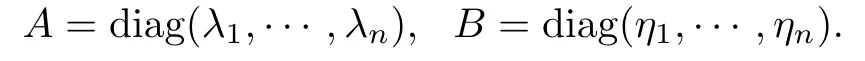
In fact, noticing that
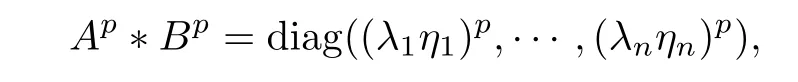
we have
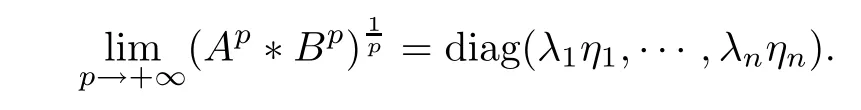
If A and B are any positive-definite matrices,we have not obtained the accurate expression of the limit (Ap?Bp)1/pas p tends to +∞. However, the following result gives the existence of the reciprocal Lie-Trotter formula for the Hadamard product.
Theorem 4.1If A,B ∈H+(n) and p ∈(0,+∞), then, the following limit exists

ProofLetBecause the mapis a normalized positive linear map, we have

which shows that Q?is operator-monotone. By Lemma 2.4, for the operator-monotone map f :, p ∈(1,+∞), we have

We can verify that (Q?Q)1/pis monotonically increasing with respect to p ∈(1,+∞). In fact, let(s ∈(1,+∞)), then, (4.3) can be rewritten as

Furthermore, we have
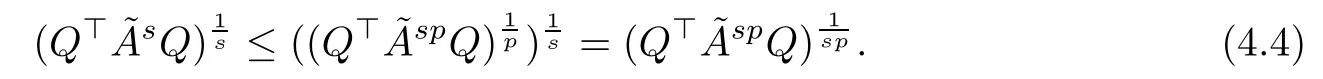
As

and Ap≤(A)I, Bp≤(B)I for any p ∈(0,+∞), according to (4.2) and (4.5), we can obtain
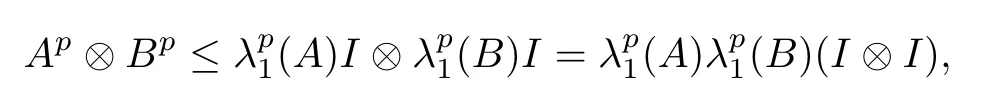
and
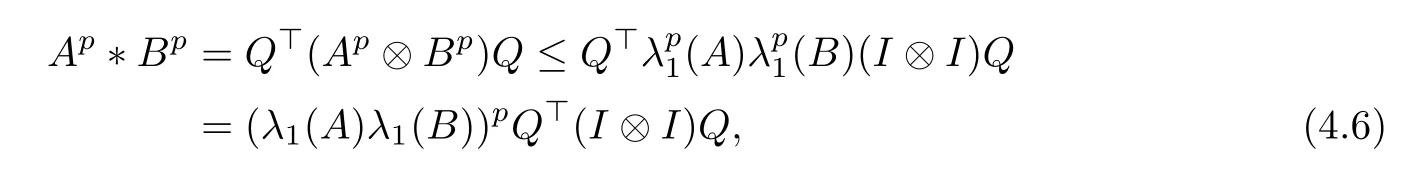
where λ1(A) and λ1(B) are the maximum eigenvalues of A and B, respectively.
Consequently, for p ∈(1,+∞), from (4.6), we have
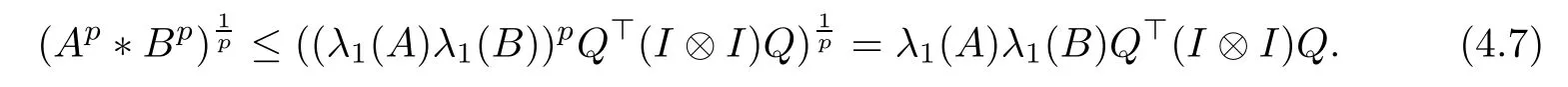
From now on, we will prove the existence of the following limit

In fact, we denote the following Schatten 1-norm as
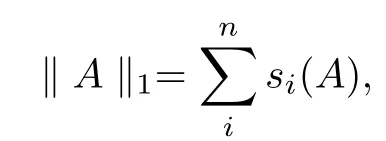
where si(A) (i = 1,··· ,n) are the singular values of A, and s1(A) ≥s2(A) ≥··· ≥sn(A),especially, for A ∈H+(n),
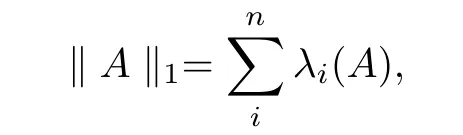
where λi(A) are the eigenvalues of A, and λ1(A)≥λ2(A)≥···≥λn(A).
Because (Q?(A ?B)pQ)1/pfor p ∈(1,+∞) is monotonically increasing, that is, for 1 Notice that if A ≤B, then, tr A ≤tr B. Thus, according to (4.9), we have that is, ?ε>0, ?N >0, when P1,P2>N, then, Therefore, we have where the first equality in (4.11)holds because (Q?(A ?B)pQ)1/pis an operator-monotone for p ∈(1,+∞). This verifies conclusion (4.8). From formula (3.2), we finishe the proof of the existence of (4.1). From the proof of Theorem 4.1, we can obtain the following corollaries. Corollary 4.2If A1,A2,··· ,Am∈H+(n) (m ≥2) and p ∈(0,+∞), then, the following limit exists Corollary 4.3If A1,A2,··· ,Am∈H+(n) (m ≥2), then, the following inequality of the H?lder type holds In this article,we can not give the explicit expression of the reciprocal Lie-Trotter formula,but we can obtain the first eigenvalue of the reciprocal Lie-Trotter formula for the Hadamard product (refer to [6]). Proposition 4.4If A, B ∈H+(n), then, the first eigenvalue of the following limit ProofLetBy the definition of matrix function, we have On the one hand, we have thus, On the other hand, noting that we have According to (4.12) and (4.13), we have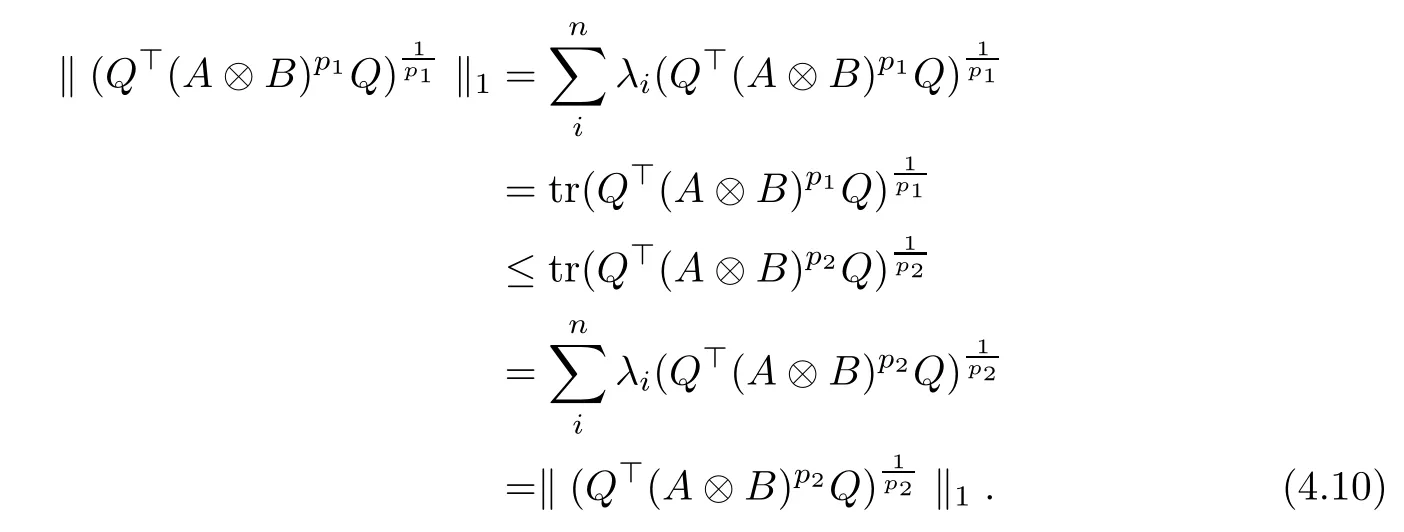
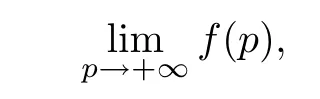
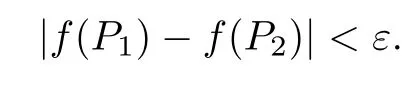

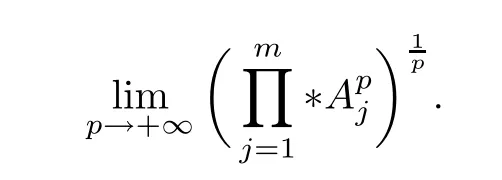
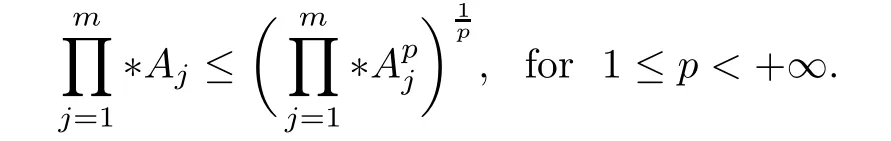
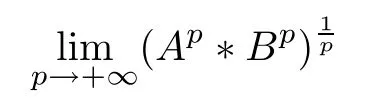
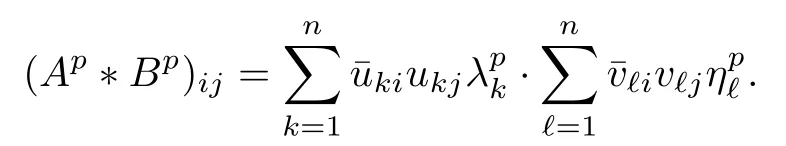
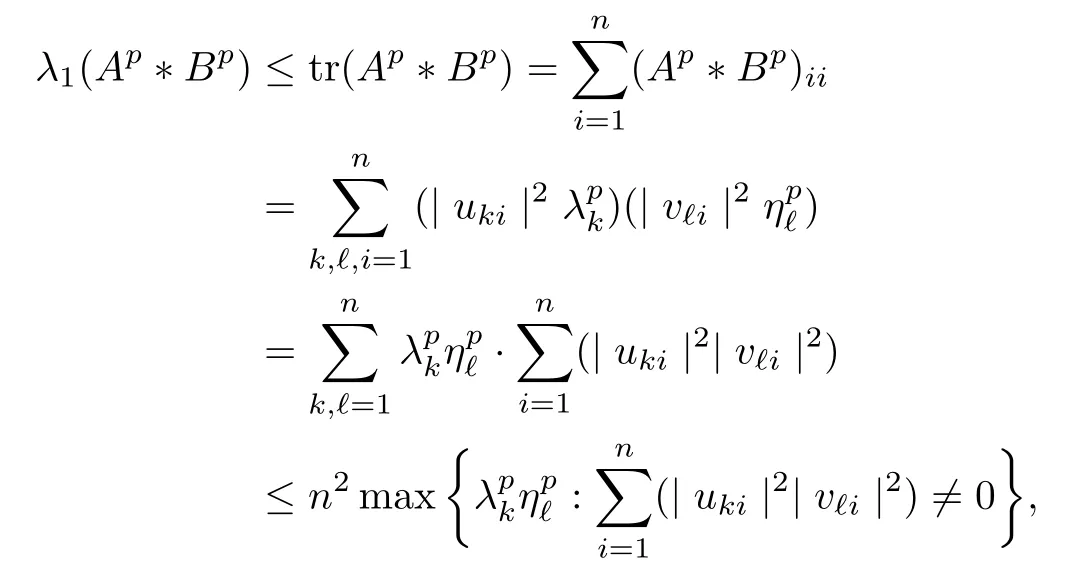
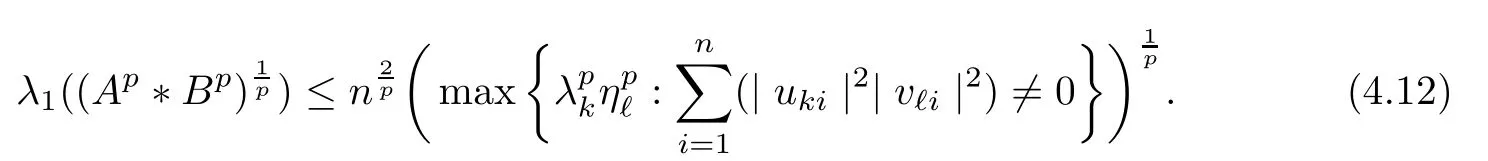

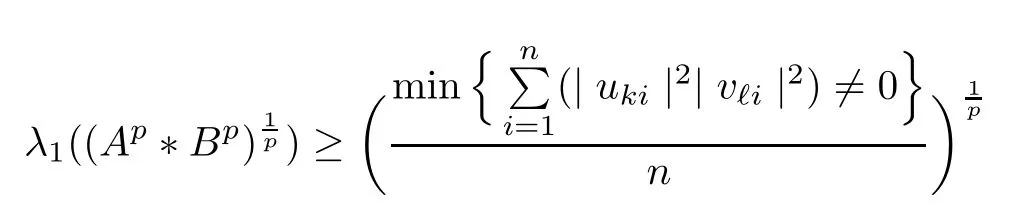

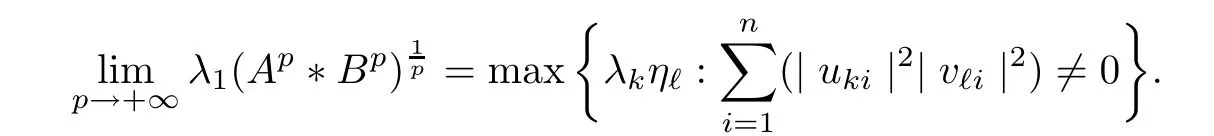
 Acta Mathematica Scientia(English Series)2020年3期
Acta Mathematica Scientia(English Series)2020年3期
- Acta Mathematica Scientia(English Series)的其它文章
- A VIEWPOINT TO MEASURE OF NON-COMPACTNESS OF OPERATORS IN BANACH SPACES ?
- MINIMAL PERIOD SYMMETRIC SOLUTIONS FOR SOME HAMILTONIAN SYSTEMS VIA THE NEHARI MANIFOLD METHOD?
- TOEPLITZ OPERATORS WITH POSITIVE OPERATOR-VALUED SYMBOLS ON VECTOR-VALUED GENERALIZED FOCK SPACES ?
- AN ABLOWITZ-LADIK INTEGRABLE LATTICE HIERARCHY WITH MULTIPLE POTENTIALS *
- MULTIPLICITY OF POSITIVE SOLUTIONS FOR A NONLOCAL ELLIPTIC PROBLEM INVOLVING CRITICAL SOBOLEV-HARDY EXPONENTS AND CONCAVE-CONVEX NONLINEARITIES *
- ASYMPTOTIC CONVERGENCE OF A GENERALIZED NON-NEWTONIAN FLUID WITH TRESCA BOUNDARY CONDITIONS?
