龔薇,王戰(zhàn)平

(寧夏大學(xué)數(shù)學(xué)統(tǒng)計(jì)學(xué)院,寧夏 銀川750021)

1.引言

隨著環(huán)境污染日益嚴(yán)重,種群的生存面臨著極大威脅.因此,我們需要建立模型去解決污染環(huán)境中的問題.然而,大量的生態(tài)學(xué)研究表明,個(gè)體尺度結(jié)構(gòu)差異要比年齡結(jié)構(gòu)對種群的發(fā)展具有更為重要的影響.鑒于種群的生存環(huán)境經(jīng)常會經(jīng)歷如季節(jié)影響等周期性變化,這樣的外部環(huán)境對資源開發(fā)具有很大的影響.由此,研究污染環(huán)境中具有個(gè)體尺度周期種群系統(tǒng)的最優(yōu)控制問題就有了非常重要的現(xiàn)實(shí)意義.

近些年,關(guān)于年齡結(jié)構(gòu)的種群模型的行為分析和控制問題有大量的研究成果.1998年,Anita等研究了周期環(huán)境中線性種群模型的最優(yōu)收獲問題,主要關(guān)注收獲總量[1],接著又研究了與年齡相關(guān)的種群動(dòng)力系統(tǒng)的最優(yōu)收獲[2].2002年,陳仁昭等人[3]研究具有空間擴(kuò)散的種群系統(tǒng)解的存在唯一性及邊界控制.2005年,付軍等人[4]研究了年齡相關(guān)的種群空間擴(kuò)散系統(tǒng)的廣義解及收獲控制.同年,雒志學(xué)和王綿森[5]研究了一類具有年齡結(jié)構(gòu)的線性周期種群動(dòng)力系統(tǒng)的最優(yōu)收獲控制問題,主要關(guān)注總的經(jīng)濟(jì)效益.2006年,何澤榮[6]研究了具有年齡結(jié)構(gòu)競爭種群的最優(yōu)收獲.Hritonenko,Yatsenko[7]研究了一類非線性森林資源模型的最優(yōu)開發(fā)問題,利用變分法推出了最優(yōu)性條件.2010年,何澤榮[8]又研究了具有年齡結(jié)構(gòu)和約束的群落系統(tǒng)的最優(yōu)收獲.同年,孫宏雨和趙春[9]研究了具有年齡結(jié)構(gòu)兩競爭種群系統(tǒng)的適定性和最優(yōu)控制.與此同時(shí),大量的學(xué)者又將個(gè)體尺度作為研究的重點(diǎn),Eucario等人[10]研究了一類具有尺度結(jié)構(gòu)資源模型的最優(yōu)收獲問題.2008年,Kato研究了非周期環(huán)境具有尺度結(jié)構(gòu)線性種群系統(tǒng)的最優(yōu)控制[11],隨后,又研究了非線性種群系統(tǒng)的最優(yōu)控制問題[12].Gasca-Leya和Hernandez[13]討論了一類線性尺度結(jié)構(gòu)模型的最優(yōu)收獲時(shí)間,并與非結(jié)構(gòu)化模型做了對比.何澤榮等人研究了一類周期環(huán)境中具有尺度結(jié)構(gòu)的種群模型的適定性及最優(yōu)收獲問題[14],接著又提出了模擬周期環(huán)境和尺度結(jié)構(gòu)的種群系統(tǒng)的最優(yōu)收獲率問題[15].2019年,梁麗宇和雒志學(xué)[16]研究了周期環(huán)境中具有尺度結(jié)構(gòu)的捕食種群系統(tǒng)的最優(yōu)控制問題.目前,考慮個(gè)體尺度的種群模型較多,但在污染環(huán)境中具有個(gè)體尺度周期種群系統(tǒng)的最優(yōu)控制種群模型尚且沒有,而這樣建立的模型更符合實(shí)際.

本文結(jié)構(gòu)如下: 第二節(jié)提出基本模型,第三節(jié)討論解的存在唯一性,第四節(jié)用極大值原理及緊性討論控制問題的存在性,最后利用法錐技巧得到控制問題的最優(yōu)條件.

2.基本模型

本文提出并研究如下污染環(huán)境中具有尺度結(jié)構(gòu)周期種群系統(tǒng)模型：

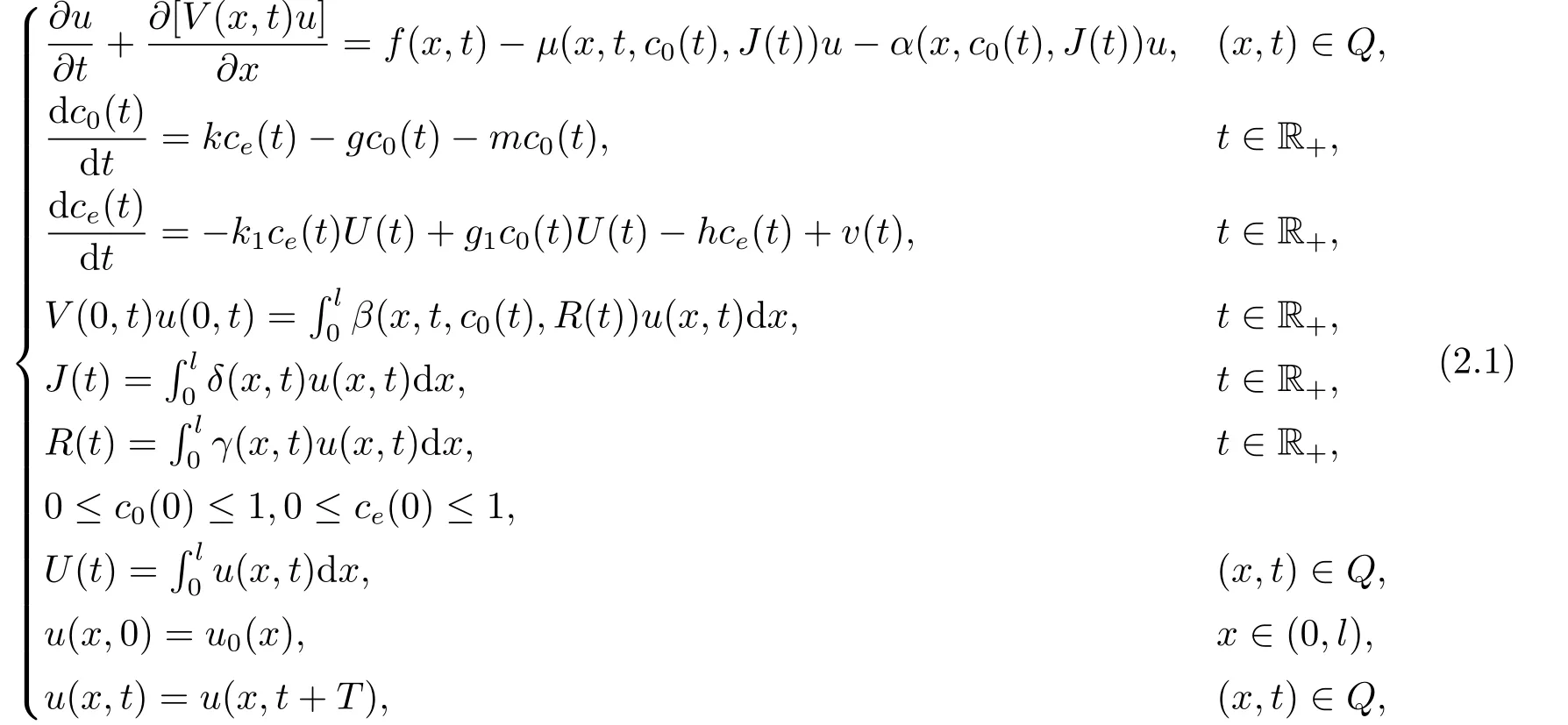
本文做以下假設(shè):

3.狀態(tài)系統(tǒng)的適定性

在本節(jié)中,不失一般性,假設(shè)α(x,c0(t),J(t))≡0,模型(2.1)變?yōu)槿缦滦问?

定義1φ(t;t0,x0)為初始條件x(t0) =x0下常微分方程x′(t) =V(x,t)的解,稱其為系統(tǒng)(2.1)通過點(diǎn)(t0,x0)的特征曲線.特別地,在x?t平面上,記通過點(diǎn)(0,0)的特征曲線為z(t).

引理1若函數(shù)u(x,t)∈L∞(Q),沿著每條特征曲線φ都絕對連續(xù),且滿足

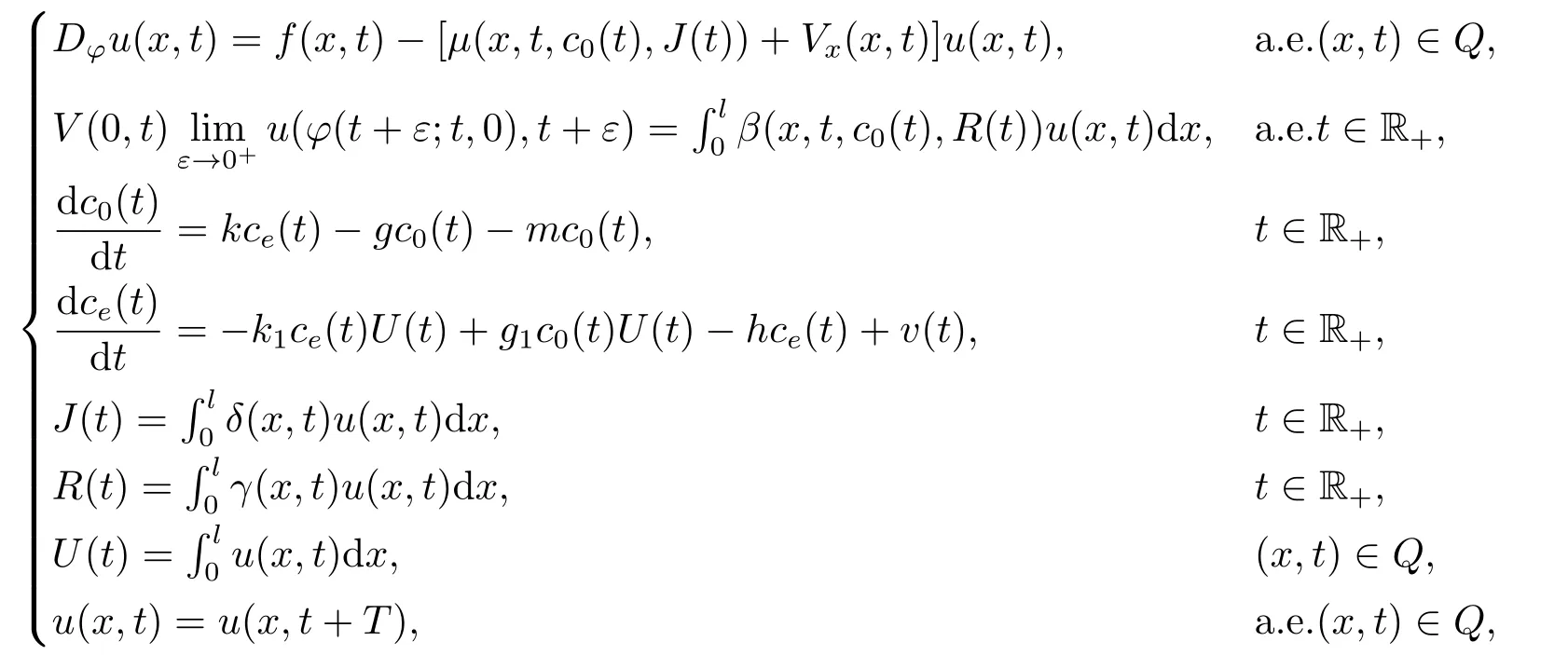
則稱(u(x,t),c0(t),ce(t))為系統(tǒng)(3.1)的解.這里Dφu(x,t)表示u(x,t)沿特征曲線φ的方向?qū)?shù),即

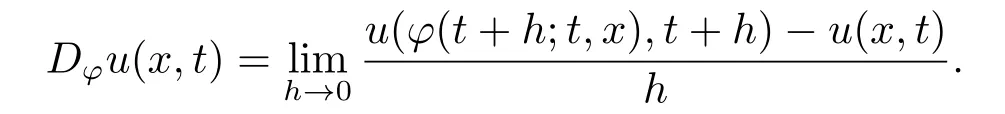
證對于x?t平面上第一象限任意固定(x,t),當(dāng)x ≤z(t),定義初始時(shí)刻τ=τ(x,t)使得φ(t;τ,0)=x.于是有φ(t;τ,x)=0.對于固定函數(shù)從而利用特征線法可知,當(dāng)x ≤z(t)時(shí)有

引理2存在正的常數(shù)F1,F2,B1,B2,使得對任意J1,J2,R1,R2∈H,t ∈(0,T),有

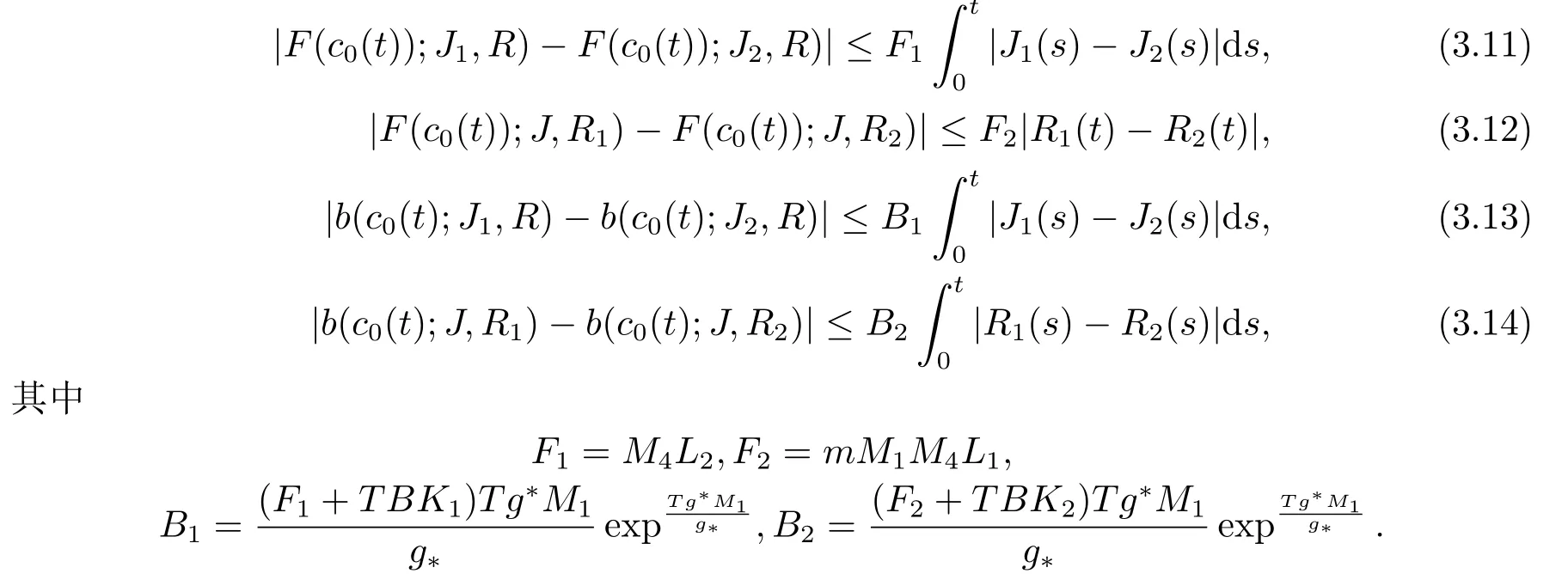
4.最優(yōu)策略的存在性

本節(jié)我們考慮下述周期環(huán)境中的最優(yōu)收獲問題:

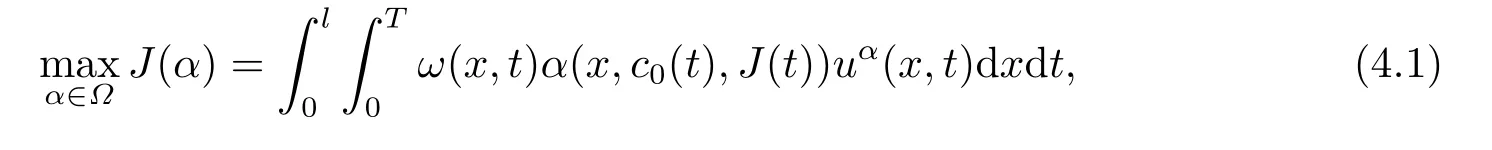
其中ω(x,t)≥0為權(quán)函數(shù),表示t時(shí)刻尺度為x的個(gè)體的經(jīng)濟(jì)價(jià)值.記uα(x,t)為給定α ∈?時(shí)控制系統(tǒng)(2.1)的解,因此J(α)表示在種群演變的一個(gè)周期內(nèi)人類開發(fā)資源所獲得的總經(jīng)濟(jì)效益.

定理4控制問題(2.1),(4.1)至少存在一個(gè)最優(yōu)解.

證令由定理3中3)可知,

其中M為權(quán)函數(shù)ω(x,t)的上界.

另一方面

5.最優(yōu)策略的結(jié)構(gòu)

其中

證因?yàn)槭强刂茊栴}(2.1)的最優(yōu)對,對于任意固定的ν ∈T?(α?),以及充分小的ε>0時(shí),有αε:=α?+εν ∈?,由J(α?)為J(α)的最大值,即J(u?+ε,v?+ε)≤J(u?,v?),

可得

在(5.5)的前三式分別乘以q1,q2,q3,第一式在Q上積分,第二,第三式在上積分得以下結(jié)果:

在(5.5)的一式兩邊同時(shí)乘以q1,并在Q上積分,得