Influence of velocity on the transmission precision of the ball screw mechanism ①
Kong Deshun(孔德順)
(*Institute of Standard Metrology, China Academy of Railway Sciences Corporation Limted, Beijing 100081, P.R.China) (**Beijing Huaheng Technology Co. Ltd., Beijing 100081, P.R.China)
Abstract
Key words: ball screw mechanism (BSM), uniform motion, structural parameters, transmission precision
0 Introduction
As a key component of computer numerical control, the performance of the ball screw mechanism (BSM) has great impact on process quality. A credible BSM enables high precision manufacturing of parts, close tolerances, and improves productivity in the workplace. The parameters affecting the performance of the BSM include contact angle, helix angle, and the pitch radius of the screw, and it have been found that the running status (i.e., sliding versus rolling) between the balls and raceway can have a significant effect on transmission precision of the BSM. Refs[1,2] studied the helix motion rule of the balls in the raceways using analytical method, proved that there are both pure rolling and sliding between the balls and the raceways in the operation process of the ball screw mechanism, and developed theories for evaluating the efficiency. Refs[3-5] introduced the theory of differential geometry of curve to analyze the motion laws of a ball considering the effect of the elastic deformation of contact angle, and found that the self-spin and rotational angular velocities of the ball have an approximately linear relationship with the rotational velocity of screw. Ref.[6] affirmed the influencing rules of contact angles and helix angles of the BSM on the slide-roll ratio, and found that it had an opposite trend of the slide-roll ratio, and an increase in helix angle significantly decreased the slide-roll ratio at contact pointB. Ref.[7] established the model of the dynamic contact angle of BSM combined with the geometric parameters of the ball and the raceway between nut and screw. He verified that the inner contact angles in screw raceway are always greater than the external angles in nut raceway under high velocity working conditions. Ref.[8] found that the torque fluctuation of BSM came from the load change of the contacting balls between the nut and the screw shaft during ball circulation, and the torque fluctuation and position deviation can be decreased, as the load of the ball decreasing. Ref.[9] and Ref.[10] found 5 different motion states between the ball, the screw of raceways, and the nut of raceways by analysis and also evaluated the effects of the motion velocity of the ball on the slide-roll ratio. At the same time Kong confirmed that the existence of the slide-roll mixed motion at the ball contact pointAbetween the ball and the screw raceway and pure rolling at the ball contact pointBbetween the ball and the nut raceway during the accelerated motion. And Refs[10,11] proved that with the increase in the BSM’s contact angle, the slide-roll ratio at the contact points decreases, and the contact angle has relatively significant effect on the slide-roll ratio. In the above cases, the motion rules of the ball were explored when the BSM is under a motion and quasi-static state. However, there is no quantitative analysis on the influence of contact angle, helix angle, and the pitch radius of the screw on transmission precision. The motion characteristics of the ball during the uniform motion of the BSM decreased the wear of the BSM during this process and increased its precision and service life[12,13].
Based on Refs[9,10,14], this paper further analyzes the kinematic laws of the contact point between the ball and raceways under 4 types extreme conditions for accelerated motion and uniform motion. Through the comparison and analysis of simulation values and test values, it is verified that the slide-roll mixed motion at the ball contact pointAand pure rolling at the ball contact pointBduring the accelerated motion and uniform motion of the screw. Moreover, the effect of the screw velocity on contact angle, helix angle and the pitch radius of the screw directly affected the velocity of the nut, under the accelerated and uniform motion state of the screw, larger angular velocity of the screw resulted in an increase in the displacement deviation of the nut. These parameters of the nut are considered to improve the transmission precision of the BSM.
1 Contact angle of BSM
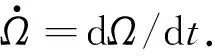
The contact angle of the BSM determines not only the relative position relationships between the balls and raceways, but also the kinematic relationship among the screw, balls, and nut. The position vectors of contact pointAbetween the ball and screw raceway and contact pointBbetween the ball and nut raceway (Fig.2) are defined using theFrenet-Serretcoordinate systemOHtnb:
(1a)
(1b)
whereβAis the contact angle between the ball and screw raceway,βBis the contact angle between the ball and nut raceway,αis the helix angle,rbis the radius of the ball, andris the circle radius of the ball center locus helix path.
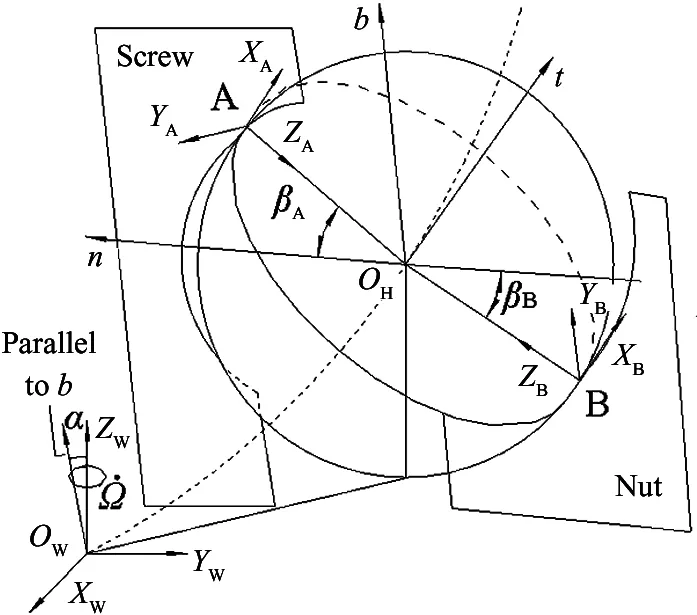
Fig.1 Three coordinate system of ball-screw
Fig.2 showsrSis the curvature radius of the screw raceway andrNis the curvature radius of the nut raceway. The arc center track of the screw raceway section intersects the normal plane of the ball center track at the pointCS. Arc center track of the nut raceway section intersects the normal plane of the ball center track at the pointcN. Ball centerOHis all in the normal plane of the ball center track.
Assuming that the velocity of the ball’s center relative to the screw in the tangential direction of the helix path isvbtand its angular velocity relative to the coordinate systemOHtnbareω=[ωbt,ωbn,ωbb], the velocity (i.e., relative sliding velocity) of contact pointsAandBon the ball relative to pointsAandBon the screw, respectively, can be expressed as follows[8,9]:
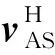
(2a)
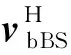
(2b)
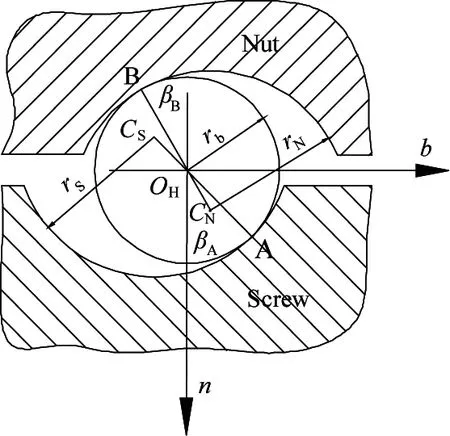
Fig.2 Contact angle
2 Kinematics of the ball contact points
During rotational motion of the screw, four extreme conditions are defined and the contact points of the ball are taken into consideration in order to conveniently analyze the uniform kinematic characteristics of the balls within the raceways.
(1) When there is pure rolling at contact pointAbetween the ball and the screw raceway and rolling-sliding mixed motion at contact pointBbetween the ball and nut raceway. The sliding velocity at contact pointAbetween the ball and the screw raceway is calculated using Eq.(3a), as well as the rolling velocity at contact pointAbetween the ball and the screw raceway using Eq.(3b) in Refs[8,9]:
(3a)
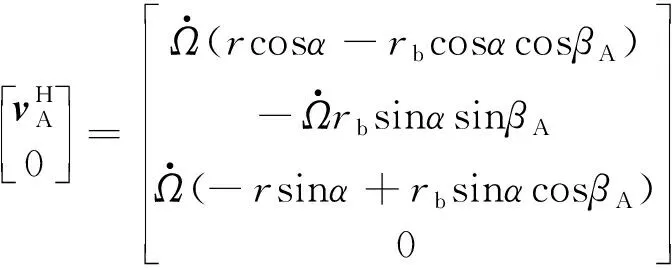
(3b)
Then, using Eq.(3a), Eq.(4) can be obtained:
(4)
By substituting Eq.(4) into Eq.(2b), the relative sliding velocity at pointBbetween the ball and nut raceway is obtained as follows:
(5)
The rolling velocity at contact pointBof the nut is equal to the rolling velocity at contact pointBof the ball minus the sliding velocity at contact pointBof the ball. By combining Eq.(3a) and Eq.(5), the rolling velocity at contact pointBof the nut is obtained as follows:
(6)
In theFrenet-Serretcoordinate systemOHtnb, the velocity of pointBon the nut relative to pointBon the screw is calculated as Eq.(7).
(7)

(8)
In the inertial coordinate systemOWXWYWZW, the velocity of nut at contact pointBcan be expressed as

(9)
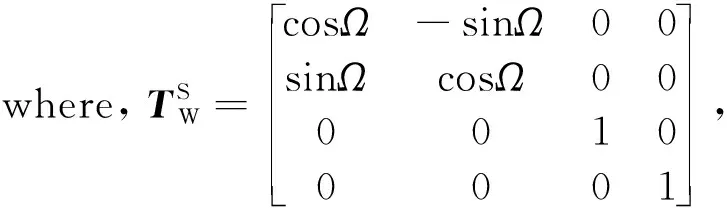
Finally, Eq.(9) is used to obtain the velocity of pointBon the nut in the inertial ordinate systemOWXWYWZWas follows:
(10)
(2) When the relative motion between the ball and screw raceway is pure sliding, i.e., there is no relative rolling at pointA, the ball and nut are fixed together. In this case, the BSM is similar to the Trapezoidal Lead Screw, and the relative velocity at pointBcan be calculated as
(11)
The relative rotational angular velocity between the balls and the screw can be defined as the relative angular velocity between the nut and the screw. So the angular velocity of the ball in theFrenet-Serretcoordinate systemOHtnbis defined as
(12)
Since the ball and the nut are motionless relative to the other, the velocity of the nut is equal to the velocity at contact pointAof the ball in the direction of screw axis. Thus, the velocity of the nut is obtained as
(13)
(3) When there is pure rolling at contact pointBbetween the ball and the nut raceway and rolling-sliding mixed motion at contact pointAbetween the ball and the screw raceway. Under these conditions, the relative sliding velocity at contact pointBbetween the ball and the nut raceway is zero, and the sliding velocity at pointBcan be expressed using Eq.(14).
(14)
Then, from Eq.(14), the following is obtained:
(15)
By substituting Eq.(15) into Eq.(2a), the relative sliding velocity at pointAis obtained as
(16)
The rolling velocity at contact pointBof the nut is equal to the rolling velocity at contact pointAof the ball minus the sliding velocity at contact pointAof the ball. By combining Eq.(3b) and Eq.(16), the rolling velocity at contact pointBof the nut is obtained as
(17)
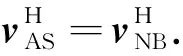
Using Eq.(17), Eq.(18) can be got:
(18)
By substituting Eq.(3b) and Eq.(7a) into Eq.(18) for simplification, the velocity of the nut is
(4) When the relative motion between the ball and nut raceway is pure sliding, i.e., there is no relative rolling at pointB. Similar to condition Eq.(2), the ball and screw are considered to be fixed together, thus the BSM is comparable to the Trapezoidal Lead Screw. The velocity of contact pointBbetween the ball and the nut raceway is similar to pure sliding at contact pointAbetween the ball and the screw raceway, and the velocity of the nut can be expressed as
(19)
3 Experimental results and comparison to the theoretical model
To verify the motion rule of the ball contact points of the BSM during the uniform motion, a test bench is established to test BSM in Fig.3, and the velocity and displacement of the nut are recorded using a laser interferometer. By substituting parameters of the BSM into Eq.(10) and Eq.(19) shown in Table 1, and get simulation data.
The velocity and displacement of the nut are recorded by the laser interferometer during the motion process of screw. And the model of the laser interferometer is RENISHAW XL80.

1 Reflector2 BSM3 Refractor4 Motor encoder5 Laser interferometer
The actual values of the nut velocities match the simulated values when the ball contact pointsAandBare under pure rolling conditions, as shown in Fig.4, and the actual values of the nut velocities are in the middle of two velocities when the ball contact pointsAandBare pure sliding. The BSM creates a centrifugal force as the screw rotates, and the normal pressure of the ball contact pointBis greater than that of pointA, therefore, the friction force of pointBis larger than that of pointAunder the same friction coefficient. Moreover, it can be concluded that the ball contact pointsAandBcannot be pure rolling at the same time in Ref.[9]. So the ball contact pointBcan be considered pure rolling while the ball contact pointApresents the rolling-sliding mixed movement.
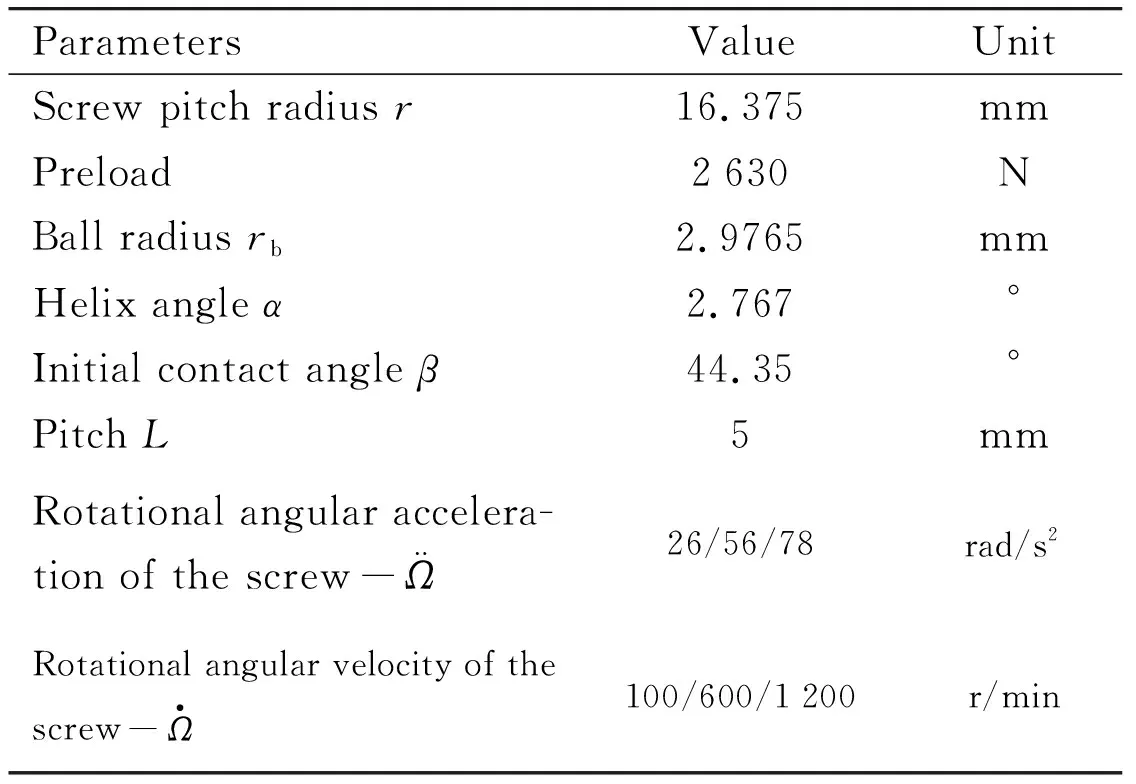
Table 1 Parameters of the BSM
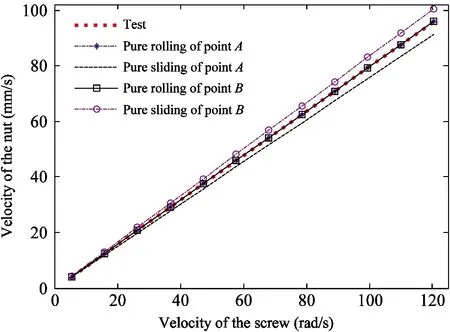
Fig.4 Relationship of screw velocity and nut velocity
4 Improving transmission precision
As the screw rotational velocity increases, the contact angle, helix angle, and ball center position relative to the screw axis position radius change in Refs[3,14]. These parameters directly affect the velocity of the nut. When the contact angle, helix angle, and the pitch radius of the screw are considered, they are affected by the screw rotation velocity. Again, the deviation values between the measured and simulated values are presented in Fig.5 and Fig.6 under the condition that the nut moves the same distance.
Under the accelerated motion state of the screw, as the nut moves the same displacement at different screw speeds, considering and ignoring the influence of the contact angle, helix angle, and the pitch radius of the screw, the deviation between the measured value and the simulated value is as follows. These variations are shown in Fig.5. The deviation values of the nut displacement reduce to 1/5 as the velocity of angular acceleration is 26 rad/s2, the displacement deviation reduces to 1/3 as the velocity of angular acceleration is 52 rad/s2, and the displacement deviation reduces to 1/1.7 relative to not considering the effects of these parameters as the velocity of angular acceleration is 78 rad/s2. Under the accelerated motion state of the screw, larger angular acceleration of the screw results in an increase in the displacement deviation of the nut.

Fig.5 The deviation values of the nut displacement at screw accelerated motion
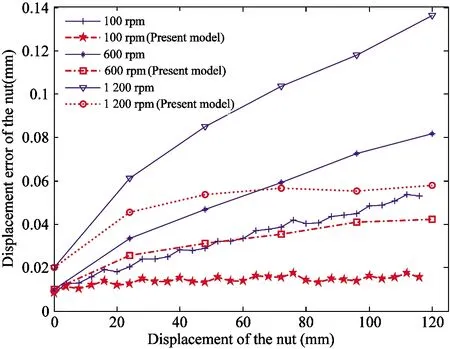
Fig.6 The deviation values of the nut displacement at screw uniform motion
Similarly, under the uniform motion state of the screw, as the nut moves the same displacement at different screw speeds, considering and ignoring the influence of the contact angle, helix angle, and the pitch radius of the screw, the deviation between the measured value and the simulated value is as follows. These variations are shown in Fig.6. The deviation values of the nut displacement reduce to 1/3.4 as the velocity of rotator is 100 rpm, the displacement deviation reduces to 1/2 as the velocity of rotator is 600 rpm, and the displacement deviation reduces to 1/1.7 relative to not considering the effects of these parameters as the velocity of rotator is 1 200 rpm. And larger velocity of the screw results in smaller values of the nut displacement deviation.
5 Conclusions
Contact angle, helix angle, and the pitch radius of the screw have significance effect on BSM transmission precision. However, these parameters have not been fully studied. As such, these parameters are chosen as the basis for the proposed kinematic model. In addition, specific operational parameters based on the existing literature are used to assess the model. The conclusions can be drawn from this study.
By empirically measuring the velocity and the displacement values using a test bench and comparing them to the simulated values, the kinematic relationships for the ball movement are verified, and the BSM parameters are optimized such that the velocity and displacement of nut are improved.
When the nut is displaced by an equal amount using different screw velocities under the accelerated motion state of the screw, the contact angle, helix angle, and the pitch radius of the screw are considered. The deviation values of the nut displacement reduce to 1/5, 1/3 and 1/1.7 relative to not considering the effects of these parameters as the velocity of angular acceleration is 26 rad/s2, 52 rad/s2and 78 rad/s2. Simultaneously, the screw velocities under a state of uniform motion, the deviation values of the nut displacement reduce to 1/3.4, 1/2 and 1/1.7 as the velocity of rotator is 100, 600 and 1 200 rpm respectively. Under the accelerated and uniform motion state of the screw, larger angular velocity of the screw results in an increase in the displacement deviation of the nut.
Finally, the effect of the screw velocity on position of nut, including contact angle, helix angle and the pitch radius of the screw, is considered to improve the transmission precision of the BSM.
 High Technology Letters2020年2期
High Technology Letters2020年2期
- High Technology Letters的其它文章
- MW-DLA: a dynamic bit width deep learning accelerator ①
- Physical layer security transmission algorithm based on cooperative beamforming in SWIPT system ①
- GNSS autonomous navigation method for HEO spacecraft ①
- Control performance and energy saving of multi-level pressure switching control system based on independent metering control ①
- Improved image captioning with subword units training and transformer ①
- RGB and LBP-texture deep nonlinearly fusion features for fabric retrieval ①
