陳 瑤

（廣州大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院,廣東廣州510000）

1951年,Fast[1]引進(jìn)了統(tǒng)計(jì)收斂的定義,稱實(shí)數(shù)序列{ xn}n≥1統(tǒng)計(jì)收斂于實(shí)數(shù)ξ,如果對(duì)任意ε ＞0,集合的漸近密度為0,即

20 世紀(jì)90 年代以來,統(tǒng)計(jì)收斂已經(jīng)成為人們研究的熱點(diǎn),它出現(xiàn)在許多領(lǐng)域,如傅里葉分析[2],三角級(jí)數(shù)[3],數(shù)論[4]和模糊數(shù)學(xué)[5]等.近年,針對(duì)序列的統(tǒng)計(jì)收斂性也提出了一些新的概念,如Baliarsingh[6]在2018年利用差分算子研究了統(tǒng)計(jì)收斂的一些新結(jié)果, 提出了分?jǐn)?shù)階差分序列的統(tǒng)計(jì)收斂性概念; ?inar[7]在2019年研究了雙序列的統(tǒng)計(jì)收斂性與雙塞薩羅可和性在乘積時(shí)間尺度上的關(guān)系,提出了雙序列在任意乘積時(shí)間尺度上的統(tǒng)計(jì)收斂性的概念.巴拿赫密度是與漸近密度密切相關(guān)的重要概念,設(shè)集合

存在,則稱它為集合A的上巴拿赫密度.引進(jìn)上巴拿赫統(tǒng)計(jì)收斂的概念,研究它與統(tǒng)計(jì)收斂的區(qū)別以及給出上巴拿赫統(tǒng)計(jì)收斂的一個(gè)必要條件.

定義1 稱實(shí)數(shù)序列{xn}n≥1上巴拿赫統(tǒng)計(jì)收斂于實(shí)數(shù)ξ,若對(duì)任意ε ＞0,集合

的上巴拿赫密度為0,即

容易驗(yàn)證上巴拿赫統(tǒng)計(jì)極限ξ是唯一存在的.由定義1,我們可以驗(yàn)證實(shí)數(shù)序列{xn}n≥1的上巴拿赫統(tǒng)計(jì)收斂性也滿足線性性,即若是一個(gè)實(shí)數(shù),則.

要證明例1,我們需要引理1.

引理1[8]當(dāng)且僅當(dāng)存在自然數(shù)集的一個(gè)嚴(yán)格單調(diào)遞增的子列,使得

E中點(diǎn)的分布如圖1所示,對(duì)任意n ∈?,存在N ∈?使得

N3+ N ＜n ≤(N + 1)3+(N + 1),

圖1 集合E的構(gòu)造Fig.1 The construction of E

再由集合E的構(gòu)造可知

即

注意到當(dāng)n →∞時(shí),N →∞.因此有

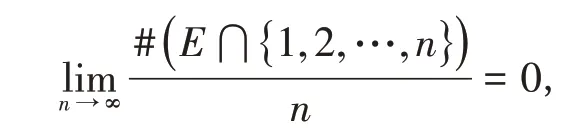
即D(E )= 0,故D(?E )= 1,由引理1可得.

以下給出上巴拿赫密度統(tǒng)計(jì)收斂的一個(gè)必要條件.

定理1 實(shí)數(shù)序列{xn}n≥1上巴拿赫統(tǒng)計(jì)收斂于實(shí)數(shù)ξ,則存在自然數(shù)集的一個(gè)嚴(yán)格單調(diào)遞增的子列

由于s的取值會(huì)隨著n的變化而變化,所以根據(jù)（2）式,存在一組正整數(shù)序列滿足

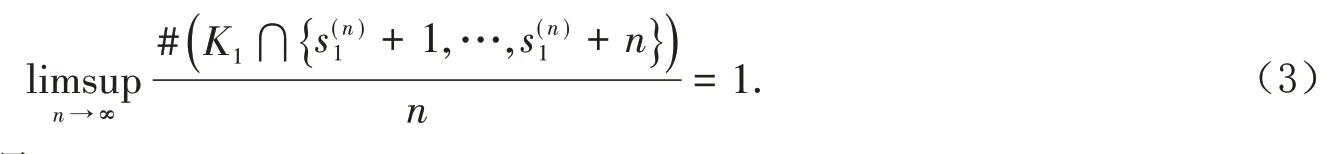
根據(jù)（3）式,存在n1∈?使得滿足

由（1）式可知,存在正整數(shù)n2≥n1滿足使得

通過歸納構(gòu)造一個(gè)單調(diào)遞增的正整數(shù)序列{nj}j≥1,當(dāng)nj+1≥nj≥nj-1時(shí)滿足和,使得

利用以上關(guān)系,我們定義子列

K的結(jié)構(gòu)如圖2所示

圖2 集合K的結(jié)構(gòu)Fig.2 The construction of K

根據(jù)（4）式,取任意nj∈?,當(dāng)nj+1≥nj≥nj-1時(shí)使得滿足