SHARP ESTIMATES FOR EIGENVALUES OF BI-DRIFTING LAPLACIAN
LI Yan-li, DU Feng
(1.School of Electronic and Information Science, Jingchu University of Technology,Jingmen 448000, China)
(2.Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062, China)
(3.School of Mathematics and Physics, Jingchu University of Technology,Jingmen 448000, China)
Abstract: In this paper, we study the four types of eigenvalue problems for the bi-drifting Laplacian.By using the weighted Reilly formula, we get some sharp lower bounds for the first nonzero eigenvalue for these eigenvalue problems on compact smooth metric measure spaces with boundary and under some condition on the m-weighted Ricci curvature, which generalize the corresponding results for the eigenvalues of biharmonic operator.
Keywords: eigenvalues; drifting Laplacian; smooth metric measure spaces; m-weighted Ricci curvature; Steklov problem.
1 Introduction
In 1977, Reilly [19]obtained a sharp lower bound for the first Dirichlet eigenvalue of the Laplacian as following.
Reilly’s TheoremLetMbe ann(≥2)-dimensional compact Riemannian manifold with Ricci curvature bounded below by (n ?1)κ> 0 and boundary.If the mean curvature of?Mis nonnegative then the first Dirichlet eigenvalue of the Laplacian ofMsatisfies
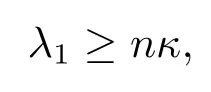
and equality holds if and onlyMis isometric to ann-dimensional Euclidean semi-sphere of radius
For the Neumann boundary case, a similar result was proven by Escobar [10]and Xia[25]independently.In [13], Li-Wei generalize these results including Dirichlet boundary and Neumann boundary to the first eigenvalue of the drifting Laplacianon compact smooth metric measure spacesisn-dimensional Riemannian manifold with a metricfis a smooth real-valued function onManddνis the Riemannian volume element related to(sometimes, we also calldνthe volume density).The drifting Laplacian is also called weighted Laplacian (or Witten Lpalacian),some interesting results concerning eigenvalues of the drifting Laplacian can be found in[7–9, 11, 13, 17, 26].Compared with Ricci curvature of the Riemannnian manifods, we can define the so-called weighted Ricci curvature Ricfon smooth metric measure spaces as following
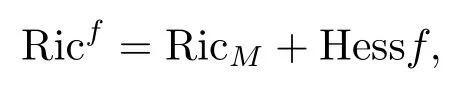
which is also called the∞-Bakrymery Ricci tensor.The equationfor some constantκis just the gradient Ricci soliton equation, which plays an important role in the study of Ricci flow.Forκ=0,κ>0,andκ<0, the gradient Ricci solitonis called steady, shrinking, and expanding, respectively.Set
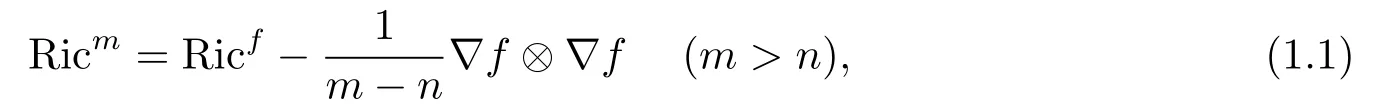
which is calledm-weighted Ricci curvature [1]ofM(also called them-Bakrymery Ricci tensor).Whenm=n,letfbe a constant and Ricm=RicM.A smooth metric measure space is not necessarily compact when Ricf ≥λ> 0, unlike in the case of Riemannian manifolds where such a complete one is compact if its Ricci curvature is bounded from below uniformly by some positive constant [21], but a interesting fact is that when Ricm ≥(m ?1)κ> 0,a complete smooth metric measure spaceis automatically compact and the diameter ofMsatisfies diam(M)
In [5], Chen-Cheng-Wang-Xia gave some lower bounds for the first eigenvalue of four kinds of eigenvalue problems of the biharmonic operator on compact manifolds with boundary and positive Ricci curvature.In[6],Du-Bezerra generalize these results to the bi-drifting Laplacian on compact manifolds with boundary and positivem-weighted Ricci curvature.Recently, Wang-Xia [24]gave some new sharp lower bounds for the first eigenvalues of the biharmonic operator on compact manifolds with boundary and positive Ricci curvature.Inspired by these investigations, in this paper, we first get.
Theorem 1.1Let (M,,,e?fdν) be ann(≥2)-dimensional smooth metric measure space with boundary?Mand denote byνthe outward unit normal vector field of?M.Assume that them-weighted Ricci curvature ofMis bounded below by (m ?1)κ>0.Letλ1be the first nonzero eigenvalue with Dirichlet boundary condition of the drifting Laplacian ofMand let Γ1be the first eigenvalue of the clamped plate problem onM,
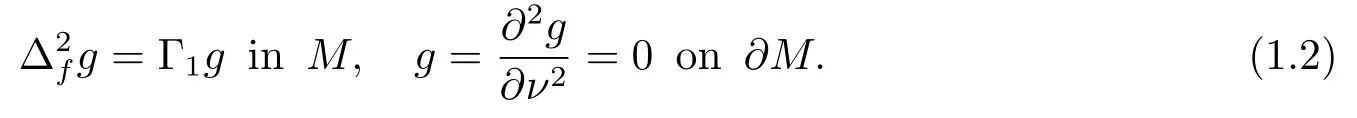
Then we have
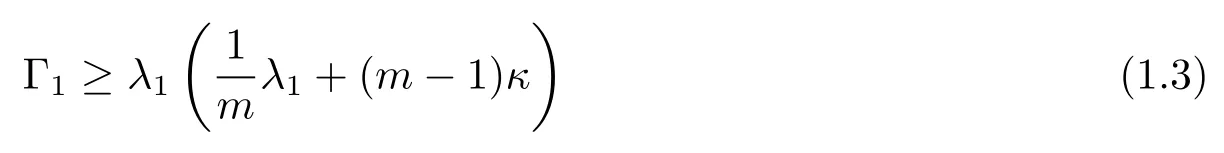
with equality holds if and only ifMis isometric to ann-dimensional euclidean unit semisphere of radius ofandfis constant.
Theorem 1.2Under the assumption of Theorem 1.2, let Λ1be the first nonzero eigenvalue of the following buckling problem
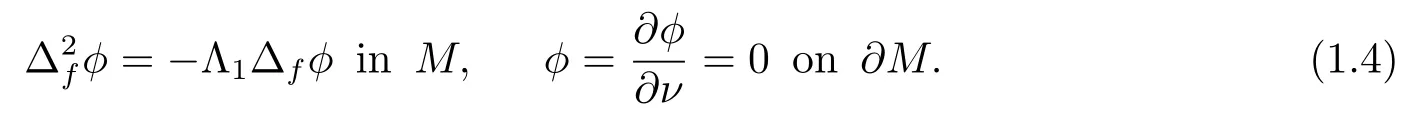
Then we have

with equality holds if and only ifMis isometric to ann-dimensional Euclidean unit semisphere of radius ofandfis constant.
Remark 1.3Compared with Theorems 1.7 and 1.8 in [6], we don’t need to assume that the weighted mean curvature of?Mis bounded in Theorems 1.1 and 1.2.
The study of Steklov eigenvalue problem was started by Steklov[20],his motivation came from physics.From then on, for the Steklov eigenvalue problem, many interesting results were obtained in [2, 3, 15, 16, 22, 23].Recently, some results for the Steklov eigenvalues of the drifting Laplacian were given in [4, 12].In this paper, we consider the following two fourth order Steklov eigenvalue problems for the drifting Laplacian
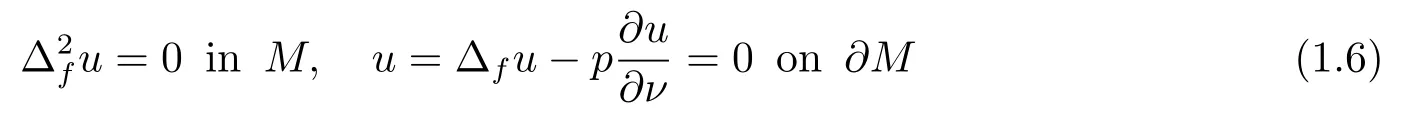
and
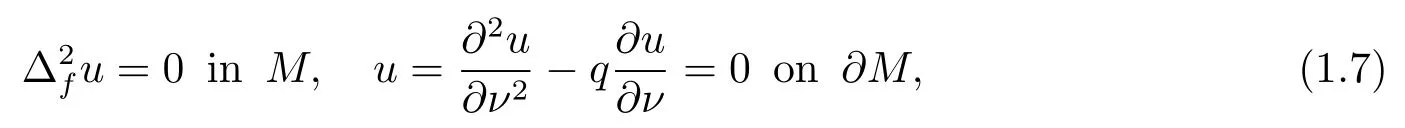
whereνdenotes the outward unit normal vector field of?M.Then, we obtain
Theorem 1.4LetMbe ann(≥2)-dimensional compact connected smooth metric measure space with boundary?Mand non-negativem-weighted Ricci curvature.Letp1,q1be the first nonzero eigenvalue of problems (1.6) and (1.7), respectively.Then we have

the equality holds in(1.8)if and only ifMis isometric to an Euclidean ball andfis constant.
Theorem 1.5LetMbe ann(≥2)-dimensional compact connected smooth metric measure space with boundary?M.Assume thatm-weighted Ricci curvature is bounded below by?(m ?1)κfor some nonnegative constantκ, and the weighted mean curvature ofMis bounded belowwith a positive constantc.Letλ1be the first Dirichlet eigenvalue of the deifting Laplacian, and letp1is the first nonzero eigenvalue of the Steklov problem (1.6) , then we have

the equality holds in (1.9) if and only ifMis isometric to an Euclidean ball of radius 1/candfis constant.
2 Proofs of Theorem 1.1–Theorem 1.2
In this section, we give the proofs of Theorem 1.1–Theorem 1.2 listed in Section 1.Before proving these results, we first recall some notations.LetMbe ann-dimensional compact manifold with boundary.We often writethe Riemannian metric onMas well as that induced on?M.Let?and ?fbe the connection and the drifting Laplacian onM, respectively.Letνbe the unit outward normal vector of?M.The shape operator of?Mis given byS(X) =?Xνand the second fundamental form of?Mis defined ashereX,Y ∈T?M.The eigenvalues ofSare called the principal curvatures of?Mand the mean curvatureHof?Mis given byhere trSdenotes the trace ofS.We can now state Reilly-type formula (see [17, Theorem 1]).For a smooth functiongdefined onM, the following identity holds if
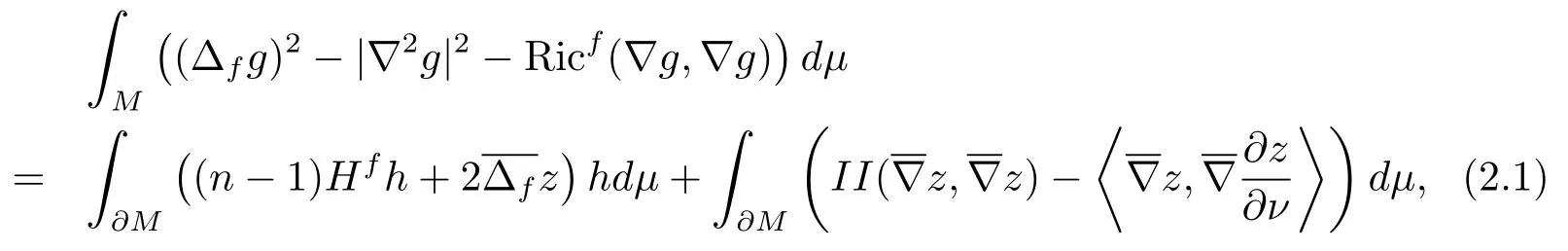

Substituting (2.2) into (2.1), and it then follows from the definition of them-Bakrymery Ricci tensor that
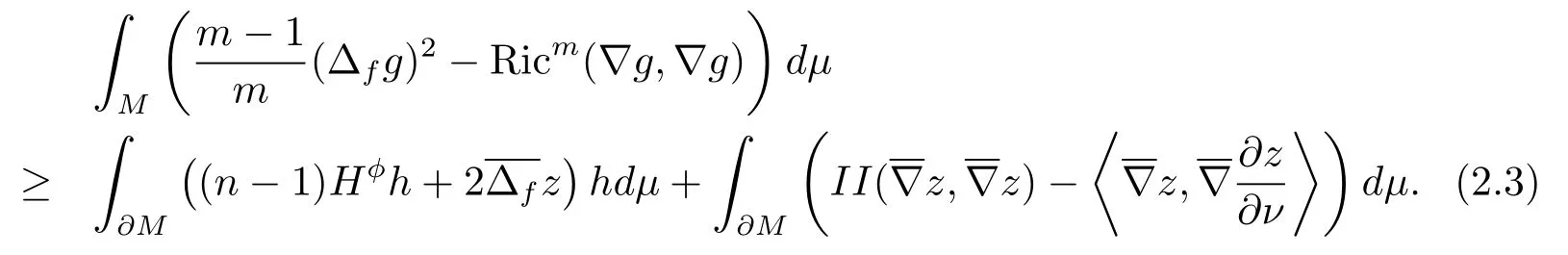
Remark 2.6(i) Whenm=n, we know thatfis a constant, then ?f= ?, (2.1)becomes classic Reilly formula [19], the equality holds in (2.3) if and only if
(ii) Whenm>n, the equality holds in (2.3) if and only ifUsing inequality (2.3), we give the proofs of Theorem 1.1–Theorem 1.2.
Proof of Theorem 1.1Letgbe an eigenfunction of problem (1.2) corresponding to the first eigenvalue Γ1.That is
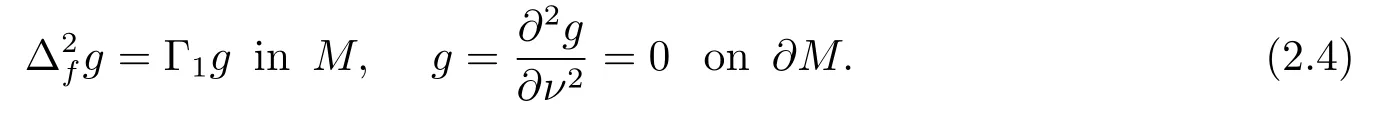
Multiplying (2.4) bygand integrating onM, we infer from the divergence theorem that
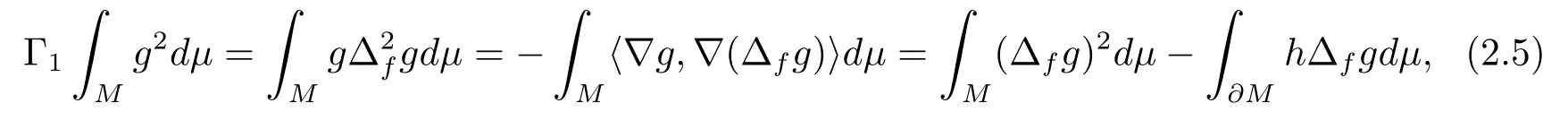
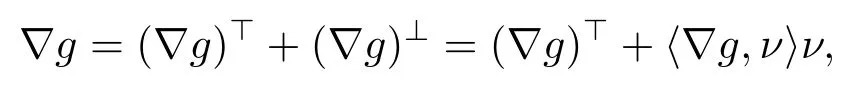
where(?g)is tangent to?Mand(?g)⊥is normal to?M.Then fromwe have
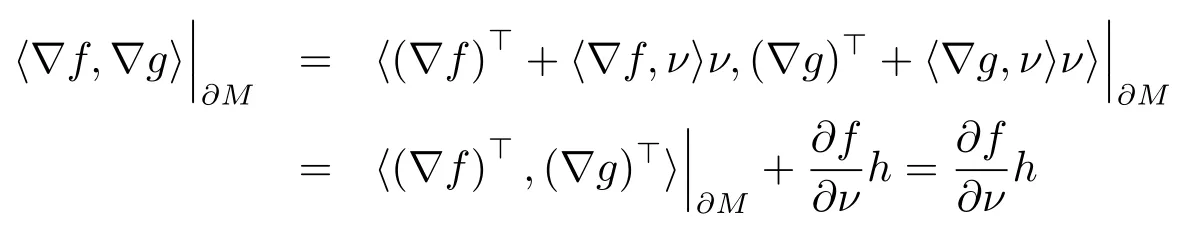
and
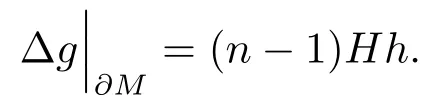
So, we infer from above two equalities that
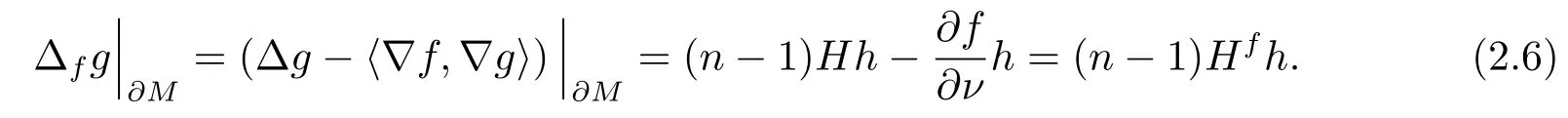
Combining (2.5) and (2.6), we have
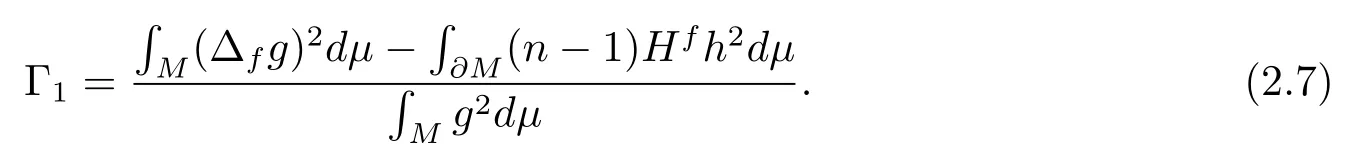
Takingginto (2.3), we have
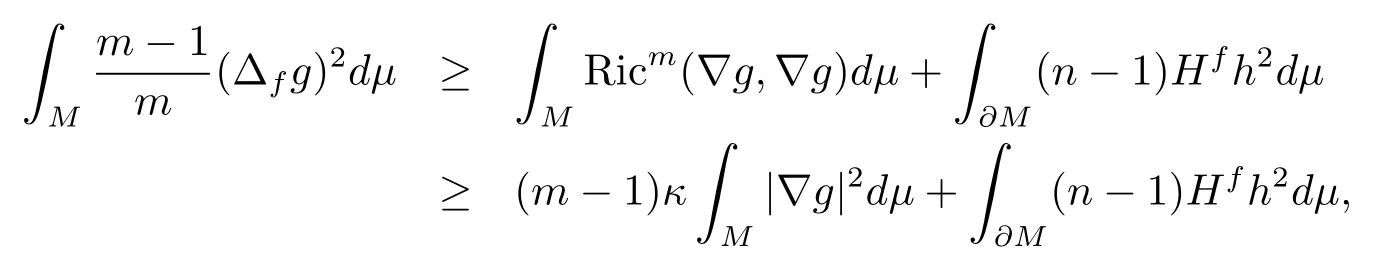
which implies
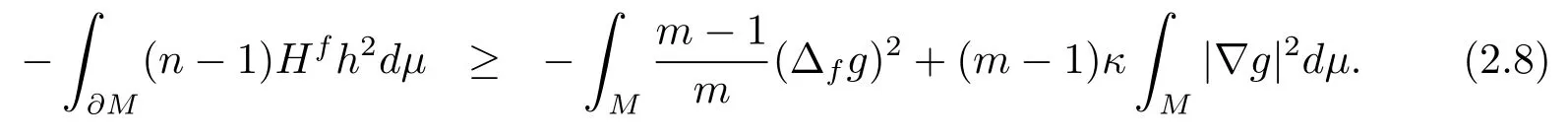
Combining (2.7) and (2.8), we have
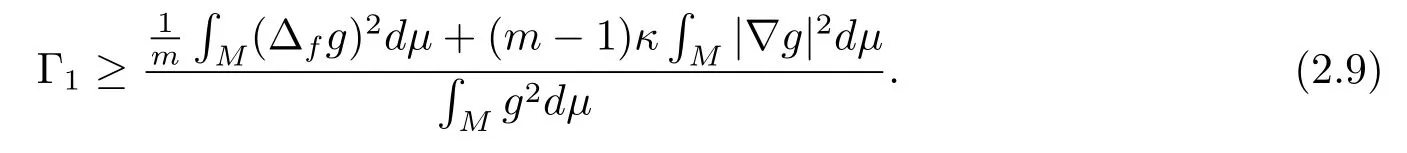
For any nonzero function which vanishes on?M,it is well known from the Poincarinequality and the Schwarz inequality that
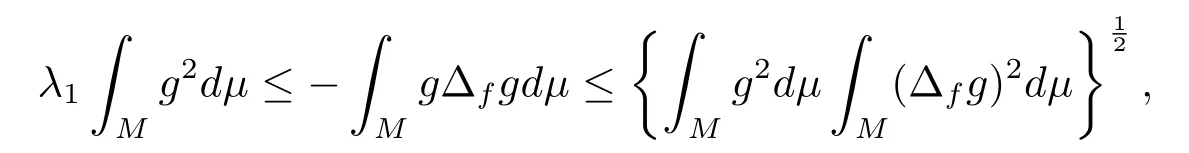
which implies that
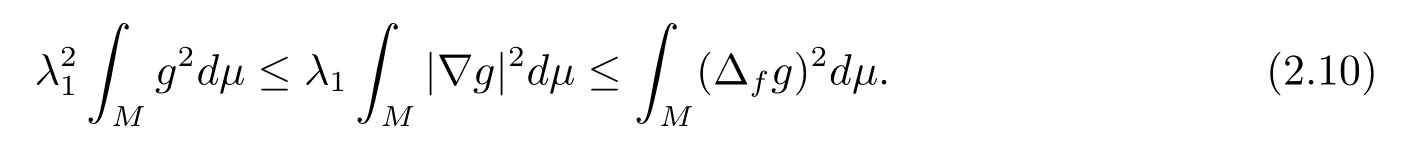
The equality holds in above inequality if and only ifgis the a first Dirichlet eigenfunction of the drifting Laplacian ofM.
Combining (2.9) and (2.10), we have
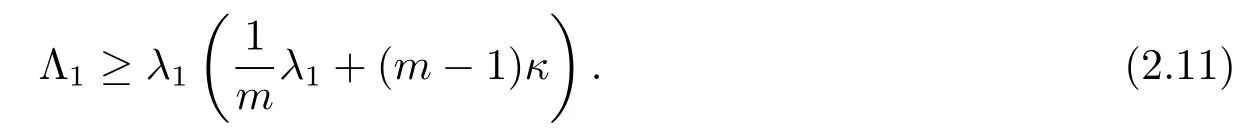
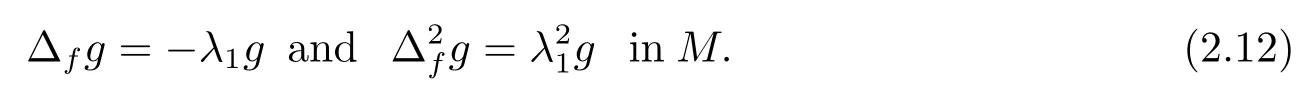
Whenm=n, thenfis a constant and ?f= ?, from [24, Theorem 1.1], we know thatwith equality holding if and only ifMis isometric to ann-dimensional Euclidean unit semi-sphere.
Whenm>n,we know that equality holds in(2.3),which means
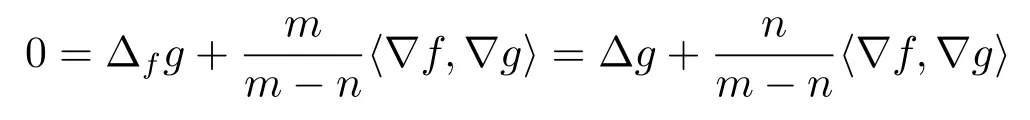
holds everywhere onM.Multiplying in above inequality withgand integrating onMwith respect togive that
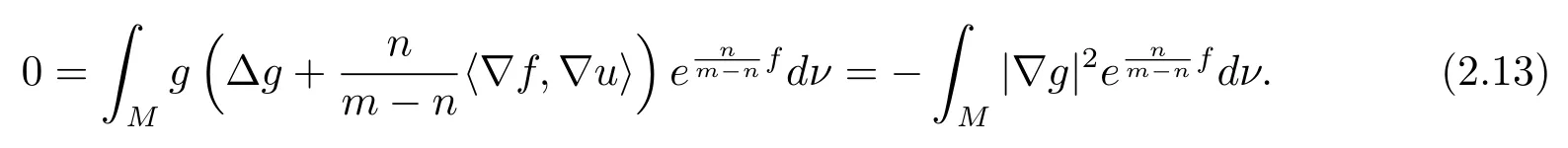
From above equality, we know thatgis a constant function onM, which is a contradiction sincegis the first eigenfunction of drifting Laplacian and cannot be a constant.Therefore,we know thatwith equality holding if and only ifMis isometric to ann-dimensional Euclidean unit semi-sphere andfis a constant.This completes the proof of Theorem 1.1.
Proof of Theorem 1.2Letφbe an eigenfunction of problem (1.4) corresponding to the first eigenvalue Λ1.That is
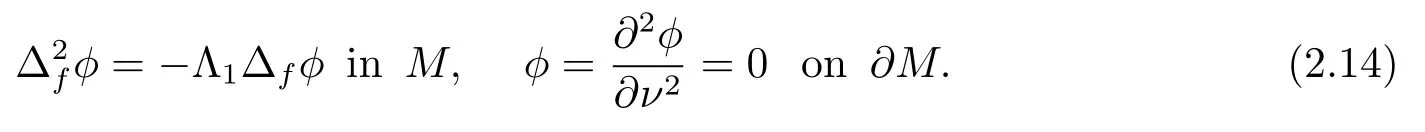
Multiplying (2.14) byφand integrating onM, we infer from the divergence theorem that
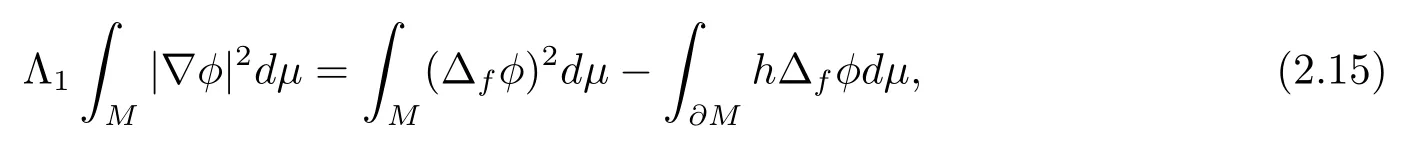
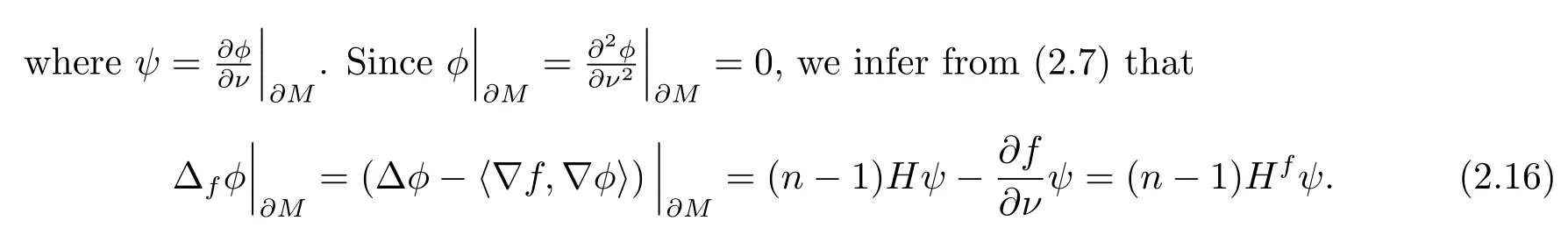
Combining (2.15) and (2.16), we have
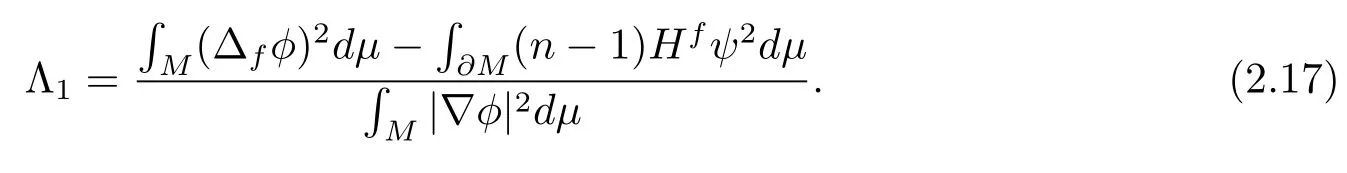
Takingφinto (2.3), we have
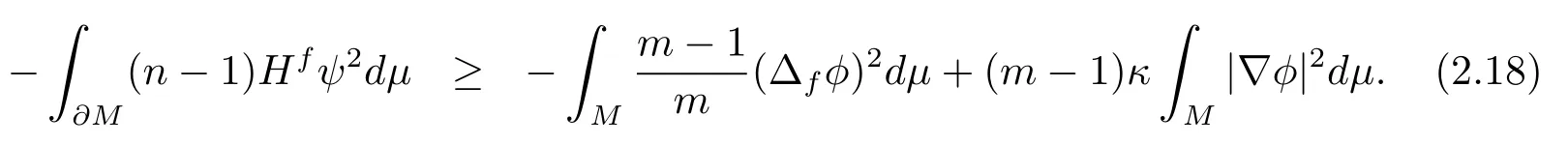
Combining (2.17)–(2.18), we have
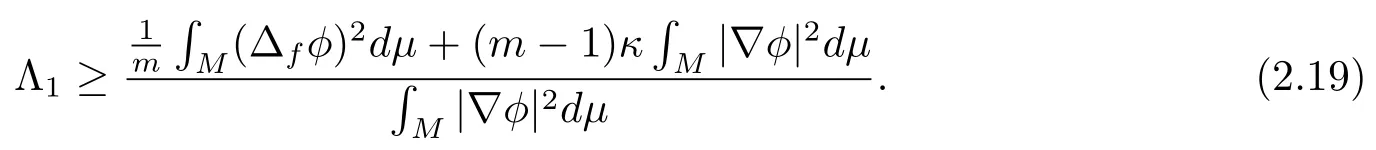
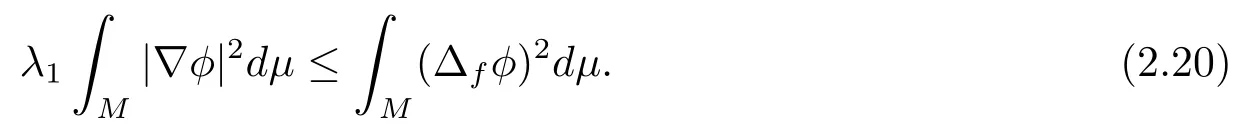
Taking above inequality into (2.19), we havethe equality holds in above inequality if and only ifφis the first Dirichlet eigenfunction of the drifting Laplacian ofM.
Whenm=n, thenfis a constant and ?f= ?, from [24, Theorem 1.2], we know thatwith equality holding if and only ifMis isometric to ann-dimensional Euclidean unit semi-sphere.
Whenm>n, ifwe know that equality holds in (2.3), then by similar discussion in the proof of Theorem 1.1, we know thatuis a constant function onM,which is a contradiction sinceφis the first eigenfunction of drifting Laplacian and cannot be a constant.Therefore, we haveThis completes the proof of Theorem 1.2.
3 Proofs of Theorem 1.4–Theorem 1.5
In this section, we give the proof of Theorem 1.4–Theorem 1.5 listed in Section 1.
Proof of Theorem 1.4Letwbe an eigenfunction corresponding to first eigenvalueq1of problem (1.7), that is
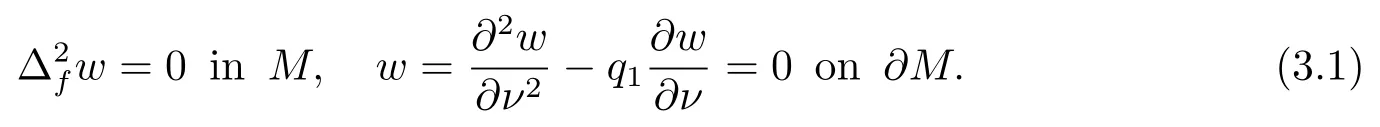
We know thatwis not a constant sinceOtherwise,ifη=0, we have
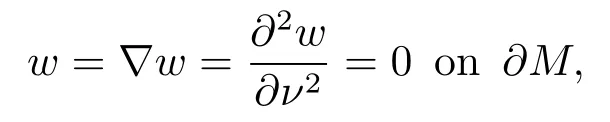
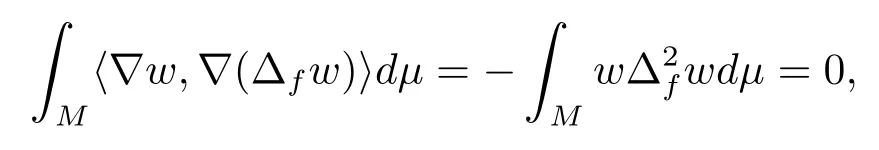
which implies that
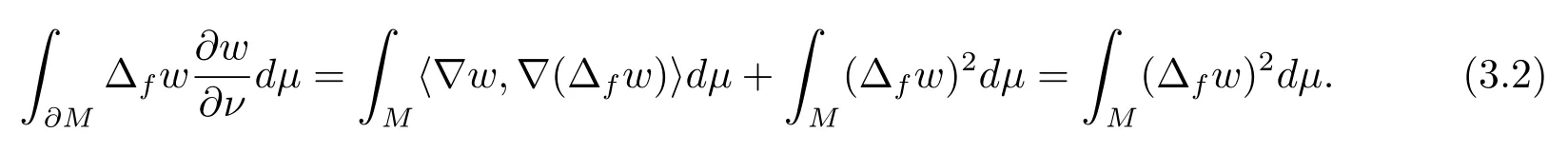
On the other hand, since
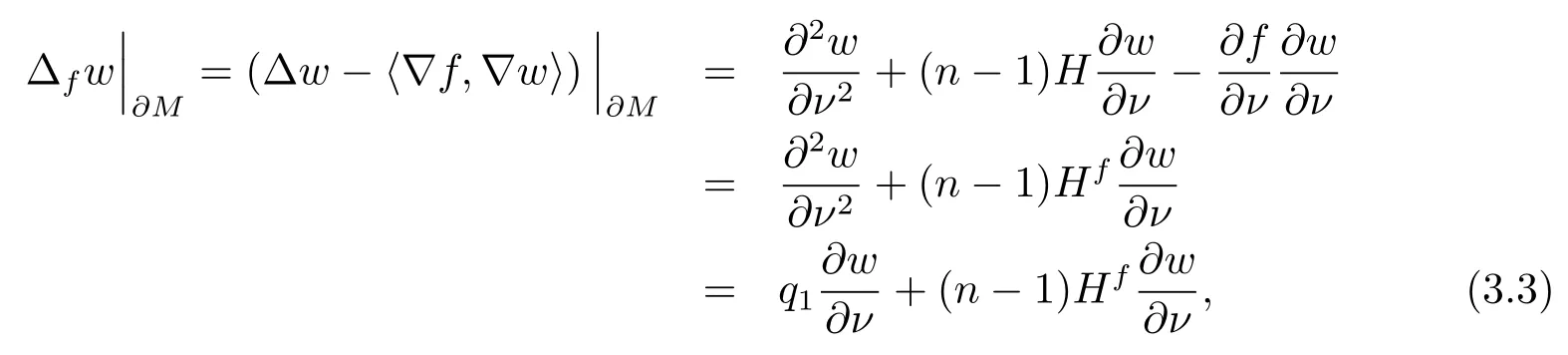
we can get
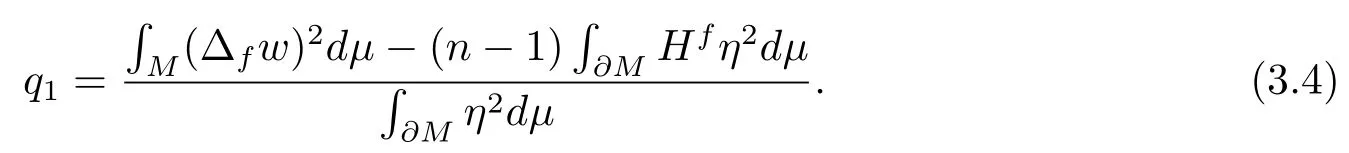
Substitutingwinto (2.3) and noticingthen we have
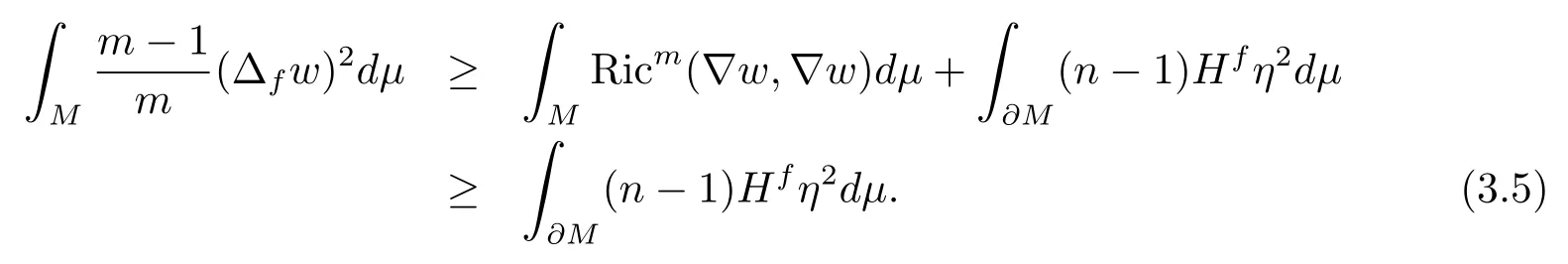
Combining (3.4) and (3.5), we have

Sincep1is given by

we have from the variational characterization that

Combining (3.6) and (3.8), we have
Whenm=n, thenfis constant, so ?f= ?, then by Theorem 1.3 in [24], we know that equality holds in (1.8) if and only ifMis isometric to an Euclidean ball.
Whenm>n, if the equality holds in (1.8), the equality holds in (2.3), then ?fw=multiplying withfand integrating onMwith respect towe can get
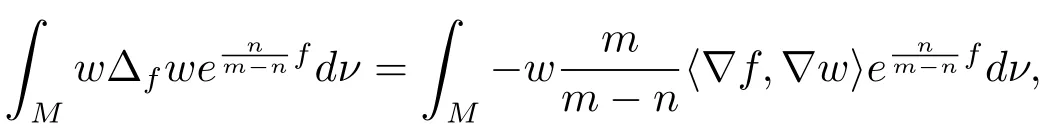
Proof of Theorem 1.5Let?be an eigenfunction corresponding to first eigenvaluep1of problem (1.6), that is
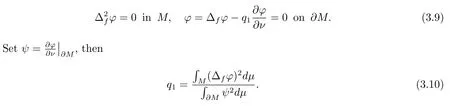
Substituting?into (2.3) and noticingψ=0, Ricm(??,??)≥?(m ?1)κand (n ?1)H? ≥(m ?1)c, then we infer from thatthat
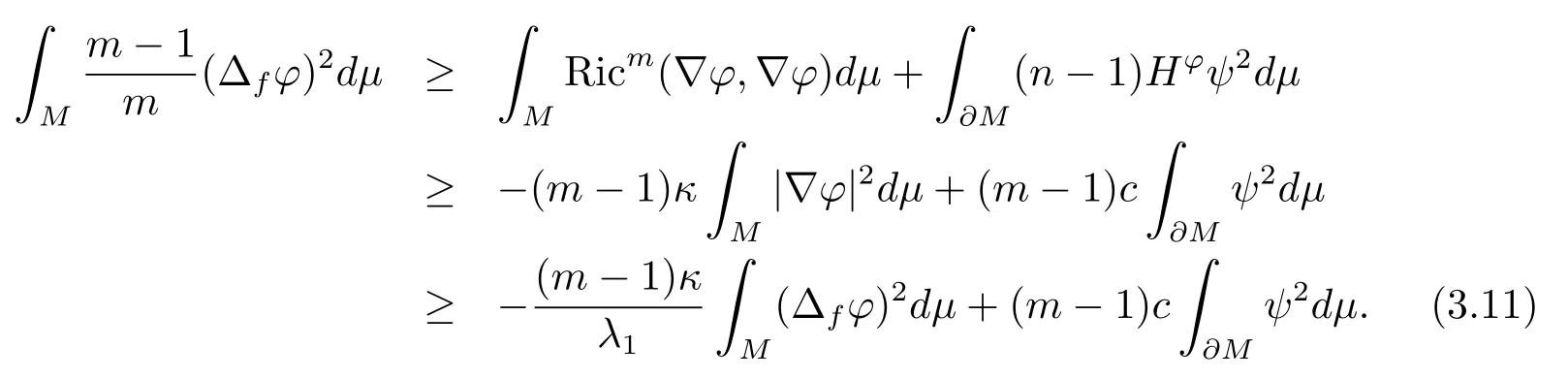
Combining (3.10) and (3.11), we have
Whenm=n, thenfis constant, so ?f= ?, then by Theorem 1.4 in [24], we know that equality holds in (1.8) if and only ifMis isometric to an Euclidean ball.
Whenm>n, if the equality holds in (1.8), the equality holds in (2.3), then by the similar discussion, we know that?is constant, which is a contradiction.Thus, the equality holds in (1.8) if and only ifMis isometric to an Euclidean ball of radius 1/candfis constant.
- 數(shù)學(xué)雜志的其它文章
- LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
- BOUNDEDNESS OF THE FRACTIONAL INTEGRAL OPERATOR WITH ROUGH KERNEL AND ITS COMMUTATOR IN VANISHING GENERALIZED VARIABLE EXPONENT MORREY SPACES ON UNBOUNDED SETS
- IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
- A CLASS OF NON-MATCHABLE DISTRIBUTIVE LATTICES
- 素的?-代數(shù)上的非線性混合Lie三重ξ-導(dǎo)子
- 兩類圖的符號(hào)全控制數(shù)

