A CLASS OF NON-MATCHABLE DISTRIBUTIVE LATTICES
WANG Xu, ZHAO Xu-xu, YAO Hai-yuan
(College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China)
Abstract: In this paper, we consider non-matchable distributive lattices.By introducing the meet-irreducible cell with respect to a perfect matching of a plane elementary bipartite graph and giving its characterizations, we obtain a new class of non-matchable distributive lattices, and extend a result on non-matchable distributive lattices with a cut element.
Keywords: plane (weakly) elementary bipartite graph; Z-transformation directed graph;meet-irreducible cell; non-matchable distributive lattice; planarity
1 Introduction
Zhang et al.[1]introduced a concept ofZ-transformation graph(called by some authors resonance graph) on the set of perfect matchings (or 1-factors) of a hexagonal system, then Zhang and Zhang [2]extended the concept to a general plane bipartite graph with a perfect matching, and Zhang [3]surveyed rich theoretical results in several directions.LetGbe a plane bipartite graph with a perfect matching.Denote byM(G)the set of all perfect matchings ofG.TheZ-transformation directed graphG) is an orientation ofZ-transformation graph [4].
Lam and Zhang[5]proved thatM(G)equipped with a partial order is a finite distributive lattice and its Hasse diagram is isomorphic toG).Recently,Zhang et al.[6]introduced the concept of matchable distributive lattice and got some consequences on matchable distributive lattices, Yao and Zhang [7]obtained some results on non-matchable distributive lattices with a cut element.
In a finite lattice, an element is meet-irreducible if it is covered by exactly one element;from a graphical point of view if and only if it is a vertex of indegree 1 in Hasse diagram.Consider an arcfwith its tailMin(G).We introduce the concept of meet-irreducible cell with respect toM.Furthermore, we have some equivalent characterizations of the concept (i.e., Theorem 3.2).Finally, by Theorem 3.2, we extend a result on non-matchable distributive lattices obtained by Yao and Zhang [7](i.e., Theorem 2.3), and obtain a class of non-matchable distributive lattices by Kuratowski’s theorem.
2 Preliminaries
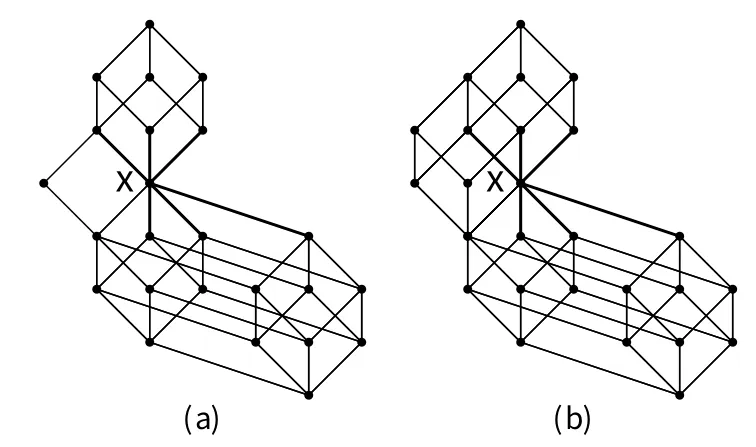
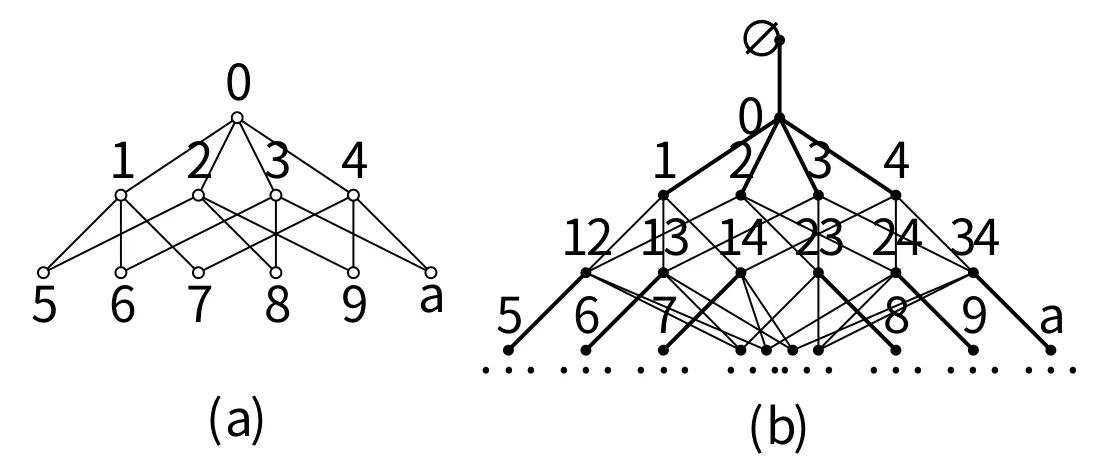
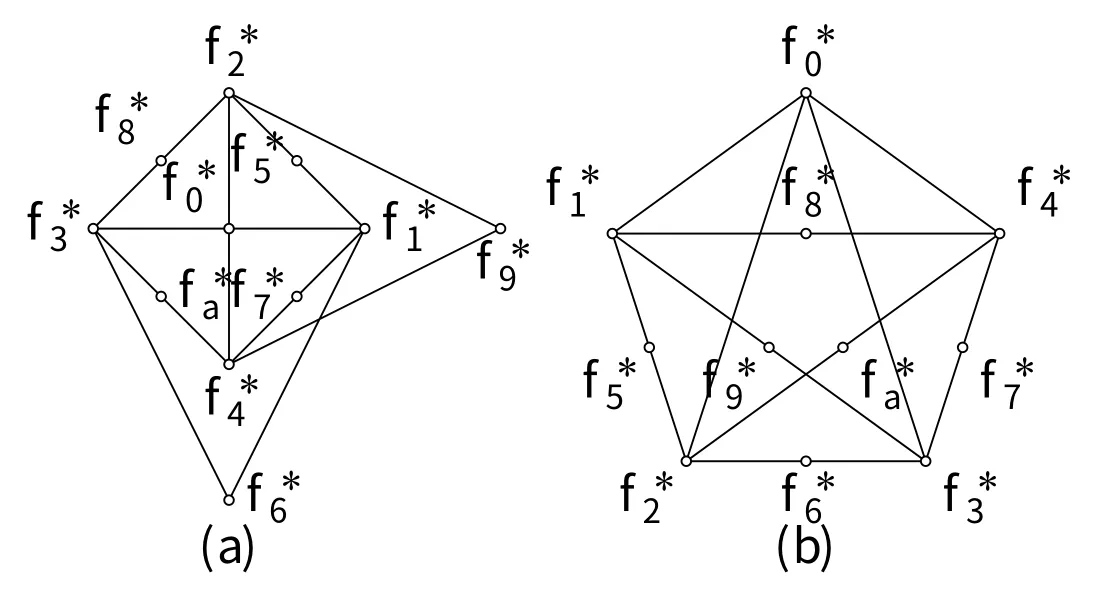
A setPequipped with a binary relation≤satisfying reflexivity, antisymmetry and transitivity is said to be a partially ordered set (poset for short).Given any posetP, the dualP?ofPby definingx ≤yto hold inP?if and only ify ≤xholds inP.A posetPis a chain if any two elements ofPare comparable, and we write n to denote the chain obtained by giving{0,1,···,n?1}the order in which 0<1<··· The symmetric difference of two finite setsAandBis defined asA ⊕B:= (A ∪B)(A ∩B).IfMis a perfect matching of a graph andCis anM-alternating cycle of the graph, then the symmetric difference ofMand edge-setE(C) is another perfect matching of the graph, which is simply denoted byM ⊕C.LetGbe a plane bipartite graph with a matchingM, and the vertices ofGbe colored properly black and white such that the two ends of every edge receive different colors.AnM-alternating cycle ofGis said to be proper,if every edge of the cycle belonging toMgoes from white end-vertex to black end-vertex by the clockwise orientation of the cycle; otherwise improper [8]. For some concepts and notations not explained in the paper, refer to [9, 10]for poset and lattice, [11, 12]for graph theory. An inner face of a graph is called a cell if its boundary is a cycle, and we will say that the cycle is a cell too.Observe that anM-alternating cell intersecting an improperM-alternating cell must be proper, vice versa.Obviously, we have the following result. Lemma 2.1(see[13]) IfGis a plane bipartite graph with a matchingM,then any two proper (resp.improper)M-alternating cells are disjoint. Definition 2.1(see[2]) LetGbe a plane bipartite graph.TheZ-transformation graphZ(G) is defined onM(G):M1,M2∈M(G) are joined by an edge if and only ifM1⊕M2is a cell ofG.AndZ-transformation digraph(G) is the orientation ofZ(G): an edgeM1M2ofZ(G)is oriented fromM1toM2ifM1⊕M2form a properM1-alternating(thus improperM2-alternating) cell. An edge of graphGis allowed if it lies in a perfect matching ofG.A graphGis said to be elementary if its allowed edges form a connected subgraph ofG.LetGbe a bipartite graph.A subgraphHofGis said to be nice ifG ?V(H) has a perfect matching [14];from Theorem 4.1.1 in [14], we have that a bipartite graph is elementary if and only if it is connected and every edge of it is allowed. Definition 2.2(see [2]) A bipartite graphGis weakly elementary if the subgraph ofGconsisting ofCtogether with its interior is elementary for every nice cycleCofG. LetGbe a plane bipartite graph with a perfect matching.A binary relation≤onM(G)is defined as: forM1,M2∈M(G),M1≤M2if and only ifG) has a directed path fromM2toM1[2].It is shown that (M(G);≤) is a poset [5].For convenience, we writeM(G)for poset (M(G),≤). Theorem 2.2(see[5]) IfGis a plane(weakly)elementary bipartite graph,thenM(G)is a finite distributive lattice and its Hasse diagram is isomorphic to(G). Definition 2.3(see [6]) A finite distributive latticeLis matchable if there is a plane weakly elementary bipartite graphGsuch thatLM(G); otherwise non-matchable. Yao and Zhang [7]obtained the following result on non-matchable distributive lattices with a cut element. Theorem 2.3(see [7]) LetLbe a finite distributive lattice, andLhave cut element covered bymelements and coveringnelements.Ifm ≥3 andn ≥3, thenLis nonmatchable. The proof of Lemma 3.7 in [15]implies the following proposition. Proposition 3.1IfGis a plane elementary bipartite graph with a perfect matchingM,then there exists a hypercube in(G) generated by some pairwise disjointM-alternating cells.In particular,Mis the maximum (resp.minimum) element of the corresponding Boolean lattice inM(G) if theseM-alternating cells are proper (resp.improper). It is obvious that the dimension of the hypercube is equal to the number of these pairwise disjointM-alternating cells.In particular, the hypercube is a quadrilateral if and only if it is generated by exactly two disjointM-alternating cells inG[13, 15, 16]. Definition 3.1LetGbe a plane (weakly) elementary bipartite graph with a perfect matchingM.A properM-alternating cellfis meet-irreducible with respect toMifM ⊕fis meet-irreducible inM(G). In fact, by the definition of meet-irreducible element, it follows thatM ⊕fis meetirreducible inM(G)wheneverfis a meet-irreducible cell with respect toM.The equivalent characterizations of meet-irreducible elements is given as follows, the thought of which is analogous to that in [17].A part of Theorem 3.2 is published, however, to make the paper self-contained, we would rather include the proof here than refer to [18]. Theorem 3.2LetGbe a plane (weakly) elementary bipartite graphGwith a perfect matchingMand letfbe a properM-alternating cell. (1) IfGhas no improperM-alternating cell (namely,Mis the maximum element ofM(G)), then every (proper)M-alternating cell is a meet-irreducible cell with respect toM. (2) IfGhas some improperM-alternating cells, then the following are equivalent: (a) the cellfis a meet-irreducible cell with respect toM; (b) the cellfintersects every improperM-alternating cell; (c) there is no perfect matchinginV(Q){M}such thatfis a proper-alternating cell, whereQis a corresponding Boolean lattice generated by all improperM-alternating cells. Proof(1) It is trivial by the definition ofZ-transformation directed graph. (2) First suppose that the cellfis a meet-irreducible cell with respect toM, but there is at least one improperM-alternating cellsuch thatfandare disjoint.Thusi.e.,Ghas two improperM ⊕f-alternating cells, henceM ⊕fis not meet-irreducible, contradicting the supposition thatfis a meet-irreducible cell with respect toM. Next suppose that the cellfintersects every improperM-alternating cell, but there is a perfect matchinginV(Q){M} such thatfis a proper-alternating cell.In fact, by Proposition 3.1, there is at least one improperM-alternating celthat is a properalternating cell.Hencefandare disjoint by Lemma 2.1, a contradiction. Finally, suppose that there is no perfect matchinginV(Q){M} such thatfis a properalternating cell, butfis not a meet-irreducible cell with respect toM.ThusGhas at least one improperM ⊕f-alternating cellexceptf, by Lemma 2.1, hencefandare disjoint.Thereforeis an improperM-alternating cell, which implies thatfis a properM ⊕alternating cell, i.e., there is a perfect matchingsuch thatfis a properalternating cell, a contradiction. Assume that every properM-alternating cell is a meet-irreducible cell with respect toM.IfGhas an improperM-alternating cell,then every properM-alternating cell intersects every improperM-alternating cell, henceMis a cut element [13].AndMis the maximum element ofM(G) otherwise.Moreover we obtain the following consequence of Theorem 3.2. Corollary 3.3(see [4, 13]) IfGis a plane elementary bipartite graph with a perfect matchingM,and has both proper and improperM-alternating cells,thenMis a cut vertex ofZ(G) if and only if every properM-alternating cell intersects every improperM-alternating cell, i.e., every properM-alternating cell is a meet-irreducible cell with respect toM. Note that duality of lattice, meet-irreducible cell, Theorem 3.2 and Corollary 3.3 could be treated in dual. Subdividing an edgeeis to deletee, add a new vertexv, and joinvto the ends ofe.Any graph derived from a graphGby a sequence of edge subdivisions is called a subdivision ofG. Given a plane graphG, its(geometric)dualG?is constructed as follows: place a vertex in each face ofG(including the exterior face) and, if two faces have an edgeein common,join the corresponding vertices by an edgee?crossing onlye[12].It is easy to see that the dualG?of a plane graphGis itself a plane graph [11]. Theorem 4.1(Kuratowski’s theorem) A graph is planar if and only if it contains no subdivision of eitherK5orK3,3. Similar to the proof of Lemma 4.2 in [7]and Theorem 3.2, we have Theorem 4.2. Theorem 4.2LetLbe a finite distributive lattice andx ∈L.Ifxis covered by at least three elements and covers at least three meet-irreducible elements,thenLis non-matchable. ProofSuppose to the contrary thatLis matchable.Then there is a plane (weakly)elementary bipartite graphGsuch thatM(G)[6],which implies that a perfect matchingMxofGcorresponds tox ∈L.According to the premise,Ghas at least three improperMxalternating cells, and at least three properMx-alternating cellsf1,f2andf3that are meetirreducible.By Theorem 3.2, such three properMx-alternating cells intersect all improperMx-alternating cells.This shows that the dualG?ofGcontains aK3,3as subgraph.But it is impossible by Kuratowski’s theorem. Figure 1: two non-matchable distributive lattices Ifxis a cut element, Theorem 4.2 implies Theorem 2.3(i.e., Theorem 4.3 in[7]); on the other hand, Theorem 4.2 can determine some non-matchable distributive lattice that can not be determined only by Theorem 2.3.For instance,it is easy to see that each distributive lattice in Figure 1 is non-matchable by Theorem 4.2, but not determined only by Theorem 2.3. Obviously, a dual version of Theorem 4.2 could be obtained easily. Corollary 4.3IfLis a matchable distributive lattice, then for every element ofL, it either is covered by at most two elements or covers at most two meet-irreducible elements in bothLandL?. Figure 2: (a) the poset ? and (b) a part of F(?) LetPbe a poset andF ?P.The subposetFis a filter if, wheneverx ∈F,y ∈Pandx ≤y, we havey ∈F[9].The set of all filters of a posetPis denoted byF(P),and carries the usual anti-inclusion order; and the filter latticeF(P) is a distributive lattice[9, 10].Figure 2 (a) shows the Hasse diagram of a poset ?; and Figure 2 (b) is the highest five layers of Hasse diagram ofF(?), where every filter is labeled by its minimal element(s).Combining Theorem 3.2 and Kuratowski’s theorem, we have another class of non-matchable distributive lattices. Theorem 4.4The distributive latticeF(?)is non-matchable, where ? is the poset as shown in Figure 2(a). Figure 3: proof of Theorem 4.4 ProofRecall thatF(?) is a finite distributive lattice.Suppose thatF(?) is matchable.SinceF(?) has a cut element labeled by 0 (see Figure 2), and is irreducible, there exists a plane elementary bipartite graphGsuch that Consider a part ofF(?)as drawn in Figure 2(b).The vertices?,0,1,···,acorrespond to the perfect matchingsM?,M0,M1,···,MaofG, respectively.Letf0=M?⊕M0,f1=M0⊕M1,f5=M12⊕M5,f6=M13⊕M6,···, andfa=M34⊕Ma.By definition ofZ-transformation graph,thenf0is a nice cell,so aref1,···,fa.Since the cellsf0,f1,···,faare meet-irreducible cells,by Theorem 3.2(2),the cellf0intersectsf1,f2,f3andf4;the cellf5intersectsf1andf2, but it does not intersectf3orf4, becausef5,f3andf4are properM12-alternating cells.Thusf0andf5are distinct; analogously,f0andfi(i ∈{6,7,8,9,a})are distinct too. Next, consider the dualG?ofG, as drawn in Figure 3 (a), vertexis adjacent withis adjacent withetc.Therefore, letthusG?contains a subgraphClearlyS?(see Figure 3 (b)) is a subdivision ofK5.By Kuratowski’s theorem, henceS?is non-planar, contradicting the planarity ofG. If a posetPcontains ?as a convex subposet, then there are 11 elements inPcover relations of which are identical in ?.Similar to proof of Theorem 4.4,we prove the following result. Corollary 4.5LetPbe a poset containing ?as a convex subposet.Then distributive latticeF(P)is non-matchable.In addition,for any finite distributive latticeL,the Cartesian product, linear sum and vertical sum [9]ofF(P) andLare non-matchable. Note that ?is a filter of 24, the following corollary is immediate. Corollary 4.6The distributive latticeF(24) is non-matchable.In addition, the distributive latticeis non-matchable, wherek ≥4, njis a chain of lengthnjandnj ≥2 for everyj=1,2,···,k.3 Meet-Irreducible Cell
4 Non-Matchable Distributive Lattices
- 數(shù)學雜志的其它文章
- LEONARD PAIRS CONSTRUCTED FROM THE QUANTUM ALGEBRA νq(sl2)
- BOUNDEDNESS OF THE FRACTIONAL INTEGRAL OPERATOR WITH ROUGH KERNEL AND ITS COMMUTATOR IN VANISHING GENERALIZED VARIABLE EXPONENT MORREY SPACES ON UNBOUNDED SETS
- IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
- SHARP ESTIMATES FOR EIGENVALUES OF BI-DRIFTING LAPLACIAN
- 素的?-代數(shù)上的非線性混合Lie三重ξ-導子
- 兩類圖的符號全控制數(shù)

