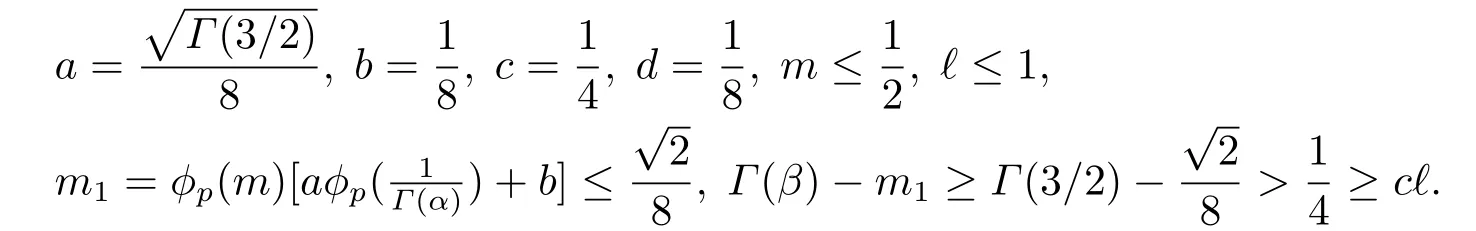Solvability for Fractional p-Laplacian Differential Equation with Integral Boundary Conditions at Resonance on Infinite Interval
LIU Zongbao(劉宗寶),LIU Wenbin(劉文斌),ZHANG Wei(張偉)
( 1.Department of Fundamental Course,Wuxi Institute of Technology,Wuxi 214121,China;2.School of Mathematics,China University of Mining and Technology,Xuzhou 221116,China)
Abstract: In this paper,we investigate the existence of solutions for a class of fractional integral boundary value problems with p-Laplacian operator at resonance on infinite interval,by using Mawhin’s continuation theorem.An example is given to show the application of our main result.
Key words: Fractional boundary value problem; p-Laplacian operator; Resonance;Infinite interval; Mawhin’s continuation theorem
1.Introduction
Fractional calculus is a generalization of the classical integer order calculus.In contrast to the integer order calculus,fractional calculus has nonlocal behavior.This characteristic lets fractional differential equation be an excellent tool in describing some complex problems.For example,in the description of memory and hereditary properties of various materials and processes.[1?2]Besides,the fractional calculus and its applications appear frequently in various fields,such as physics,chemistry,biology,control theory,economics,biophysics,signal and image processing,etc.[3?8]The height loss over time of the granular material contained in a silo can be modeled with fractional derivatives as follows:
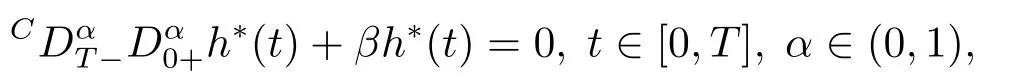
whereis the Riemann-Liouville fractional derivative andis the right-sided Caputo fractional derivative,h?(t)=hbed?h(t)represents an investigated function,hbedis the initial bed height,h(t)is the height loss of the granular bed due to silo emptying[3].
Differential equations with integral boundary conditions have various applications in applied fields.[9?10]In the past few years,this kind of boundary value problems (short for BVPs)has drawn increasing attention of scholars.[10?17]
In[11],YANG,MIAO and GE considered the following integral BVPs by using extension of Mawhin’s continuation theorem.
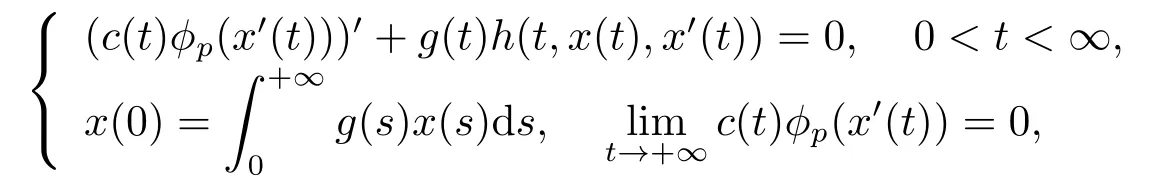
whereh:[0,+∞)×R2→R satisfies g-Carath′eodory conditions,?pis ap-Laplacian operator,defined as?p(s)=|s|p?2s(s≠0),?p(0)=0.
In [12],Cabada and WANG investigated the following fractional differential equations with integral boundary value conditions by using Guo-Krasnoselskii fixed point theorem.
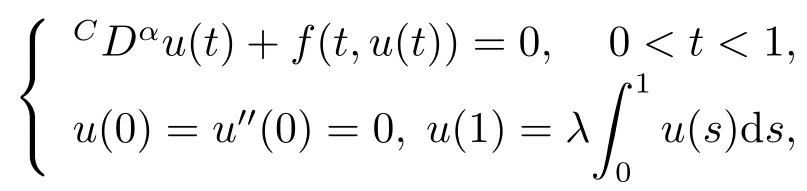
where 2<α<3,0<λ<2,CDαis the Caputo fractional derivative andf:[0,1]×[0,+∞)→[0,+∞)is a continuous function.
In[13],JIANG studied the following fractional differential equations with integral boundary value conditions on the half line by using Mawhin’s continuation theorem.
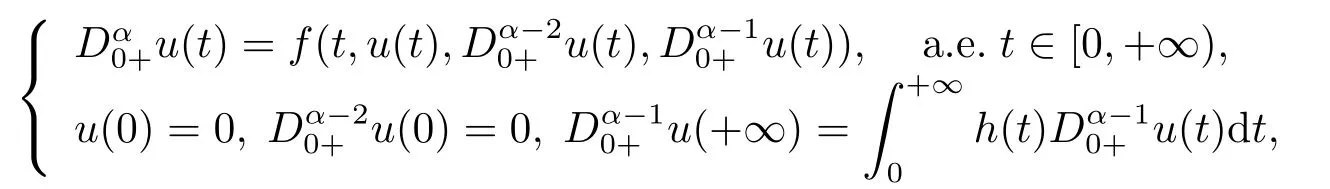
whereis the standard Riemann-Liouville fractional derivative with 2< α ≤3 andf:[0,+∞)×R3→R satisfies Carath′eodory conditions.
Recently,the existence of solutions to boundary value problems of fractional differential equations on infinite interval has been extensively studied.[13,16,18?23]However,to the best of our knowledge,the research has proceeded more slowly for fractional boundary value problems on infinite interval withp-Laplacian operator,especially for resonance problem.Thus,motivated by the results mentioned,in this paper,we discuss the following integral boundary value problems by using Mawhin’s continuation theorem.

whereandare the standard Riemann-Liouville fractional derivative with 1<α,β ≤2,?pis ap-Laplacian operator,g(t)>0 andg(t)∈L1[0,+∞),with
Throughout this paper,we assume that the following conditions hold:
(A1)w(t)>0 on [0,+∞)and(tβ?1/w(t))∈C[0,+∞)∩L1[0,+∞);
(A2)f:[0,+∞)×R3→R is anL1-Carath′eodory function,that is,fsatisfies Carath′eodory conditions,and for eachr >0,there exists a nonnegative functionφr(t)∈L1[0,+∞)such that|f(t,x,y,z)|≤φr(t)for all
RemarkThe condition (A1)implies that
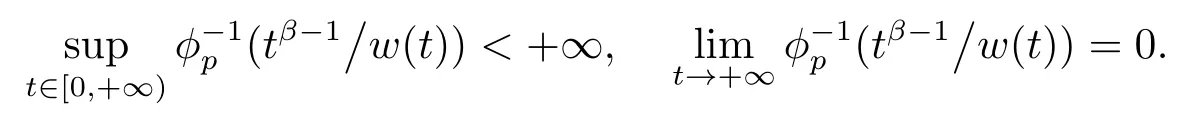
The rest of this paper is built up as follows.In Section 2,we recall some definitions and lemmas.In Section 3,based on the Mawhin’s continuation theorem,we establish an existence result for the problem (1.1).In Section 4,an example is given to illustrate the usefulness of our main results.
2.Preliminaries
In this section,we present some definitions and lemmas.
LetXandZbe two Banach spaces with the norms||·||Xand||·||Z,respectively.LetL:dom(L)?X→Zbe a Fredholm operator with index zero,P:X→X,Q:Z→Zbe two projectors such that
ImP=KerL,ImL=KerQ,X=KerL ⊕KerP,Y=ImL ⊕ImQ,then,L|domL∩KerP:domL→ImLis invertible.We denote the inverse byKp.Let?be an open bounded subset ofXand domL∩=?,then the mapN:X→Yis calledL-compact onifQN()is bounded andKP,QN=Kp(I?Q)N:is compact (see [24]).
Lemma 2.1[24]LetL:dom(L)?X→Ybe a Fredholm operator of index zero andN:X→YisL-compact on.Assume that the following conditions are satisfied:
(i)Lu≠λNufor anyu ∈(domLKerL)∩??,λ ∈(0,1);
(ii)Nu /∈ImLfor anyu ∈KerL ∩??;
(iii)deg(QN|KerL ,? ∩KerL,0)=0.
Then the equationLx=Nxhas at least one solution in domL ∩.
Proposition 2.1[25]?phas the following properties:
(i)?pis continuous,monotonically increasing and invertible.Moreover,=?qwithq >1 satisfying 1/p+1/q=1;
(ii)For?s,t ≥0,?p(s+t)≤?p(s)+?p(t),if 1 Next,we introduce the definitions of Riemann-Liouville fractional integrals and fractional derivatives on the half-axis and some lemmas,which can be found in [2,4,6,19]. Definition 2.1The fractional Riemann-Liouville integral of orderα>0 for a functionf:(0,+∞)→R is defined by provided the right-hand side is pointwise defined on (0,+∞). Definition 2.2The Riemann-Liouville fractional derivative of orderα>0 for a functionf:(0,+∞)→R is defined by provided the right-hand side is pointwise defined on (0,+∞),wheren=[α]+1. Lemma 2.2Assume thatf ∈L1[0,+∞),γ >δ >0,then Lemma 2.3Assume thatα>0,λ>?1,t>0,then Lemma 2.4(t)=0 if and only if wherenis the smallest integer greater than or equal toα,ci ∈R,i=1,2,···,n. Take and endowed with the norms Lemma 3.1The problem (1.1)is equivalent to the following BVPs: ProofBy Lemma 2.4,has solution So,(1.1)can be rewritten in the form (3.1)and we can easily verify that (1.1)has a solutionx(t)if and only ifx(t)is the solution of (3.1). Define the linear operatorL:domL ?X→Zand nonlinear operatorN:X→Zas follows: where Then the problem (3.1)is equivalent to the operator equationLx=Nx,x ∈domL. Lemma 3.2The operatorL:domL ?X→Zsatisfies{} ProofBy Lemmas 2.3-2.4 and boundary conditions of (3.1),it is easy to get (3.2).Thus,dim KerL=1 and KerLis linearly homeomorphic to R.Ifz ∈ImL,then there exists a functionx∈domLsuch thatz(t)=Dα0+x(t).Thus,by Lemma 2.4 we have Considering the boundary condition(0)=0 and Lemma 2.3,we have Then,by Lemma 2.2 and Lemma 2.3,we get It follows from the conditionsthat that is,On the other hand,supposez∈Zand satisfies (3.4),takex(t)=Iα0+z(t),thenx ∈domLandLx(t)=Dα0+x(t)=z(t),i.e.,z(t)∈ImL.Consequently,(3.3)is satisfied. Lemma 3.3[22]LetXbe the space of all bounded continuous vector-valued functions on [0,+∞)andS ?X.ThenSis relatively compact if the following conditions hold: (a)Sis bounded inX; (b)All functions fromSare equicontinuous on any compact subinterval of [0,+∞); (c)All functions fromSare equiconvergent at infinity. Let Lemma 3.4Define the linear operatorsP:X→X1andQ:Z→Z1by whereX1:=KerL,Z1:=ImQ.ThenLis a Fredholm operator with index zero. ProofEasily check thatPis a continuous projector with It follows fromx=(x?Px)+PxthatX=KerP+KerL.Forx ∈KerP ∩KerL,that is,x ∈KerPandx ∈KerL,xcan be rewritten asx(t)=ctα?1,c ∈R and 0=(Px)(t)=ctα?1,thus,c=0.So,KerP ∩KerL= {0}.Therefore,X=KerP ⊕KerL.On the other hand,for anyz ∈Z,we have Hence,Qis a continuous projector.Obviously,ImL=KerQ.Setz=(z?Qz)+Qz,then(z?Qz)∈KerQ=ImL,Qz ∈ImQ.So,Z=ImL+ImQ.Furthermore,from KerQ=ImLandQ2z=Qz,we can obtain that ImL ∩ImQ= {0}.Thus,Z=ImL ⊕ImQ.Then,we have dim KerL=dim ImQ=co dim ImL=1,it follows thatLis a Fredholm operator with index zero. Lemma 3.5Define the linear operatorsKp:ImL→domL ∩KerPby thenKpis the inverse of the operatorL|domL∩KerP. ProofObviously,LKpz==z,forz ∈ImL.Besides,forx ∈domL ∩KerP,we have(0)=0 and(0)=0,by Lemma 2.3,we get Thus we arrive at the conclusion thatKp=(L|domL∩KerP)?1. Lemma 3.6Assume that? ?Xbe an open bounded set such that domL ∩≠?,thenNisL-compact on. ProofSince??Xis a bounded set,there existsr>0 such that?{x∈X:||x||X≤r}.By the condition(A2),there existsφr∈L1[0,+∞)such that|f(t,x(t)(t)(t)|≤φr(t),a.e.t∈[0,+∞).Then,for anyx∈,we have So, Thus, Therefore,QN()is bounded.Now we divided three steps to show thatKp(I?Q)N:→Xis compact.For convenience,we let Then,forx ∈,we have and Step 1 We assert thatKp(I?Q)N()is uniformly bounded.Forx ∈,we have and So,Kp(I?Q)N()is uniformly bounded. Step 2 We prove thatKp(I?Q)N()is equicontinuous on any compact subinterval of [0,+∞).In fact,for anyt1,t2∈[0,T]withTis a positive constant.It follows from the uniform continuity ofon [0,T]×[0,T]and the absolute continuity of integral that →0,ast1→t2,and Since Noting that?q(·)is uniform continuous on [??,?],we derive In addition, Thus, From above,we getKp(I?Q)N()is equicontinuous on [0,T]. Step 3 We show a fact thatKp(I?Q)N()is equiconvergent at infinity.In fact,for anyε>0,from (3.5)there existsL1>0 such that Thus,for anyt2>t1≥L,we get By Lemma 3.3,we obtain thatKp(I?Q)N()is compact. In order to obtain our main results,we suppose that the following conditions are satisfied:(A3)There exists a constantA>0 such that if |(t)|>A,x∈domLKerL,t∈[0,+∞),then (A4)There exist nonnegative functionsa(t)(1+tα?1)p?1,b(t),c(t),d(t)∈L1[0,+∞)with (Γ(β)?m1)> c?,if 1< p <2 and (Γ(β)?2p?1m1)> c?,ifp ≥2 such that for allt ∈[0,+∞),(x,y,z)∈R3, where (A5)Forctα?1∈KerL,there exists a constantG>0 such that either or for allc ∈R with|c|>G. Lemma 3.7Set?1= {x ∈domLKerL:Lx=λNx,λ∈(0,1)}.Suppose that (A1)-(A4)hold.Then,?1is bounded. ProofBy Lemma 2.4,forx ∈?1[0,+∞),we have Since(0)=0,we derivec0=0.So, that is, Also,sinceNx ∈ImL=KerQforx ∈?1,thenQNx=0.It follows from (A3)that there existst0∈[0,+∞)such that(t0)|≤A.Thus, Therefore,we can obtain that Then,from (A4),forx ∈?1,t ∈[0,+∞),we have In the case 1 In the casep ≥2,by Proposition 2.1,one has It has been known that If 1 that is, Ifp ≥2,by Proposition 2.1,then that is, Then,if 1 that is, In the same way,ifp ≥2,by (3.12),(3.14),we derive that is, By (3.9),(3.10),(3.15),(3.16),we can get?1is bounded. Lemma 3.8Set?2= {x ∈KerL:QNx=0}.Suppose that (A1),(A2)and (A5)hold,then?2is bounded. ProofForx ∈?2,we havex=ctα?1,c ∈R,andQNx=0,that is, By (A5),we get|c|≤G.That is,?2is bounded. Lemma 3.9Set?3={x ∈KerL:λx+(1?λ)?JQNx=0,λ ∈[0,1]}.whereJ:ImQ→KerLis a homeomorphism given by Suppose(A1),(A2)and(A5)hold,then?3is bounded,where?=1 if(3.7)holds and?=?1 if (3.8)holds. ProofForctα?1∈?3,without loss of generality,we suppose that (3.8)holds,then there existsλ ∈[0,1]such that that is, Ifλ=0,by(A5),we obtain|c|≤G.Ifλ=1,thenc=0.Moreover,forλ∈(0,1),if|c|>G,we have It is a contradiction.So,?3is bounded. Theorem 3.1Suppose(A1)-(A5)hold.Then the problem(3.1)has at least one solution in domL. ProofLetbe a bounded and open set.From Lemma 3.6,we getNisLcompact onBy Lemmas 3.7 and 3.8,we obtain (i)and (ii)of Lemma 2.1 hold.So,we only need to show (iii)holds.Take According to Lemma 3.9,we deriveH(x,λ)=0 forx∈KerL∩??.It follows from the homotopy of degree that By Lemma 2.1,we can get that operator functionLx=Nxhas at least one solution in domL ∩,which equivalent to the problem (1.1)has at least one solution inX. Example 4.1Consider the boundary value problems Chooseα=By simple calculation,we can get TakeA=G=16,then we can easily check that (A1)-(A4)and (3.7)hold.By Theorem 3.1,the problem (4.1)has at least one solution.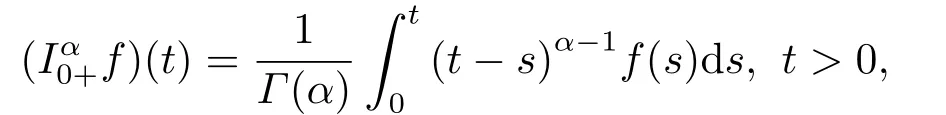
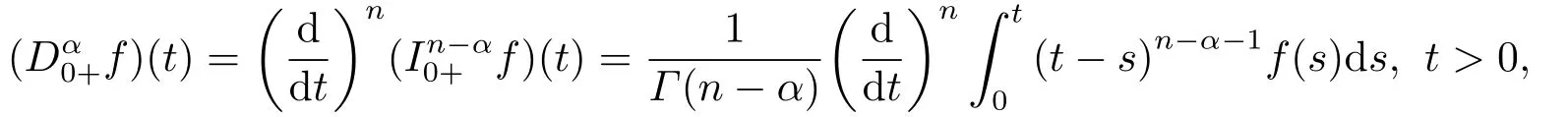
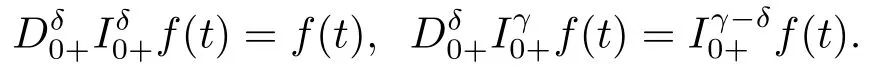


3.Main Result
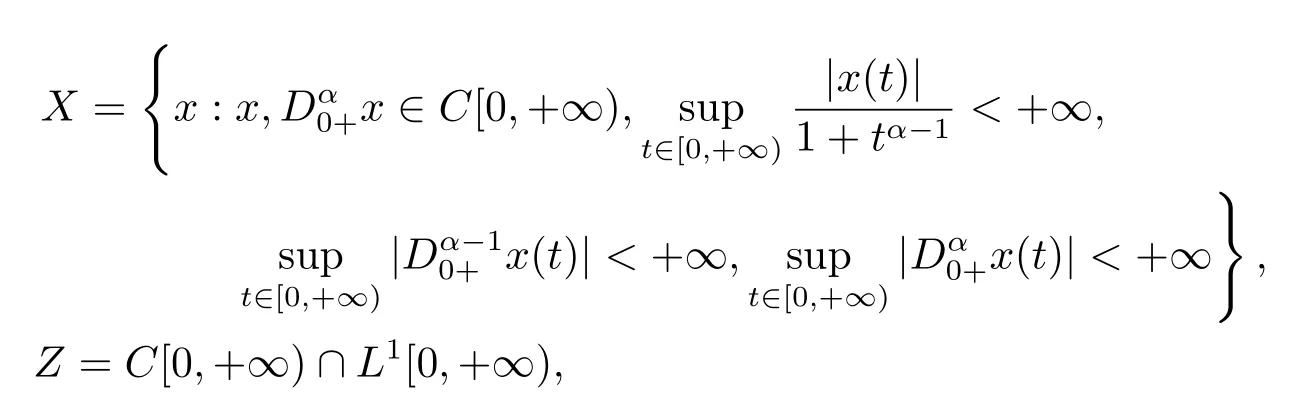
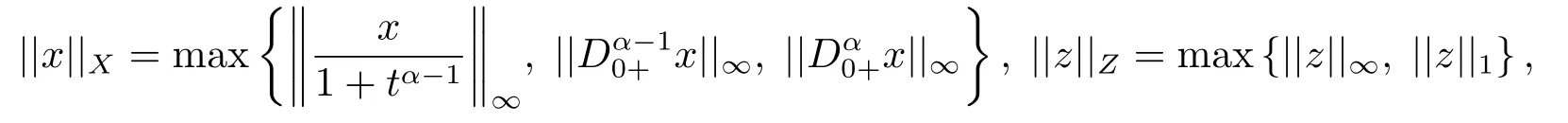
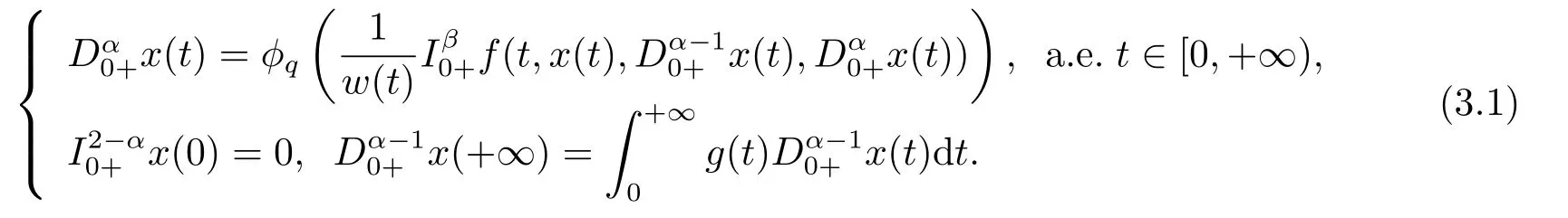
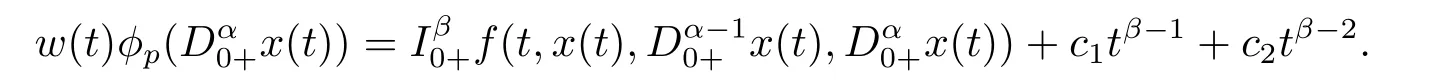

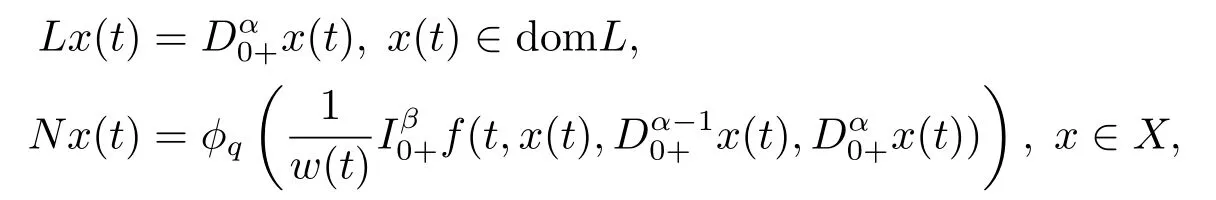


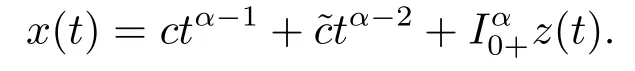
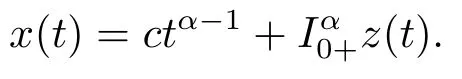
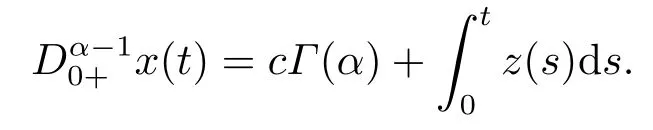

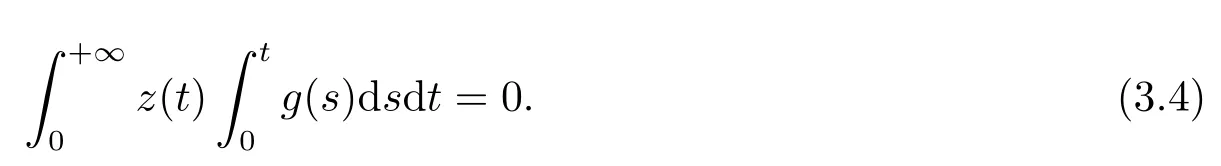
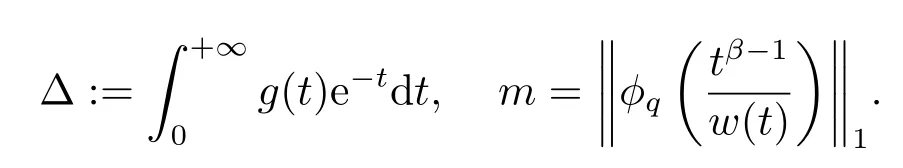



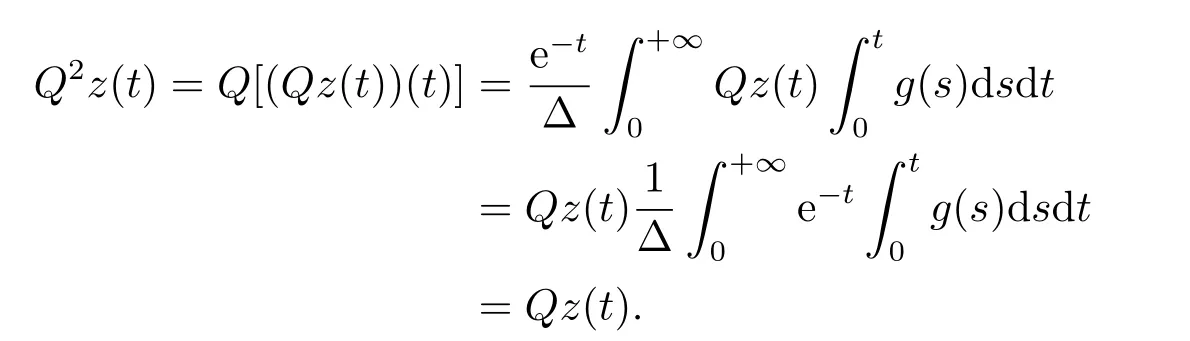
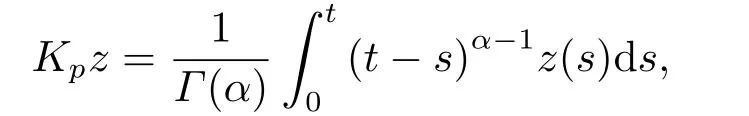

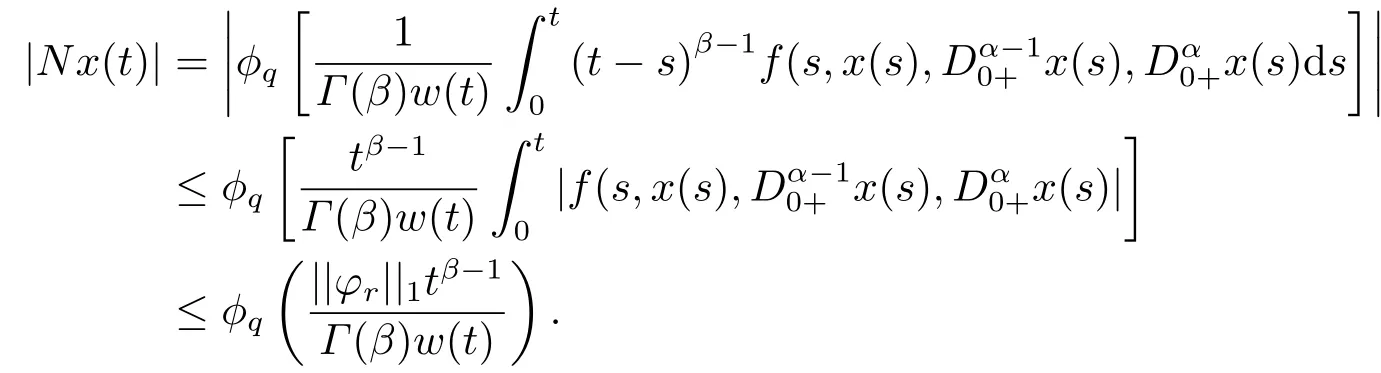
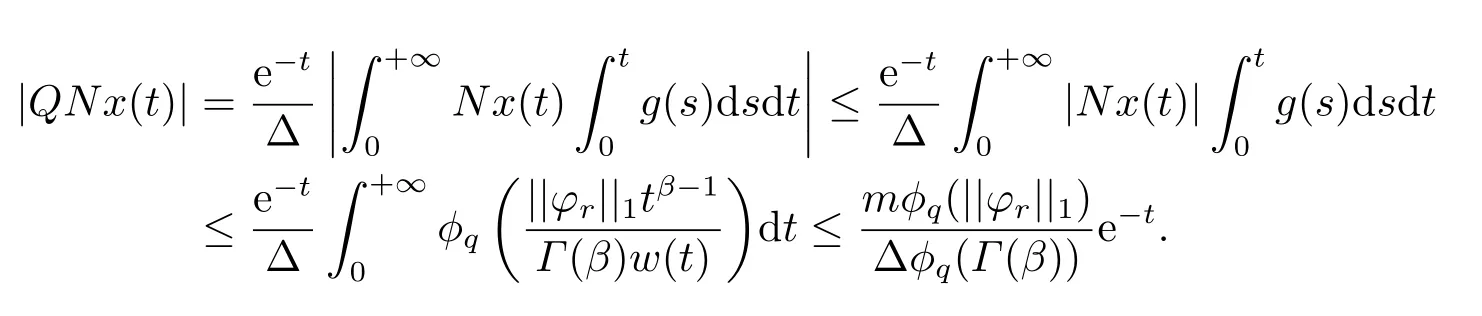
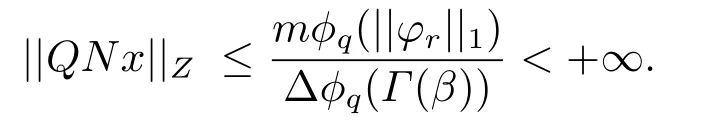
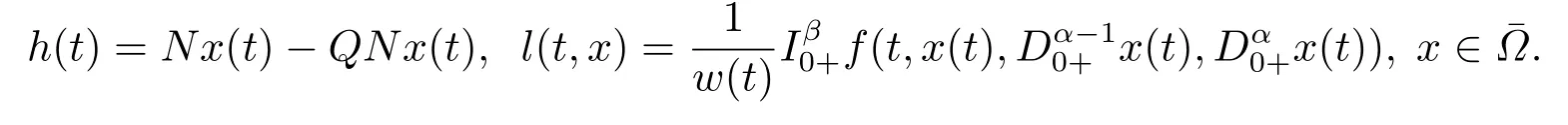

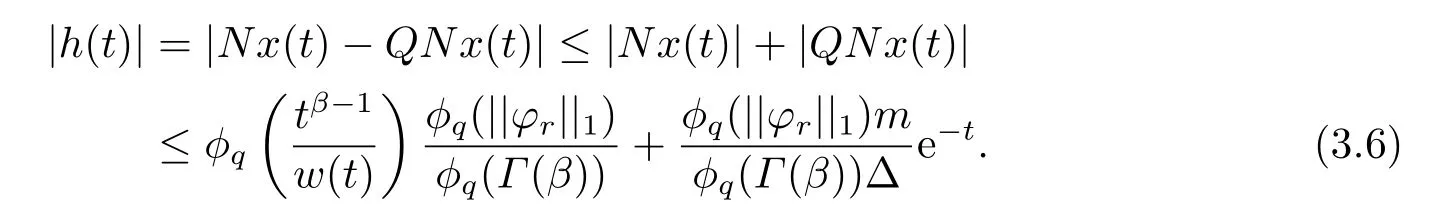
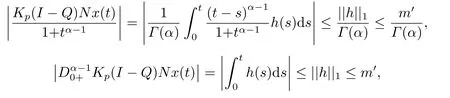
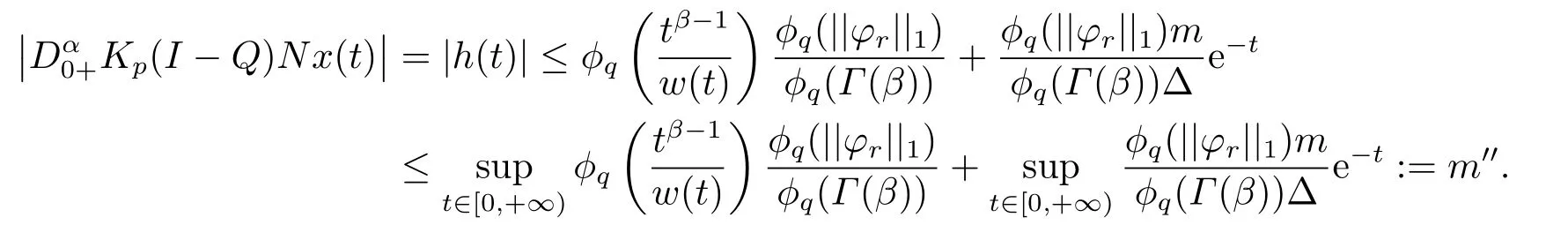
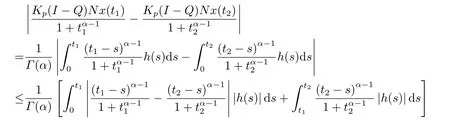
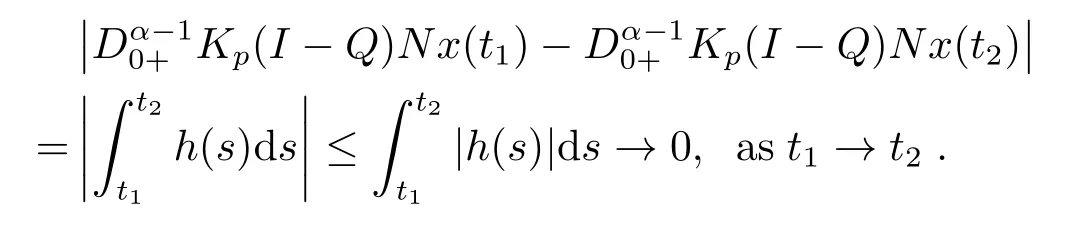
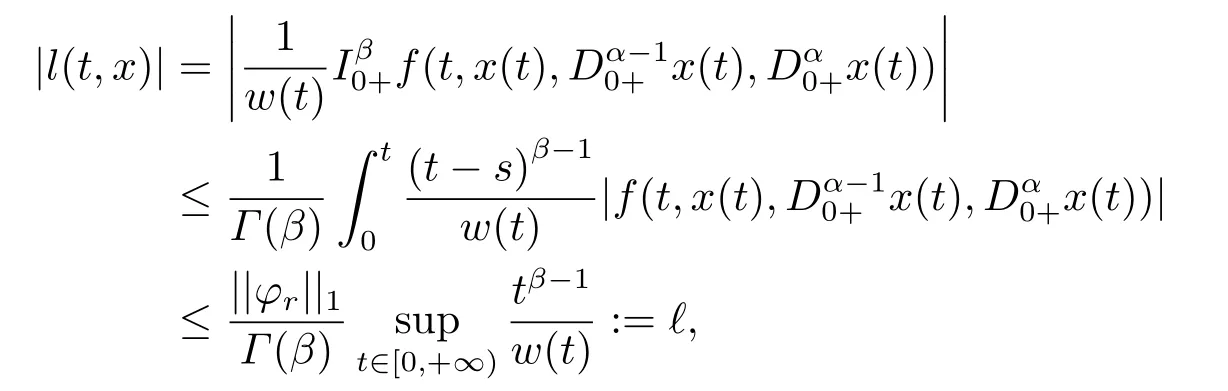
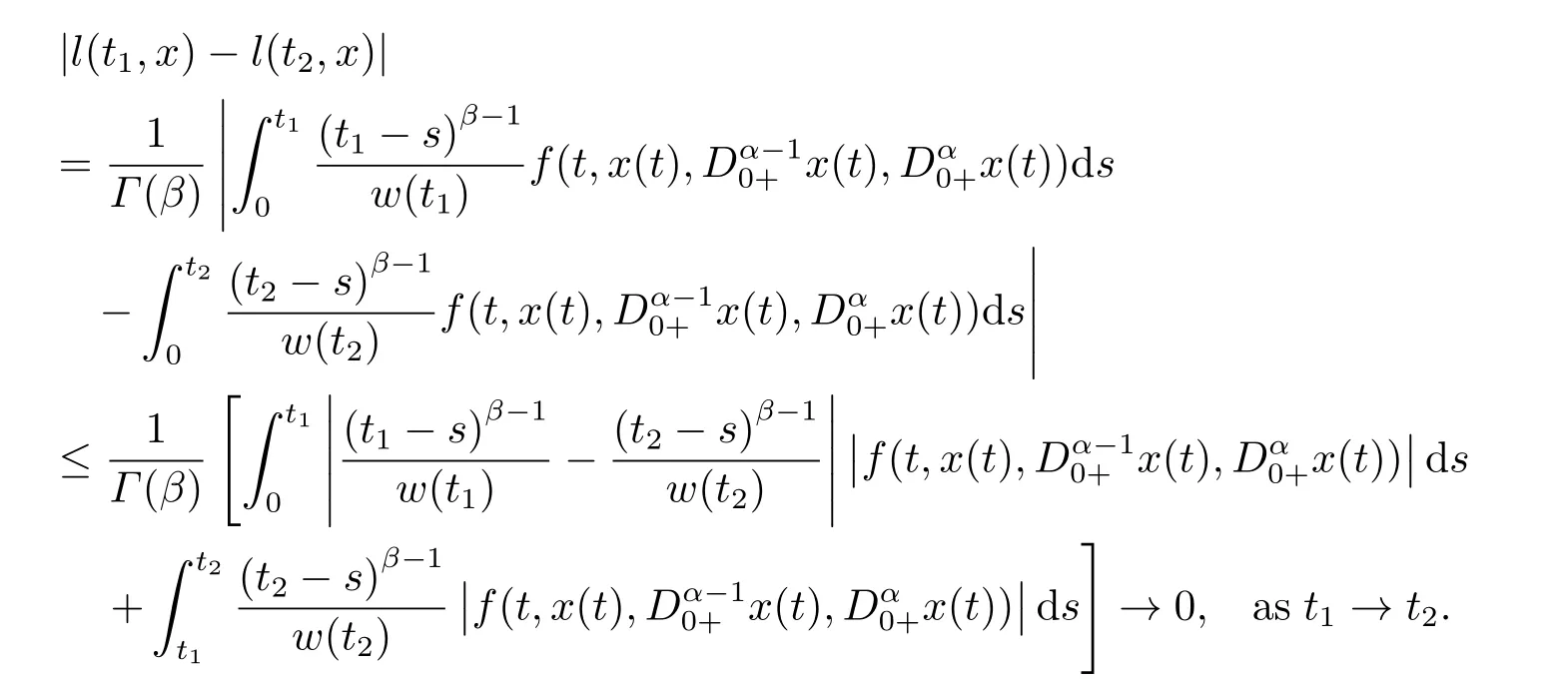
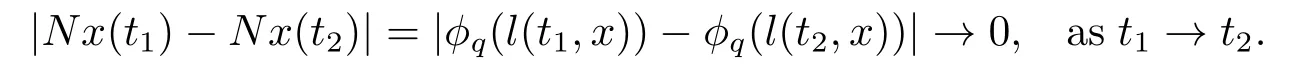
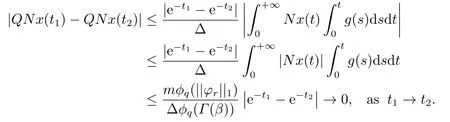

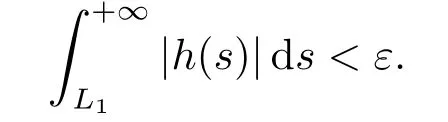
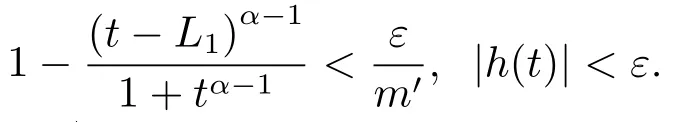
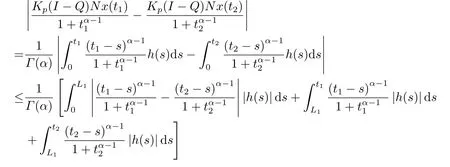
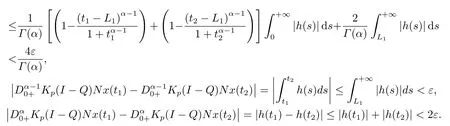
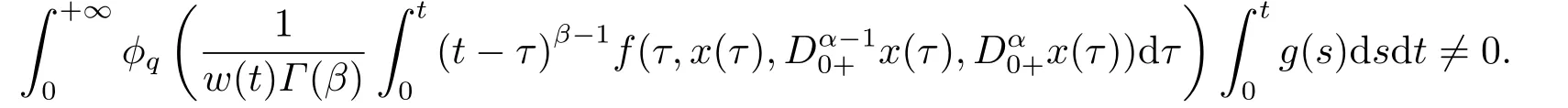
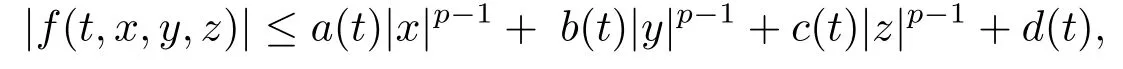

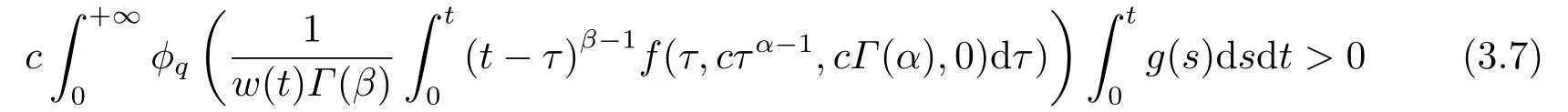
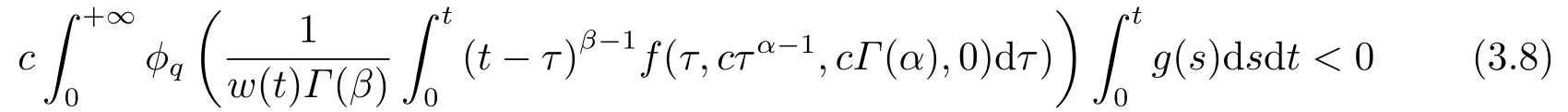
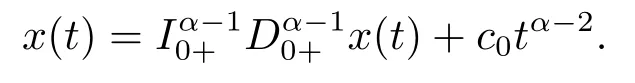


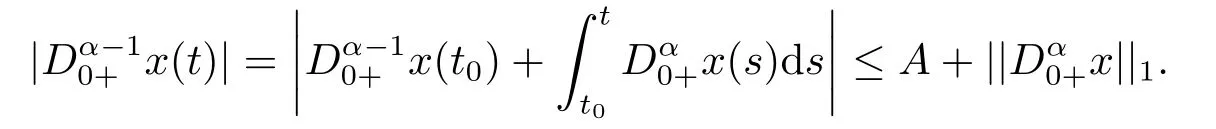
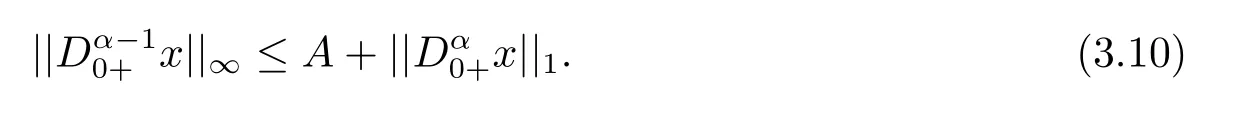
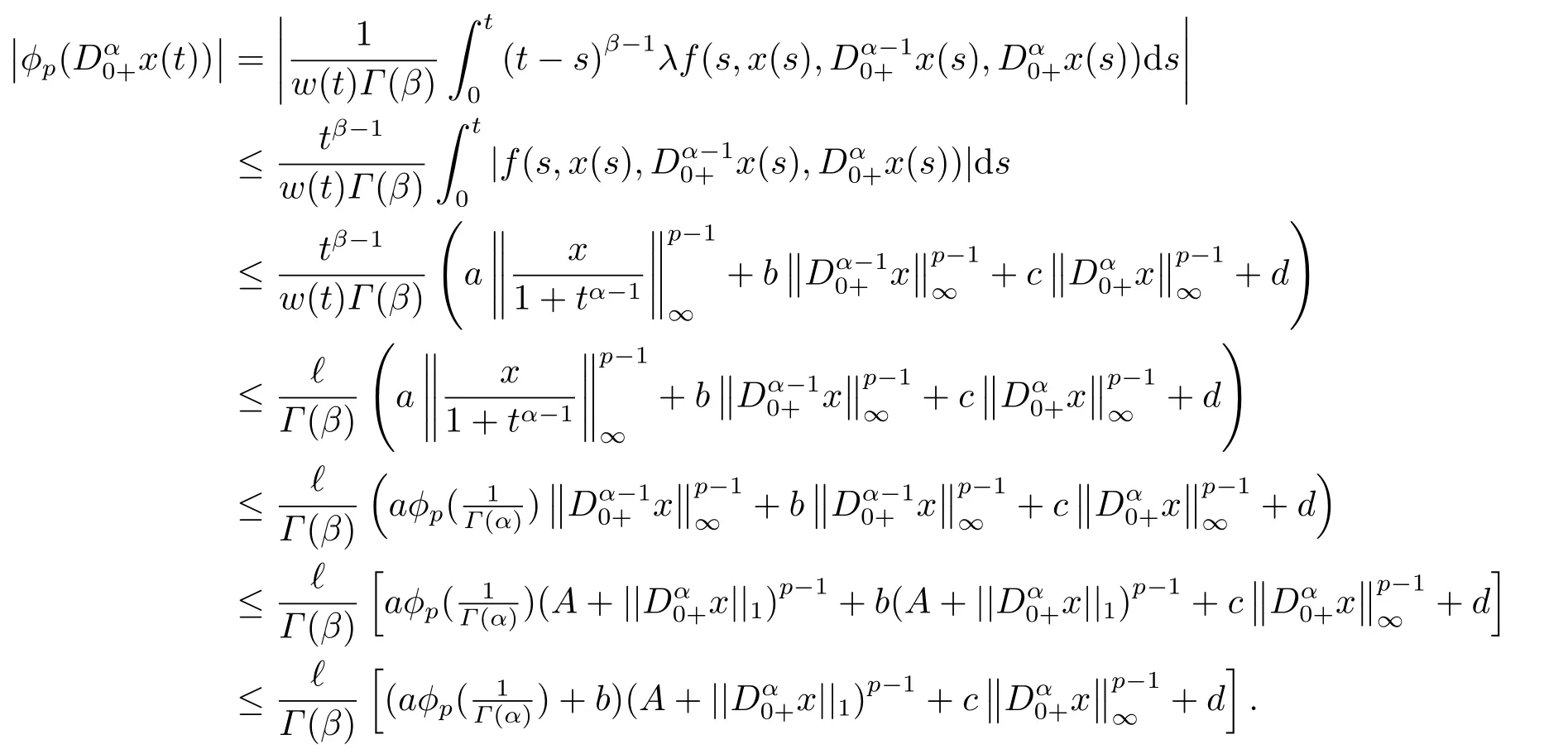

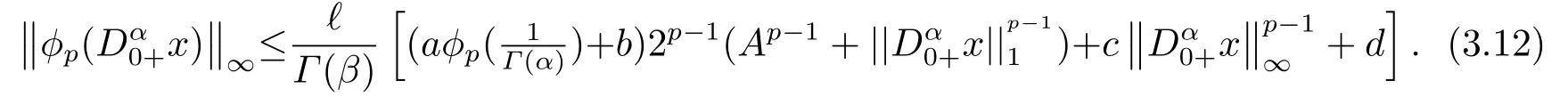
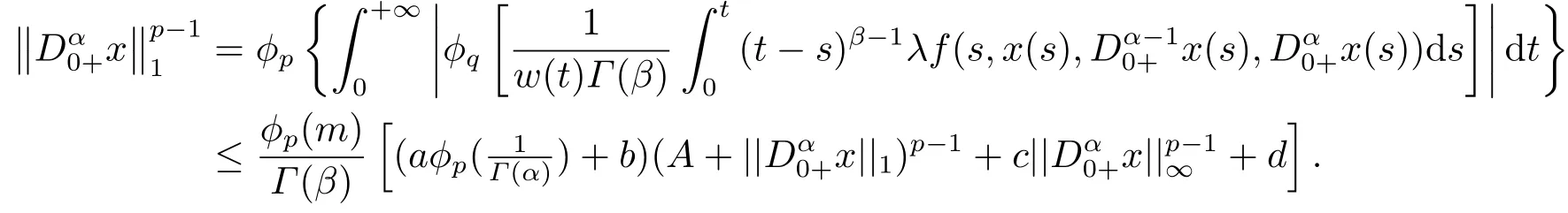

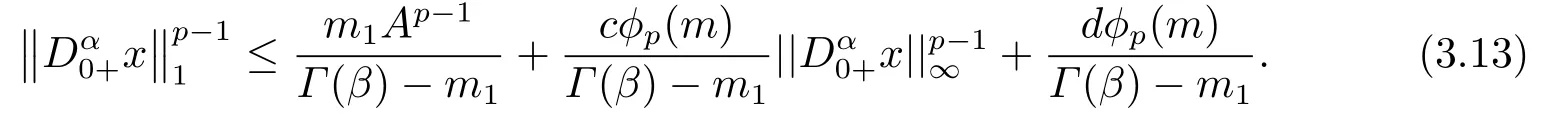
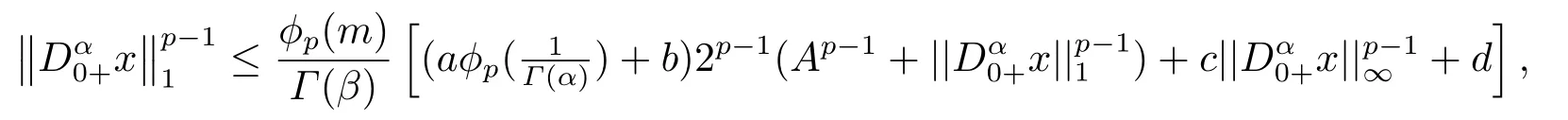

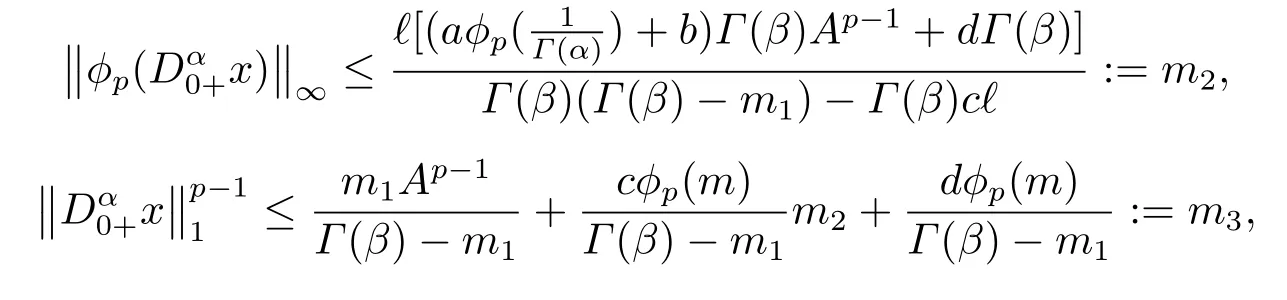
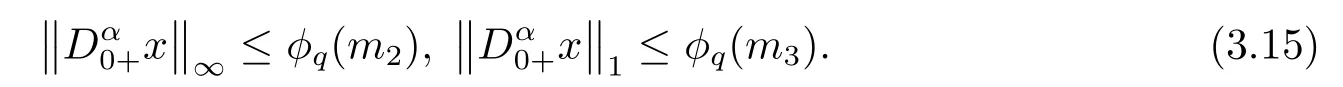
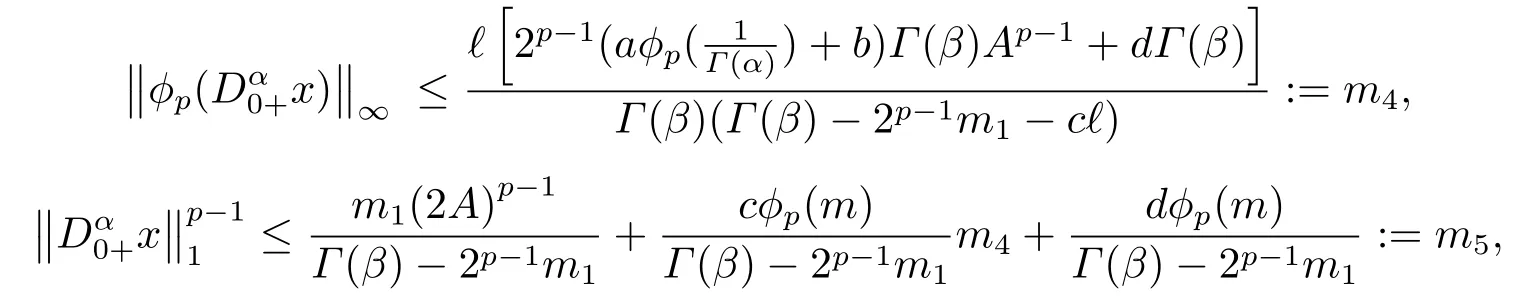
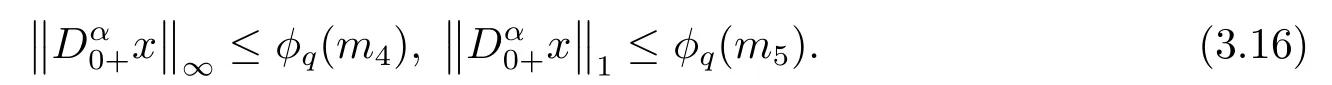
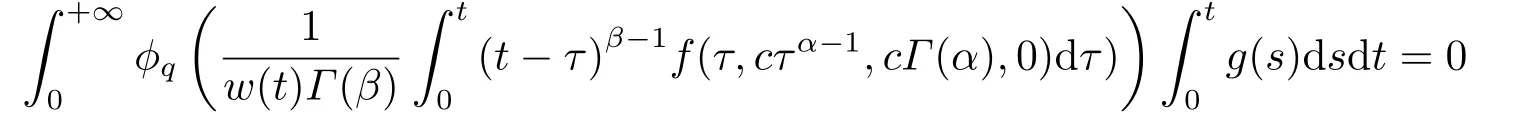
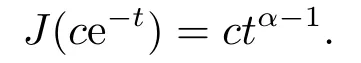

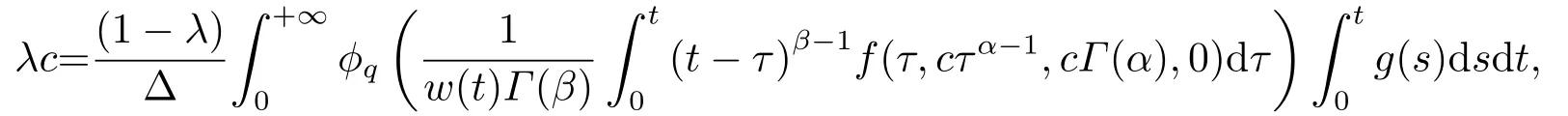
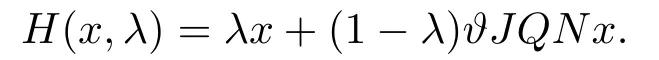
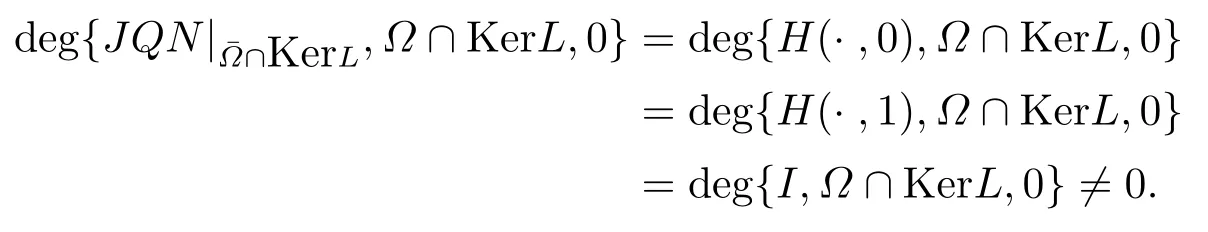
4.Example