吳亞楠,任苗苗

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

眾所周知,同余在代數(shù)的研究過程中扮演著非常重要的角色.文獻(xiàn)[1]通過類比交換環(huán)上的理想,引入了可換加法冪等元半環(huán)的素同余的概念,且完整地描述了tropical半域T,半域Zmax和二元半域B上的多項(xiàng)式半環(huán)和Laurent多項(xiàng)式半環(huán)的素同余.

定義 1.1設(shè)(S,+,·,0,1)是(2,2,0,0)型代數(shù).若S滿足下列條件:

(1)(S,+,0)是可換幺半群;

(2)(S,·,1) 是幺半群;

(3)(?a,b,c∈S)a(b+c)=ab+ac,(a+b)c=ac+bc;

(4)(?a∈S)a·0=0·a=0;

則稱S是半環(huán)[2].進(jìn)一步,若(S,·)是交換半群,則稱S是交換半環(huán).接下來給出交換半環(huán)上同余的概念.

定義 1.2設(shè)S是交換半環(huán),ρ是S×S的子集.若對(duì)于任意a,b,c,d∈S,

(1)(a,a)∈ρ;

(2)(a,b)∈ρ蘊(yùn)含著 (b,a)∈ρ;

(3)(a,b),(b,c)∈ρ蘊(yùn)含著 (a,c)∈ρ;

(4)(a,b),(c,d)∈ρ蘊(yùn)含著 (a+c,b+d)∈ρ;

(5)(a,b),(c,d)∈ρ蘊(yùn)含著 (ac,bd)∈ρ,

則稱ρ是S上的同余.

容易驗(yàn)證,{(a,a)|a∈S}是S上最小的同余.稱其為平凡同余,記為?.另一方面,S×S是S上最大的同余,稱其為S上的泛同余,記為?.若同余ρ是?的真子集,則稱ρ是S上的真同余.

定義 1.3設(shè)S是交換半環(huán).若(S,+)是冪等元半群,則稱S為可換的加法冪等元半環(huán).

分配格和max-plus代數(shù)都是可換的加法冪等元半環(huán)的例子.以下總假設(shè)S為可換的加法冪等元半環(huán).

定義 1.4設(shè)S為可換的冪等元半環(huán).在S×S上定義二元運(yùn)算如下:

(a1,a2)(b1,b2)=(a1b1+a2b2,a1b2+a2b1),

稱上述運(yùn)算為扭積運(yùn)算[1].

定義 1.5設(shè)ρ,σ是S上的同余.稱{αβ|α∈ρ,β∈σ}生成的同余為ρ和σ的積,記為ρσ[1].

引理 1.1[1]設(shè)ρ是S上的同余.若α∈ρ,β∈S×S,則αβ∈ρ.

定義 1.6設(shè)ρ是S上的真同余.若對(duì)于任意的α,β∈S×S,αβ∈ρ蘊(yùn)含著α∈ρ或β∈ρ,則稱ρ是S上的素同余[1].

定義 1.7設(shè)ρ是S上的同余.稱包含ρ的所有素同余的交是同余的根,記為[1].

引理 1.2[1]設(shè)ρ是S上的同余.則

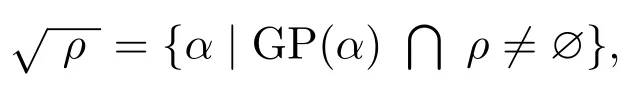
其中α=(a,b),α?=(a+b,0),GP(α)={α?k+(c,0))αl|k,l∈Z+,c∈S}.

定義 1.8設(shè)ρ是S上的同余.若,則稱ρ是根同余[1].

本文將研究可換冪等元半環(huán)的同余.給出素同余和同余的根的一些結(jié)果,且揭示了同余ρ的根與包含ρ的素同余的全體之間的關(guān)系.

2 素同余

為了方便敘述,本文將{1,2,···,n}記為.

定義 2.1設(shè)ρ是S上的真同余.若對(duì)于S上的任意同余σ,ρ?σ??蘊(yùn)含著ρ=σ或σ=?,則稱ρ是S上的極大同余.

命題 2.1每個(gè)可換的加法冪等元半環(huán)都有素同余.

證明假設(shè)Σ是S上的真同余的全體.易證 (Σ,?)是偏序集.假設(shè){ρi}i∈I是 Σ上的鏈.易知是同余.現(xiàn)證.假設(shè).則存在i∈I,使得(0,1)∈ρi.進(jìn)一步,有?∈ρi,與ρ∈Σ相矛盾,所以.運(yùn)用 Zorn引理,得 Σ有極大同余,所以S上都有極大同余.由文獻(xiàn)[1]可知S上的極大同余是素同余.證畢.

注 2.1S上的素同余對(duì)交運(yùn)算未必封閉.例如:設(shè)S={1,0,x}是可換的冪等元半環(huán),它的運(yùn)算表如下:

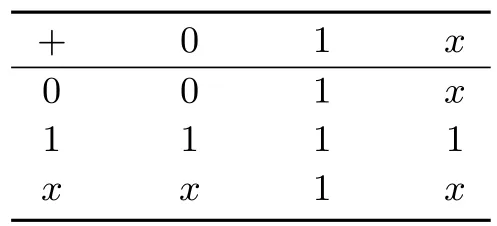
表 1 運(yùn)算 “+”

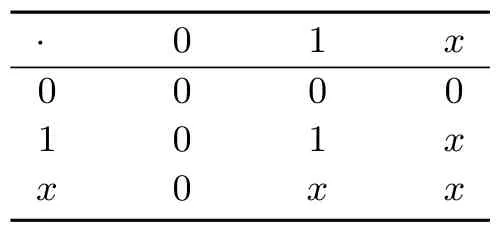
表 2 運(yùn)算 “·”

證明假設(shè)α是S×S上的冪零元.由定義2.2和引理 1.2得,存在k,l∈Z+,c∈S,使得 (α?k+(c,0))αl∈?,則 (α?k+(c,0))αl?1α∈?.由定義 2.3 可得,α是零因子.

注 2.2定理2.2的逆命題不成立.例如:設(shè)S={1,0,a,b}是可換的冪等元半環(huán),它的運(yùn)算表如下:

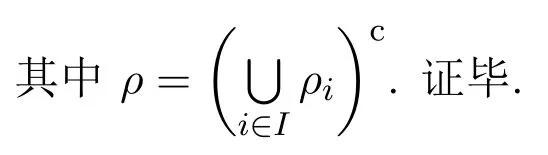
3 同余的根

致謝感謝趙憲鐘教授和邵勇教授的指導(dǎo).