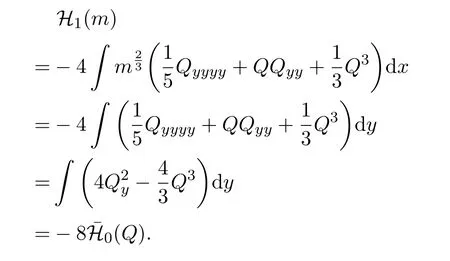康婷,郭旭,郭明月,時(shí)振華

(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)

1 引言

水波的研究是自然科學(xué)研究的一個(gè)熱點(diǎn)問(wèn)題,科學(xué)家提出許多數(shù)學(xué)模型用來(lái)描述淺水波的傳播,對(duì)于這些數(shù)學(xué)模型已經(jīng)有許多重要的結(jié)果[1-6].本文研究可積的短波模型的Novikov方程族和Sawada-Kotera方程族之間的劉維爾相關(guān)性.這兩個(gè)方程族分別源于短波模型的Novikov方程[7]

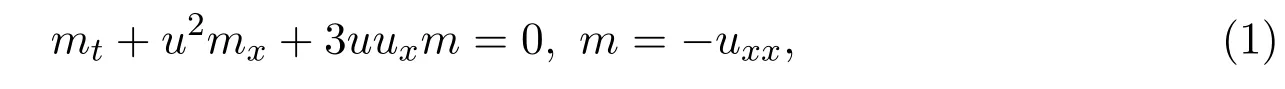
和Sawada-Kotera方程[8-9]

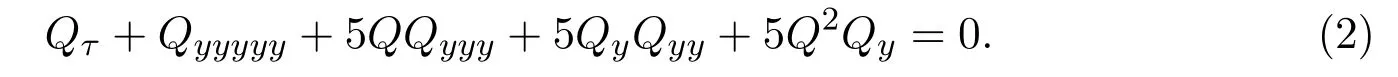
在幾何上,Sawada-Kotera方程來(lái)自仿射幾何中的可積平面曲線流[10].Sawada-Kotera方程是一種典型的五階可積方程[8],它的可積性可以從幾個(gè)不同的角度來(lái)驗(yàn)證,例如:對(duì)應(yīng) 3×3的等譜問(wèn)題,具有雙哈密頓結(jié)構(gòu)和多孤子解等.通過(guò)對(duì)包含二次非線性項(xiàng)和三次非線性項(xiàng)的Camassa-Holm型方程進(jìn)行對(duì)稱分類(lèi)[11],Novikov發(fā)現(xiàn)具有三次非線性項(xiàng)的偏微分方程mt+u2mx+3uuxm=0,m=u?uxx.隨后,文獻(xiàn)[12]證明Novikov方程具有Lax對(duì)和雙哈密頓結(jié)構(gòu),并且通過(guò)一個(gè)互反變換將其與負(fù)的Sawada-Kotera方程聯(lián)系起來(lái).在此基礎(chǔ)上,文獻(xiàn)[12]對(duì) Novikov方程族和Sawada-Kotera方程族進(jìn)行詳細(xì)的研究.之后,文獻(xiàn)[7]提出短波模型的Novikov方程(1)是三階可積方程.并且,Li在2018年通過(guò)等譜問(wèn)題之間的互反變換將短波模型的Novikov方程與負(fù)的Sawada-Kotera方程聯(lián)系起來(lái).參考文獻(xiàn)[13-16],本文將研究短波模型的Novikov方程族與Sawada-Kotera方程族中每一對(duì)方程和每一對(duì)哈密頓守恒律之間的劉維爾對(duì)應(yīng)關(guān)系.

本文的提綱如下:在第2節(jié)中,介紹短波模型的Novikov與Sawada-Kotera方程等譜問(wèn)題之間的劉維爾變換;在第3節(jié)中,利用劉維爾變換發(fā)現(xiàn)兩個(gè)方程族中方程的一一對(duì)應(yīng)關(guān)系;在第4節(jié)中,建立方程族哈密頓守恒律之間的一一對(duì)應(yīng)關(guān)系.

2 短波模型的Novikov與Sawada-Kotera方程譜問(wèn)題之間的劉維爾變換

在本節(jié)中,通過(guò)等譜問(wèn)題之間的互反變換,得到短波模型的 Novikov方程族與Sawada-Kotera方程族之間的劉維爾變換.劉維爾變換是由變量的變化來(lái)描述一個(gè)光譜問(wèn)題與另一個(gè)光譜問(wèn)題的關(guān)系[17-18],其中獨(dú)立變量的變換是互反變換.如果變換不影響?yīng)毩⒆兞?則稱為Miura變換.

短波模型的Novikov方程

3 短波模型的Novikov方程族與Sawada-Kotera方程族之間的對(duì)應(yīng)關(guān)系

本節(jié)考慮短波模型的Novikov方程族與Sawada-Kotera方程族中每一對(duì)可積方程之間的對(duì)應(yīng)關(guān)系.短波模型的Novikov方程(3)可以寫(xiě)成雙哈密頓形式

是兩個(gè)相容的哈密頓算子,對(duì)應(yīng)的哈密頓泛函為

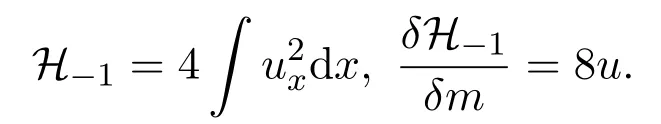
根據(jù)Magri理論[19-20],對(duì)于一個(gè)具有相容哈密頓算子K和J的可積雙哈密頓系統(tǒng),R=KJ?1為其允許的遞推算子.將遞推算子迭代作用在種子對(duì)稱上即可生成該雙哈密頓系統(tǒng)對(duì)應(yīng)的擁有無(wú)窮多個(gè)可積方程的可積方程族,其中每一個(gè)方程都是以K和J為相容哈密頓算子的雙哈密頓系統(tǒng).具體地,對(duì)于短波模型的Novikov方程,將遞推算子R=KJ?1迭代作用到種子對(duì)稱mt=mx,即可得相應(yīng)可積方程族.其正族第l個(gè)方程的雙哈密頓形式為

4 短波模型的Novikov方程族與Sawada-Kotera方程族哈密頓守恒律之間的對(duì)應(yīng)關(guān)系

根據(jù)Magri理論,對(duì)于一個(gè)雙哈密頓系統(tǒng),由其允許的一對(duì)相容哈密頓算子,可以遞推地構(gòu)造雙哈密頓系統(tǒng)允許的無(wú)窮多個(gè)守恒律.特別地,對(duì)于短波模型的Novikov方程族,哈密頓守恒律Hl滿足遞推公式

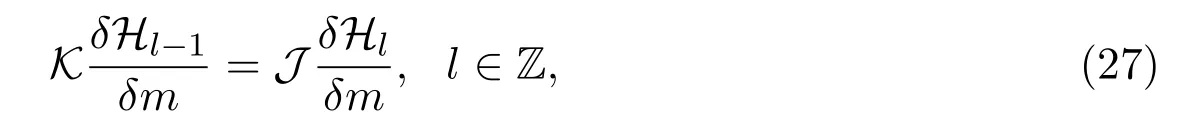
其中K和J是兩個(gè)相容的哈密頓算子(13).另一方面,Sawada-Kotera方程族哈密頓守恒律l滿足遞推公式

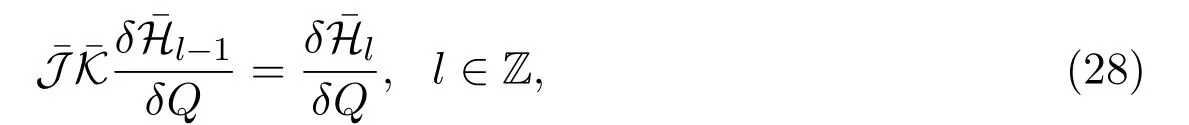
引理4.1設(shè)Hl和l是分別由遞推公式(27)和公式(28)確定的哈密頓泛函族.對(duì)任意整數(shù)l,其相應(yīng)的變分導(dǎo)數(shù)滿足關(guān)系

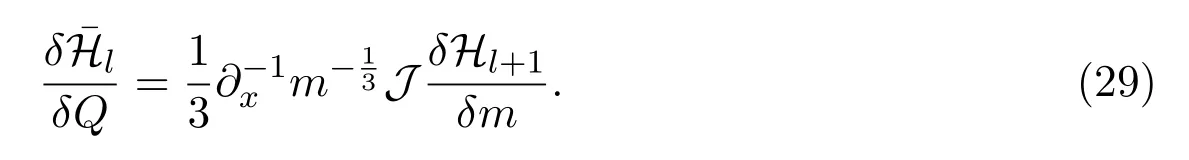
證明(i)l是非負(fù)整數(shù)