陳巧琳, 尤 澤, 李保軍

(成都信息工程大學(xué)應(yīng)用數(shù)學(xué)學(xué)院, 成都 610025)

定義1[2]設(shè)F為一個群類, 如果對G的任意元素x和任意F-離中心主因子H/K,x在H/K上誘導(dǎo)一個內(nèi)自同構(gòu), 則群G稱為一個擬F-群．

設(shè)F為一個飽和群系, 則一個F-群的所有主因子都是F-中心的, 因此一個F-群一定是擬F-群, 但反之不然．本文所討論的群類F皆為飽和群系, 并用符號F*表示所有擬F-群的群類．如果存在G的子群T∈F*且G=HT, 則G的子群H稱為有擬F-補充．

定義2[5]如果|(G/K)∶CG/K((H∩L)K/K)|是一個π((H∩L)K/K)-數(shù), 則子群H稱為在G中有Π-性質(zhì)．設(shè)G的一個子群T在G中有一個補充X, 使得X次正規(guī)于G且T∩X≤I≤T, 其中I為G的某個有Π-性質(zhì)的子群, 則稱T在G中是Π-正規(guī)的．

文獻(xiàn)[5]利用子群的Π-性質(zhì)和Π-正規(guī)性獲得了一系列好的研究成果, 其工作受到廣泛關(guān)注[6-10]．本文擬借助子群的Π-正規(guī)性研究群的結(jié)構(gòu), 并給出擬F-群的一些新判別方法．

1 預(yù)備知識

對于擬冪零群,容易證明:

性質(zhì)3G為擬p-冪零群當(dāng)且僅當(dāng)G/Op′(G)為擬冪零群．

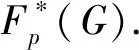
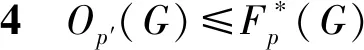
引理5[5]設(shè)H為G的一個子群,N為G的一個正規(guī)子群, 則

1) 如果H在G中有Π-性質(zhì), 則HN/N在G/N中有Π-性質(zhì);

2) 如果H在G中有Π-性質(zhì), 則H在G中是Π-正規(guī)的;

3) 如果H在G中是Π-正規(guī)的且N?H或(|N|,|H|)=1, 則HN/N在G/N中是Π-正規(guī)的．

引理6[5]設(shè)H為群G的一個p-子群,L為G的一個極小正規(guī)子群．如果H∩L≠1且H在G中是Π-正規(guī)的, 則L為p-群．

引理7[5]設(shè)H為群G的一個p-子群且N為G的一個極小正規(guī)子群．如果H正規(guī)于G的某個Sylowp-子群且H在G中是Π-正規(guī)的, 則H∩N=N或1．

引理8[10]設(shè)K為群G的一個正規(guī)子群且G/K∈F, 其中F為任意飽和群系．若K的所有p階和4階(當(dāng)p=2且K的Sylow 2-子群非交換)元素皆含于G的F-超中心, 則G/Op′(G)∈F．

如果對任意群G和它的一個可解正規(guī)子群N滿足: 當(dāng)G/Φ(N)∈X時,G∈X, 則群系X稱為可解飽和的．

引理9[3]設(shè)F為包含冪零群系的一個飽和群系, 則F*為可解飽和群系．

引理10[11]設(shè)群Q穩(wěn)定作用在p-群P上, 則[P,Op(Q)]=1．

2 主要結(jié)論

證明 假設(shè)定理不成立．設(shè)G為極小階反例,可通過以下步驟完成定理證明:

(1)Op′(N)=1, 容易驗證, 條件對(G/Op′(N),N/Op′(N))仍成立．若Op′(N)≠1, 則由G的選擇可知G/Op'(N)為擬F-群; 由F包含所有p-冪零群知, 所有p′-主因子都是F-中心的, 故G為擬F-群, 矛盾于G的選擇, 從而(1)成立．

(3)Op(N)≤Z∞(G)．欲證Op(N)≤Z∞(G), 只要證明N的所有G-不變子群P皆含于Z∞(G)．設(shè)L為含于P的任意G-不變子群, 則由對|P|的歸納, 有L≤Z∞(G)．設(shè)PZ∞(G)并令L為所有真含于P的G-不變子群的乘積,L≤Z∞(G)且P/L為G的主因子．若P/L循環(huán), 則|P/L|=p且G/CG(P/L)為方次數(shù)整除p-1的交換群．由(|G|,p-1)=1, 得G/CG(P/L)=1, 即P/L為中心主因子, 又L≤Z∞(G), 故P≤Z∞(G)．設(shè)P/L非循環(huán), 令C=CG(L)．由引理10知Op(G)≤C, 顯然CG, 則P∩LC=L(P∩C)G．由P/L為G的主因子, 得P∩LC=L或P．若P∩LC=L, 則P∩C≤L, 故[P,C]≤L．于是C平凡作用在P/L上, 即G/CG(P/L)為p-群．另一方面,G/CG(P/L)為p′-群, 則G/CG(P/L)=1,P≤Z∞(G)．設(shè)P∩LC=P,有P∩CL．由L的選擇可知P∩C=P, 即L≤Z(P)．令a,b為P的任意2個p階元, 若p≠2或P交換, 則(ab)p=apbp[a,b]p(p-1)/2=1, 故Ω={a|ap=1}為P的1個特征子群．若Ω≤L, 由引理10 以及Op(G)≤C,Op(G)平凡作用在P上, 有G/CG(P/L)=1,P≤Z∞(G)．設(shè)Ω=P, 則P的所有元素皆為p階．令H/L≤Z(Gp/L∩P/L)為p階群, 其中Gp為G的一個Sylowp-子群, 取x∈HL, 則H=〈x〉L且〈x〉為p階群．設(shè)〈x〉在G中有擬F-補充T, 由L≤Z∞(G)且F包含所有p-冪零群可知TL仍為擬F-群．不妨設(shè)T=TL, 即L≤T, 若T=G,則G為擬F-群, 矛盾. 故T

(5) 由步驟(3)(4)得N≤Z∞(G), 而G/N∈F*, 故G∈F*, 矛盾, 證畢．

引理12設(shè)p為群G的階的素因子且(|G|,p-1)=1,X為G的一個正規(guī)子群, 若X的Sylowp-子群的所有極大子群在G中Π-正規(guī), 則X為p-冪零群．

引理13設(shè)p為群G階的素因子且(|G|,p-1)=1,P為G的一個正規(guī)p-子群．若P的所有極大子群在G中Π-正規(guī), 則X≤Z∞(G)．

證明 設(shè)定理不成立并設(shè)G為極小階反例, 則:

(1)Op′(N)=1, 容易驗證條件對(G/Op′(N),N/Op′(N))仍成立．設(shè)Op′(N)≠1,則由G的選擇知G/Op'(N)為擬F-群, 故G為擬F-群,與G的選擇矛盾, (1)成立．

(2)X為p-群且X≤Z∞(G)．由引理12知X為p-冪零群,又Op′(X)≤Op′(N)=1, 故X為p-群．由引理13知X≤Z∞(G)成立．