牛瀟萌

(赤峰學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,內(nèi)蒙古 赤峰 024000)

1 引言

設(shè)f(z)與g(z)在U={z:|z|<1}內(nèi)解析,如果存在U內(nèi)滿足|ω(z)|≤|z|的解析函數(shù)ω(z),使得f(z)=g(ω(z)),則稱f(z)從屬于g(z),記作f(z)?g(z).特別地,如果g(z)在U上是單葉的,則

的全體.顯然P(C,D)?P(1,?1)=P,P為熟知的正實(shí)部函數(shù)類.

設(shè)S表示在單位圓盤U內(nèi)單葉解析函數(shù)

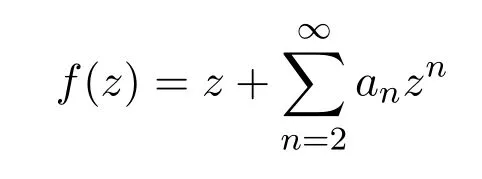
構(gòu)成的函數(shù)類.S?,C和Bα分別表示通常的星象函數(shù)類,近于凸函數(shù)類和Bazilevi?函數(shù)類,它們都是S的子類且S??C?Bα.

用G表示復(fù)平面上包含原點(diǎn)的區(qū)域,稱G是圓對(duì)稱區(qū)域,如果對(duì)每個(gè)R∈(0,∞),G∩{|z|=R}或是空集,或是整個(gè)圓周{|z|=R},或是包含z=R且關(guān)于實(shí)軸對(duì)稱的圓周G∩{|z|=R}上的一段圓弧.設(shè)f∈S,若函數(shù)f(z)將U映射為圓對(duì)稱區(qū)域G,則稱f(z)屬于圓對(duì)稱函數(shù)類Y[1].設(shè)α>0,β∈R,f(z)∈S,如果存在g(z)∈S?使

的全體組成的函數(shù)類.稱Dn(λ)為Milin系數(shù).

研究 Milin系數(shù)和相鄰兩系數(shù)模之差||Dn+1(λ)|?|Dn(λ)||是單葉函數(shù)論中兩個(gè)重要問題.近些年來,許多作者研究了單葉函數(shù)中一些特殊函數(shù)族的Milin系數(shù)和相鄰兩系數(shù)模之差的估計(jì).如文獻(xiàn)[4-9]分別引入了一些特殊解析函數(shù)類,并討論了其Milin系數(shù)和相鄰兩系數(shù)模之差的估計(jì).首先,文獻(xiàn)[9]給出了當(dāng)時(shí),S上|Dn(λ)|準(zhǔn)確的階,但當(dāng)時(shí),只獲得了

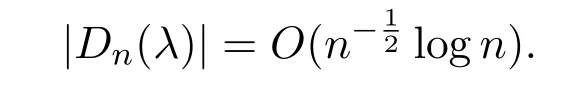
文獻(xiàn)[8]繼續(xù)討論幾類特殊單葉函數(shù)類(S?,C,Y和Bα)上Milin系數(shù)|Dn(λ)|階的估計(jì),得到如下結(jié)果:

定理 1.1設(shè)f(z)∈Bα,Dn(λ)由 (2)式定義,則

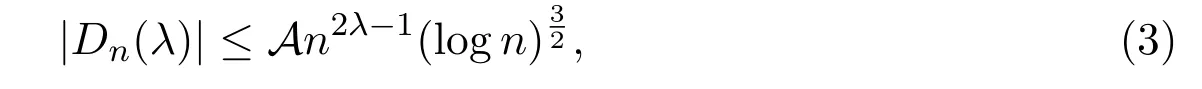
其中A是絕對(duì)常數(shù),指數(shù)2λ?1是最佳的.

本文進(jìn)一步對(duì)f(z)∈Bα,β(C,D)時(shí),估計(jì)系數(shù)|Dn(λ)|的階,推廣了上述結(jié)果.

2 主要結(jié)果