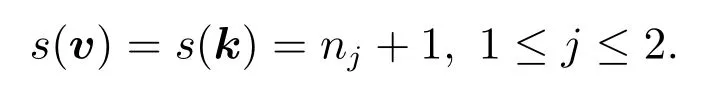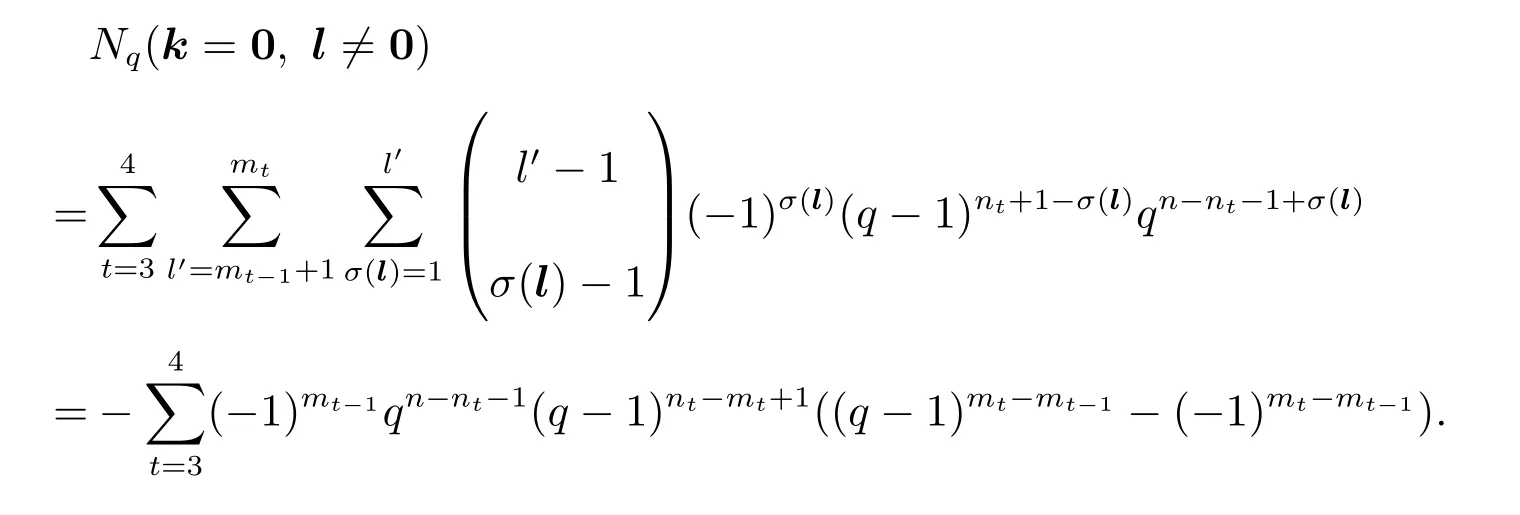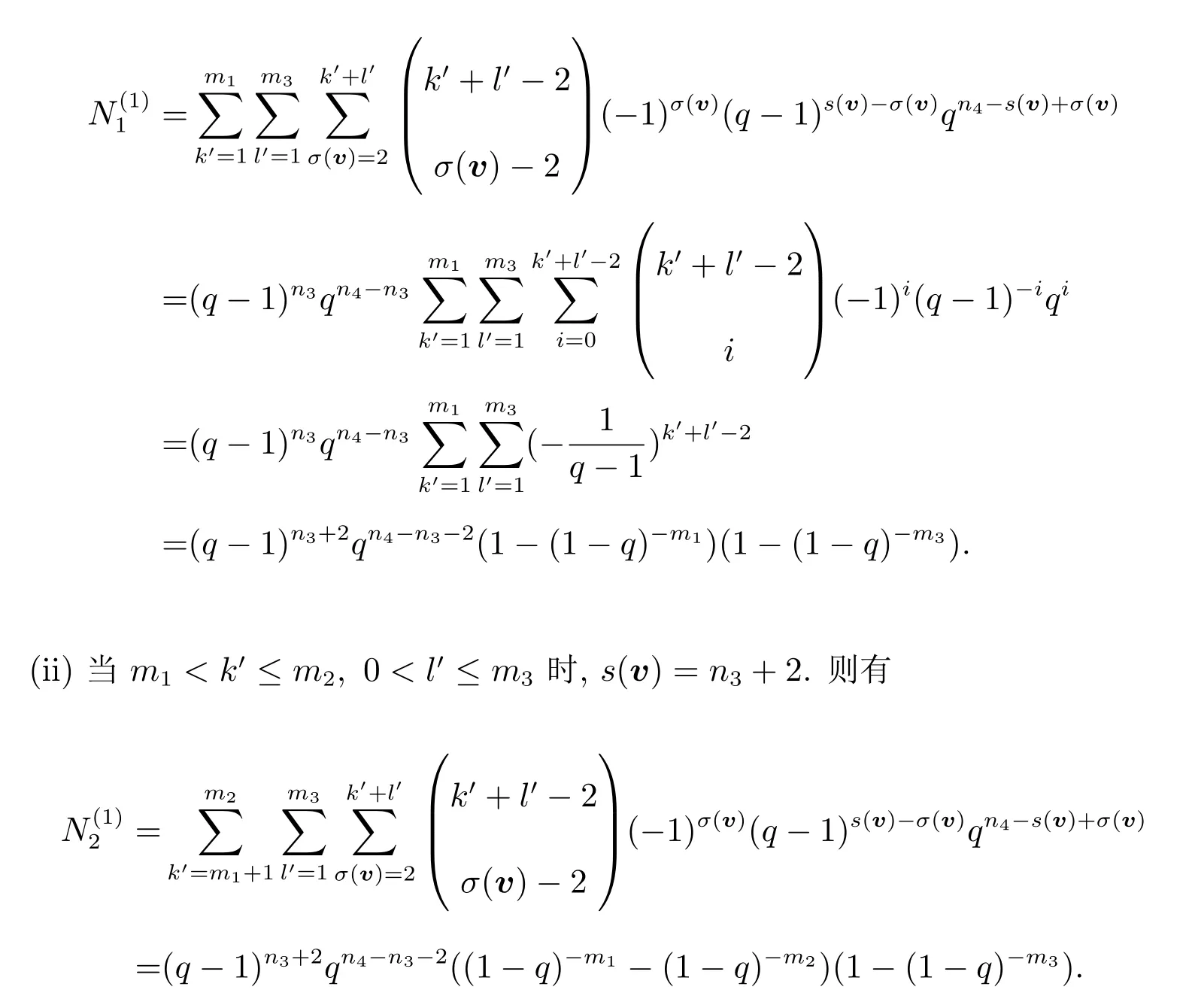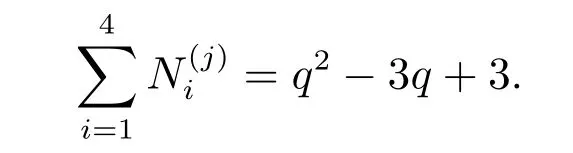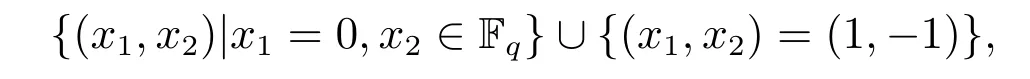由兩個多項式確定的代數(shù)簇上的有理點
高偉,黃華,曹煒
(寧波大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,浙江 寧波 315211)
1 引言
本文用 N和 N0分別表示正整數(shù)集與非負整數(shù)集.設(shè) Fq是q元有限域,其中q=pr,p為素數(shù),r∈N.用表示由 Fq中非零元構(gòu)成的乘法群.設(shè)n,t∈N,fi(X)(i=1,···,t)為 Fq上的n元多項式,V表示由多項式組f1(X),···,ft(X)所確定的代數(shù)簇.令

即Nq(V)表示代數(shù)簇V中Fq-有理點的個數(shù);特別地,如果V由單個多項式f(X)所確定(即t=1),則記Nq(f):=Nq(V).計算Nq(V)是有限域研究 (參見文獻[1-8])中的重要課題,但通常也是困難的.
文獻[3]考慮了由如下單個多項式所確定的代數(shù)簇

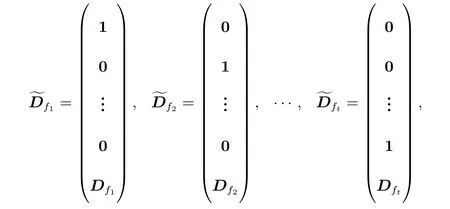
其中 0 定理 1.1[3]設(shè)f為形如 (1)的多項式.若Df是列滿秩的且其最大不變因子與q?1互素,則有 本文將研究由兩個多項式所確定的代數(shù)簇.下面將總是用W表示由下面兩個Fq上的多項式所確定的代數(shù)簇 當W的增廣次數(shù)矩陣的最大不變因子與q?1互素時,將給出代數(shù)簇W上Fq-有理點個數(shù)的具體表達式. 定義 2.2設(shè)M∈Zn×n是整數(shù)陣.若M的行列式為±1,則稱M是幺模的.整數(shù)環(huán)Z上所有n階幺模陣關(guān)于矩陣乘法構(gòu)成群,用GLn(Z)表示. 設(shè)矩陣A∈Zn×m的秩為s,則存在U∈GLn(Z)和V∈GLm(Z)使得 記對角元λi:=λii,則有:(1)λi>0,λi|λi+1,其中i=1,···,s?1,λs>0;(2)λ1···λi等于A的所有i×i階子行列式的最大公因子,其中i=1,···,s.矩陣 (λij)n×m稱作A的Smith標準形,其中對角元λi(1≤i≤s)稱作A的第i個不變因子. 如上節(jié)所述,設(shè)代數(shù)簇V由 Fq上的n元多項式組f1(X),···,ft(X)所確定,并記 其中 1:=(1,···,1),0:=(0,···,0),即fi的前t行除了第i行的元素全為 1,其它行均為零行向量.定義V的增廣次數(shù)矩陣為V=(f1,···,Dft),并設(shè)V∈Z(n+t)×m. 用σ(k)和s(k)分別表示 (k1,···,km)和 (l1,···,ln+t)中的非零元的個數(shù).即 文獻[1]利用高斯和證明了以下引理. 引理 2.1[1]設(shè)V∈Z(n+t)×m,其中m≤n+t.設(shè)V的 Smith標準形的對角元為λ1,···,λm,其中λi|λi+1,i=1,···,m?1,λm>0.若 gcd(λm,q?1)=1,則有R={0,q?1}且 設(shè)代數(shù)簇W由多項式組(2)所確定,則W的增廣次數(shù)矩陣為.假設(shè)W的最大不變因子λ滿足(λ,q?1)=1.令n=max{n2,n4}及R={0,q?1}.由引理2.1知, 下面分(a)-(d)四種情形進行討論: (a)k=0,l=0.此時顯然有Nq(k=0,l=0)=qn. (b)k0,l=0.設(shè)mj?1 為方便計,定義m1?1=0,m2?1=m1.因而有 (c)k=00.若mj?1 (d)k0,l0.對固定的k′≥1 和l′≥1,σ(v) 的取值可從 2 到k′+l′.注意到n1 (i)當 0 沿用上面討論中的定義與記號,本文的主要定理可敘述如下: 定理 3.1設(shè)代數(shù)簇W由多項式組(2)所確定.設(shè)W的最大不變因子與q?1互素.若n1,n2,n3,n4按大小順序排列屬dj(1≤j≤3)情形,則W上Fq-有理點的個數(shù)為 最后舉例說明如何應(yīng)用定理3.1. 設(shè)代數(shù)簇W由Fq上的兩個多項式 由定理3.1知,Nq(W)=q+1.另一方面,由因式分解易知方程組g1(X)=g2(X)=0的解集為 亦可得Nq(W)=q+1.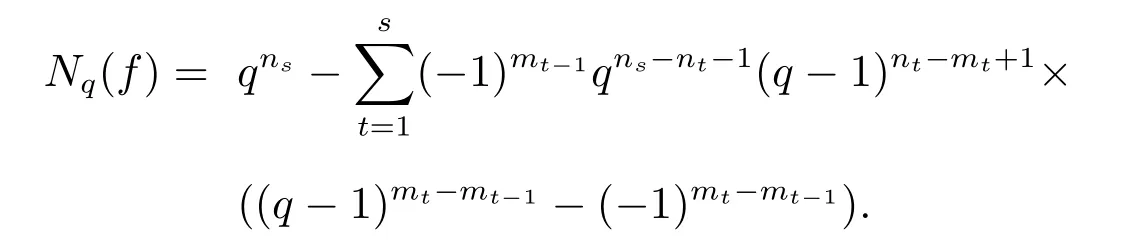
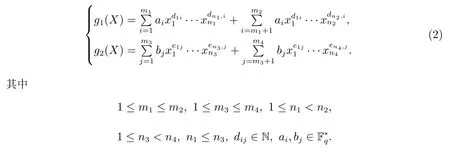
2 次數(shù)矩陣及其不變因子
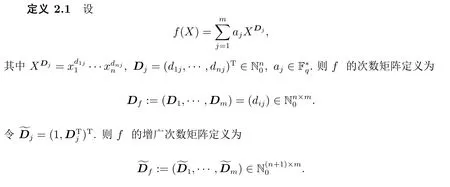

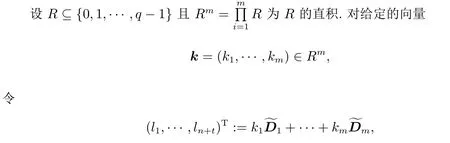
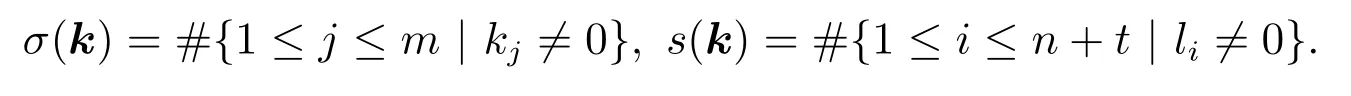

3 主要結(jié)論