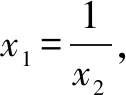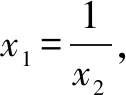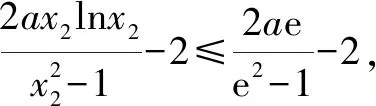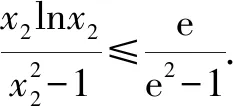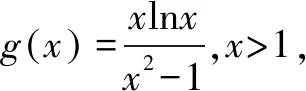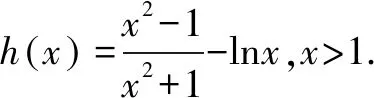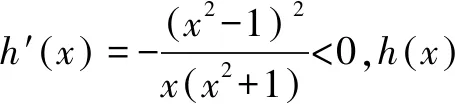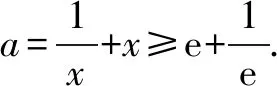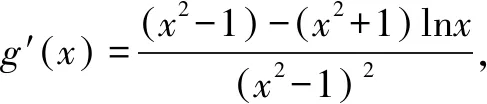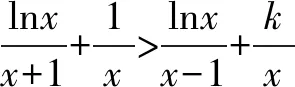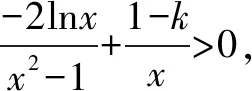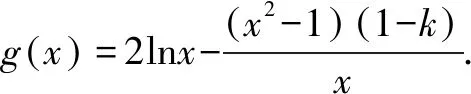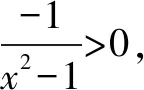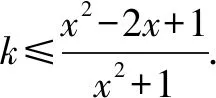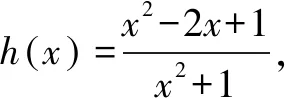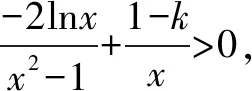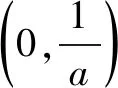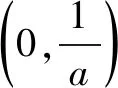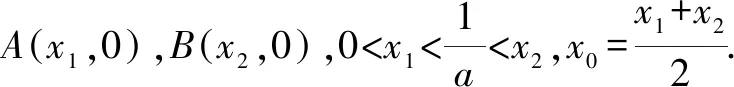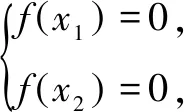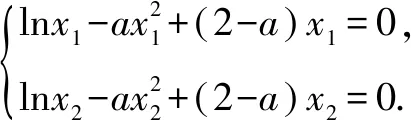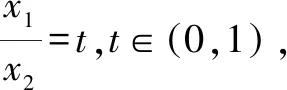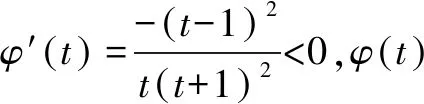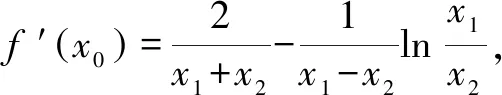蘇藝偉

(福建省龍海第一中學(xué)新校區(qū) 363100)

對于F(x)=φ(x)lnx+φ(x)之類的導(dǎo)數(shù)綜合問題,目標函數(shù)的構(gòu)造,調(diào)控,提煉乃至優(yōu)化是最佳的解決手段. 如果能夠?qū)nx前面的φ(x)分離出去,再研究剩下的函數(shù),往往可以柳暗花明,事半功倍.

例1 已知f(x)=-2(x+a)lnx+x2-2ax-2a2+a,a>0.(1)設(shè)g(x)是f(x)的導(dǎo)函數(shù),討論g(x)的單調(diào)性.(略)(2)證明:存在a∈(0,1),使得f(x)≥0在區(qū)間(1,+)內(nèi)恒成立,且f(x)=0在(1,+)內(nèi)有唯一解.

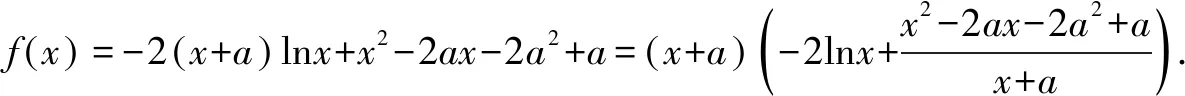
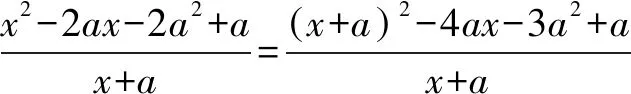
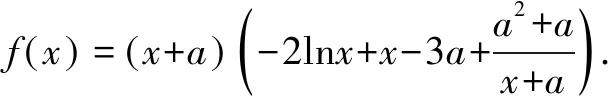
由于a∈(0,1),x∈(1,+),所以x+a>0.

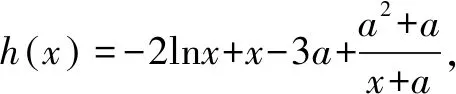
令h′(x)=0,得x2-2x-a=0.

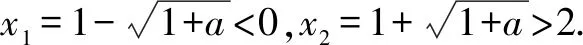
故h(x)在(1,x2)單調(diào)遞減,在(x2,+)單調(diào)遞增.

所以h(x)min=h(x2).

問題轉(zhuǎn)化為證明存在a∈(0,1),使得h(x2)=0在區(qū)間(1,+)內(nèi)存在唯一實根.

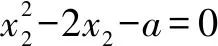
代入上式得

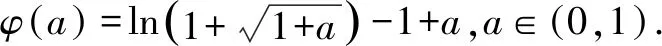
顯然φ(a)在(0,1)單調(diào)遞增,φ(0)<0,φ(1)>0.

由零點存在定理可知,存在唯一的零點x0∈(0,1),使得φ(x0)=0.

故存在a∈(0,1),使得h(x2)=0在區(qū)間(1,+)內(nèi)存在唯一實根.

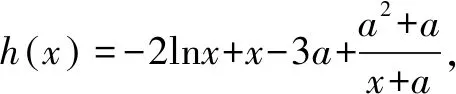
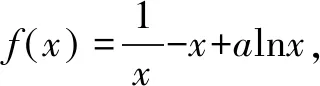
(1)若f(x)在定義域上不單調(diào),求實數(shù)a的取值范圍.(略)

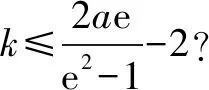
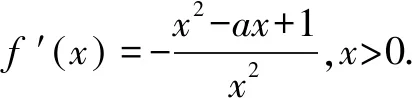
由已知有x1,x2是方程x2-ax+1=0的兩個不等正實根.故x1+x2=a,x1x2=1.

不妨設(shè)01,0

所以g′(x)<0,g(x)在(1,+)單調(diào)遞減.

故有當(dāng)00,當(dāng)x>1時,g(x)<0.

由于g(1)=0,因此有g(shù)′(x)≤0.

即k≤0.

例4 設(shè)f(x)=lnx-ax2+(2-a)x,

(1)討論f(x)的單調(diào)性.

(2)若函數(shù)y=f(x)的圖象與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明f′(x0)<0.

解析(1)當(dāng)a≤0時,f(x)在(0,+)單調(diào)遞增;

兩式相減得

lnx1-lnx2=a(x1+x2)(x1-x2)-(2-a)x1+(2-a)x2,

故f′(x0)<0.