時紅廷 李慧敏 陳江濤 高 暢

(首都師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,北京 100048)

1 引言和術(shù)語

分岔理論研究系統(tǒng)由于參數(shù)變化而引起的穩(wěn)定性變化過程,它分為靜態(tài)分岔和動態(tài)分岔兩個方面.本文所研究的內(nèi)容屬于靜態(tài)分岔理論.靜態(tài)分岔理論研究方程多個解相遇時的奇點情況.用來研究靜態(tài)分岔和動態(tài)的Hopf分岔問題的奇點理論和群論方法最初是在1970年前后由Thom R提出,隨后由Mather J給出了嚴(yán)格的數(shù)學(xué)證明.此后,Arnold V I([1],[2])以及Golubitsky([3～7])等人的工作大大豐富和發(fā)展了該方面的理論和應(yīng)用,本課題組的部分相關(guān)工作參見文獻(xiàn)[9～15].

設(shè)f∶U→R和g∶V→R分別是在原點(0,0)∈R2的鄰域U和V上有定義的C∞函數(shù).若存在(0,0)∈R2的鄰域W?U∩V,使得f|W=g|W,則稱f和g等價.顯然,這在由(0,0)∈R2的鄰域到R中的映射組成的集合中是一個等價關(guān)系,稱此等價關(guān)系的每個等價類為一個芽.所有這些芽構(gòu)成芽空間εx,λ,同理可定義芽空間ελ.

定義 1[7]設(shè)g∈εx,λ,稱(x0,λ0)是g(x,λ)的奇點,如果g(x0,λ0)=0,且g′x(x0,λ0)=0.

定義 2[7]設(shè)g∈εx,λ,稱(x0,λ0)是g(x,λ)的分岔點,如果g(x0,λ0)=0,且當(dāng)參數(shù)λ由小于λ0變?yōu)榇笥讦?的過程中,n(λ)發(fā)生了變化,其中n(λ)表示g(x,λ)=0的解的個數(shù).此時,我們也稱g(x,λ)=0是以x為狀態(tài)變量,λ為分岔參數(shù)的分岔問題.

靜態(tài)分岔理論用于研究形如h(x,λ)=0的分岔問題,這里h∈εx,λ.對它引進(jìn)等價關(guān)系,使之保持分岔情況不變.

定義 3[7]設(shè)g,h∈εx,λ,稱g與h等價,如果g(x,λ)=S(x,λ)h(X(x,λ),A(λ)),其中S,X∈εx,λ,A∈ελ,且S(0,0)＞0,X′x(0,0)＞0,X(0,0)=0,A(0)=0,A′(0)＞0.

特別地,若A(λ)≡λ,則稱g與h強等價.

定義 4[7]1)εx,λ中的線性子空間F稱為εx,λ中的理想,如果對任意的f∈F和a∈εx,λ,總有af∈F.

2)εx,λ中理想F稱為內(nèi)蘊理想,如果對g,f∈εx,λ,當(dāng)f∈F且g與f強等價時,g∈F.

定義 5[7]設(shè)g(x,λ)∈εx,λ,g(x,λ)的限制切空間是指εx,λ中有限生成理想RT(g)=[g,xgx,λgx].

對于εx,λ中線性子空間V,用codimV表示V在εx,λ中的余維數(shù).全文中μ=＜x,λ＞也即μ=

命題 1.1[7]設(shè)F是εx,λ中的真理想.那么,codimF＜+∞當(dāng)且僅當(dāng)存在正整數(shù)k使得μk?F.

命題 1.2[7]設(shè)F是εx,λ中的內(nèi)蘊理想,且codimF＜+∞,那么,F可表為下述形式：

其中m,mi,ri(i=1,2,3,…,n)皆為非負(fù)整數(shù).

文獻(xiàn)[7]指出,若F是εx,λ中的真內(nèi)蘊理想,則可選取命題1.1中的非負(fù)整數(shù)m,mi,ri(i=1,2,3,…,n)使?jié)M足

并將單項式xm,xm1λr1,xm2λr2,…,xmnλrn定義為F的內(nèi)蘊生成元.

但是,至今為止,對任意給定的εx,λ中的真內(nèi)蘊理想F,國內(nèi)外相關(guān)學(xué)者并沒有給出上述非負(fù)整數(shù)列的存在唯一性證明.

本文將證明,對任意給定的εx,λ中的真內(nèi)蘊理想F,存在唯一的一組形如(1.2)的非負(fù)整數(shù)列m,mi,ri(i=1,2,3,…,n)使得(1.1)式成立.此結(jié)論的重要性在于：我們首次證明了,對任意給定的εx,λ中的真內(nèi)蘊理想F,其內(nèi)蘊生成元組是唯一的.

內(nèi)蘊理想是應(yīng)用奇點理論研究靜態(tài)分岔問題的重要工具,且內(nèi)蘊生成元是解決分岔問題的識別問題的關(guān)鍵性概念.因此,對任意給定的εx,λ中的真內(nèi)蘊理想F,其內(nèi)蘊生成元組必須是唯一的,否則,內(nèi)蘊生成元的概念將無從談起.所以,本文的結(jié)果彌補了文獻(xiàn)[1]中的一點漏洞,是有意義的工作.

設(shè)F是εx,λ中理想,且codimF＜+∞,則易知：F是εx,λ中真理想當(dāng)且僅當(dāng)F≠εx,λ.

因此,本文只需對真理想進(jìn)行研究即可.

2 預(yù)備性命題

在給出主要結(jié)論之前,首先給出若干命題.

命題 2.1設(shè)F是εx,λ中真理想,且codimF＜+∞.那么,F是內(nèi)蘊理想當(dāng)且僅當(dāng)F可表為下述形式之一：

(1)存在正整數(shù)k,使得F=μk;

(2)存在正整數(shù)k,s和非負(fù)整數(shù)ki,li(i=1,2,3,…,s),使得

證明：命題1.1和命題1.2的直接推論.

命題2.2設(shè)F是εx,λ中真內(nèi)蘊理想,codimF＜+∞,且對任意正整數(shù)m,F≠μm.那么,存在正整數(shù)k,s和非負(fù)整數(shù)ki,li(i=1,2,3,…,s),使得

其中k＞k1+l1＞k2+l2＞……＞ks+ls＞0,且0＜l1＜l2＜……＜ls.

證明：因為F是εx,λ中真內(nèi)蘊理想,codimF＜+∞,且對任意正整數(shù)m,F≠μm,于是由命題1.2知,存在非負(fù)整數(shù)k,s,ki,li(i=1,2,…,s),使得(2.1)式真.

因為F是εx,λ中真理想,所以k是正整數(shù)(若不然,則k=0,于是μk=μ0=εx,λ,于是F=εx,λ,這與F是εx,λ中真理想相矛盾.)

若某個li=0,則μki＜λli＞=μki,從而μk+μki＜λli＞=μk+μki=μmin{k,ki};又因?qū)θ我庹麛?shù)m,F≠μm,故li不全為零.所以,不妨設(shè)li(i=1,2,…,s)皆為正整數(shù).

若對某個ki+li,有ki+li≥k,則μki＜λli＞?μk,從而μk+μki＜λli＞=μk,于是μki＜λli＞可從表達(dá)式中去掉.所以,不妨設(shè)k＞ki+li(i=1,2,…,s).

若對某i,j,有l(wèi)i=lj,則μki＜λli＞+μkj＜λlj＞=μmin{ki,kj}＜λli＞.所以,不妨設(shè)i≠j時,li≠lj.所以,不妨假設(shè)0＜l1＜l2＜……＜ls.

若對某個i,ki+li≤ki+1+li+1,其中1≤i＜s.因li＜li+1,于是,μki+1＜λli+1＞中所有生成元皆在μki＜λli＞中,從而μki+1＜λli+1＞+μki＜λli＞=μki＜λli＞,于是μki+1＜λli+1＞可從表達(dá)式中去掉.于是,不妨假設(shè)ki+li＞ki+1+li+1(i=1,2,…,s-1).

綜上知,命題2.2得證.

3 主要結(jié)論和證明

下述定理是命題1.2的推廣.

定理 3.1設(shè)F是εx,λ中真理想,且codimF＜+∞.那么,F是內(nèi)蘊理想當(dāng)且僅當(dāng)F可表為下述形式之一：

(1)存在唯一的正整數(shù)k,使得F=μk;

(2)存在唯一的一組正整數(shù)k,s和非負(fù)整數(shù)ki,li(i=1,2,3,…,s),使得

其中k＞k1+l1＞k2+l2＞……＞ks+ls＞0,且0＜l1＜l2＜……＜ls.

證明：?)(充分性)顯然真.

?)(必要性)設(shè)F是εx,λ中真內(nèi)蘊理想,且codimF＜+∞.

因codimF＜+∞,于是由命題1.1知,存在唯一的正整數(shù)k使得μk?F,且μk-1?F.

若F=μk,則必要性得證.不妨設(shè)對任意正整數(shù)m,F≠μm.于是由命題2.2知,存在正整數(shù)k,s和非負(fù)整數(shù)ki,li(i=1,2,3,…,s),使得(3.1)式真,其中k＞k1+l1＞k2+l2＞……＞ks+ls＞0,且

下面將證明：F滿足(3.2)的形如(3.1)的表達(dá)式是唯一的.

欲證F滿足(3.2)的形如(3.1)的表達(dá)式是唯一的,即要證

斷言1：k=

事實上,若斷言1不真,則k≠不妨設(shè)k＜則xk∈μk?F,也即有

于是可設(shè)

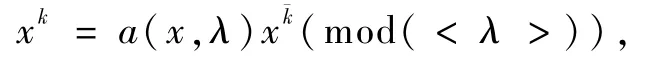
其中a(x,λ)∈εx,λ.

斷言2：

也即

可設(shè)

斷言3：

事實上,若斷言3不真,則由斷言2,不妨設(shè)ks由于

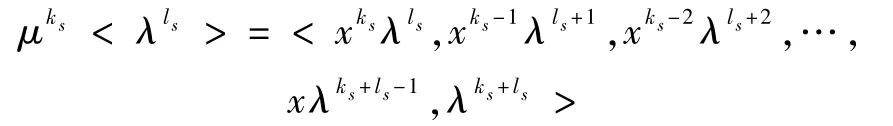
且

所以

可設(shè)

其中ai(x,λ)∈εx,λ(i=0,1,…,k),aji(x,λ)∈εx,λ(j=1,2,…,s;i=0,1,…,kj).因

斷言4：

可設(shè)

其中ai(x,λ)∈εx,λ(i=0,1,…,k),aji(x,λ)∈εx,λ(j=1,2,…,s;i=0,1,…,kj).因

斷言5：

事實上,若斷言5不真,則由斷言4,不妨設(shè)ks-1＜,且ls-1＞.由于

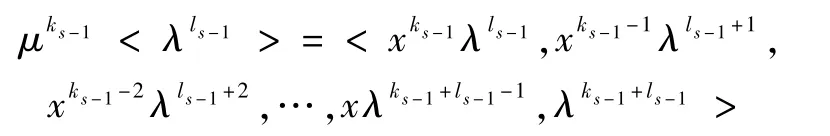
且

所以

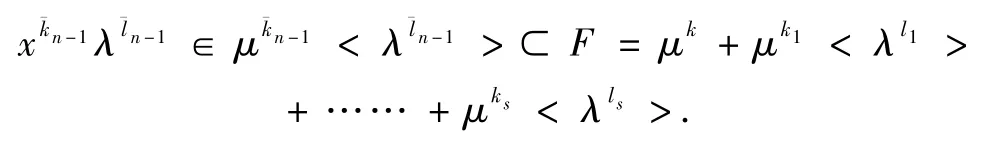
可設(shè)

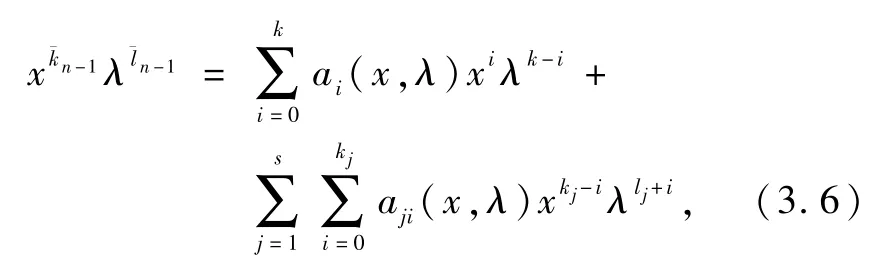
其中ai(x,λ)∈εx,λ(i=0,1,…,k),aji(x,λ)∈εx,λ(j=1,2,…,s;i=0,1,…,kj).因

依此類推,我們證知：

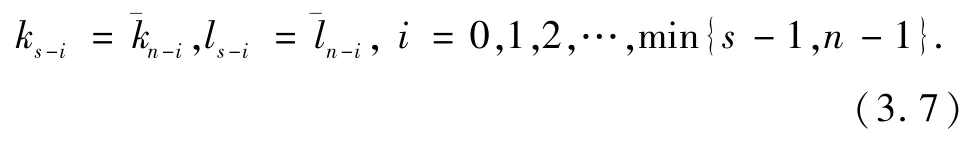
斷言5得證.

斷言6：s=n.

事實上,若斷言6不真,不妨設(shè)n＜s.由斷言1和(3.7)知,

可設(shè)

其中

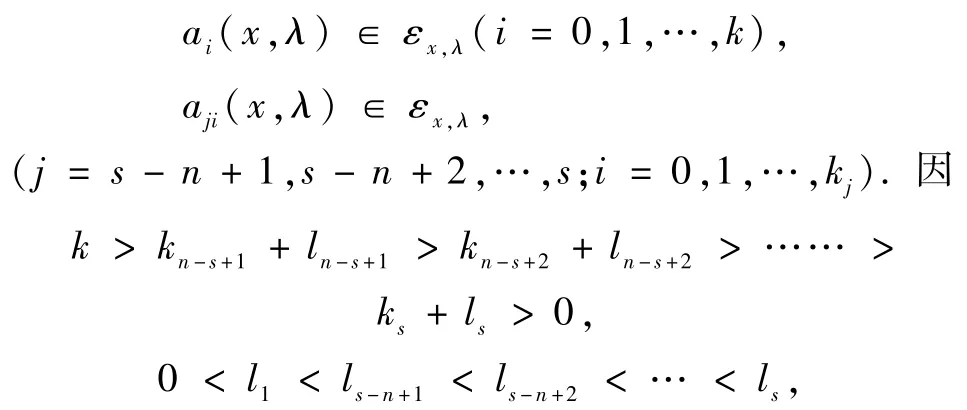
綜合斷言1～6知,定理3.1得證.