Haijiao WANG , Zhen YANG ,*, Wugen ZHOU , Dalin LI

a University of Chinese Academy of Sciences, Chinese Academy of Sciences, Beijing 100190, China

b National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China

KEYWORDS Deep reinforcement learning;Dynamic scheduling;Image satellites;Neural network;Online scheduling

Abstract In the ‘‘Internet Plus” era, space-based information services require effective and fast image satellite scheduling. Most existing studies consider image satellite scheduling to be an optimization problem to solve with searching algorithms in a batch-wise manner. No real-time speed method for satellite scheduling exists. In this paper, with the idea of building a real-time speed method, satellite scheduling is remodeled based on a Dynamic and Stochastic Knapsack Problem(DSKP), and the objective is to maximize the total expected prof it. No existing algorithm could be able to solve this novel scheduling problem properly. With inspiration from the recent achievements in Deep Reinforcement Learning(DRL)in video games,AlphaGo and dynamic controlling,a novel DRL-based method is applied to training a neural network to schedule tasks.The numerical results show that the method proposed in this paper can achieve relatively good performance with real-time speed and immediate respond style.

1. Introduction

During the‘‘Internet Plus”era,real-time information service is one of the important functions of space-based internet information systems.1Effective and fast image satellite scheduling is the key to maintaining stability and providing space-based information services.2However, image satellite scheduling is notoriously difficult as an NP-hard problem. Furthermore,real-time information services require real-time scheduling,which requires both immediate responses and real-time running performance.

Over past few decades,scholars in related fields have shown interest in this problem: Potter et al.3studied the scheduling problem of a linear finite deterministic model using a backtracking method. By focusing on the arrival of new tasks,Liu and Tan4modeled the problem of multi-satellite dynamic scheduling based on Dynamic Constraints Satisfaction Problem (DCSP) and proposed a search algorithm to solve the model. Lema??tre et al.5,6studied the management of satellite resources and the observation scheduling of agile satellites.They further compared the performance of a greedy algorithm,a dynamic programming algorithm,and a constraint programming algorithm. Li et al.7proposed a fuzzy neural network to choose the timing of dynamic scheduling and then implemented a hybrid rescheduling policy. Liu8proposed three descriptive models and turned the dynamic scheduling problem into a random and fuzzy scheduling problem. In recent years, the particle swarm optimization,9the genetic algorithm10-12and other heuristic search algorithms13-16were applied to this domain. In addition, many other scholars have studied the problem of satellite management from different perspectives: Some scholars try to only reschedule the disturbed area restoratively to improve the response speed17and others try to solve the dynamic scheduling problem when an initial scheduling scheme is absent, such as a multi-agent system18-20and rolling scheduling.21

Generally, most of the existing studies schedule tasks in a batch-wise manner; these studies consider image satellite scheduling as an optimization problem, and intelligent optimization algorithms or heuristic algorithms are applied to solving these optimization problems; both of algorithms require time to collect information of tasks, and schedule collected tasks in a batch-wise manner (in a batch-wise manner,one collects tasks first, then schedules them once, and the scheduling usually happens at the end of scheduling period).

A few researches could respond tasks with immediate style based on some heuristic rules or expert knowledge. However,these rules are usually hard to obtain and have a limited range of applications.2

Deep Reinforcement Learning (DRL) is about learning how to maximize a numerical reward signal.22Reinforcement learning is an ideal solution for dynamic decision-making problems. At present, a series of deep reinforcement learning algorithms, such as DQN (Deep Q-Learning Network),23DPG (Deterministic Policy Gradient),24and DDPG (Deep Deterministic Policy Gradient),25are proposed. These algorithms have a wide range of applications, such as Go26,27and resource allocation.28

In this paper, a novel DRL-based method is proposed to build an image satellite scheduling solution with immediate response capability and real-time speed:First,we build a novel satellite scheduling model based on the Dynamic and Stochastic Knapsack Problem (DSKP); the objective of this novel model is to maximize the total expected prof it instead of the total current prof it, which allows us to schedule tasks without f inishing collecting all the tasks, and to respond to a task immediately whenever it arrives. Second, we build a network(which is known as the scheduling network in the rest of this paper) and train this network to learn how to schedule with Asynchronous Advantage Actor-Critic (A3C) algorithm, a DRL algorithm. If well-trained, the scheduling network could schedule tasks in an immediate response style without further training. In addition, because reinforcement learning is an online learning method, scheduling network could keep improving its performance or adapt to the change in environment through continuous training.

The rest of this paper is organized as follows. The description and mathematical statements of our model are discussed in Section 2.In Section 3,the architecture and training method of the scheduling network are shown. In Section 4, a series of simulations are run to test and analyze the proposed method.

2. Problem description and mathematic statement

2.1. Classic model about satellite dynamic scheduling

In classic studies, the dynamic scheduling of image satellite is described as follows: given a finite time period and an image satellite with limited storage,tasks arrive dynamically,the time windows of the satellite for tasks can be obtained through preprocessing, and the tasks could only be observed inside the time windows. If task is accepted successfully, the prof it associated with the accepted task is received. The objective is to maximize the total prof it from accepted tasks at the end of given time period.

As we mentioned in Section 1, the model of image satellite dynamic scheduling is usually built as an optimization problem, which has the similar formation as follows:

subject to

where G is the total prof it, ωiis the prof it of the i th task, and Diusually indicates the decision for the i th task.Eq.(2)represents the constraints of the satellite, which are usually related to resources such as storage, and time constrains. Satellite could only observe one task at a time.

Apparently, models like Eq. (1) require all tasks involved throughout the time period.Because the full tasks’information could only be obtained at the end, an effective and immediate scheduling response would not be very difficult.

2.2. Satellite scheduling model based on DSKP

Kleywegt and Papastavrou29studied a Dynamic and Stochastic Knapsack Problem (DSKP), and the DSKP is knapsack problem in dynamic and changing environment.In the DSKP,a pack of limited size is given, items with different values and sizes arrive dynamically,and an immediate decision(accept or reject)for each item must be made immediately.The goal is to obtain more total value without breaking limit of the pack’s size.

Based on DKSP and classic model of satellite scheduling,we remodeled the image satellite dynamic scheduling problem.The image satellite scheduling problem with immediate response requirement is described as follows: Given an image satellite with limited storage, tasks arrive dynamically. Each task has an associated prof it. The prof it of a task is unknown prior to arrival and becomes known upon arrival. Each arriving task can be either accepted or rejected.If a task is accepted,the prof it associated with the task is received.This process will stop when the deadline is met or the satellite is exhausted(when it has no remaining storage or no enough free time to accept a task, just like a full pack). The objective is to maximize the total prof it of the accepted tasks when stopped.However, the decision for each task should be made right after its arrival. The satellite could accept a task if and only if the remaining storage is suff icient and the task has no time conf lict with previous accepted tasks (see Fig. 1). And we make an assumption that a task cannot be recalled once it is rejected,i.e., once the decision of a task is made, it cannot be changed.

Let the StorMaxbe the storage limit of a satellite, and let Stor t（ ） denote the remaining storage of satellite on time t; let tfreet（ ）denote the free time intervals for accepting tasks on time t, and let ttransbe the shortest transfer time between tasks.tfreet（ ） is defined as follows:

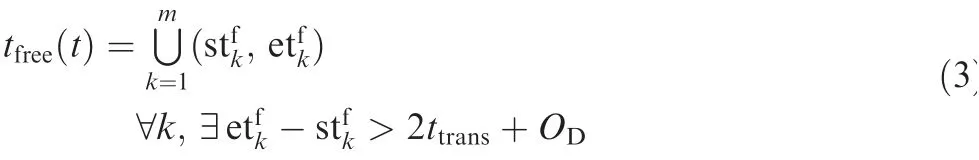
When a task arrives in the system, a decision about its acceptance is made based on the scheduling policy.A scheduling policy is a strategy or criterion that could determine a task’s acceptance based on the state of the system. The state of the system includes the state of the arriving task, and the resource state of the satellite.

Let π be the policy used to make scheduling decisions.is the decision made for the i th task under policy π, andis defined as follows:

The expected total prof it at time t=Aiunder the policy π could be defined as follows:

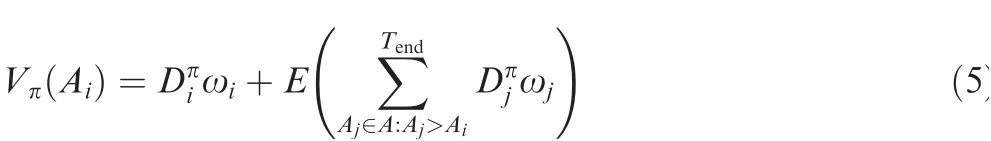
where Tend=min（T, Tstor, Tfree）, Tstoris the time when the storage is exhausted(Stor Tstor（ ）≤0)and Tfreeis the time when no free time is available to accept task (tfreeTfree（ ）=?).is made at Ai. ωjand Ajdenote the prof it and the arrival time of the j th task respectively; the j th task is the task that arrives after the i th task. Typically, Vπ0（ ） denotes all the expected total prof it that could be obtained under policy π throughout the whole time period.

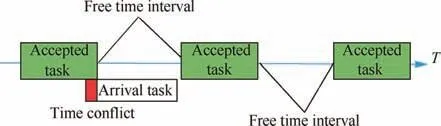
Fig. 1 Time conf lict and free time of satellite.

Let ∏πdenote all the policies that we could use.The objective is to f ind the optimal total expected prof it

Apparently,the optimality of Vπdepends on the optimality of π, and thus we must f ind an optimal π*.

The current scheduling algorithms are designed to build an optimal scheduling solution with search algorithm under given tasks and satellite. They could be regarded as a scheduling policy which needs full information of all tasks;therefore, they could not adapt to a model with uncertainties.

Inspired by AlphaGo27and AlphaGo Zero,30which uses neural network as function approximator and pattern matcher to evaluate the game Go and choose the next move (i.e., an policy of Go), we parameterized the scheduling policy with neural network, and we expect to f ind the optimal scheduling policy with reinforcement learning method.

A summary of the most important notation is given in Table 1.

3. DRL-based method for dynamic scheduling

3.1. Introduction of DRL

DRL is the process of learning what to do—how to make optimal decisions—in a dynamic environment.22More importantly, reinforcement learning has very wide range of uses in sequential-decision making problems, such as αGo27,30and robot control.31In these problems,a series of decisions should be made to achieve an optimal cumulative reward (or longterm benef it), such as winning a game of αGo or maintaining balance as long as possible.

The basic idea of reinforcement learning is shown in Fig.2,the agent makes decisions Diusing the observed state siof the environment; Then a new state and an immediate reward Risignal is received. The goal is to obtain more cumulativerewards.To get the optimal cumulative reward,reinforcement learning usually has a similar iterative formula as follows22:

Table 1 Summary of notations.

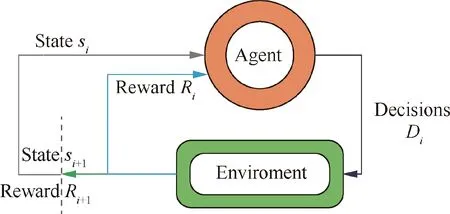
Fig. 2 A simple illustration of reinforcement learning.

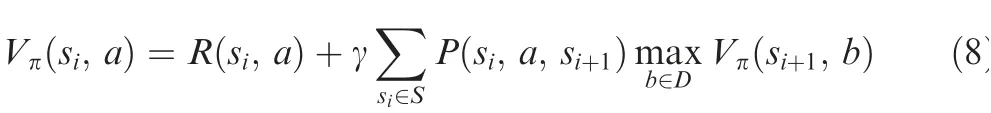
where siis the current state, si+1is the next state, and S is all the possible states; a and b are the decisions for siand si+1respectively; D is all possible and logical decisions; Riis the immediate reward, and Vπis the cumulative reward (longterm benef it).γ is the discount factor used to control the future influence, and it should be less than 1 if the time is infinite.P（si,a,si+1） is the transition rate between state siand si+1with decision a.In the model-free reinforcement learning algorithm,P（si, a, si+1） does not need to be known as prior knowledge.

From Eq. (8), we can see that the DRL algorithm learns how to predict long-term benef it with current state based on an iterative and bootstrap procedure. With enough training,the DRL algorithm would learn to predict the future longterm benef it based on current state as well as try to make decision with higher future long-term benef it based on current state.22

3.2. Scheduling network

Eq.(5)and Eq.(8)have similar forms,they all indicate how to get more expected future prof it, and it is clear that DRL is an ideal solution for our model. So, we adopt one of the DRL algorithms to learn the scheduling policy.

3.2.1. Architecture

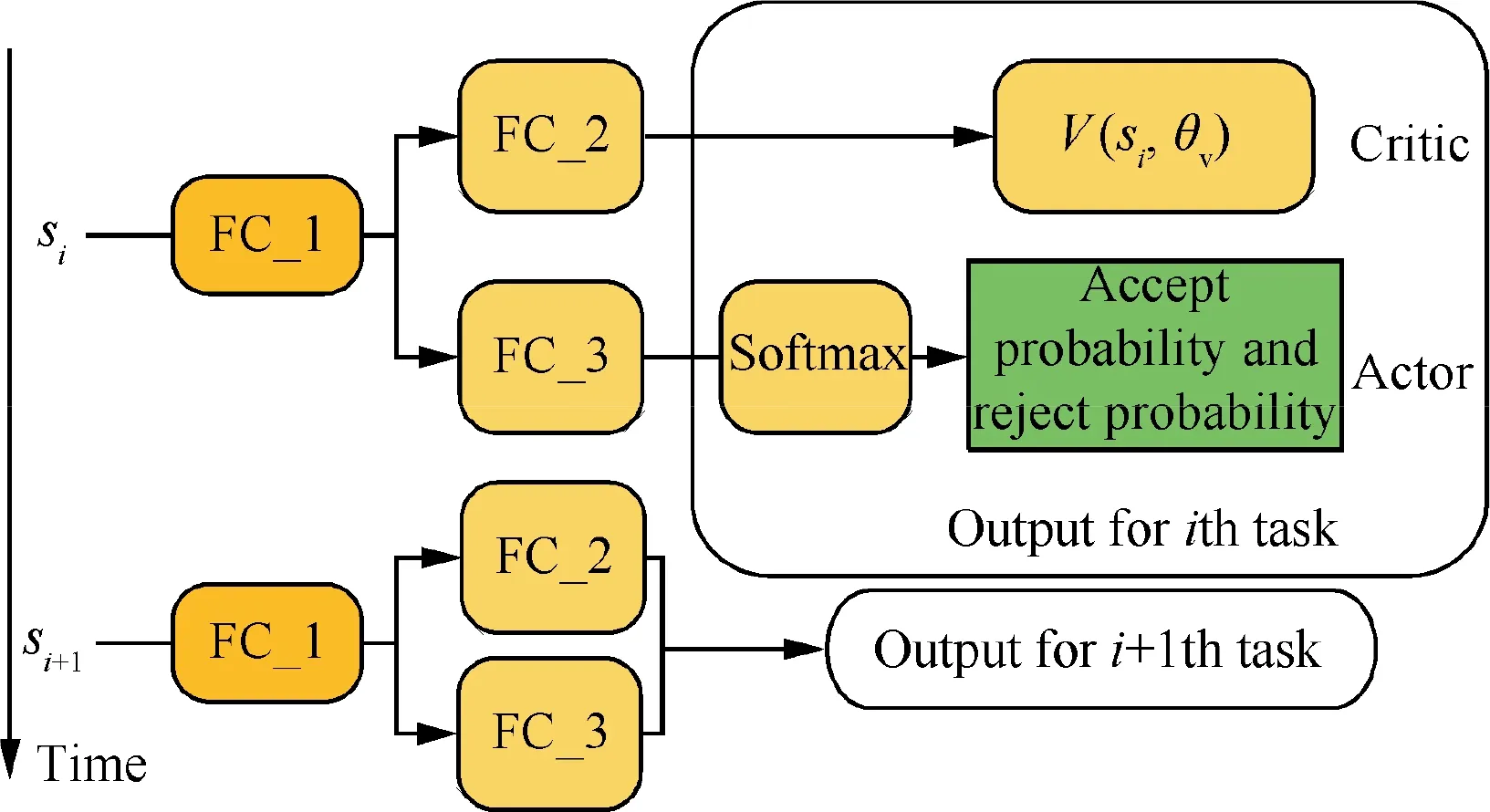
Fig. 3 Architecture of scheduling network.

The output of the network has two parts: an estimation value of total expected prof it (denoted as V（si; θv）) as Critic and the decision (denoted as（si, θπ）) for task as Actor(see Fig. 3). θvis the network parameters of the Critic, and θπis the network parameters of the Actor.

If a task is accepted, the time window inside the longest free time interval is chosen as the observation time for the task.

The network consists of three fully connected layer, each layer is followed with Relu activation function ().

The parameters of the network are shown in Table 2.

3.2.2. Training method

We adopted the Asynchronous Advantage Actor-Critic(A3C)32to implement and train our scheduling network because of its stability and high usability. As a model-free DRL algorithm, A3C allows us to train the scheduling network without knowing the task distribution as prior information.

A train program based on Satellite Tool Kit (STK) is designed to simulate dynamic scheduling situation, include tasks,and provide time windows for these tasks.During training, the training program continues to produce new task for scheduling work to schedule until Tend(see Fig.4):when a task arrives,the scheduling network makes a decision about it,and then receives an instant reward.The instant reward is not used to train the network directly because this instant reward could not represent the following influence of the decision. During training, the parameters of networks are updated after every N-Steps. And the advantage value (see Eq. (11)) of each decision is used to train the scheduling network,and the advantage value (see Eq. (11)) is numerical reward value with respect to the future rewards.

The Actor could learn to make optimal decisions Dπi for task, while the Critic learn to predict expected total prof it Vπ.The Critic improves its prediction ability based on the real cumulative prof it at the end of each situation. And the Actor improves its scheduling ability based on the prediction from Critic.Scheduling one task is referred to as a step.The parameters of networks are updated after every N-Steps (denoted as T-Stepmaxor reaching the Tendof a scheduling episode (see Fig. 4).

The parameters of the networks are updated by the algorithm that could be defined as follows32:

Table 2 Conf iguration of networks.

Fig. 4 N-Steps training process.

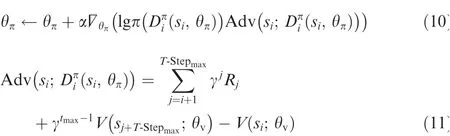
where α is updating rate of network’s parameters. ?θπis the gradient operator.

The reward for the decision is the prof it of the task,which is defined as follows:

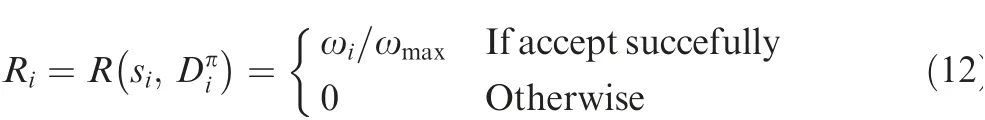
where ωmaxis the maximum prof it of a task.

4. Presentation of results

Numerical simulations are run to fully test and analyze the performance of the scheduling network. The scheduling networks are implemented in Python language,and deep learning framework of TensorFlow33is utilized. Because there is no benchmark dataset for image satellite scheduling, we designed a program to generate tasks during these simulations.Besides,STK is used to simulate the satellite and calculate the time windows of the tasks.

4.1. Performance analysis

4.1.1. Training

To support our idea of introducing deep reinforcement learning into image satellite scheduling, we trained scheduling network and conducted some simulations. Parameters of satellite and tasks in these simulations are given in Table 3.

Table 3 Parameters of satellite and tasks during training.

Table 4 Hyper-parameters of training.

The hyper-parameters used in training process are referred to Ref.32, and values of these hyper-parameters are shown in Table 4.

First, we train our network to schedule tasks for different time periods (see Fig. 5). The total prof it, total accepted task count, and average prof it (the ratio with respect to the total prof it and total accepted task count) are selected as indexes to evaluate the training performance. The results are shown in Fig. 5. Because each episode consists of different tasks, we the average value to show the clear changing trend of performance (the red lines in Fig. 5).

The scheduling network could achieve a higher total prof it in every simulation through training, which indicates that the proposed method works.

During scheduling, two factors affect the total prof it,namely accepting more tasks (usually meaning solving time conf licts between tasks) and choosing tasks with higher prof it(usually leading to a higher average prof it). In Fig. 5, we noticed that the scheduling part of the simulations learned to obtain higher average prof its and accepted more tasks.

From Fig. 5, we can see that the network could learn to adapt to them and learn to how to schedule,which largely indicates that the scheduling network could f ind a stable scheduling policy π*that could produce satisfying solution real-time speed and immediate respond style.

4.1.2. Generalization and test

In this simulation, we try to test well-trained scheduling network. First, we train our scheduling network with the setup of Fig. 6(a); we then continue to apply the well-trained scheduling network in other simulations (see Figs. 6(b) and 6(c)) without further training.

The parameters of these simulations are shown in Table 5.The results are shown in Fig. 6.

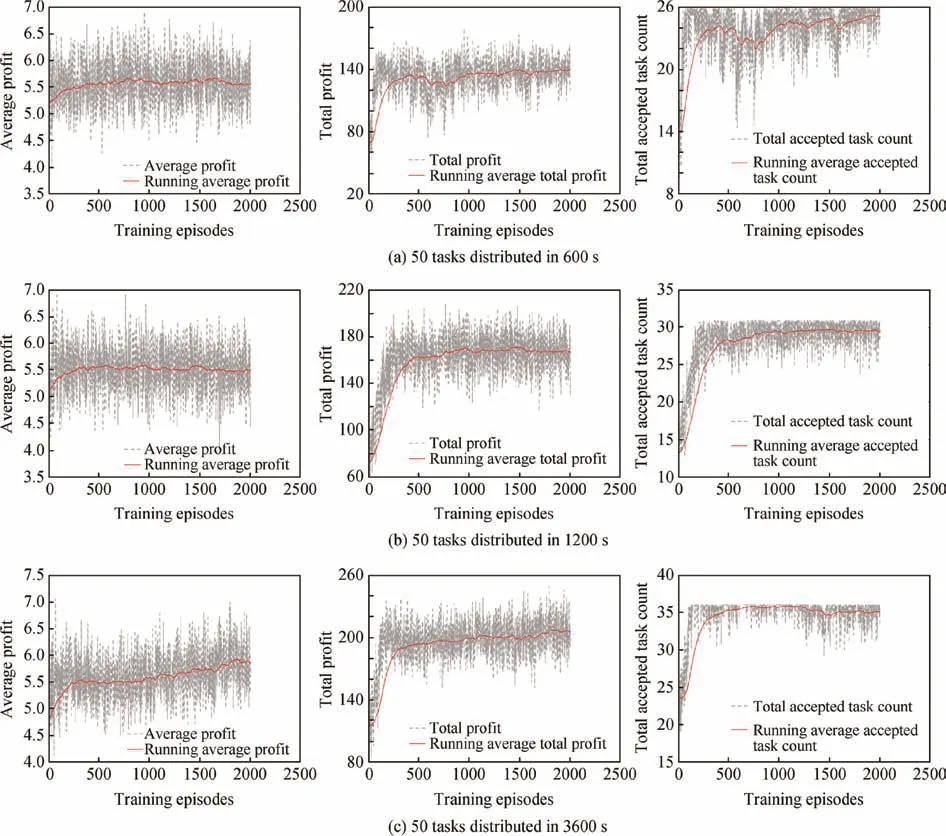
Fig. 5 Training curves of performance.

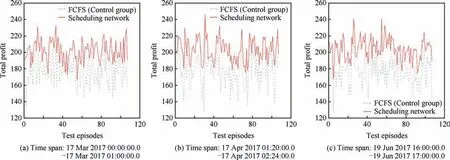
Fig. 6 Generality test of scheduling network.

Compared to the First Come First Serve (FCFS) (Control group), the scheduling network could show a stable performance in both testing simulations (see Fig. 6(b) and 6(c)) and training simulations (see Fig. 6(a)), which shows the stability and generalization ability of the scheduling network.

4.1.3. Adaptability

In this section, we trained our scheduling network for 10000 episodes. Within the first 3000 episodes, each episode consistsof 45-55 tasks;then we change the arriving task count of each episode to 95-105.In this way,we expect to validate the adaptability of the scheduling network. The simulation parameters are the same as those of Fig. 5(c) besides the task count. The results are shown in Fig. 7.

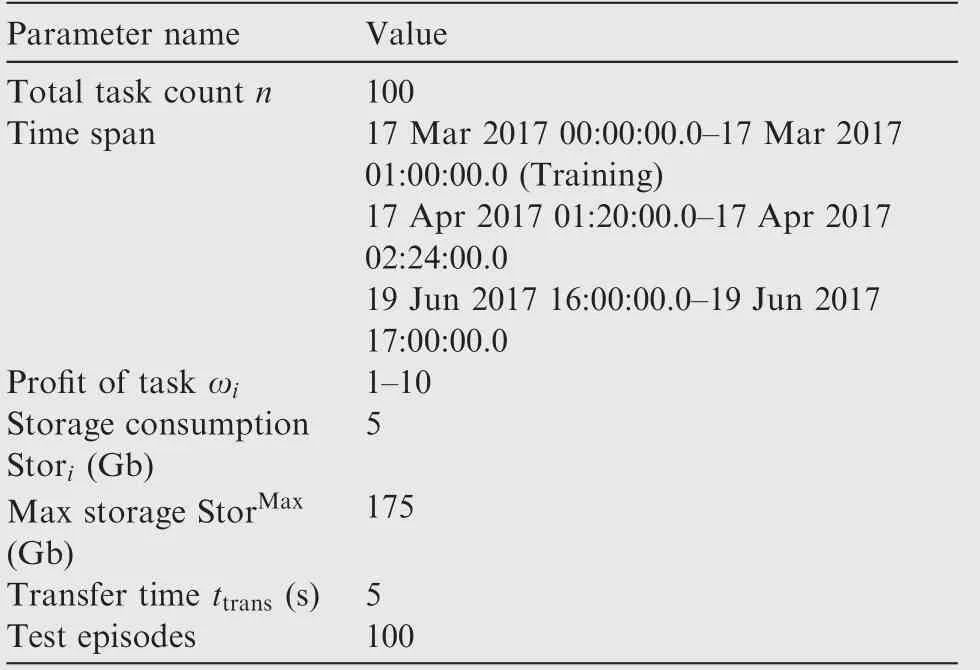
Table 5 Parameters of satellites and tasks.

As shown in Fig. 7, although the total count of accepted tasks stays the same due to the limitation in resources(the storage has been almost exhausted with 35 accepted tasks)after we increase the total count of tasks, the total prof it continues to grow.This result occurs because,with the total count of arriving task growing to 95-105,the scheduling network changes its decision policy through training; scheduling network learns to accept tasks with higher prof it.As evidence,the average prof it grows after we increase the total task count. This result indicates that the scheduling network could adapt to a new environment once the environment is changed.

Thus, we could draw a conclusion that the scheduling network could be applied to scheduling tasks without further training once it is well-trained (see Section 4.1.2). In addition,scheduling network could adapt to the change in the environment (see Section 4.1.3).

4.2. Comparison with other algorithms

To fully test and analyze the proposed method,we run a series of simulations to compare our method with other algorithms,including FCFS,21Direct Dynamic Insert Task Heuristic34(Dynamic Insert Task Heuristic is referred to as DITH in this paper)and Genetic Algorithm(GA).11A random pick method(this method randomly accepts or rejects tasks) is used as the control group.

We generate 20 different series of tasks to compare our scheduling network with the classic algorithms. The average total prof it, the average accept task count, the average prof it of tasks, and the average response time for tasks are taken as index. The simulation results are shown in Table 6.

Compared with the FCFS, scheduling network could achieve better performance. And compared with intelligent optimization algorithms (GA and DITH), scheduling network shows improvement in response time.

More importantly,scheduling network could schedule tasks in an immediate style while other algorithms like GA and DITH need to collect tasks, and then schedule them once in a batch-wise manner. However, collecting tasks takes time,for example, due to the different arrival time, the first task has to wait for the last task in batch-wise manner,which makes the first task get a very slow response.

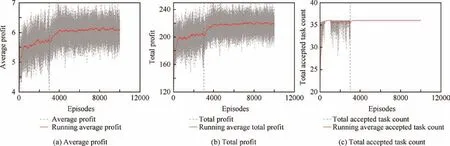
Fig. 7 Adaptability test.

Table 6 Performance comparison (Total Task Count=50, T=3600 s).

5. Conclusions

Image satellite scheduling is very important for providing effective and fast space-based information services.A novel satellite scheduling model based on the DSKP was proposed.Unlike the classical satellite scheduling model,the objective of this mode is to maximize the total expected prof it rather than total prof it,which allows us to schedule tasks in an immediate style. Due to the complexity of the problem, it is very difficult to obtain an optimal solution or heuristic rules.Therefore,the scheduling network based on DRL was proposed. Scheduling network could be trained to schedule tasks in an immediate response style, and no special expert knowledge was needed. If welltrained,the scheduling network could schedule tasks effectively and quickly.Our main contribution was proposing a real-time scheduling method for image satellite by importing DRL and neural networks into satellite scheduling.

In future work, we plan to import imitation learning into the proposed method to improve learning stability and performance, and we plan to extend our method to multi-satellite scheduling situations.

Acknowledgements

This study was co-supported by the Key Programs of the Chinese Academy of Sciences (No. ZDRW-KT-2016-2) and the National High-tech Research and Development Program of China (No. 2015AA7013040).