Third-Order Magnetic Susceptibility of an Ideal Fermi Gas?
Long-Quan Lai(賴龍泉),Zhao Li(李照),Ya-Bin Yu(余亞斌),and Quan-Hui Liu(劉全慧)
School for Theoretical Physics,School of Physics and Electronics,Hunan University,Changsha 410082,China
AbstractAt low temperature and under weak magnetic field,non-interacting Fermi gases reveal both Pauli paramagnetism and Landau diamagnetism,and the magnitude of the diamagnetic susceptibility is 1/3 of that of the paramagnetic one.When the temperature is finite and the magnetic field is also finite,we demonstrate that the paramagnetism and diamagnetism start to deviate from the ratio 1/3.For understanding the magnetic properties of an ideal Fermi gas at quite low temperature and under quite weak magnetic field,we work out explicitly the third-order magnetic susceptibility in three cases,from intrinsic spin,orbital motion and in total.An interesting property is in third-order magnetic susceptibilities:when viewing individually,they are both diamagnetic,but in total it is paramagnetic.
Key words:Fermi gas,third-order magnetic susceptibility,Pauli paramagnetism,Landau diamagnetism
1 Introduction
The nature of the physical world is essentially nonlinear,and the linear approximation only applies locally or other certain exceptional circumstances.As is wellknown,[1?3]Pauli paramagnetism and Landau diamagnetism for an ideal Fermi gas under weak magnetic field and at low temperature give linear relation between the magnetization M and the external magnetic field H,i.e.,M= χ1H,where χ1is the magnetic susceptibility that depends on the temperature T and the intrinsic parameters of the system itself,such as number density n and magnetic momentμBof an electron,without referring to the external field.Explicitly,the susceptibilities for Pauli paramagnetism and Landau diamagnetism at low temperature are,respectively,
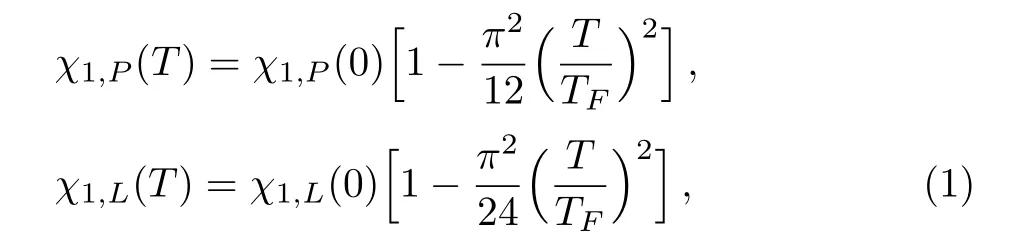
where the number 1 in the subscript denotes the first-order susceptibility,and TFis the Fermi temperature defined byvia Fermi energy εF,and
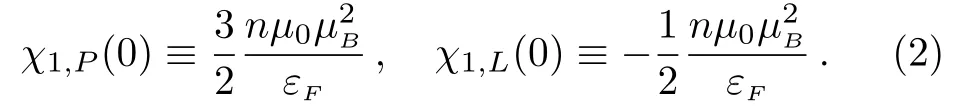
Here is a well-known 1/3-law that defined by the ratiowhere the magnitude of the diamagnetic susceptibility is one third of that of the paramagnetic one.
In a metallic free electron gas,with a typical Fermi temperature of 105K,the room temperature can be approximately treated as zero temperature for the ratio T/TF~ 10?3is too small.Thus the zero-temperature susceptibilities for Pauli paramagnetism and Landau diamagnetism offer value accurate enough for some practical purposes in history.With the development of laser cooling,however,ultracold atoms can be prepared with almost complete control over their density,temperature,interactions,effective magnetic field and the magnitude of the Fermi energy,etc.For instance,different laboratories report varying ranges of values of the ratio T/TFfrom 0.5 to 240,[4]0.13 to 0.33,[5]0.24 to 0.35,[6]and 0.03 to 0.06.[7?8]With fermionic ultracold atomic gases,the typical temperature ratio T/TF≈0.30 is two orders larger than the usual one for metallic free electron gas.It makes the temperature correction in Eq.(1)no longer negligible with T/TF≤1,as it was experimentally confirmed.[6]
What is more important,for neutral quantum gases in which the orbital motion has insignificant contribution,only the paramagnetism is practically accessible,and the higher order for Landau diamagnetism is of theoretical importance in understanding the origin of the relevant magnetism.Experiments[6]clearly indicate that once the effective magnetic field increases,the relation of the magnetization versus the magnetic field deviates from the linear one and becomes a sublinear and nonlinear one.In other words,third-order magnetic susceptibilities arising from the intrinsic spin must be diamagnetic,and it needs to be examined.
Let us now give the definition of the higher-order magnetic susceptibility at weak- field limit.Up to the third order,the magnetization can be written as an expansion of the external magnetic field
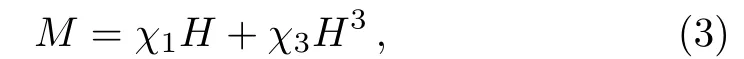
where χ3is the third-order magnetic susceptibility.The terms of H with even number power do not exist for the reverse of direction of the external field must accompany the turnover of direction of the magnetization.The resultant relation between H and magnetic induction B is
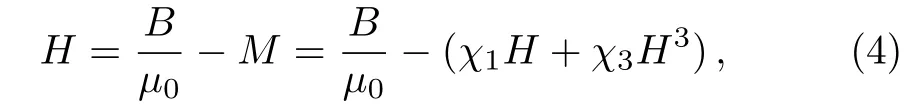
whereμ0denotes the permeability of free space.To note that when B is weak enough,we can expand H in powers of B.The relation between H and B then becomes
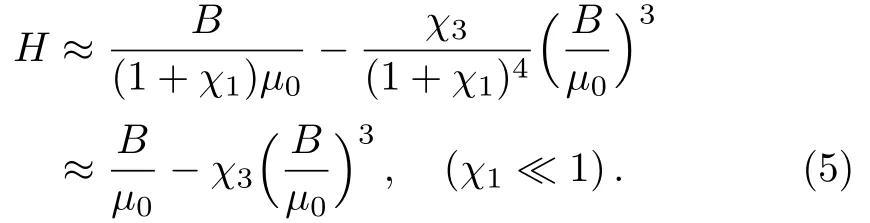
The dependence of the magnetization M on B is
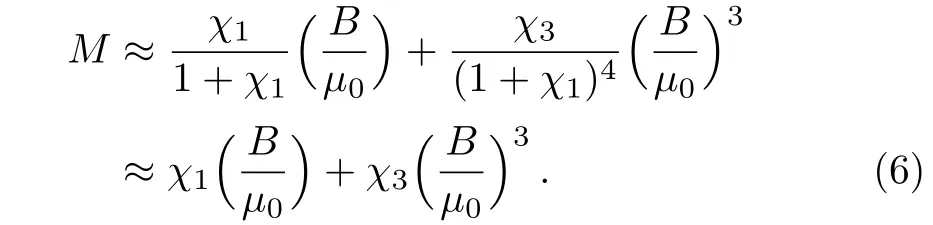
As a consequence,the expressions of χ1and χ3are,respectively,
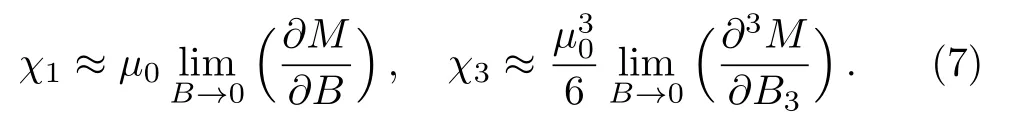
In principle,statistical mechanics offers the general formalism leading to an arbitrary order of the magnetic susceptibility.[1?3]However,the computational complications increase dramatically if one attempts the analytical results of higher-order susceptibility,and great care that must be taken when dealing with the higher-order expansions of various functions.Fortunately,the thirdorder magnetic susceptibility can be calculated straightforwardly.Such an exploration is important to understand,for instance,where the discrepancy of the 1/3-law originates from.
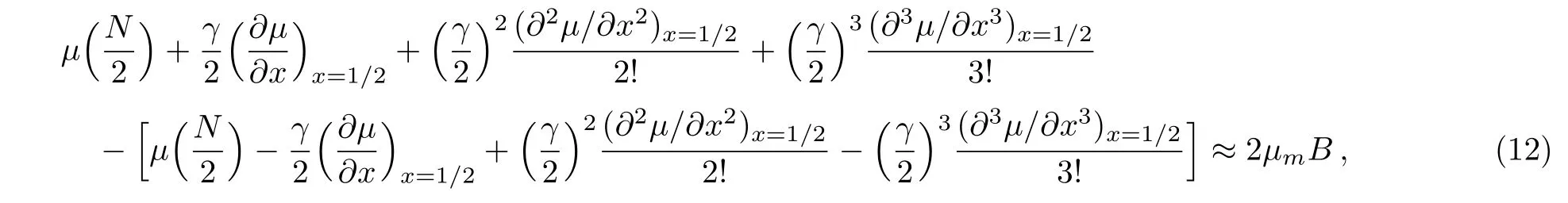
Paramagnetism and diamagnetism can be produced not only solely but also simultaneously in experiments.[6,9]In Secs.2 and 3,we calculate the third-order magnetic susceptibilities for Pauli paramagnetism and Landau diamagnetism systems,respectively.Since the mutual interplay of the intrinsic spin and orbital motion plays a crucial role in understanding the magnetic properties,in Sec.4 we study the total susceptibility under weak magnetic field.Section 5 presents discussions and conclusions.
In this paper,the external magnetic field B is put along the z-axis,and the magnitude of the field is constant.
2 The Third-Order Magnetic Susceptibility of the Pauli Paramagnetism System
The energy of a particle with magnetic momentμmin the presence of an external magnetic field B is given by
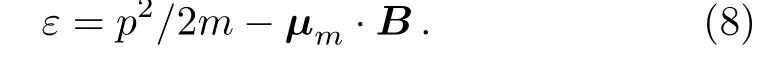
Assuming that the spin quantum number of the particle is 1/2,and the applied field B shifts the energies of the two spin states in opposite directions.With a given total number N of the particles,the number N+of spin-up component is determined by the following chemical potential difference[1?3]
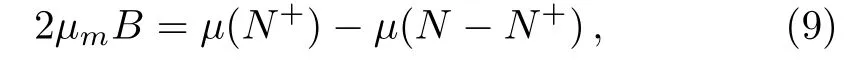
whereμ(N+)denotes the chemical potential for the spinup component,whereasμ(N?N+)for the spin-down one.
To obtain an explicit expression of the magnetic susceptibility,we introduce a dimensionless parameter γ with
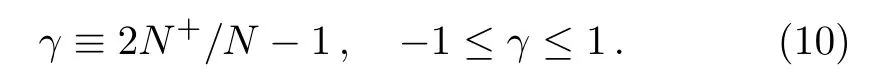
The foregoing Eq.(9)becomes with N+≡(1+γ)N/2 and N?≡(1?γ)N/2
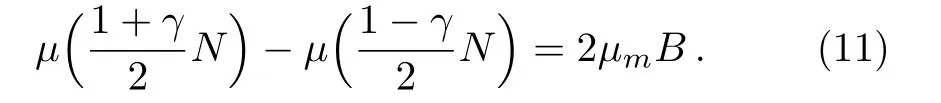
When B=0,we have γ=0,and with small values of B,parameter γ would also be small.Carrying out a Taylor expansion of the above equation at left-hand side about γ=0,we have
i.e.,
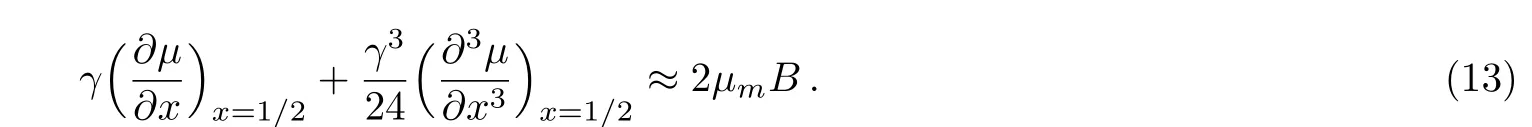
Accordingly,the magnetization is given by
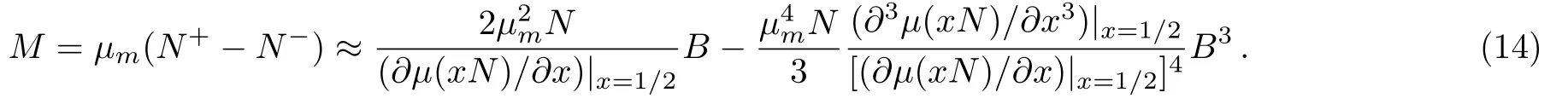
For T→0,the chemical potential of the single-component system can be written as
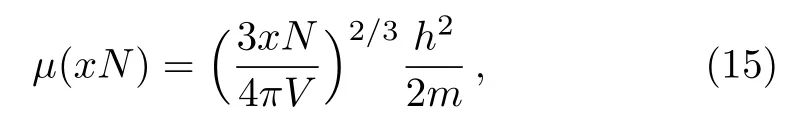
and when B=0,it can be denoted as
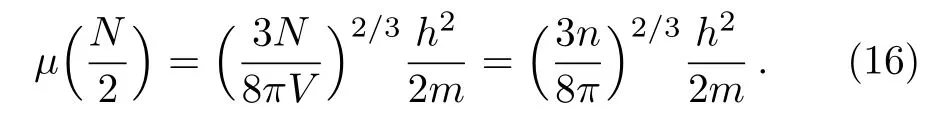
Therefore,the susceptibilities are
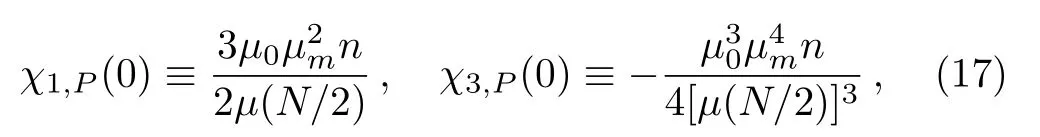
i.e.,
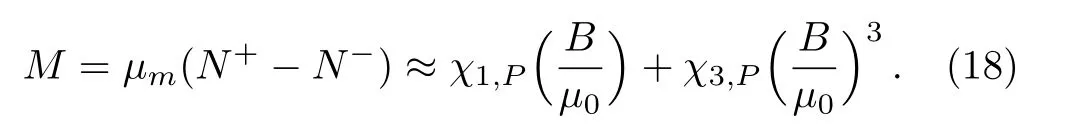
The magnetic field making the third-order correction in Eq.(14)significant is
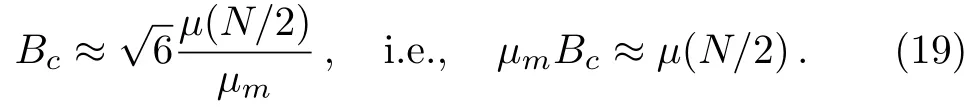
In general,the weak magnetic field can be further quantitatively estimated by
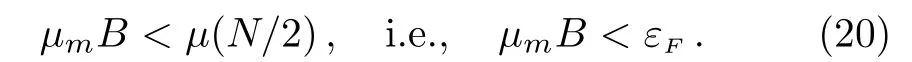
To note that for the free electron gas in copper,we haveμ(N/2)≈ 10?18J.The magnetic field will be extremely high since the density of the electron is too large.On the other hand,with fermionic ultracold atomic gasesμ(N/2)≈ 10?29J.Corresponding to the Fermi temperature of TF~1μK,the magnetic field Bc~1μT.
Now we consider the influence of finite but low temperatures.The chemical potential may be expanded as
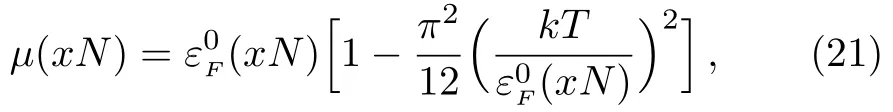
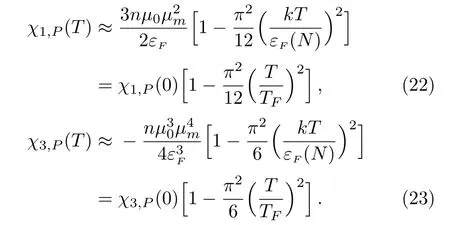
It shows that the third-order susceptibility of Pauli paramagnetism system is diamagnetic.
3 The Third-Order Magnetic Susceptibility of the Landau Diamagnetism System
The Landau diamagnetism arises from the quantization of orbital motion of the charged particles in a plane perpendicular to the direction of the external field.The total energy of the particles is
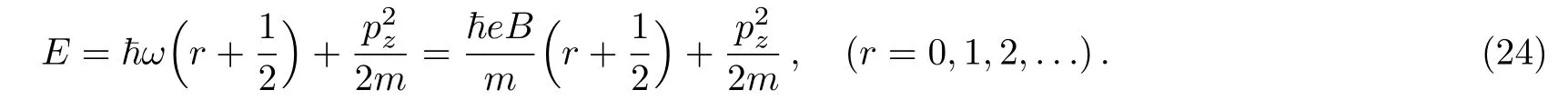
The logarithm of the grand partition function is[1?3]
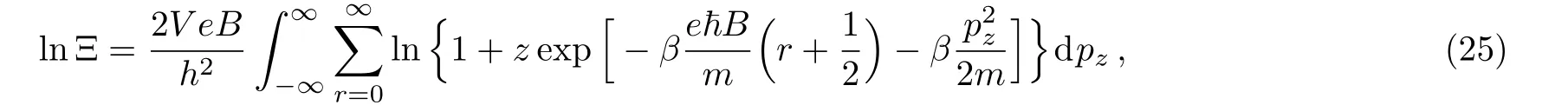
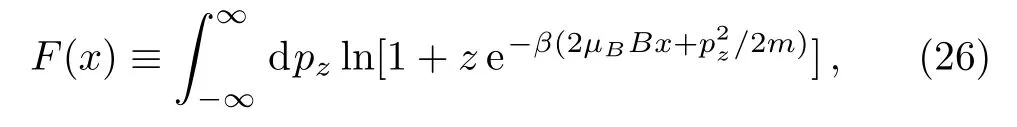
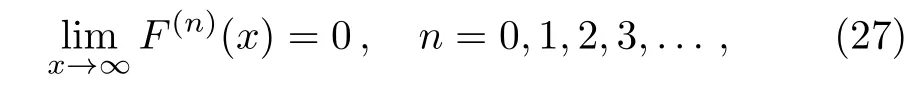
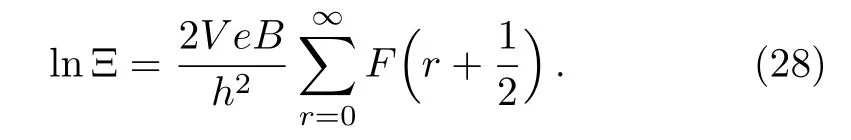
Utilizing the Euler-Maclaurin summation formula,one can prove an approximate result as(c.f.Appendix A)
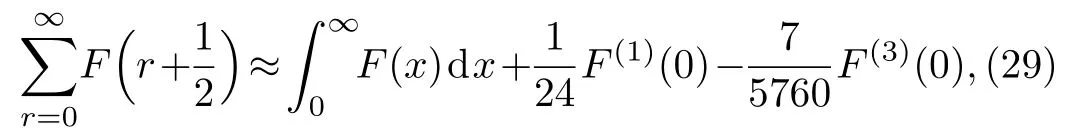
then we have an approximate expression of Eq.(25)as
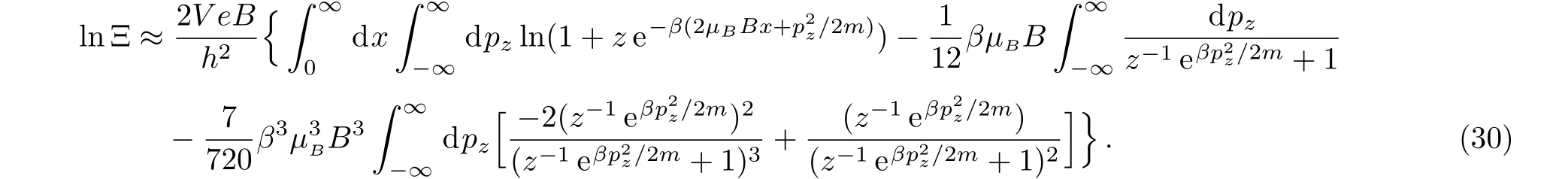
After some computations,we find a much compact expression as(c.f.Appendix B)

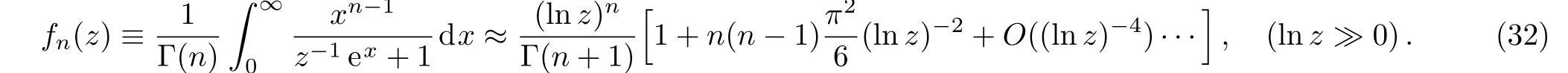
The first term in the right-hand side of Eq.(31)is the standard form of lnfor free Fermi gas without magnetic field,and the second and third term characterize respectively the second and fourth-order correction due to the presence of the weak magnetic field.
Before carrying out the susceptibility,we need to examine how chemical potential depends on both temperature and magnetic field.Since
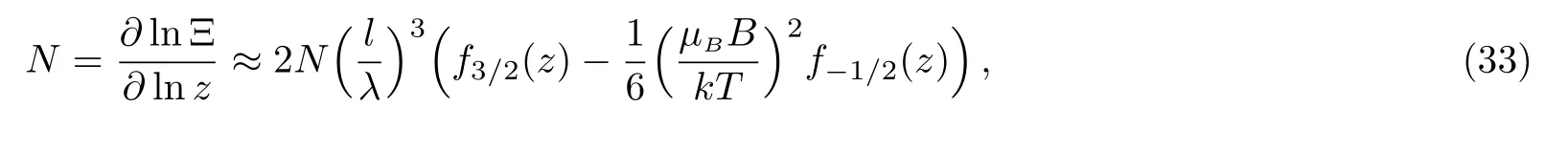
when z is large,i.e.,the temperatures are low,with the use of the approximate expression of Fermi integral when lnz?0,we can reach
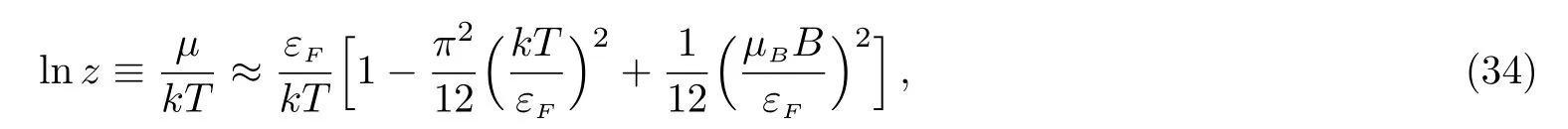
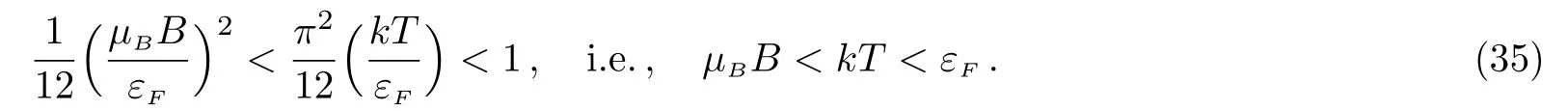
Thus,the influence of the magnetic field on the chemical potential is hereafter ignored,and we have
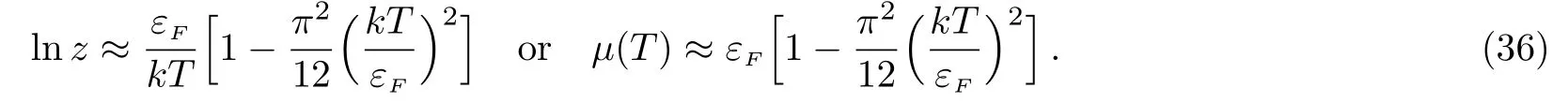
Now we are in position to give the magnetization of the system,which is given by
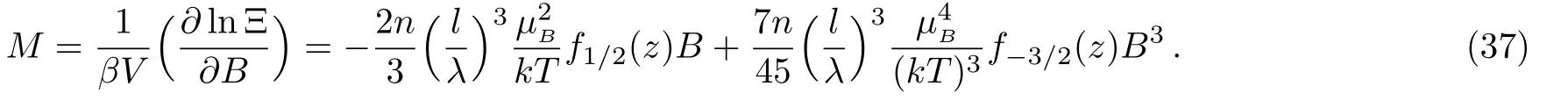
The low- field susceptibilities of the gas are then obtained
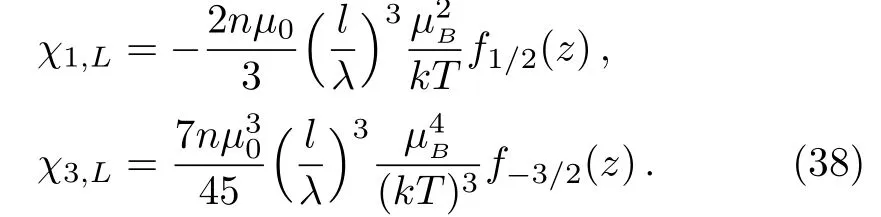
By use of the approximate result of Eq.(36),the susceptibilities can be written as,respectively,
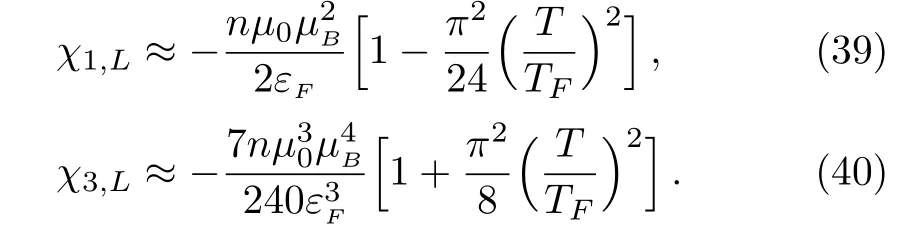
From the above,one can see that the third-order susceptibility of Landau diamagnetism system is also diamagnetic.The magnetic field for which the third-order correction in Eq.(37)cannot be neglected is

It means that the weak magnetic field can be further specified as
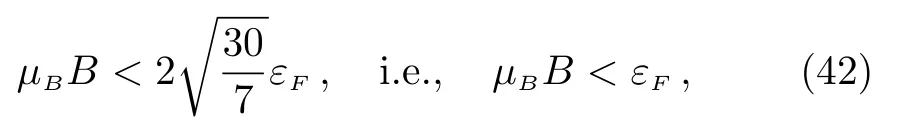
which is compatible with the condition of Eq.(35).
Here,we can see that the finite temperature is one of the origins leading to the breakdown of the 1/3-law,because we have
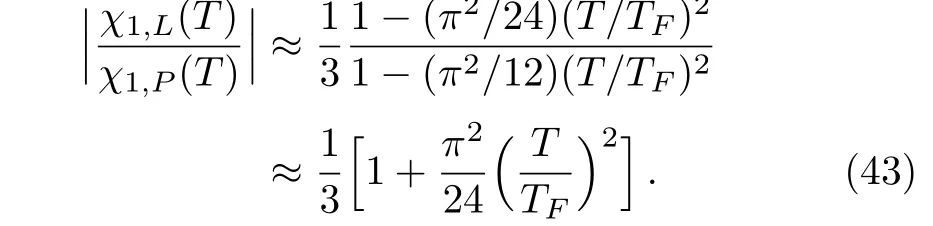
Another origin comes from the third order of the susceptibilities,for we have
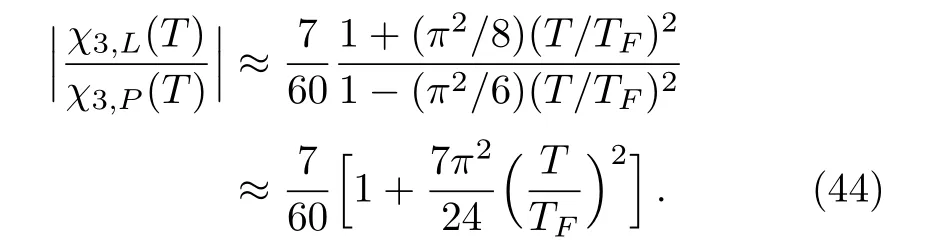
From these two ratios,we see that the orbital motion has less contribution to magnetism than the intrinsic magnetic moment does.
4 The Total Susceptibility
To the lowest order,the magnetization of a free electron gas under weak magnetic field and at low temperature is made up of two independent components:a paramagnetic part due to the intrinsic magnetic moment of the electrons,and a diamagnetic part due to the quantization of the orbital motion of the electrons in the magnetic field.Keeping the magnetic field weak and lowering the Fermi temperature,we find that 1/3-law breaks down,as shown in Eq.(43).Therefore it is worthy of examining the crossing susceptibility additional to the individual paramagnetic and diamagnetic ones.
The electron energy levels now take the following form as[2]
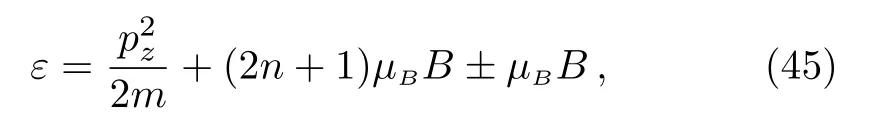
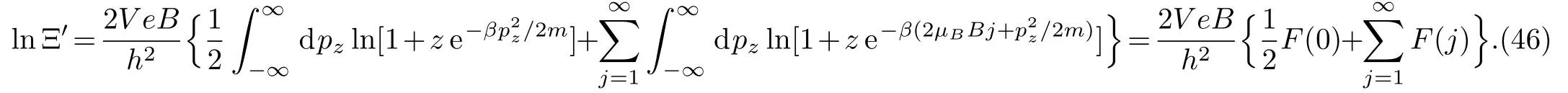
Making use of Eqs.(26)and(29),one can expand lnΞ′to the third order
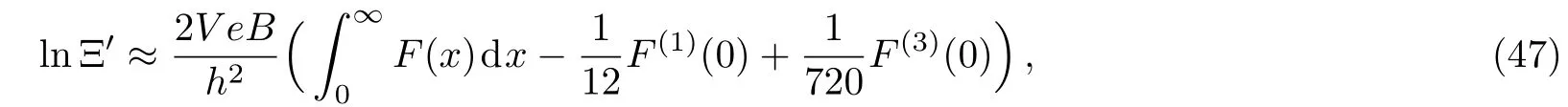
and similarly we obtain the total susceptibilities as,respectively,
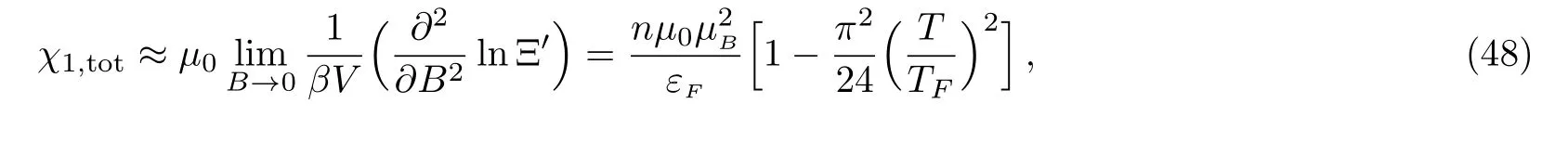
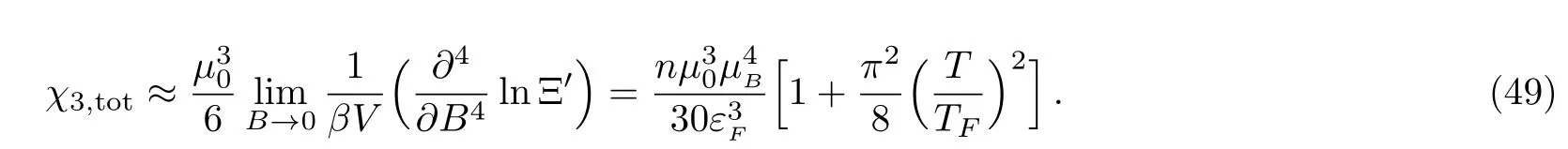
It shows that the system always exhibits paramagnetic property.
Without considering the correction due to the finite temperature(T/TF)2,we recover the well-known result as that given by the 1/3-law,as expected.Once the correction of the finite temperature is taken into account,the system still behaves paramagnetically from Eq.(48),and the crossing susceptibility is also paramagnetic
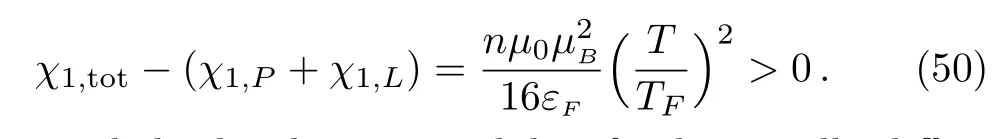
The total third-order susceptibility fundamentally differs from the individual paramagnetic and diamagnetic parts for it is paramagnetic,but they are diamagnetic if viewed individually
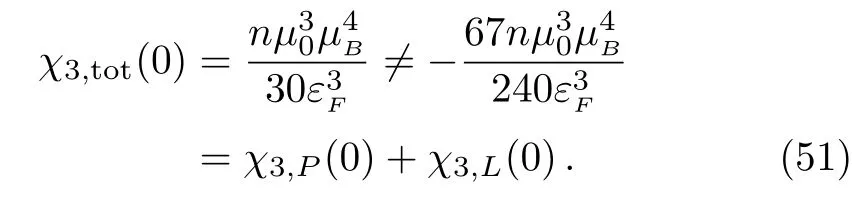
It remains so when finite temperature correction is considered.
5 Discussions and Conclusions
Pauli paramagnetism and Landau diamagnetism are not only common topics in the traditional statistical and condensed matter physics,but also important subjects in modern ultracold atom physics.The principal goal of present study is to give the third-order magnetic susceptibility of an ideal Fermi gas in three cases,individually and in total.We find an interesting property in third-order magnetic susceptibilities:when viewing individually,they are both diamagnetic,but in total it is paramagnetic.For a rough comparison of our results with the experimental one,we mention the recent work[6]of trapped ultracold atoms6Li,which shows that along with the increase of the effective magnetic field,slop of the susceptibility becomes smaller and smaller,even at weak magnetic field.It indicates that the third-order susceptibility is diamagnetic,compatible with our result.
Though the interaction between particles is controllable and has crucial influence on the magnetic property,it is absent from our current treatment.We hope to deal with it in separate works.
Appendix A Derivation of Eq.(29)
The Euler-Maclaurin summation formula,accurate up to the third-order term,is[10]
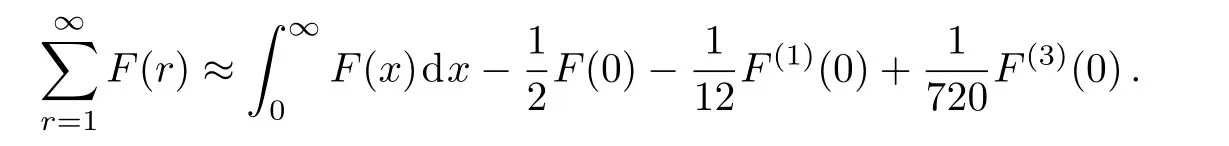
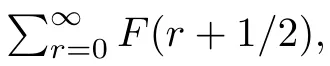
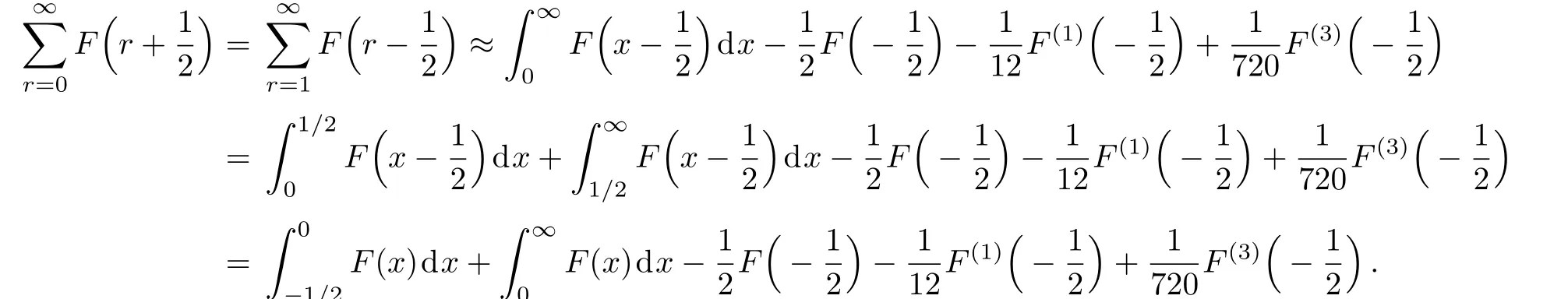
As we see shortly,it is sufficient for our purpose of evaluation of the third-order magnetic susceptibility.For calculation of the integralF(x)dx,we expand F(x)around x=0 and approximate result of this integral turns out to be

Thus,an approximate result for the sum
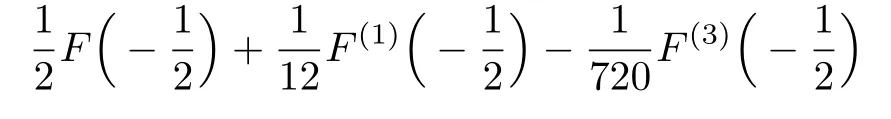
is
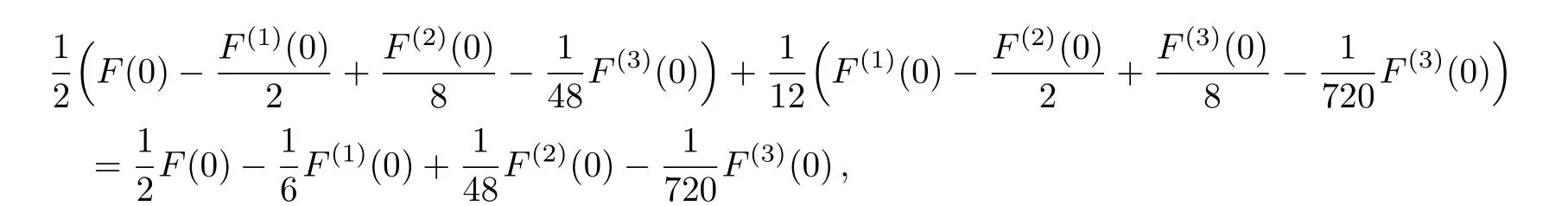
and we obtain
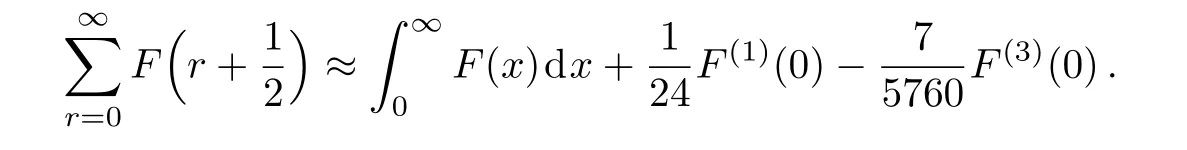
Appendix B An Integral of the Third Term of Eq.(30)
Let G symbolize the third part of Eq.(30),i.e.,
With the substitution pz=y and α = β/2m,the above equation can be rewritten as
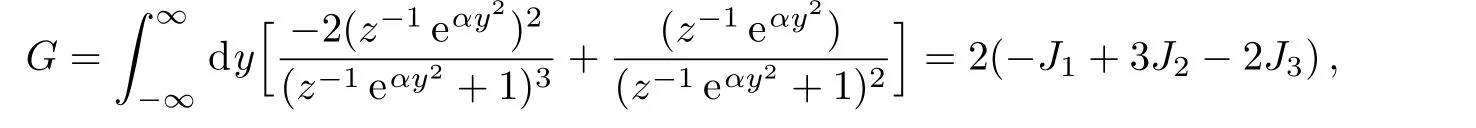
where
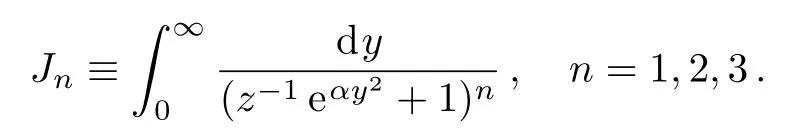
With introducing an integral
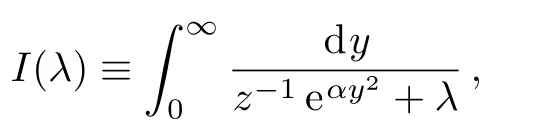
we can obtain
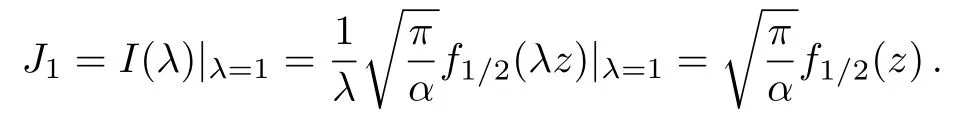
Since the derivative of I(λ)with respect to λ gives
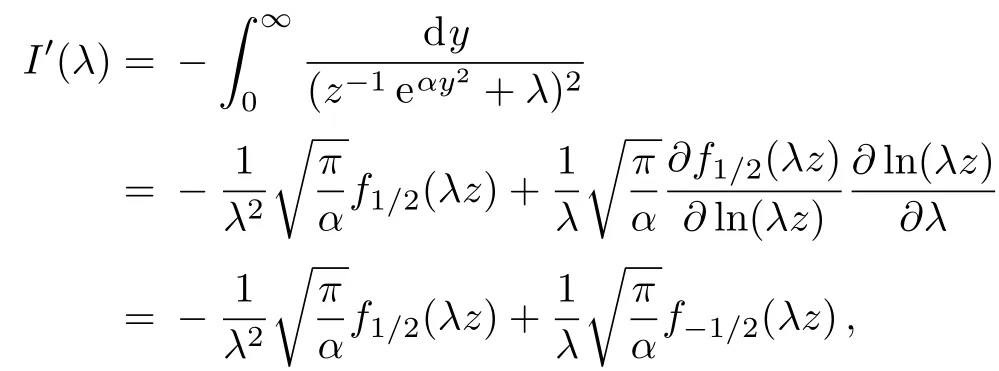
we immediately find
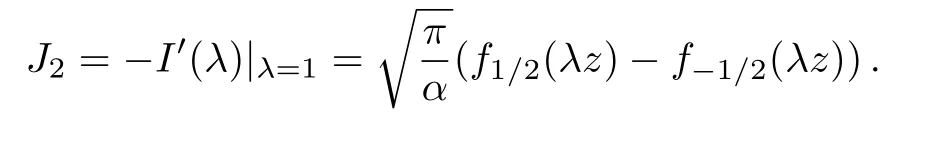
Similarly,we have on one hand
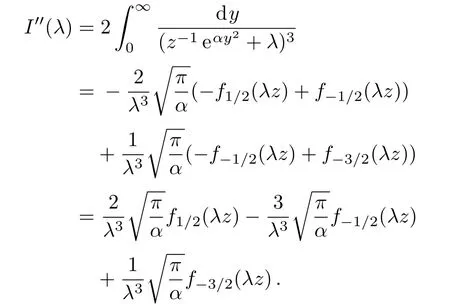
On the other hand,we have
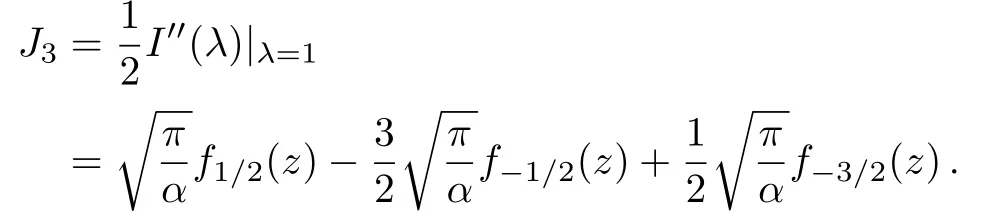
In final,since cancelations among terms,and we obtain a simple result as
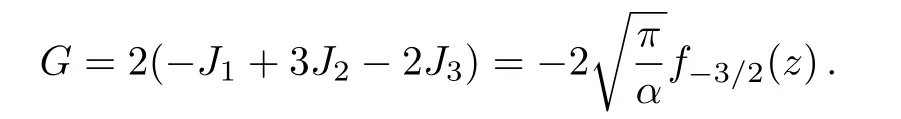
 Communications in Theoretical Physics2018年11期
Communications in Theoretical Physics2018年11期
- Communications in Theoretical Physics的其它文章
- Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects?
- Hierarchical Human Action Recognition with Self-Selection Classifiers via Skeleton Data?
- Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer?
- Coherent Control of the Hartman Effect through a Photonic Crystal with Four-Level Defect Layer?
- Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas?
- Relic Density of Asymmetric Dark Matter in Modified Cosmological Scenarios?
