Coherent Control of the Hartman Effect through a Photonic Crystal with Four-Level Defect Layer?
Feng-Lian Hu,Fazal Badshah,,2,? Abdul Basit,Hai-Yang Zhang,Qing He,,3and Guo-Qin Ge,?
1School of Physics,Huazhong University of Science and Technology,Wuhan 430074,China
2Quantum Optics Lab.Department of Physics,COMSATS Institute of Information Technolgy,Islamabad,Pakistan
3College of Science,Zhongyuan University of Technology,Zhengzhou 450000,China
AbstractIn this paper,we examine the transmission of a probe field through a one dimensional photonic crystal(1DPC)when the sixth layer of the crystal is doped with four level atoms.We analyze effects of the external driving field on the passage of weak probe field across the photonic crystal.It is found that for the phase time delay of the probe photons,intensity of the driving field switches the Hartman effect from sub to superluminal character.It is interesting to note that in our model,the superluminal transmission of the probe pulse is accompanied by a negligibly small absorption of the incident beam.It ensures that the probe field does not attenuate while passing through the photonic crystal.A similar switching of the Hartman effect may be obtained by adjusting detuning of the probe field related to the excited states of the four-level doping atoms.
Key words:phase time delay,photonic crystal,Hartmann effect,superclassicality
1 Introduction
Photonic crystals(PCs)are periodic dielectric media with some exceptional electromagnetic(EM)properties.The most striking feature of these materials is their bandgap structure(BGS)commences due to the interference of light(i.e.,Bragg scattering).Within the photonic band gap(PBG)the electromagnetic field is evanescent.Such an evanescent EM field has an analogy with the electrons in quantum barriers.Therefore,the one-dimensional photonic crystals(1DPCs)act as optical barriers for investigating the tunneling time of the EM signals.[1?2]The tunneling time of a particle through a barrier or the EM wave through an evanescent region has been defined in many ways.[3?8]Amongst all,phase time is the most established both theoretically and experimentally.[9?17]It represents time of traversal of the wave packet through the interaction region and is calculated by employing the energy derivative of the phase of the transmission amplitude.Here we addressed the tunneling time of probe field(photons)through a 1DPC while the tunneling of ultracold atoms(particles)and their superclassical transmission has been studied in some interesting studies.[18?19]
In recent years,the tunneling of EM waves through 1DPCs has attracted many groups of the researchers.This multi-layered arrangement has novel applications in the field of light-matter interaction.[1?2,20?22]According to the Hartman discovery,for long enough barriers,the tunneling time becomes independent of the barrier’s length.[4]It implies superluminal and arbitrarily large group velocities inside long barriers.Since after its recognition,this important effect has been studied extensively in many different systems.[23]The presence of a defect layer in 1DPCs facilitates in providing a coherent control of the Hartman effect of the probe light by controlling susceptibility of the doping atoms in the defected layer.Similarly,the superluminal transmission of the probe field through 1DPCs for two and three level atomic doping have been analyzed in some interesting studies.[24?25]In a recent study,the effects of phase control on the Hartman effect was discussed in the presence of multiple driving fields.[26]
Atomic coherence and quantum interference play a crucial role in controlling the absorption and dispersion nature of the atomic media.In this scenario,the double electromagnetically induced transparency in an inverted-Y-type atomic system with Zeeman sublevels was investigated where it was found that the Zeeman degeneracy of the dark states may be lifted by the increasing intensity of the dressing field.[27]Similarly,the laser-induced atomic gratings may be used to study various characteristics of the stable multicomponent vector solitons consisting of two perpendicular four-wave mixing(FWM)dipole components.[28]Likewise,Zhang et al. experimentally studied PT-symmetric optical lattices with controllable gain-to-loss ratio in a coherently prepared N-type atomic ensemble.The relevant index modulation and the antisymmetric gain and loss pro files were introduced by exploiting the modified absorption and Raman gain in the four-level atomic configuration.[29]Further,interference of the three coupling fields have been used for splitting energy levels periodically,to form a periodic refractive index structure with honeycomb pro file that can be adjusted by the system’s controlling parameters.[30]
Modification of the absorption and transmission characteristics of the atomic medium due to the quantum coherence and interference may lead to the subluminal and superluminal light propagation. It is quite well known that the super and subluminal propagations of light are due to the anomalous and normal dispersions,respectively.[31?33]It has been shown that for anomalous dispersions the group velocities of EM pulses may be abnormal,i.e.greater than c(the speed of light in vacuum),or even becomes negative.[32,34]It has many potential applications in various fields like the all-optical routing,[35?36]all-optical switching,[37]optical memories,and interferometry.[38?39]Here we use intensity of the external driving field to change the dispersion and absorption properties of 1DPC,which further control the phase time delay and the Hartman effect related to the probe field transmission.
In this paper,we study transmission of the probe field through a one-dimensional photonic crystal.We consider that the sixth layer of the photonic crystal serves as a defected layer due to the doping of four-level atoms,which modifies response of the medium to the incident probe field in a similar fashion to the earlier studies related to the absorption and dispersion characteristics of the atomic media.[27?30]By analyzing the tunneling time of transmission,we find that a superluminal propagation of the probe field may be obtained by controlling intensity of the external driving filed.It is noted that the phase time delay saturates with the increasing stack number of the photonic crystal and thus the Hartman effect may be realized for the probe field propagation.Our results show that a proper adjustment of the driving field provides a switching of the Hartman effect from sub to superluminal character.It is interesting to note that here the superluminal transmission of the probe pulse is obtained for a negligible absorption of the probe field,which is always desirable in an experimental treatment.In addition,we show that detuning of the probe field also affects behavior of the phase time delay and causes a switching of the Hartman effect from positive to negative values.
2 Model and Dynamics
Our model consists of a one-dimensional photonic crystal made up of dielectric layers with structural sequencing as(ab)NLa.Here the symbols “a” and “b” are the two different layers of the dielectric material.We take“a” to be the titanium oxide with an index of refraction na=2.22,while “b” is the fused silica with an index nb=1.41.The notation NLstands for the stack number which gives periodicity of the 1DPC and is a measure of its length.The two types of layers satisfy the conditioni.e.they have equal optical thickness.Here λ0is the mid-gap wavelength of the probe field which we have taken as 692 nm,while,is the corresponding frequency with c being the speed of light in free space.The over all structure of the 1DPC is characterized by the sequence of layers(ab)2aD(ab)NLa with D as the defected layer doped with four-level atoms.

Fig.1 (Color online)Schematics of the 1DPC with defect layer.The level structure shows an EIT configuration of the atoms doped in the defect layer D.
Here our aim is to analyze propagation of the probe field through the 1DPC whose sixth layer is doped with a four-level atomic system as shown in Fig.1.In the atomic configuration studied here,there is a coherent driving field ?,which drives the two excited levelsand couples them to level?with detuning?jwith j=1,2 such that,where ν is the frequency of the driving field.The probe field of frequency νpcouples the two excited levels with the lower ground statehaving a detuning δ= ωe1g2? νp.The decay rates from the three upper levels to the ground state|g2?are denoted as γ1,γ2,and γ3,respectively.
There is vacuum at the two ends of the 1DPC and a normal incidence of the probe field is considered for its transmission through the crystal.Using the transfer matrix approach,the electric and magnetic field components at the two nearby positions z and z+?z in a certain layer can be found as[24]
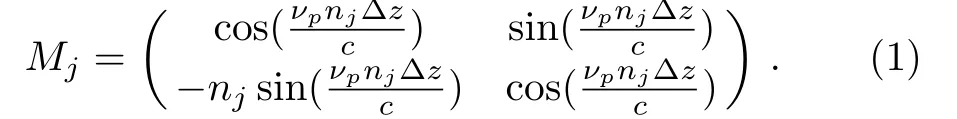
In Eq.(1)njis a function of νpand represents the refractive index of the j-th layer.The transmission coefficient t(νp)corresponding to the incident probe field tunneling through the 1DPC can be calculated as[40?41]
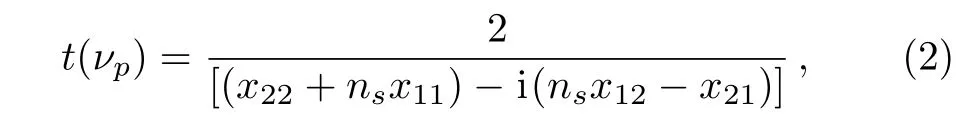
where,xij(i=1,2;j=1,2)are the matrix elements of∏that represents the total transfer matrix connecting the fields at the entrance and exit of the photonic crystal.The parameter nsis the refractive index of the substrate,which is taken to be the free space in our case.The transmission coefficient is a complex quantity,i.e.therefore,the phase time relation for the transmitted probe pulse can be given as[42]
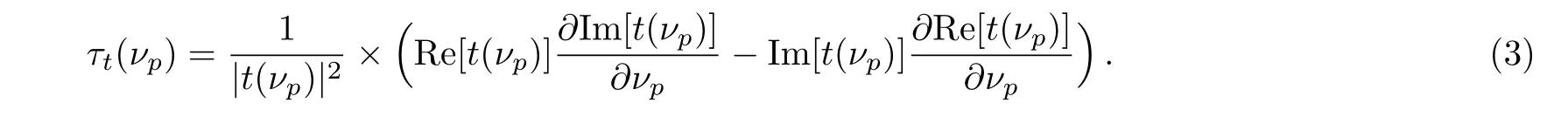
It clearly depends on the real and imaginary parts of the transmission amplitude.
In order to analyze the probe field transmission,we must have an explicit expression for the susceptibility χ of the atomic system,which gives the steady state response of the atoms to the applied field.Solving the density matrix equations of motion at the steady state lead to the dispersion and absorption spectra,which are determined by the real and imaginary parts of the susceptibility[43]
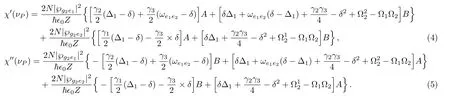
Here N is the atomic density while?g2e1and ?g2e2are the induced atomic dipole moments related to the transition fromrespectively.Similarly,?0is the dielectric constant of free space and ?1and ?2are the Rabi frequencies of the driving field corresponding to the transition?andrespectively.Further,ωe1e2is the energy gap between the two excited levels and the parameter Z is defined to be Z=Y Y?,with Y=A+iB,such that

The dielectric function of the doped layer D can be defined as ?(ω)= ?B+ χ,whereis the background dielectric constant.The optical thickness of layer D is considered aswith nD=1+2πRe[χ]+being the group index which clearly depends on the dispersive properties of the defect layer D.
3 Results and Discussion
For our numerical results,we assumeand take.Frequency of the probe field corresponding to the energy gape between the two excited states and the ground level is chosen to be νp=105γ.In order to discuss the dispersion and absorption characteristics of our system,we plot the real(solid curve)and imaginary(dashed curve)parts of the susceptibility versus the driving field for zero detuning of the probe field.Here we select the driving field such that ?1= ?2= ? and other parameters as γ1= γ2=3γ,γ3=0,?1=0.2γ,ωe1e2=0.4γ.It is noted that behavior of the dispersion curve is normal for smaller values of the driving field as indicated by the solid blue curve of Fig.2.For the given values of the parameters such a behavior remains unchanged for the driving field around ? =0.5γ.It is a mater of fact that the normal dispersion corresponds to the subluminal transmission of the probe field,which is accompanied by large absorption as given by the dashed curve for the smaller values of ? in the given plot.As the driving field increases beyond ? =0.5γ,the normal character of the dispersion changes into the anomalous behavior,which is a sign of the superluminal passage of the probe field through the 1DPC.It is very interesting that for our system the superluminal transmission may be achieved with a negligible absorption of the probe field.Next,in Fig.3,we show the phase time delay of the incident probe field versus the stack number NLfor zero detuning δ.The other important parameters are γ1= γ2=3γ, γ3=0,?1=0.2γ,ωe1e2=0.4γ.When there is no driving fields i.e.?1= ?2=0,we obtain a positive character of the Hartman effect(see Fig.3(a)).Initially,the phase time delay increases as we increase the number of stacks NL.For NL=9 it reaches to a saturated value 1.0×10?29and stays there for further higher values of NL.In the inset of this figure,we have given a plot of the real and imaginary components of the susceptibility χ.The solid blue curve shows that at δ=0,the probe field has a normal dispersion(positive slope)and the corresponding phase time is positive.Therefore,a subluminal Hartman effect is realized for the parameters of Fig.3(a).The dashed red curve of the insets has high values,which indicates that here the subluminal Hartman effect corresponds to a higher absorption of the probe field.For a small driving field of magnitudes ?1= ?2=0.02γ,the saturation point of the phase time delay occurs at a bit higher value tphase=1.15× 10?29,which shows its sensitivity to the applied driving field.
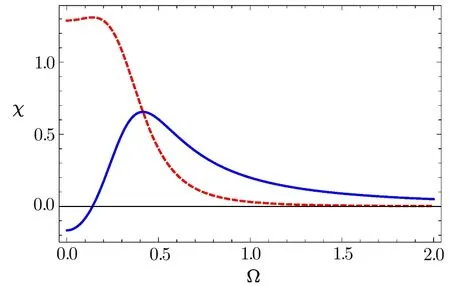
Fig.2 (Color online)Real(solid curve)and imaginary(dashed curve)parts of the susceptibility(χ)as a function of the driving field ? for δ=0 and ?1= ?2= ?.Other parameters are γ1= γ2=3γ,γ3=0,?1=0.2γ,ωe1e2=0.4γ.
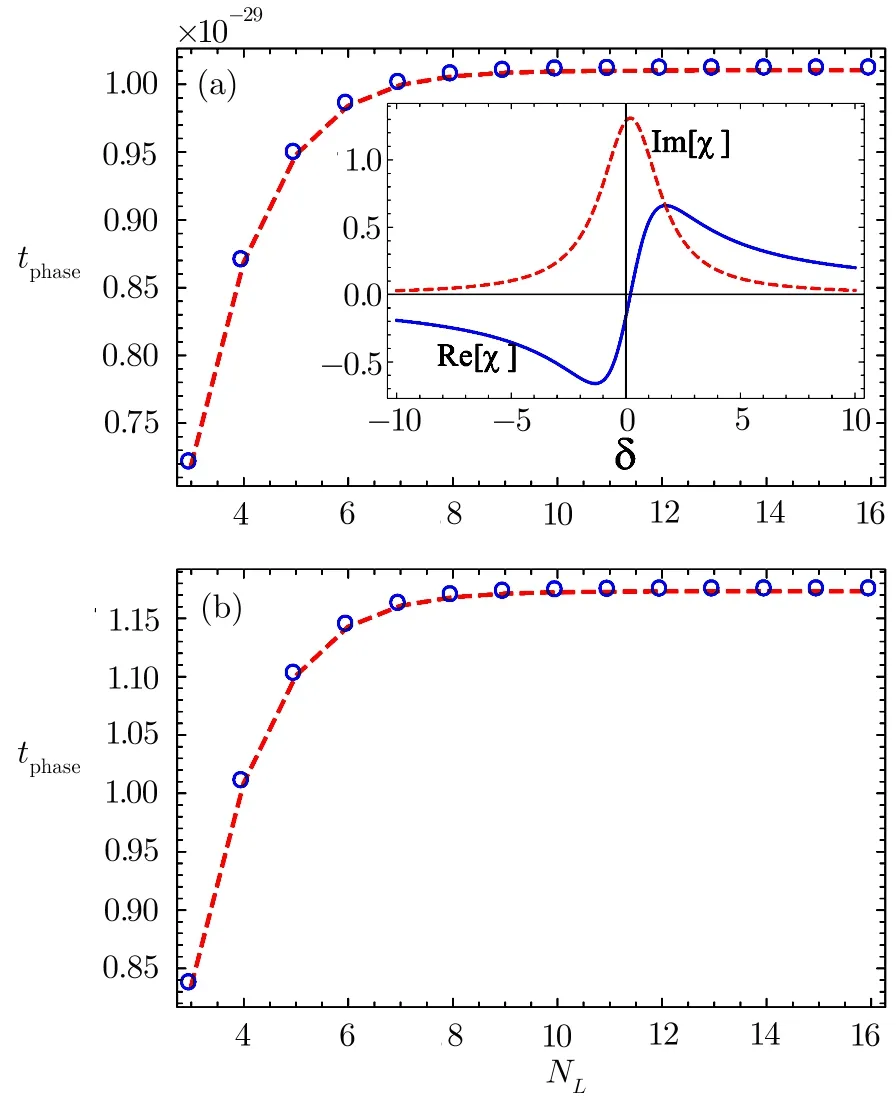
Fig.3 (Color online)Phase time delay tphasevs.number of stack NLfor(a)?1= ?2=0,(b)?1= ?2=0.02γ.Other parameters are γ1= γ2=3γ,γ3=0,?1=0.2γ,ωe1e2=0.4γ.
When we further increase the applied driving field to a strength ?1= ?2=2γ,anomalous dispersion at δ=0 is obtained as shown by the real component of susceptibilityin the inset of Fig.4(a).The main plot in this figure is the phase time delay as a function of the stack number of the 1DPC at δ=0.Here phase time of the probe field through the photonic crystal is negative or superluminal.For this case,we again obtained a saturation value of the phase time delay,which remains static with further increments in the stack number.It means that for the current value of the driving field(?1= ?2=2γ)negative Hartman effect is realized for a 1DPC constituted by the two positive refractive index materials(PIMs).Thus the intensity of the applied driving field plays a crucial role in changing the dispersive nature of the photonic crystal for the passage of the incident probe field.Consequently,a proper choice of the driving field intensity enables us to switch from positive to negative Hartman effect.Another important feature is the correspondingly effectively no absorption of the probe field for the parameters used here(see the dashed red curve(Im[χ])in the inset of Fig.4).It is a matter of great concern that for our system we obtained superluminal transmission of the probe field with a negligible absorption.This ensures a smooth passage of photons through the crystal without any considerable attenuation of the incident beam.This provides an edge to our model over various studies where the superluminal transmission was found with high gain[44]or absorption.[45]
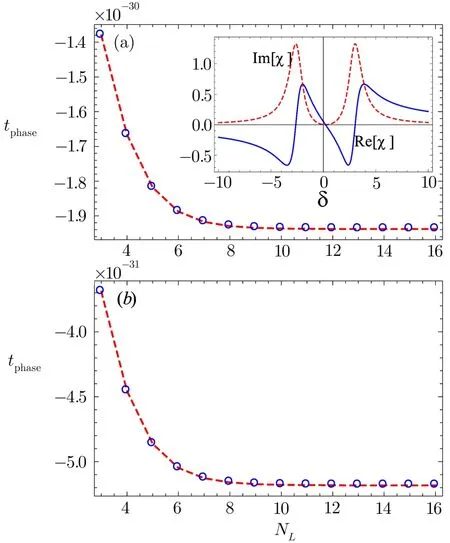
Fig.4 (Color online)Phase time delay tphasevs.number of stack NLfor(a)?1= ?2=2γ,(b)?1= ?2=4γ.Other parameters are γ1= γ2=3γ,γ3=0,?1=0.2γ,ωe1e2=0.4γ.
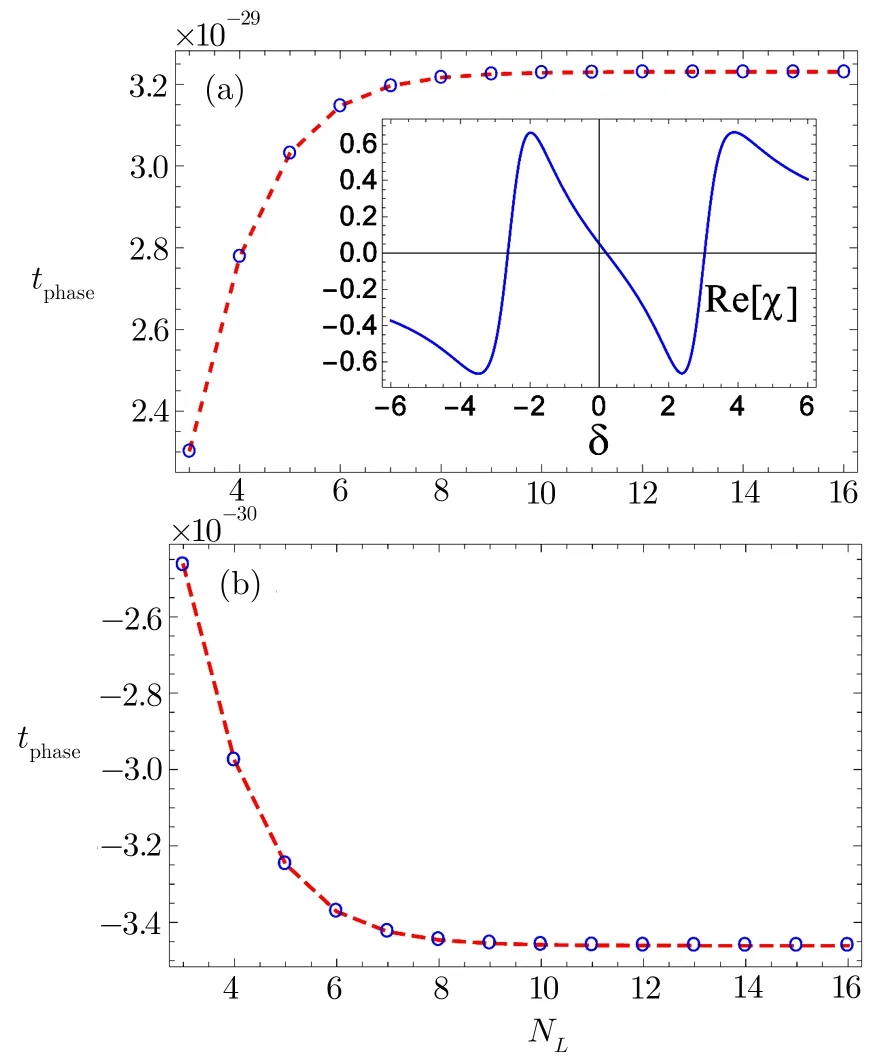
Fig.5 (Color online)Phase time delay tphasevs number of stack NLfor the parameters in Fig.3(a)with detuning(a)δ=?3.0γ and(b)δ=1.0γ.
Further,we show a switching of the Hartman effect from sub to superluminal character by the atom- field detuning for a constant driving field(?1= ?2=2γ).In Fig.5(a),we select detuning as δ= ?3.0γ and plot the phase time delay as a function of the stack number NL.Rest of the parameters are the same as used in Fig.4(a).It can be seen from the dispersion curve of the probe field(inset of Fig.5(a))that its behavior at δ= ?3.0γ is normal i.e.the slope of the curve is positive.As the normal dispersion results the subluminal transmission that is why here we obtain a positive(subluminal)Hartman effect with a saturation value around tphase=3.25×10?29.In Fig.5(b)we choose a different value of detuning of the probe field i.e.δ=1.0γ for which the phase time delay gets superluminal values against increasing stack number of the photonic crystal.Here the saturation occurs at tphase= ?3.45× 10?30(a superluminal value)as indicated by the anomalous dispersion at the present value of detuning(see inset of Fig.5(a)).Therefore apart from the intensity of the driving field the atom- field detuning also provide a switching from the sub to superluminal Hartman effect for the probe field transmission.
In summery,here we have proposed a scheme in which an incident probe field interacts with a 1DPC having a defect layer due to four-level atomic doping.The photonic crystal is made up mainly of two positive index materials with a slight doping in the sixth layer of the multilayered arrangement.This causes a remarkable change in the dispersion and absorption characteristics of the photonic crystal.Here we find that by controlling the Rabi frequency of the external driving field one can change the phase time delay of the probe field from sub to superluminal behavior.It is noted that for a suitable values of the parameters the superluminal character of Hartman effect may be obtained for a negligible absorption of the incident beam,which is always desired in an experimental treatment.The probe field detuning also provides a switching of the Hartman effect from positive to negative nature.
 Communications in Theoretical Physics2018年11期
Communications in Theoretical Physics2018年11期
- Communications in Theoretical Physics的其它文章
- Numerical Study of Unsteady MHD Flow and Entropy Generation in a Rotating Permeable Channel with Slip and Hall Effects?
- Hierarchical Human Action Recognition with Self-Selection Classifiers via Skeleton Data?
- Spin Thermoelectric Effects in a Three-Terminal Double-Dot Interferometer?
- Third-Order Magnetic Susceptibility of an Ideal Fermi Gas?
- Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas?
- Relic Density of Asymmetric Dark Matter in Modified Cosmological Scenarios?
