Ying Zhou,Quansen Sun?,Jixin Liu

1School of Computer Science and Engineering,Nanjing University of Science and Technology,No.200 Xiao Ling Wei Street,Nanjing,People’s Republic of China

2Research Center of Wideband Wireless Communication Technology,Nanjing University of Posts and Telecommunications,Nanjing,People’s Republic of China

?E-mail:sunquansen@njust.edu.cn

Abstract:The measurement matrix which plays an important role in compressed sensing has got a lot of attention.However,the existing measurement matrices ignore the energy concentration characteristic of the natural images in the sparse domain,which can help to improve the sensing efficiency and the construction efficiency.Here,the authors propose a simple but efficient measurement matrix based on the Hadamard matrix,named Hadamard-diagonal matrix(HDM).In HDM,the energy conservation in the sparse domain is maximised.In addition,considering the reconstruction performance can be further improved by decreasing the mutual coherence of the measurement matrix,an effective optimisation strategy is adopted in order to reducing the mutual coherence for better reconstruction quality.The authors conduct several experiments to evaluate the performance of HDM and the effectiveness of optimisation algorithm.The experimental results show that HDM performs better than other popular measurement matrices,and the optimisation algorithm can improve the performance of not only the HDM but also the other popular measurement matrices.

1 Introduction

Compressed sensing(CS),a theory which was proposed by Candès[1]and Dohono[2],seeks to reconstruct a sparse signal from a small number of linear measurements efficiently.In CS,the sparsity is an essential requirement for the signals;however,it is not sufficient for a signal to be reconstructed successfully.Choosing a suitable measurement matrix is especially important in CS which ensures an exact recovery of the signal from the linear measurements with high probability.Over the past few years,a great deal of measurement matrices have been proposed.From the perspective of construction,these matrices can be divided into two categories:the random matrix and the deterministic matrix.Gaussian random matrix[3]and Bernoulli matrix[4]are typical random matrices,which are proved to be satisfied with the restricted isometry property(RIP)at the earliest and have a good performance during the simulation process.The performance of dense matrix is limited by the high computation cost and the huge storage space.To alleviate the problem,the sparse random matrix[5]was proposed where most elements are ‘0’just few ‘1’,which makes the computation cost lower and the space storage fewer.However,the random structure is hard to be implemented in hardware.Hence,the sparse binary but deterministic matrix is proposed.The sparse binary but deterministic matrix is the ideal measurement matrix for the hardware implementation.After Dimakis and Vontobel[6]indicated the tight connection between the channel coding and the CS,various channel coding matrices are applied in CS as the measurement matrix,such as the low-density parity check(LDPC)code[7],the Toeplitz circulant code[8],the BCH code[9],and the Hadamard code[10]and so on.These coding matrices are binary and structured,so that it is easy to design them in hardware implementation.However,these matrices still need a lot storage space and all the aforementioned matrices are independent of the signals.What is more,they do not consider of keeping the main information of the signals more to improve the sensing efficiency of the measurement matrix.Hence,how to select a simple but efficient measurement matrix still be an open problem in CS.

In addition,the measurement matrix should have specific properties to ensure a stable reconstruction of the signals in the CS framework.Candès and Tao[11]proposed that the measurement matrix in CS should be satisfied with RIP in order to ensure the accurate reconstruction.Actually,to verify a measurement matrix whether satisfies the RIP or not is an extremely complex and hard problem.Moreover,the RIP is not the necessary condition of the reconstruction problem,just a sufficient condition.Hence,the Donoho[12]proposed that the mutual coherence coefficient of the measurement matrix and the sparse basis can be feasible to measure the reconstruction condition.The smaller the mutual coherence coefficient is,the weaker the correlation of the measurement matrix and the sparse basis is.In addition,Elad[13]proposed the Spark to describe the correlation of the measurement matrix and the sparse basis.Then,Baraniuk[14]claimed that if the measurement matrix is incoherent enough with the sparse basis,the sensing matrix can satisfy the RIP most likely.Hence,reducing the coherence between the measurement matrix and the sparse basis becoming the key of the optimisation for the measurement matrix.Recently,some works are reported to improve the quality of reconstruction by decreasing the mutual coherence.Elad [15]proposed an optimisation algorithm to iteratively decrease the average mutual coherence,which used a shrinkage operation followed by a singular value decomposition(SVD)step.Abolghasemi et al.[16]suggested to segment the input signal and take random samples with different rates from each segment to realise a kind of non-uniform sampling.Duarte-Carvajalino and Sapiro proposed an optimised algorithm with the aim of decreasing mutual coherence based on the SVD.Wang and Arce[17]proposed a variable density sampling strategy by exploiting the prior information about the statistical distributions of natural images in the wavelet domain,which is computationally efficient and can be applied to several transform domains.In another work[18],Wang et al.proposed to generate coloured random projections using an adaptive scheme.Also,Duarte-Carvajalino et al.[19]took the advantage of an eigenvalue decomposition process followed by a KSVD-based algorithm to optimise the measurement matrix and learn dictionary,respectively.Li et al.[20]proposed a gradient descent-based algorithm derived for solving the optimal sensing matrix problem.Cleju [21]proposed a novel formulation in the form of a rank-constrained nearest correlation matrix problem.The results of all previous methods reveal the improved performance which is an evidence of the benefits that optimal sampling can provide for this framework.

Motivated by the above concerns,in this paper,we propose a simple but efficient measurement matrix which is named Hadamard-diagonal matrix (HDM)for CS.Different from Hadamard matrix,in HDM,the elements of ‘-1’are replaced by‘0’because{0,1}coding is more reasonable than the{1,-1}coding during the hardware implementation.What is more,to further enhance the sparsity,the main sensing rows and columns in HDM is fixed by ‘1’,and the others are fixed by ‘0’.Furthermore,adding the energy distribution limitation of the natural images in the sparse domain(the discrete cosine transform(DCT)considered in this paper)can keep more main energy information of the signals after the sampling,which is extremely different from the other constructions for the measurement matrix.Hence,HDM is much sparser than the other sparse binary matrix.

Another contribution in this paper is to apply a novel approach for optimising the measurement matrix.According to the properties of matrix SVD,the smaller the maximum singular value is,the better the matrix incoherent is.Based on which,we improve the incoherence of the HDM in this paper.What is more,our experimental results confirm the robustness of the optimisation method and show that applying this optimisation method helps inreducing the reconstruction error and hence both orthogonal matching pursuit(OMP)and basis pursuit(BP)benefit from this matrix.

Table 1 Abbreviation table

The remainder of the paper is organised as follows:Section 2 introduces the basis theory of CS and the Hadamard matrix.In Section 3,the energy characteristic of the signals in the DCT domain and the HDM are presented.In Section 4,an optimisation strategy for the measurement matrix is presented.In Section 5,comparative experiments are conducted to evaluate the proposed matrix.Section 6 gives the final conclusion.

2 Related works

In the rest of this paper,we reserve normal symbols to scalar variables and boldface symbols to variables for clarity.Table 1 specifies the frequently used variables in this paper.

2.1 Theory of CS

Assume that a signal X∈Rnhave a k-sparse representation in some domain Ψ ∈ Rn×n.It means X= Ψx,and x has only k(k ≤ n)non-zero entries.The sampling process of CS can be expressed as a linear projection

where Φ ∈ Rm×n(m ≤ n)is the measurement matrix,and A= ΦΨ the sensing matrix.The CS focuses on reconstructing the signal X with a small number of measurements,it means finding the sparsest representation of X,namely

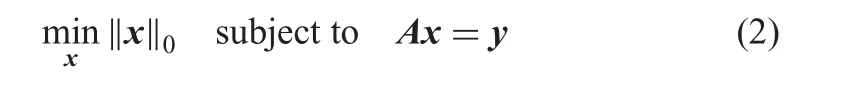
where ‖·‖0is ?0-norm and means the number of non-zero entries of x(Table 2).

However,the ?0-norm problem is an NP hard optimisation.Hence,a lot of greedy algorithms are proposed,such as matching pursuit(MP)[22],OMP[23],regularised orthogonal matching pursuit(ROMP)[24],compressive sampling matching pursuit(CoSaMP)[25],and sparse adaptive matching pursuit(SAMP)[26].Generally,the optimisation problem(2)can also be relaxed as solving the ?1minimisation[27]as follows:

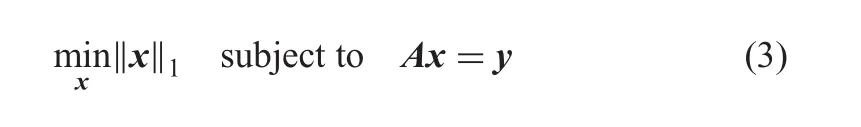
where ‖·‖1is ?1-norm and means the absolute sum of all entries of x.

We can solve the optimisation problem(3)with the BP[11],gradient projection for sparse reconstruction algorithm,least angle regression algorithm,interior point method,and iterative threshold algorithm.In addition,the matrix A should satisfy RIP[14]toguarantee the accurate recovery of the k-sparse signal x from the measurements y

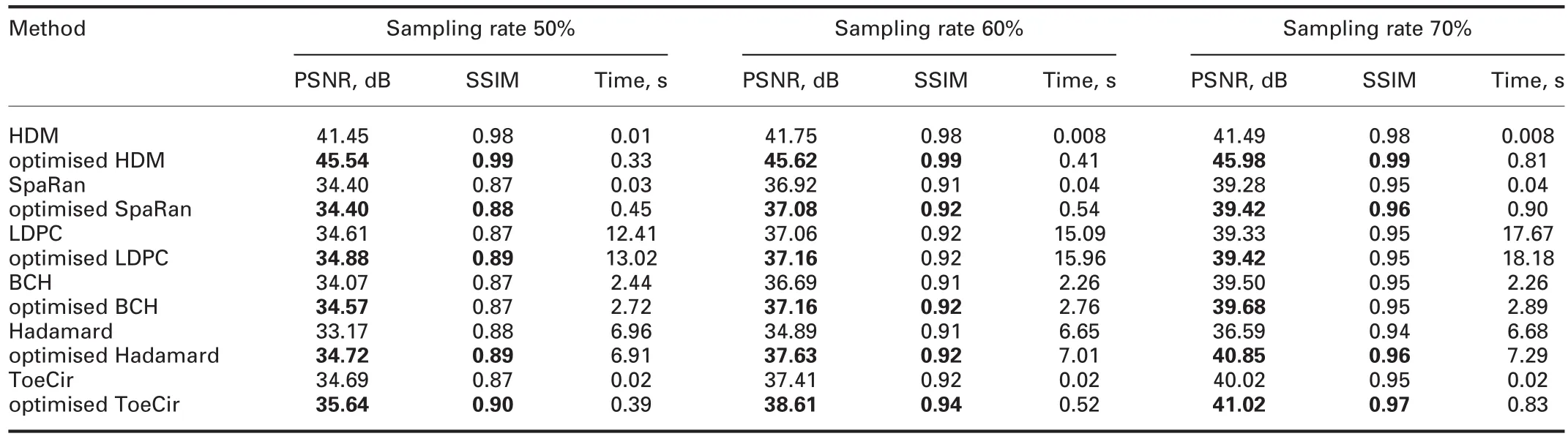
Table 2 PSNR,SSIM,and time of the reconstruction images with different measurement matrices in different sampling rates

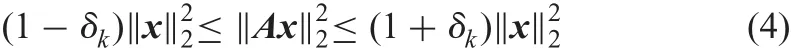
where the parameterδk∈ (0,1).

The coherency measured the measurement matrix and the sparse basis is called ‘mutual coherency’[28]:

The coherence between rows of the measurement matrix,and columns of representing matrix should be as small as possible.In other words,the correlation between any distinct pair of columns in sensing matrix A should be very small,and that means to have an early orthogonal matrix A.It is shown that random matrices with Gaussian[3]or Bernoulli[4]distributions are appropriate choices,as they satisfy this property with high probability and can be generated non-adaptively.

2.2 Hadamard matrix

Hadamard matrix[2]Hnis an n-dimensional square matrix consisting of{1,-1},where n=2l(l=1,2,3,...).Any two rows or columns of the Hadamard matrix are orthogonal,namely

H1=1,and the 2l-dimensional Hadamard matrix is constructed as follows:

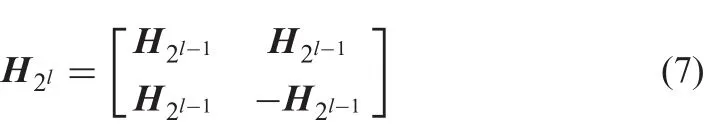
where l=1,2,3,...,and a sample of l=3 is shown as

3 Hadamard-diagonal matrix

The DCT as a mapping for converting a signal into the frequency domain is widely used for CS as the sparse basis.The two-dimensional(2D)version of the DCT for the m×n signal S is given as follows:

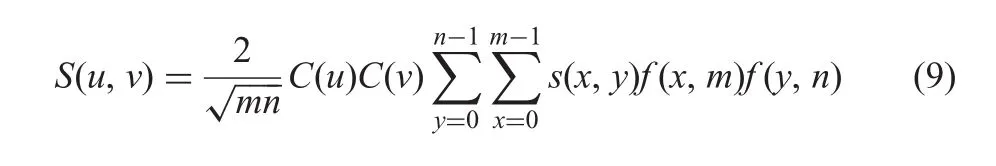
where

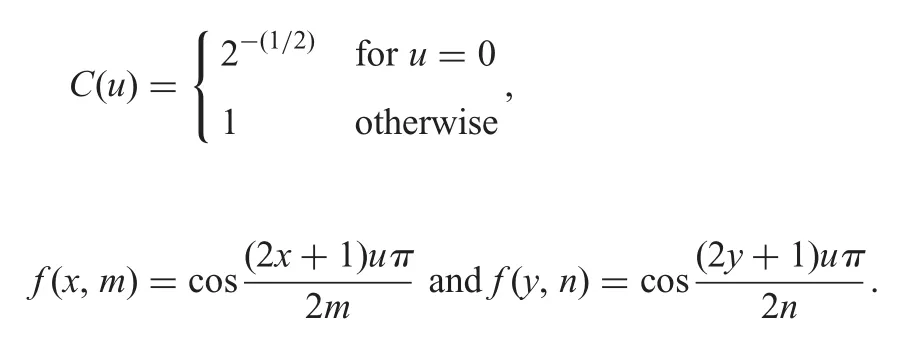
The DCT has a good energy concentration characteristic which means the energy of the signal in the DCT domain concentrated in the upper left of the signal showing as Fig.1.Fig.1a is the natural image Peppers and we can hardly observe its energy distribution.Fig.1b shows us the energy distribution of the Peppers in the DCT domain.The distribution of the energy is measured by the colour bar with the scale from-8 to 10.With the increasing of the scale value,the more energy is contained of the area covered by the colour of which.We can see the energy of the image concentrates in the upper left corner and is divergent shaped from Fig.1b.Generally,the measurements which are sampled in the sparse domain for CS need reserve the energy as much as possible to improve the sensing efficiency and even the reconstruction accuracy.

The Hadamard matrix preforms well in the CS when reconstructing the signals.However,it is dense as the Gauss matrix or the Bernoulli matrix,which requires a lot of storage space and makes the time cost high.What is more,the Hadamard matrix is not conductive to the hardware implementation and promotion.Then the block diagonal Hadamard matrix(BDHM)[10]was proposed by Gan et al.,which is sparser to reduce the storage space and the time cost and which is easier for the hardware implementation.However,it is restricted by the dimension of the matrix,which must be the square of 2.So,the performance of the BDHM is limited.The measurement matrices above-mentioned never consider the energy concentration characteristic in the sparse domain.Hence,we propose a novel measurement matrix,which is called HDM.The HDM considers the energy analysis of the DCT domain which is helpful to improve the sensing efficiency and even the accuracy of reconstruction.Specifically,we construct the HDM based on the Hadamard matrix which only keeps the main sensing rows and columns such as the first row and the first column of the matrix with ‘1’and the others with ‘0’.From Fig.1,we can see the energy of the natural image in the DCT domain is mainly concentrated in the upper left corner with the divergence to the centre sometimes.Then,the elements in diagonal line are set as ‘1’.The construction of HDM is shown as(10).Compared with the BDHM,there is no limitation of dimension in HDM.On the other hand,HDM considers the energy distribution of image.Compared with the Hadamard matrix,HDM is sparser and easier for the hardware implementation

Fig.1 Example natural image

Fig.2 Algorithm 1:The optimisation algorithm for HDM Φ ∈ Rm×n

Fig.3 Experimental natural images

Fig.4 Reconstruction of Lena with the 20%sampling rate and the PSNRs of different measurement matrices

Fig.5 Reconstruction of Lena with the 20%sampling rate and the PSNRs of different measurement matrices

Fig.6 Reconstruction of Lena with the 20%sampling rate and the PSNRs of different measurement matrices

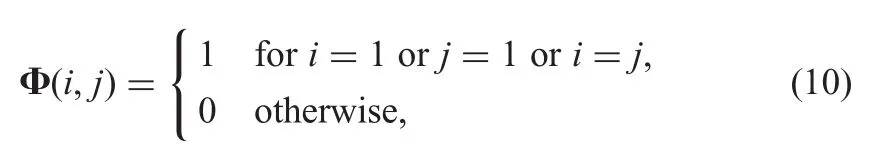
where Φ ∈ Rm×n,i∈ (1,m),j∈ (1,n).

4 Optimisation of the measurement matrix

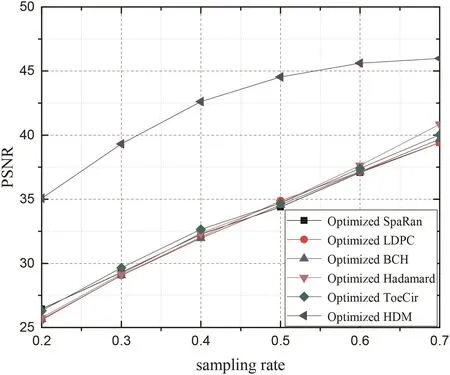
Fig.7 Comparison of reconstruction performance(PSNR)from different optimised measurement matrices versus different sampling rates

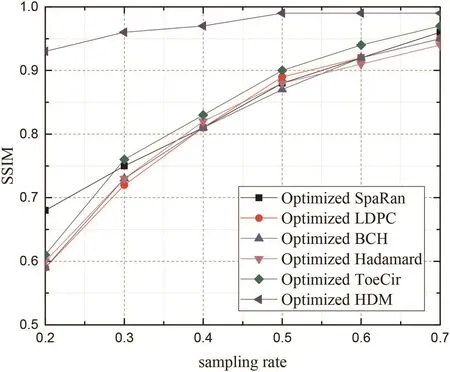
Fig.8 Comparison of reconstruction performance(SSIM)from different optimised measurement matrices versus different sampling rates

In general,the non-zero coefficients of the sparse signal are concentrated in the low-frequency band,while the coefficients of zero or near zero are concentrated in the high-frequency band.Therefore, increasing the measurement coefficient in the low-frequency band of the measurement matrix can obtain more signal information with the same number of samples,so as to reconstruct the original signal more accurately.The measurement matrix retains the most of the coefficients in the low-frequency band to improve the sensing efficiency.However,the incoherence of the measurement matrix is reduced inevitably with the increasing of the coefficients in the low-frequency band of the measurement matrix.According to the properties of matrix SVD,the smaller the maximum singular value is,the better the matrix incoherent is.Based on which,we improve the incoherence of the measurement matrix in this paper.The complete algorithm is summarised as Algorithm 1(see Fig.2).

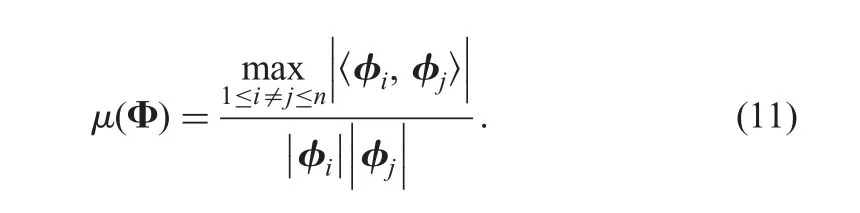
We consider the mutual coherence of the measurement matrix Φ as follows:In general,the smaller the mutual coherence of the matrix is,the more incoherent the matrix is.We aim to reduce the mutual coherence of the measurement matrix.Another way to describe the mutual coherence of the measurement matrix is computing the Gram matrix G=ΦTΦ after normalising each of its columns.The off-diagonal entries in G are the inner products that appear in(11).Then the largest magnitude of the off-diagonal entry Gijis the mutual coherence.

Now,consider the eigen decomposition of Φ which is

where

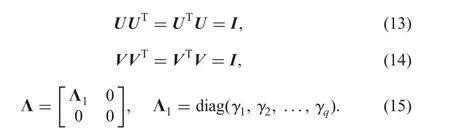
The γ1,γ2,...,γqare the singular values of the Λ and the t-averaged singular value tγof the Λ defined as follows:

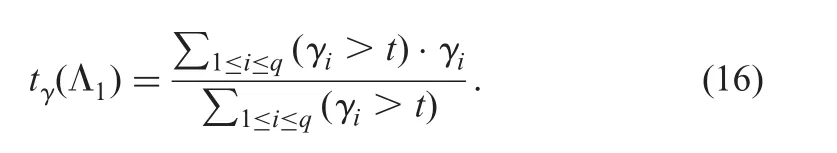
Then the Gram matrix can become

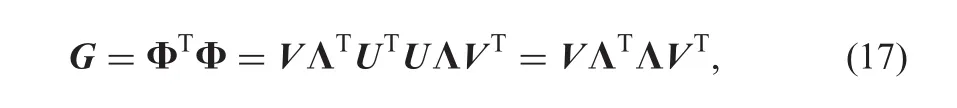
which is equivalent to

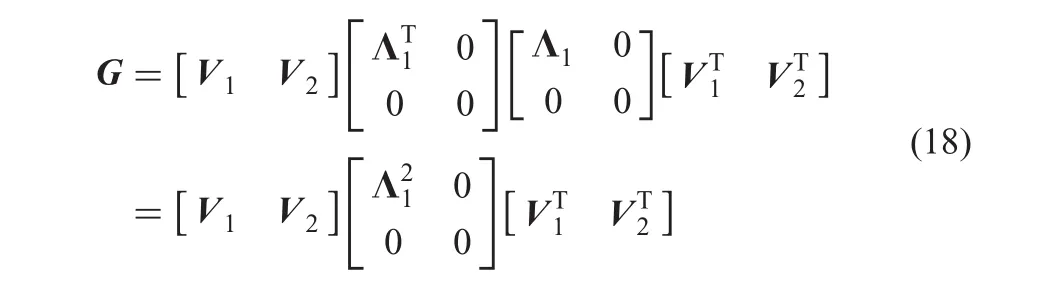
Table 3 PSNR(dB)of the reconstruction of Boat,Baboon,and Peppers images

When Λ1? I and q? n,(17)can be simplified as follows:

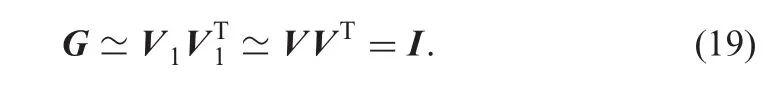
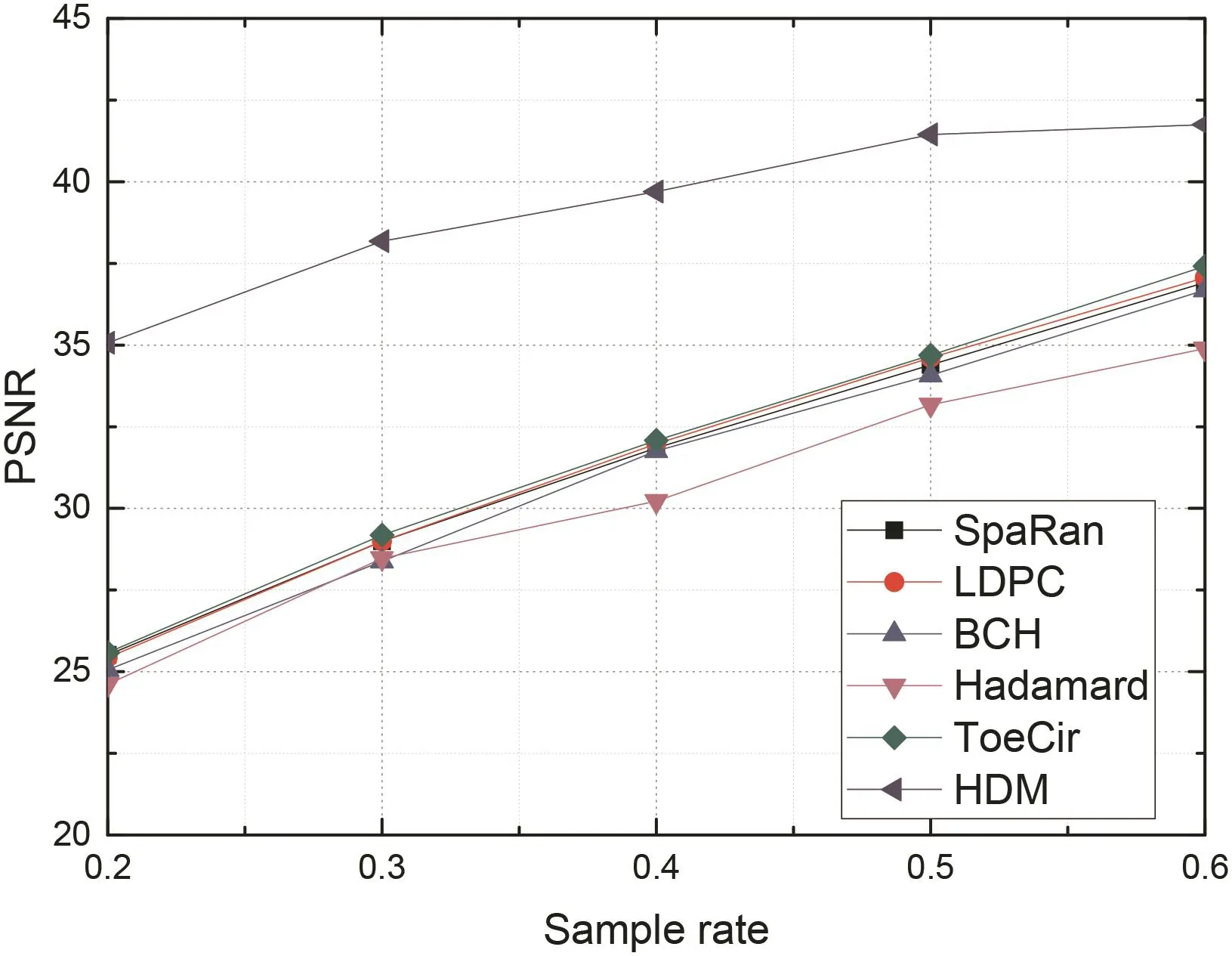
Fig.9 Comparison of reconstruction performance(PSNR)from different original measurement matrices versus different sampling rates

Fig.10 Comparison of reconstruction performance(SSIM)from different original measurement matrices versus different sampling rates

Table 4 PSNR(dB)of the reconstruction Peppers image

The matrix G is infinitely close to the identity matrix,which means the largest magnitude of the off-diagonal entry Gijis close to 0.Moreover,the optimisation method reduces the mutual coherence of the measurement matrix significantly but also keeps high sensing efficiency.In addition,the experimental results show that the measurement matrix with modified singular value has better RIP properties and the reconstruction effect is obviously improved.

5 Experiments

In this section,we conduct several experiments on some 2D natural images to evaluate the performance of HDM and the optimisation method.The natural images are shown in Fig.3.Those images all are 1024×1024 pixels.In order to illustrate the performance of the HDM,we compare HDM with the SpaRan matrix[5],the LDPC matrix[7],the BCH matrix[9],the Hadamard matrix[10],and the ToeCir matrix [8].Moreover,we compare the reconstruction results with different measurement matrices before and after optimisation to illustrate the performance of the optimisation method.There are two parameters(tγ,α)considered in the optimisation method.The tγis set to the mean of the singular values and theαis set to 6 based on the experiments.In our experiments,the image in the sparse domain is sampled by these measurement matrices and the OMP algorithm is set as the reconstruction algorithm.The reconstruction results of different measurement matrices are evaluated by the peak signal-to-noise ratio(PSNR)and the structural similarity index(SSIM).The value of the SSIM is always between[0,1].The greater the value of both the PSNR and the SSIM,the less the image distortion.All the experiments are performed on the personal computer with a 3.50 GHz Intel CPU and 4 GB of memory.The computer runs on windows 10,with MATLAB 2012b.

In the first experiment,we reconstruct Fig.3a Lena image versus the SpaRan matrix,the LDPC matrix,the BCH matrix,the Hadamard matrix,the ToeCir matrix,the HDM,and their optimised matrices.The sample rate is 20%.Figs.4-6 show the reconstructed images via different measurement matrices.Obviously,the HDM gets a better performance than the other measurement matrices both before and after the optimisation.In addition,all the measurement matrices perform better after optimised.Further,the PSNR of the reconstruction images via the HDM are the highest in every image under different sampling rates.Furthermore,Figs.7 and 8 show the outstanding performance of the optimisation strategy more vividly.

In the second experiment,we reconstruct all the four experimental images versus the SpaRan matrix,the LDPC matrix,the BCH matrix,the Hadamard matrix,the ToeCir matrix,and the HDM with different sampling rates.The different PSNRs of the reconstructed images(Boat,Baboon,Peppers)under different sampling rates are shown in Table 3.We can see the PSNR improved with the increasing in the sampling rate for all the matrices from Table 3.Further,the PSNR of the reconstruction images via the HDM are the highest in every image under different sampling rates.Furthermore,Figs.9 and 10 show the outstanding performance of the HDM more vividly.

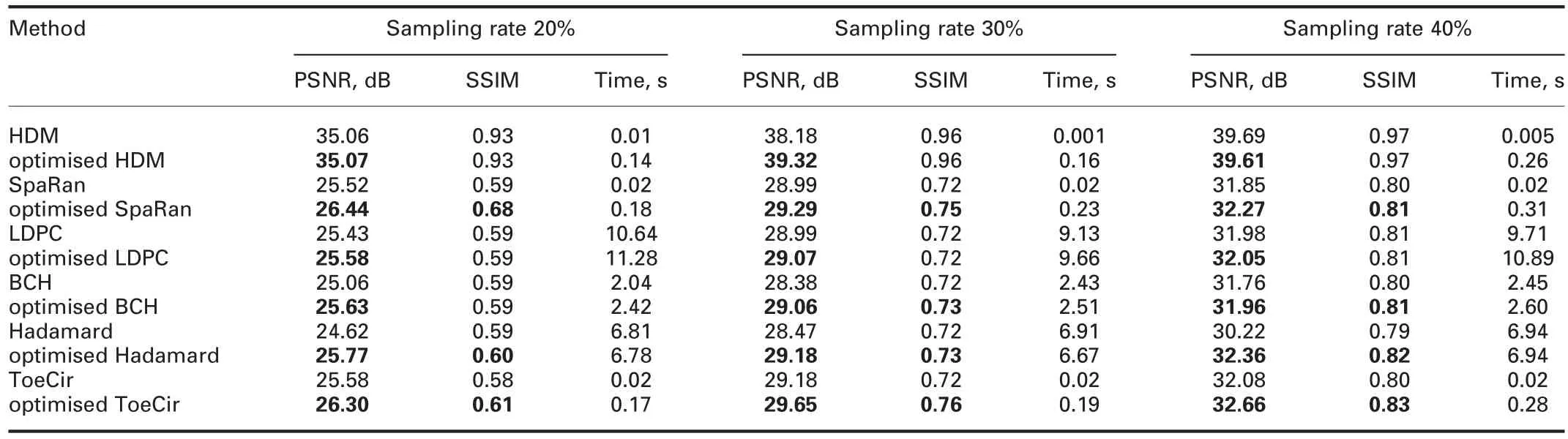
Table 5 PSNR,SSIM,and time of the reconstruction images with different measurement matrices in different sampling rates

In the third experiment,we reconstruct all the four natural images versus the SpaRan matrix,the LDPC matrix,the BCH matrix,the Hadamard matrix,the ToeCir matrix,and the HDM with different sparse basis(DCT,DWT).Table4shows PSNR of the reconstructed images where the sampling rate is 25%.Obviously,the HDM keeps a good performance with different sparse basis which means the HDM can keep incoherent with these sparse basis well.

In the fourth experiment,we reconstruct the experimental image Fig.1a with all the measurement matrix(the SpaRan matrix,the LDPC matrix,the BCH matrix,the Hadamard matrix,the ToeCir matrix,and the HDM)and whose optimised matrix with different sampling rates.From Tables 1 and 5,we can see the optimised HDM performs better than the HDM.In addition,the other optimised matrices also get better reconstruction results than the original measurement matrices.Which means the optimisation strategy hasa good general applicability.From the time comparison of the measurement matrices before and after the optimisation in Tables 1 and 5,we can find the increased time is very little.

6 Conclusion

In this paper,we propose a simple but efficient measurement matrix based on the Hadamard matrix for CS.With considering maximising the energy conservation of the natural images in the sparse domain,the main sensing rows and columns are fixed in the Hadamard matrix with ‘1’and the others with ‘0’to obtain more energy after the sampling in the sparse domain,which is helpful to improve the sensing efficiency even the accuracy of reconstruction.Hence,HDM is binary and sparse,which will help to be implemented in hardware.In addition,an effective optimisation algorithm is adopted,which further improves the quality of reconstruction.The experiment results show that HDM performs better than other existing measurement matrices and the optimisation algorithm is effective for not only the HDM but also the other popular measurement matrices.

7 Acknowledgments

This work was supported by the National Science Foundation of China(grant no.61673220 and grant no.61401220).

8 References

[1] Candès,E.J.: ‘Compressive sampling’.Proc.of the Int.Congress of Mathematicians,Madrid,Spain,2006,pp.1433-1452

[2] Donoho,D.L.: ‘Compressed sensing’,IEEE Trans.Inf.Theory,2006,52,(4),pp.1289-1306

[3] Candès,E.J.,Tao,T.:‘Near-optimal signal recovery from random projections:universal encoding strategies’,IEEE Trans.Inf.Theory,2006,52,(12),pp.5406-5425

[4] Zhang,G.,Jiao,S.,Xu,X.,et al.:‘Compressed sensing and reconstruction with Bernoulli matrices’.IEEE Int.Conf.on Information and Automation,Harbin,China,2010,pp.455-460

[5] Berinde,R.,Indyk,P.:‘Sparse recovery using sparse random matrices’.Preprint,2008

[6] Dimakis,A.G.,Vontobel,P.O.:‘LP decoding meets LP decoding:a connection between channel coding and compressed sensing’.47th Annual Allerton Conf.on Communication,Control,and Computing,Allerton,2009,pp.8-15

[7] Dimakis,A.G.,Smarandache,R.,Vontobel,P.O.:‘Ldpc codes for compressed sensing’,IEEE Trans.Inf.Theory,2012,58,(5),pp.3093-3114

[8] Yin,W.,Morgan,S.,Yang,J.,et al.:‘Practical compressive sensing with toeplitz and circulant matrices’.Proc.SPIE,Huangshan,China,2010,vol.7744,p.77440K

[9] Amini,A.,Marvasti,F.:‘Deterministic construction of binary,bipolar,and ternary compressed sensing matrices’,IEEE Trans.Inf.Theory,2011,57,(4),pp.2360-2370

[10] Gan,L.,Do,T.T.,Tran,T.D.:‘Fast compressive imaging using scrambled block hadamard ensemble’.16th European IEEE Signal Processing Conf.,Lausanne,Switzerland,2008,pp.1-5

[11] Candès,E.J.,Tao,T.: ‘Decoding by linear programming’,IEEE Trans.Inf.Theory,2005,51,(12),pp.4203-4215

[12] Donoho,D.L.,Huo,X.:‘Uncertainty principles and ideal atomic decomposition’,IEEE Trans.Inf.Theory,2001,47,(7),pp.2845-2862

[13] Donoho,D.L.,Elad,M.:‘Optimally sparse representation in general(non-orthogonal)dictionaries via ?1minimization’,Proc.Natl.Acad.Sci.USA,2003,100,(5),pp.2197-2202

[14] Baraniuk,R.G.: ‘Compressive sensing[lecture notes]’,IEEE Signal Process.Mag.,2007,24,(4),pp.118-121

[15] Elad,M.:‘Optimized projections for compressed sensing’,IEEE Trans.Signal Process.,2007,55,(12),pp.5695-5702

[16] Abolghasemi,V.,Sanei,S.,Ferdowsi,S.,et al.:‘Segmented compressive sensing’.IEEE/SP 15th Workshop on Statistical Signal Processing,Cardiff,UK,September 2009

[17] Wang,Z.,Arce,G.R.: ‘Variable density compressed image sampling’,IEEE Trans.Image Process.,2010,19,(1),pp.264-270

[18] Wang,Z.,Arce,G.R.,Paredes,J.L.:‘Colored random projections for compressed sensing’.IEEE Int.Conf.on Acoustics,Speech and Signal Processing,Honolulu,Hawaii,April 2007,pp.873-876

[19] Duarte-Carvajalino,J.,Sapiro,G.:‘Learning to sense sparse signals:simultaneous sensing matrix and sparsifying dictionary optimization’,IEEE Trans.Image Process.,2009,18,(7),pp.1395-1408

[20] Li,X.,Bai,H.,Hou,B.:‘A gradient-based approach to optimization of compressed sensing systems’,Signal Process.,2017,139,pp.49-61

[21] Cleju,N.:‘Optimized projections for compressed sensing via rank-constrained nearest correlation matrix’,Appl.Comput.Harmon.Anal.,2014,36,(3),pp.495-507

[22] Mallat,S.G.,Zhang,Z.: ‘Matching pursuits with time-frequency dictionaries’,IEEE Trans.Signal Process.,1993,41,(12),pp.3397-3415

[23] Tropp,J.A.,Gilbert,A.C.:‘Signal recovery from random measurements via orthogonal matching pursuit’,IEEE Trans.Inf.Theory,2007,53,(12),pp.4655-4666

[24] Needell,D.,Vershynin,R.:‘Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit’,Found.Comput.Math.,2009,9,(3),pp.317-334

[25] Needell,D.,Tropp,J.A.:‘Cosamp:iterative signal recovery from incomplete and inaccurate samples’,Appl.Comput.Harmon.Anal.,2009,26,(3),pp.301-321

[26] Do,T.T.,Gan,L.,Nguyen,N.,et al.:‘Sparsity adaptive matching pursuit algorithm for practical compressed sensing’.42nd Asilomar Conf.on Signals,Systems and Computers,Asilomar,2008,pp.581-587

[27] Gribonval,R.,Nielsen,M.: ‘Sparse representations in unions of bases’,IEEE Trans.Inf.Theory,2003,49,(12),pp.3320-3325

[28] Candès,E.J.,Wakin,M.B.: ‘An introduction to compressive sampling’,IEEE Signal Process.Mag.,2008,25,(2),pp.21-30