Cryptanalysis of Key Exchange Protocol Based on Tensor Ergodic Problem
Chunsheng Gu*, Youyu Gu, Peizhong Shi Chunpeng Ge Zhenjun Jing
1 School of Computer Engineering, Jiangsu University of Technology, Changzhou 213001, China
2 State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
3 School of Mathematics, Hefei University of Technology, Hefei 230000, China
Abstract: Recently, Mao, Zhang, Wu et al.constructed two key exchange (KE) protocols based on tensor ergodic problem (TEP). Although they conjectured that these constructions can potentially resist quantum computing attack, they did not provide a rigorous security proof for their KE protocols. In this paper,applying the properties of ergodic matrix, we first present a polynomial time algorithm to solve the TEP problem using O(n6) arithmetic operations in the finite field, where n is the security parameter. Then, applying this polynomial time algorithm, we generate a common shared key for two TEP-based KE constructions, respectively. In addition, we also provide a polynomial time algorithm with O(n6)arithmetic operations that directly recovers the plaintext from a ciphertext for the KE-based encryption scheme. Thus, the TEP-based KE protocols and their corresponding encryption schemes are insecure.
Keywords: key exchange; KE-based encryption; tensor decomposition; ergodic matrix
I. INTRODUCTION
Key exchange (KE) protocol is an important cryptographic primitive that enables two users to establish a common session key by communicating over a public channel. The first KE protocol is given by Diffie and Hellman [1],using the discrete logarithm problem. Similarly, the Diffie-Hellman KE can be directly extended to the discrete logarithm over elliptic curve. Moreover, a 3-party KE protocol is constructed by Joux [2] using pairings on elliptic curve. However, a quantum polynomial time algorithm proposed by Shor [3] solves the integer factorization problem and the discrete logarithm problem, including the discrete logarithm over elliptic curve. Therefore, all KE protocols currently used in practice will become insecure once sufficiently large quantum computers can be built.
Alternative KE protocols that potentially resist quantum computer attacks have been proposed. On the one hand, several lattice-based KE protocols [5-8] are constructed. Peikert[5] and Ding, Xiang and Lin [6] described the RLWE/LWE-based KE protocols, respectively.Wang, Zhu, Ma et al. [7] proposed a SIS-based KE protocol. On the other hand, some KE protocols based on new hardness assumptions are given by [8-10]. Garg, Gentry and Halevi [8]described a multipartite Diffie-Hellman key exchange protocol based on their multilinear map. Unfortunately, this KE protocol has been broken by Hu and Jia [11]. Since most tensor matrix problems are NP-hard [12-14], this motivated that Mao, Zhang, Wu et al. [9-10]constructed the KE protocols based on these new hardness problems. However, they did not provide a rigorous security proof for their KE protocols, even if they conjectured that these constructions can potentially resist quantum computing attack. Thus, it is necessary to analyze the security of these schemes.
Our main contribution is to prove that the KE protocols [9-10] based on tensor ergodic problem (TEP) are insecure. To construct key exchange protocol, Mao, Zhang, Wu et al.[9-10] first introduced TEP by using tensor decomposition problem and ergodic matrix as basic building blocks. Then they constructed two TEP-based KE protocols. Although most tensor problems [12-13] are NP-hard, this does not mean that the TEP problem is also computationally hard. In fact, there exists a polynomial time algorithm for the TEP problem. Using this polynomial time algorithm,we can generate a common shared key of the TEP-based KE protocols in [9-10], respectively. Thus, this paper breaks the TEP-based KE protocols in [9-10]. Furthermore, this paper also breaks the KE-based encryption scheme in [10].
The remainder of this paper is organized as follows.We first describe preliminaries about TEP in Section 2, and give a polynomial time algorithm for TEP in Section 3. Then, we break two TEP-based KE schemes in Section 4 and Section 5, respectively. Next, we break a KE-based encryption scheme in Section 6.Finally, we conclude this paper and give some suggestions for possible improvements.
II. PRELIMINARIES
For better description, we first define some basic notations in this paper. Let ? be the set of natural numbers, ? the ring of integers. Let m,n∈?, and set [n]={1,2,…,n}. Given a prime q, let ?q=?/q? denote a finite field,the set of n-dimensional column vectors over ?q,the set of m×n-dimensional matrices over ?q. By convention, vectors are in column form and are denoted by lower-case bold letters (e.g.x), matrices by capital bold letters (e.g.A). Notation ? denotes tensor product over ?q.
Let n be the security parameter. Throughout this paper, all computations operate over the finite field ?q, unless otherwise stated.For simplicity, we consider the time for one arithmetic operation over ?qas “1” unit, and omit modulus q in the following formula.
In the following, we adaptively give the definitions about tensor of matrix, ergodic matrix, and tensor ergodic problem in [9-10].
Definition 1 (Tensor of Matrix).Given two matrices A∈,B ∈, define the tensor product A?B as an mk×nl-dimensional matrix as follows:

where A=(ai,j),i∈[m],j∈[n].
Definition 2 (TDP: Tensor Decomposition Problem).Given A=A1?A2?A3,find matrices,i∈[3] such that, where, i∈[3]are random matrices.
Definition 3 (EM: Ergodic Matrix).Given a matrix Q∈and any nonzero vector x∈, if {Qx,Q2x,…,Qqn?1x} run through{0}, then Q is called an ergodic matrix over ?q.
Definition 4 (EMP: Ergodic MatrixProblem).Givenfind s(Q1),t(Q2) such that
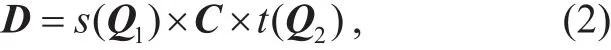
where Q1,Q2∈are ergodic matrices,C∈{0}, and s,t∈[[qn?1]].
Definition 5 (TEP: Tensor-Ergodic Problem).Given {Q1,Q2,C,C1} with, find X', Y', s(Q1),t(Q2) such that
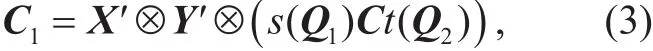
where Q1,Q2∈are ergodic matrices,C∈{0},X∈,Y ∈, and
Note that EMP and TEP are defined as computing matrices s(Q1),t(Q2) in this paper,whereas they are defined as computing exponents s,t∈[[qn?1]] in [9-10].
III. POLYNOMIAL TIME ALGORITHM FOR TEP
Although authors in [9-10] conjectured that TEP is computationally hard and constructed a TEP-based one-way function, they did not provide a rigorous proof about the hardness of TEP. In this section, we present a polynomial time algorithm which solves TEP. In the following, we first give several related lemmas about TEP.
Lemma 1 (Properties of tensor product,[9]).Suppose,i∈[4]. Then, we have
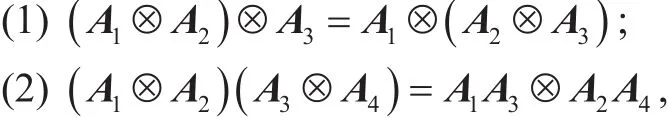
when n1=m3and n2=m4.
Proof. By the definition of tensor product,the result directly follows.
Lemma 2.Given an arbitrary element r∈and,j∈[3], then
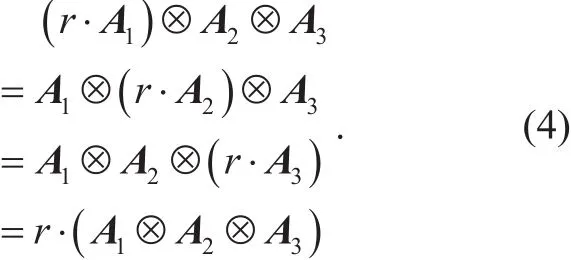
Proof. By the definition of tensor of matrix,we have
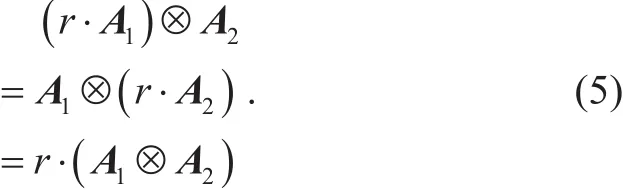
Repeating the above method, we can obtain the result.
Lemma 3.Given an arbitrary element r∈and,j∈[k], then
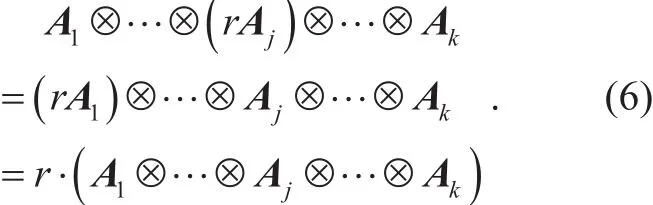
Proof. Using induction and Lemma 2, the result follows.
Lemma 4. Suppose that Q∈is an ergodic matrix. Then the determinant
Proof. By contradiction, assume
On the one hand, there exists an invertible matrixsuch that
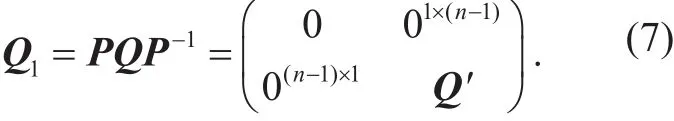
On the other hand, given Q, then for any nonzero vector x∈,
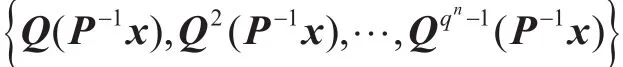
This generates a contradiction.
Lemma 5. Suppose that Q∈is an ergodic matrix. Thenand Qqn?1=I .
Proof. On the one hand, given Q, we have Qi≠Q(mào)jif i,j∈[[qn?1]] and i≠j. Otherwise, there exist i,j∈[[qn?1]] and i>j such that Qi=Qj, then Qi?j=I anddo not run through
On the other hand, the characteristic polynomialis a monic n-degree polynomial and f(Q)=0, so. Again by, we getand
Lemma 6. Suppose thatis the characteristic polynomial of ergodic matrix Q. Then f(λ) is an n-degree irreducible minimal polynomial of Q over ?q[λ].
Proof. By contradiction, assume f(λ)=a(λ)b(λ) such that the degrees of a(λ),b(λ) are less than n.
Since f(Q)=0, we have a(Q)b(Q)=0.
By Lemma 4, every element inQ is an invertible matrix. Since?q[Q]{0}=Q, so every matrix in ?q[Q]{0} is invertible.
Again, by a(Q),b(Q)∈?q[Q] and a(Q)b(Q)=0, hence a(Q)=0 or b(Q)=0. Without loss of generality, we assume a(Q)=0. Since the elements in ?q[Q] are one-to-one corresponding to elements in?q[λ]/a(λ), thus. As a consequence,. This contradicts that Q is an ergodic matrix.
This competes the proof of Lemma 6.
Lemma 7.Suppose that Q is an ergodic matrix. Then S={Q0=I,Q1,…,Qn?1} is a basis of ?q[Q].
So this wonderful, warm woman laid the palm of her golden brown hand on my pale chest and she gently held it there. For a long time. I continued to cry quietly. In soft tones she said, This is part of your body. This is you. It s okay to touch it. But I couldn t. So she touched it for me. The scar. The healing wound. And beneath it, she touched my heart.Then Ramona said, I ll hold your hand while you touch it. So she placed her hand next to mine, and we both were quiet. That was the gift that Ramona gave me.
Proof.By Lemma 6,is an n-degree irreducible minimal polynomial.So, any element in ?q[λ]/f(λ) is corresponding to polynomial r(λ) with degree less than n, namelySince Qkis one-to-one corresponding to r(λ)=λkmodf (λ), we get Qk=r(Q ).Moreover, the degrees of Q in r(Q) are less than n, thus any element in ?q[Q] can be generated by S. Similarly, every element generated by S belongs to ?q[Q].
Again, by the irreducibility of f(λ), f(Q)is a minimal polynomial in the variable Q such that g(Q)=0. Hence, the elements in S are linear independent.
Lemma 8.Suppose that Q is an ergodic matrix. Then ?q[Q] satisfies multiplicative commutative law.
Proof.Let a(Q),b(Q)∈?q[Q ] be two arbitrary elements in ?q[Q]. By Lemma 7,. Then,we have
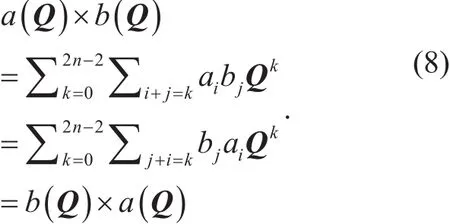
So, the result follows.
Lemma 9. Suppose that Q is an ergodic matrix. Given D'=r·Qswith a nonzero element r∈?q, then there exists an integersuch that D'=Qs'.
Proof.By Lemma 5, we obtain Qs∈Q=?q[Q]. For r∈?q{0}, hence. Again sincethere exists an integersuch that
Lemma 10.Suppose Q1,Q2are ergodic matrices. Given C,D such thatthen there exists a polynomial time algorithm which finds matrices s(Q1), t(Q2) such that
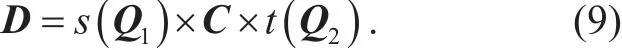
Proof.By Lemma 6,i∈?2? are the irreducible polynomial with degree n. Using Lemma 7 and fi(Qi)=0,i∈[2], we have
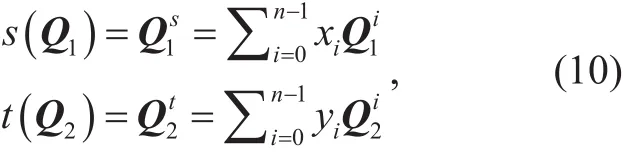
In the following proof, we first provide Algorithm 1 to solve s(Q1), t(Q2). Then,we show that Algorithm 1 runs in polynomial time.
Algorithm 1: Solving s(Q1), t(Q2).
Input: Q1, Q2, C,D.
Output: s(Q1), t(Q2).
(1) Generate a quadratic system of equations
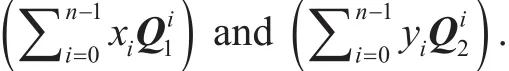
(1.3) Generate a matrix equation and arrange into a quadratic system of n2equations with 2n unknown variables x,y:
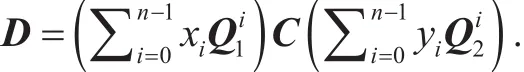
(2) Linearize the quadratic system
(2.1) Let zi,j=xiyj,i,j∈{0,1,…,n ?1} be unknown variables.
(2.2) Transform the quadratic system into a linear system of equations with n2variables.We denote by Az=b this linear system of equations.
(3) Solve the linear systemAz=b
Using Gaussian elimination method, solve Az=b to obtain
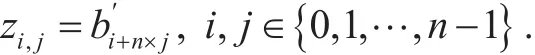
(4) Solve2nunknown variablesx,y
(4.1) Find zi0,j0=xi0yj0=with, and set
(4.3) By zi0,j=xi0yj=b, set
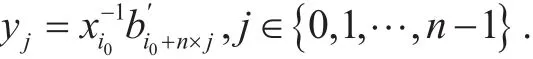
(5) Compute and returns(Q1), t(Q2)
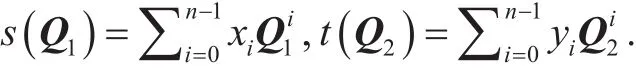
Note that yj0above can be set any nonzero value. Hence, we can find p?1 solutions such that D=s(Q1)×C×t (Q2), where
Here s(Q1), t(Q2) may not be the same as,, however D=s(Q1)×C×t (Q2) must hold.
Time and space analysis of Algorithm 1.
Note that the time for one arithmetic operation over ?qis considered as “1” unit in this paper.
Step (1)costs time O(n5).
(1.3) Generating each element ofrequires time O(n3). Consequently, generatingtakes time n2×O(n3)=O(n5).
Step (2)takes time n2×O(n2)=O(n4).
Step (3)Gaussian elimination method costs time O((n2)3)=O(n6). This is because A is an n2×n2-dimensional matrix.
Step (4)costs time O(n2).
Step (5)costs time O(n3).
In addition, it is easy to verify that Algorithm 1 requires space about O(n4).
Thus, Algorithm 1 using O(n6) arithmetic operations can find s(Q1), t(Q2) such that D=s(Q1)×C×t (Q2).
Theorem 11. Given {Q1,Q2,C,C1} with, then there exists a polynomial time algorithm which solves X',Y', s'(Q1),t'(Q2) such that
Proof.Given, we can obtainby Lemma 2. Without loss of generality, we let r=x1,1y1,1∈?q{0} and for notational simplicity write D'=Di1,j2,i2,j2. Otherwise, we may choose other subscripts. Similarly, we get
Again, by Lemma 2, we have
The proof is complete.
Similarly, we have the following result.
Corollary 12. Given {Q1,Q2,C,C1} with, then there exists a polynomial time algorithm, which computes
Proof.The proof is same as that of Theorem 11.
IV. CRYPTANALYSIS OF KE1
In this section, we first adaptively give the key exchange protocol based on TEP (KE1) in [9].Then, we present a polynomial time algorithm which generates a common shared key. As a result, we break the KE1 construction.
4.1 Construction of KE1
Setup.
Given parameters n,q, choose two ergodic matrices Q1,Q2∈, and a random matrix C∈. Output the public parameters pp={n,q,Q1,Q2,C}.
Publish.
Alice sends K1to Bob, and remains s1,t1,X1,Y1secret.
(2) Bob randomly selects s2,t2∈[[qn?1]]and X2,Y2∈, and computes
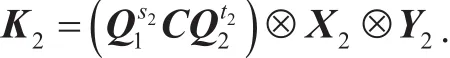
Bob sends K2to Alice, and remains s2,t2,X2,Y2secret.
KeyGen.
Let Ii,i∈[4] be n2×n2identity matrices.
(1) Alice generates the common shared key
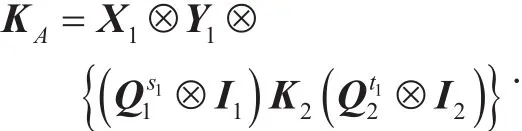
(2) Bob generates the common shared key
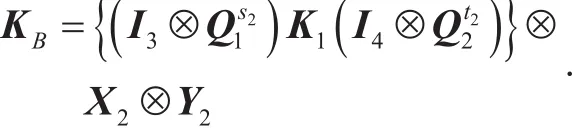
It is easy to verify that KA,KBare equal to
4.2 Cryptanalysis of KE1
To break KE1, we only require to generate a common shared key by using the public parameters and matrices sent by both parties in the process of executing KE1.
Theorem 13. Given the public parameters pp, K1, K2, then there exists a polynomial time algorithm which generates a common shared key
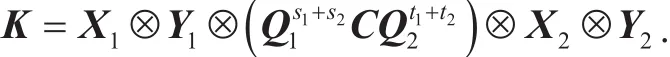
Proof.Given pp,K1,K2, we generate
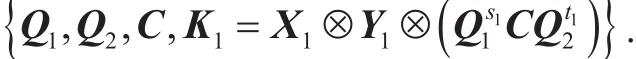
For simplicity, we write
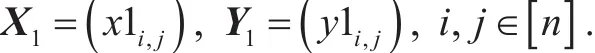
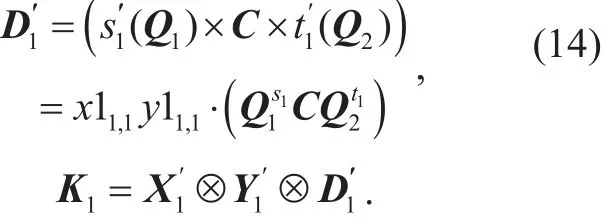
Let Ii,i∈[2] be the n2×n2identity matrices. We generate a common shared key K as follows:
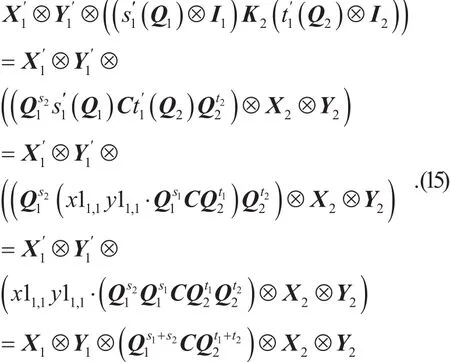
Note that the first equation uses the multiplicative commutativity law for the ergodic matrices in Lemma 8.
It is not difficult to verify that the above algorithm runs in polynomial time.
The proof is complete.
V. CRYPTANALYSIS OF KE2
Similar to the cryptanalysis of KE1 in Section 4, we first adaptively give the key exchange protocol based on TEP (KE2) in [10]. Then,we present a polynomial time algorithm,which generates a common shared key. Consequently, we break the KE2 construction.
5.1 Construction of KE2
Setup.
Given parameters n,q, choose two ergodic matrices, a random matrix, and dimensions m1, m2, n1, n2, k, l such that m1≠n1,m1≠k , m2≠n2, l≠n2.
Output the public parameters
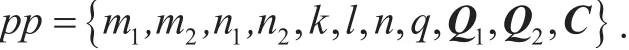
Publish.
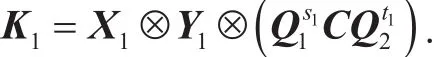
Alice sends K1to Bob, and remains{X1,Y1,s1,t1} secret.
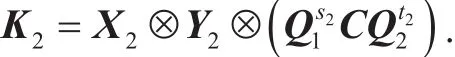
Bob sends K2to Alice, and remains{X2,Y2,s2,t2} secret.
KeyGen.
Let I1be the l×l identity matrix, I2be the k×k identity matrix, I3be the m1×m1identity matrix, I4be the n2×n2identity matrix.
(1) Alice generates the common shared key
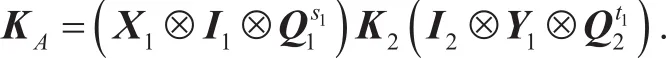
(2) Bob generates the common shared key
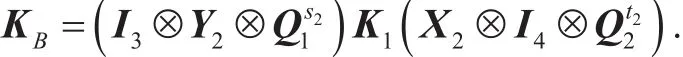
It is easy to verify that KA,KBare equal to
5.2 Cryptanalysis of KE2
To break KE2, we only require to compute a common shared key by using the public parameters and matrices sent by both parties in the process of executing KE2.
Theorem 14. Given the public parameters pp, K1, K2, then there exists a polynomial time algorithm which generates a common shared key
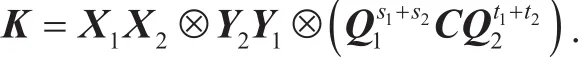
Proof.Given pp,K1,K2, we generate
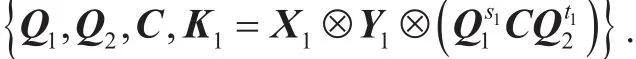
For simplicity, we write
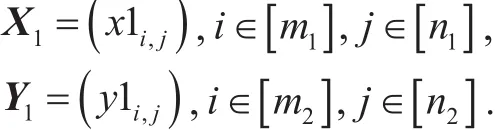
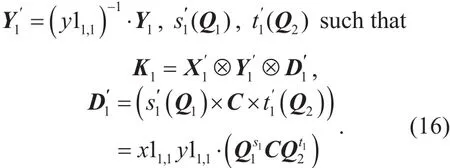
Let I1be the l×l identity matrix, I2be the k×k identity matrix. We generate a common shared key K as follows:
It is easy to verify that the above algorithm runs in polynomial time.
The proof is complete.
VI. CRYPTANALYSIS OF KE2-BASED ENCRYPTION
Mao, Zhang, Wu et al. also constructed a KE2-based encryption scheme in [10] that uses KE2 as a basic building block. Consequently, we can break this encryption scheme by applying same method in Section 5. In the following, we first give the KE2-based encryption scheme. Then, we propose a polynomial time algorithm, which directly recovers the plaintext from the ciphertext and the public key.
6.1 KE2-based encryption scheme
Setup.
Given parameters n, q, choose two ergodic matrices, a random matrix, and dimensions m1,m2, n1,n2, k, l such that m1≠n1, m1≠k , m2≠n2,l≠n2. Output the public parameters
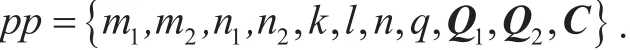
Let I1be the l×l identity matrix, I2be the k×k identity matrix, I3be the m1×m1identity matrix, I4be the n2×n2identity matrix.
KeyGen.
(3) Output the public key pk={P}, and the private key sk={X1,Y1,s1,t1}.
Encryption.
Let d1=m1×n× l and d2=n×n2×k . Let m={0,1}d1be a plaintext vector.
(2) Compute C1, c2as follows:
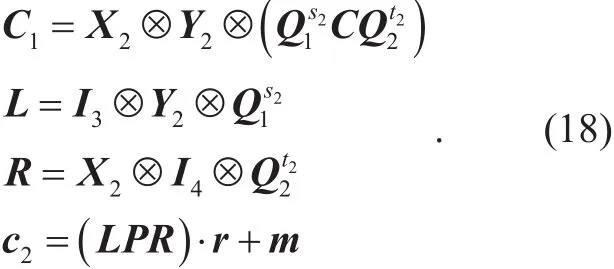
(3) Output a ciphertext ct={C1,c2,r}.
Decryption.
Given the private key sk and the ciphertext ct={C1,c2,r}:
(1) Compute K as follows:
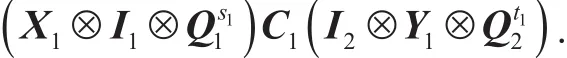
(2) Decrypt the plaintext m=c2?K×r.
6.2 Cryptanalysis of KE2-based encryption scheme
Given the public key and a ciphertext, we can directly recover the corresponding plaintext from the ciphertext. As a result, we break the KE2-based encryption scheme.
Theorem 15. Given the public parameters pp, the public key pk, and a triple ciphertext ct={C1,c2,r }, then there exists a polynomial time algorithm which recovers the plaintext m in the ciphertext ct.
Proof.Given pp, pk, ct, we generate
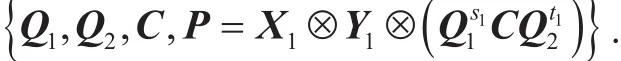
We denote
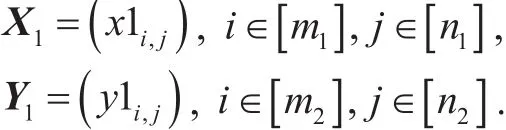
By Theorem 11, we can computesuch that
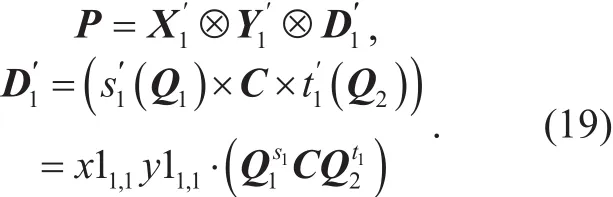
Then, we compute K as follows:
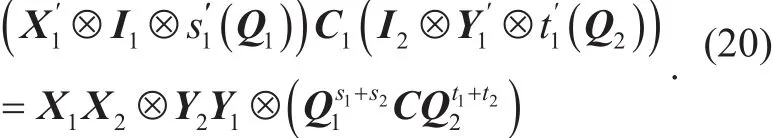
Finally, by using K, we decrypt the ciphertext ct to get the plaintext m=c2?K×r .
Similarly, the above algorithm runs in polynomial time.
The proof is complete.
VII. CONCLUSIONS
In this paper, we first present a polynomial time algorithm for the TEP problem. Then,using this polynomial time algorithm, we generate a common shared key for the TEP-based KE constructions described by Mao, Zhang,Wu et al. [9-10], respectively. In addition, we also provide a polynomial time algorithm,which directly recovers the plaintext from a ciphertext for the KE2-based encryption scheme. Thus, the TEP-based KE protocols and their corresponding encryption schemes in[9-10] are insecure.
To obtain a secure TEP-based KE, further improvements are necessary. According to our cryptanalysis in this paper, any improvement of the TEP-based KE is preferably capable of providing a rigorous security proof. A possible direction is to introduce some noise elements in the TEP-based KE construction. Currently,it remains an open problem how to construct a secure post-quantum TEP-based KE.
ACKNOWLEDGMENTS
This paper was supported by the National Natural Science Foundation of China (No.61672270, 61602216, 61702236), the Qing Lan Project for Young Researchers of Jiangsu Province of China (No. KYQ14004), and the Open Fund of State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences (No.2015-MSB-10), Jiangsu Overseas Research& Training Program for University Prominent Young & Middle-aged Teachers and Presidents, Changzhou Sci&Tech Program, (Grant No.CJ20179027).
- China Communications的其它文章
- A Precise Information Extraction Algorithm for Lane Lines
- Energy-Efficient Multi-UAV Coverage Deployment in UAV Networks: A Game-Theoretic Framework
- An Efficient Algorithm for Skyline Queries in Cloud Computing Environments
- Physical-Layer Encryption in Massive MIMO Systems with Spatial Modulation
- A Robust Energy Efficiency Power Allocation Algorithm in Cognitive Radio Networks
- SVC Video Transmission Optimization Algorithm in Software Defined Network

