Physical-Layer Encryption in Massive MIMO Systems with Spatial Modulation
Sixin Wang, Wei Li*, Jing Lei
School of Electronic Science, National University of Defense Technology, Changsha 410073, China
Abstract: Massive multiple input and multiple output (MIMO) is a key technology of the fifth generation (5G) wireless communication systems, which brings various advantages, such as high spectral efficiency and energy efficiency.In MIMO system, spatial modulation (SM)has recently emerged as a new transmission method. In this paper, in order to improve the security in SM-MIMO, a physical layer encryption approach named chaotic antenna-index three-dimensional modulation and constellation points rotated (CATMCPR) encryption scheme is proposed, which utilizes the chaotic theory and spatial modulation techniques. The conventional physical-layer encryption in SM-MIMO suffers from spectral efficiency (SE) performance degradation and usually needs a preshared key, prior channel state information(CSI) or excess jamming power. By contrast,we show that the CATMCPR scheme can not only achieve securely communication but also improve above drawbacks. We evaluate the performances of the proposed scheme by an analysis and computer simulations.
Keywords: massive MIMO; chaotic system;physical layer security; antenna-index; spatial modulation
I. INTRODUCTION
Recent years, with the rapid development of 5G wireless communication system, massive MIMO has become a key technology [1],which can achieve high reliability, spectral efficiency and energy efficiency compared with traditional MIMO by exploiting plenty of excess service antennas at the base station (BS)[2]-[5]. However, the dramatically increasing data amount and complex communication environment put forward higher requirements on the security of mobile communications.
Conventional security communication scheme relies on the key-based cryptographic techniques at the upper layers, whereas the physical layer is designed to only guarantee the efficiency and reliability of communication through modulation and coding methods.Wireless physical layer security exploits the physical characteristic of the wireless channel to achieve secure communications, such as randomness, difference, reciprocity and so on.
Current development of wireless physical layer security technology has two main directions: one is to generate, manage and distribute keys based on the physical characteristics of the wireless channel, the other is based on the secrecy capacity and wiretap channel model proposed by Wyner on basis of Shannon’s information theory. Specifically, they can be divided into the following aspects: first,the corresponding security coding strategy is proposed according to the analysis of various types of wiretap channel model and secrecy capacity performance in different wireless channels based on information theory [6]; second, beamforming, artificial noise (AN) and
In this paper, we proposed a novel physical layer encryption scheme called CATMCPR to defend against eavesdroppers equipped with massive antennas and improve the energy efficiency in massive MIMO by using chaotic antenna-index and 3-D modulation.cooperative jamming are used in physical layer security schemes [7]; third, spatial diversity techniques can improve physical layer security, which takes advantage of multi-antenna diversity, multi-user diversity and cooperative diversity [8]; fourth, the key generated by the wireless channel characteristics can used to encrypt the message [9].
However, only a few of existing physical layer security schemes can be used in MIMO systems. In [10], the spatial signatures of MIMO channels are used to securely communicate in the presence of an eavesdropper.However, in order to ensure that decoding MIMO is hard for the eavesdropper, it requires a minimum noise level, which cannot be guaranteed usually. In [11], beamforming is used in massive MIMO to achieve physical layer security. Note that the transmitter has to know prior knowledge of the receiver channel. In addition, some physical layer security schemes,such as AN scheme [12], need to consume additional energy for sending artificial noise, at the cost of decreasing energy efficiency.
In this paper, we propose a physical layer encryption scheme in massive MIMO systems with SM, which has recently emerged as a new transmission method in MIMO system.Conventional massive MIMO systems usually map information bits to fixed constellation points in two-dimensional (2-D) complex plane, and it is limited to further enhance the transmission performance in 2-D modulation.Thus, more dimensions are considered to achieve better transmission performance.
Several works about multi-dimensional modulation have been done before. Y. Chau et.al [13] proposed Space Shift Keying (SSK),which uses the channel gain between different transmitting antennas to realize transmission of information. In [14], R. Mesleh et.al proposed a multi-antenna transmission scheme named spatial modulation. Renzo et.al [15]gave a specific application scenario to improve the capacity of spatial modulation. In [16] and[17], the authors propose a jointly mapped spatial modulation (JM-SM) scheme to break through the constraint on the number of transmit antennas in traditional SM systems. Compared with the traditional 2-D modulation, SM regards the antennas index as a new dimension. The key of SM is to divide the information bits into two parts artificially, wherein a portion is modulated by signals and the other portion is showed by different antennas. The classical SM scheme ensures that only one transmit antenna is working in a transmitting symbol slot. Therefore, a SM system, whose number of transmit antennas is N and modulation order is M, can send log2(MN) information bits. Then a series of studies have been conducted on the antenna array and random subcarrier weighting [18]. The main advantage of SM is that only one antenna is active at any time, which can eliminate the inter channel interference (ICI) in massive MIMO. In addition, using passive antennas to transmit information can make the communication system obtain higher energy efficiency. SM-MIMO takes advantage of the whole antenna array at the transmitter, while using a limited number of RF chains. The main distinguishing feature of SM-MIMO is that they map additional information bits onto an “SM constellation diagram” where each constellation element is constituted by either one or a subset of antenna elements.
The SM scheme also can be used to achieve security. SM-MIMO has demonstrated better secrecy capacity than that of its single antenna counterpart in the analysis of [19]. To further strengthen the secrecy rate of SM-MIMO, the authors of [20] proposed a transmit precoding method. However, this proposed transmit precoding method assumes knowledge of channel information from source-to-eavesdropper(or Alice to Eve), which lacks practicality for passive eavesdroppers. In [21] and [22],the authors studied the use of AN to degrade eavesdroppers’ signal reception, which needs to consume additional energy for sending AN and the transmitter must have prior knowledge of the receiver channel. Note that all of the SM-MIMO mentioned above have the fixed“spatial-constellation diagram”, which is not secure, and only a single transmitter antenna(TA) is active in every channel use no matter how many TAs there are, which leads to much lower spectral efficiency (SE).
In order to improve the security, we can disturb the “spatial-constellation diagram” using a random key, then the eavesdropper cannot decode the SM information. And in order to improve the spectral efficiency, we can make full use of TAs. In this paper, by combining chaotic theory with secret keys extraction technique based on wireless channel, secret keys generation algorithm is designed. Then,the keys are designed to protect the information bits, antenna combination and mapping modes (ACMM), and the CATMCPR scheme is proposed. Furthermore, we test the randomness of the keys we designed and analyze the secrecy, reliability and energy efficiency performance of the proposed scheme.
The main contributions of the paper are as follows:
? We propose a novel CATMCPR scheme for massive MIMO with SM. This scheme uses the antenna-index generated by chaotic sequence to protect the “spatial-constellation diagram”, which can achieve the physical layer security without a pre-shared secret key or prior CSI at the cost of little computational overhead.
? In addition, it can improve the SE compared with conventional SM-MIMO physical-layer security schemes, with the guarantee of high reliability and EE.
? Combining the technique of secret keys extraction based on wireless channel with the chaotic theory, an algorithm for secret keys generation is proposed.
? We conduct simulations and give a detailed analysis of security, reliability and efficiency to illustrate the merits of the CATMCPR scheme.
The rest of the paper is organized as follows.In Section II we outline the massive MIMO system model and describe the main idea of CATMCPR scheme. Section III introduces the CATMCPR scheme in detail. The simulation results and their analysis are given in Section IV. Finally, Section V concludes the paper.
II. SYSTEM MODEL
As shown in figure 1, a transmitter and legitimate receiver communicate with each other in the presence of a passive eavesdropper, labeled as Alice, Bob and Eve respectively. In this model, the number of antennas at Alice, Bob and Eve is denoted by NT, NRand Nerespectively. Both Bob and Eve have massive MIMO antenna arrays while the latter is far more powerful. So we have Ne?NT>0 and NT=NR,where NTand NRare finite, Neis infinite.
In the system model, the antenna-index,which is denoted by Book, stores various ACMMs. And the 3-D modulation is realized by SM scheme on the information bits. For security, the CATMCPR scheme adopts a three-level-encryption, corresponding to keys K1, K2and K3, which are generated here using chaotic sequences. The purpose of the first encryption level is to choose a ACMM from Book by K1. The second level scrambles the corresponding relationship between ACMM and memory addresses in Book by K2. At the last level, the constellation mapping is distributed with K3, which is a set of angles distributed in [0,2π] randomly, to protect the modulation type. Bob can decrypt the information by taking the reverse of the above operations in the appropriate order.
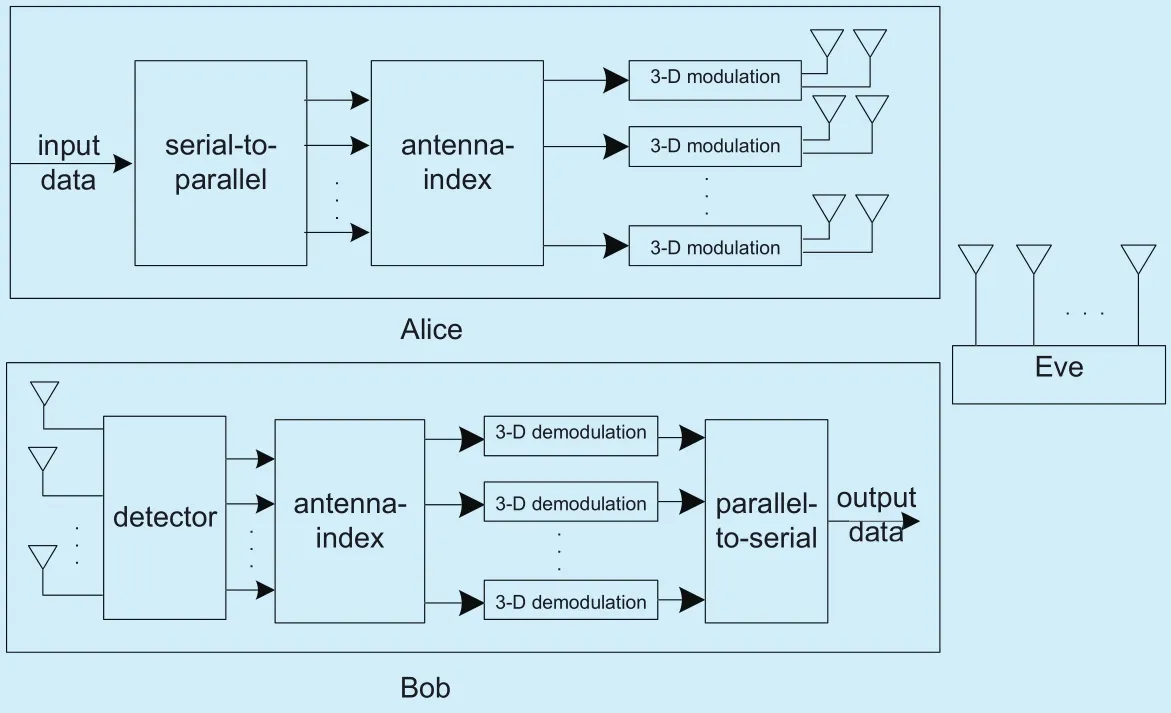
Fig. 1. Massive MIMO system model.
III. CHAOTIC ANTENNA-INDEX THREE-DIMENSIONAL MODULATION ENCRYPTION SCHEME
As is depicted in figure 2, the CATMCPR scheme can be separated into four steps, which will be introduced in Section 3.1.
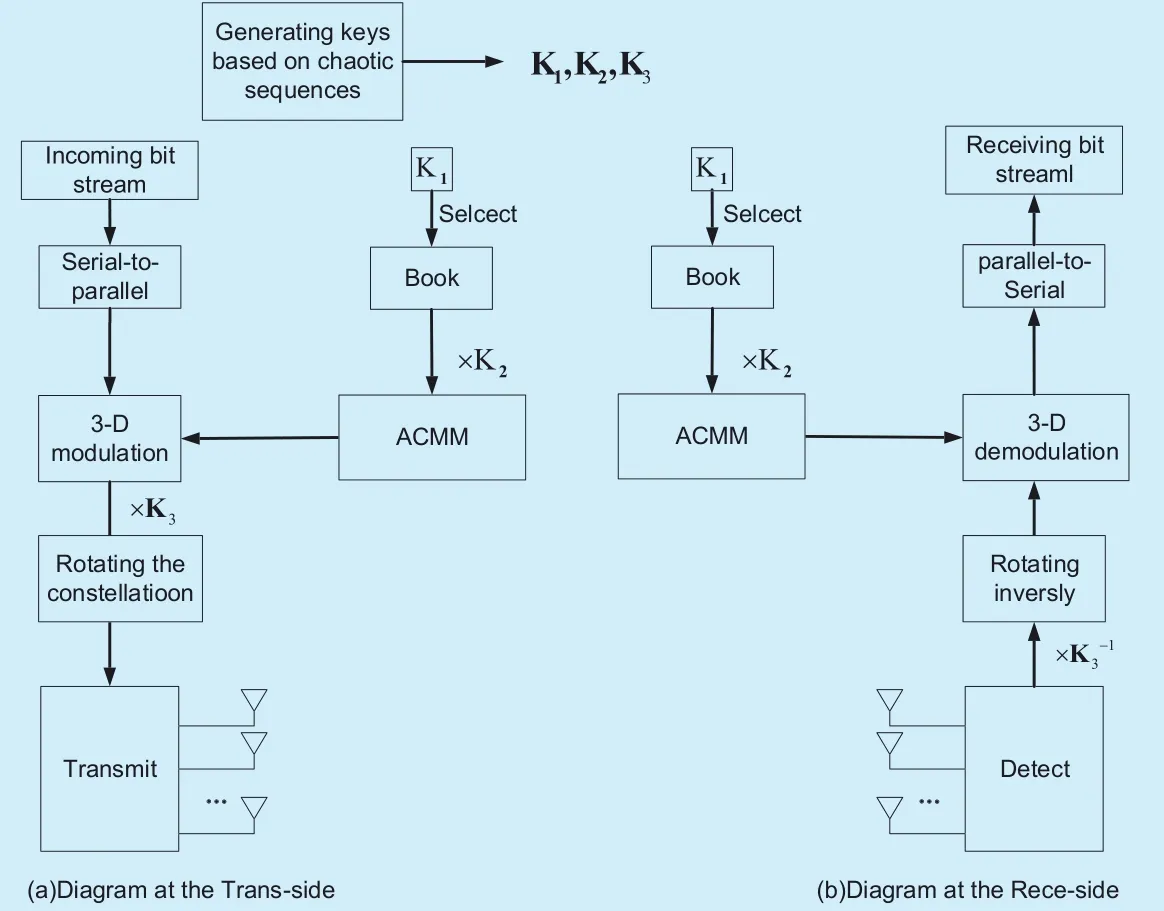
Fig. 2. The flowchart of CATMCPR scheme.
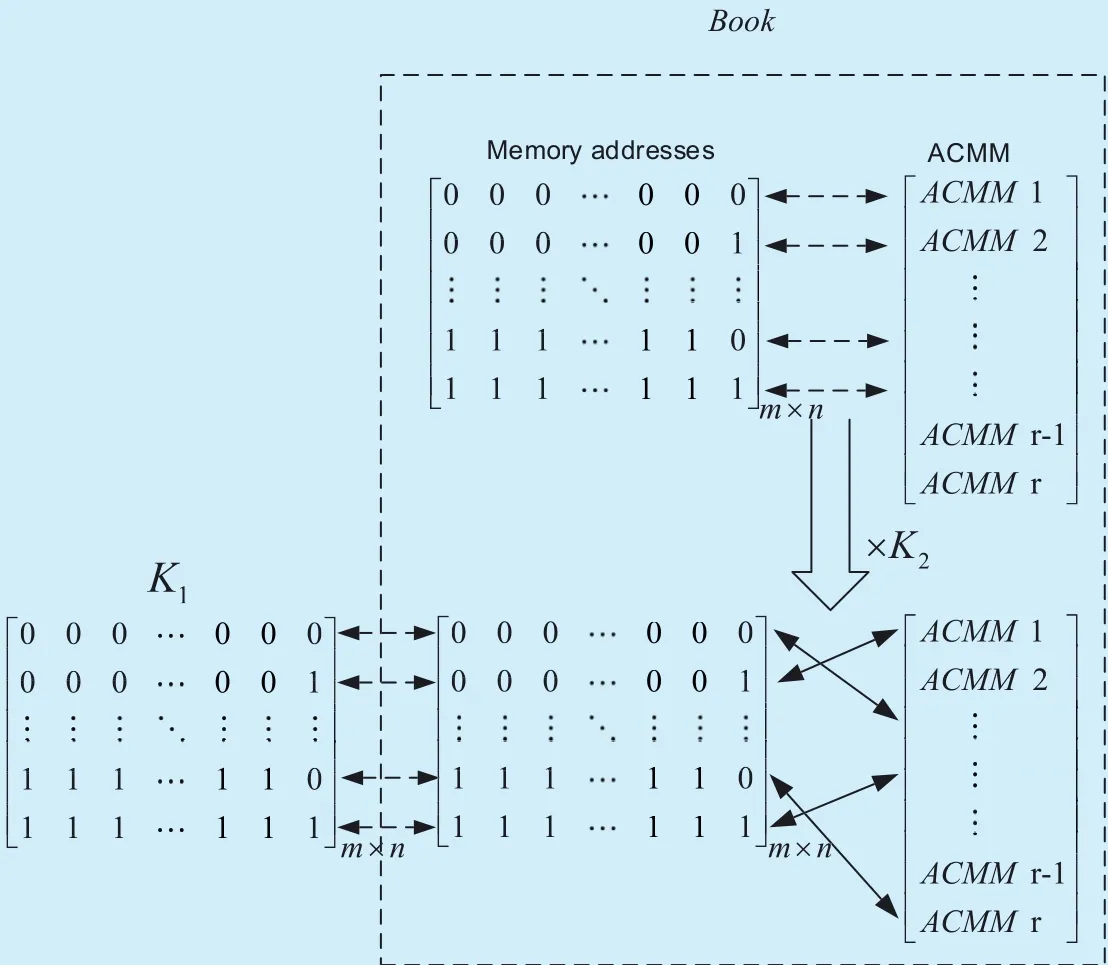
Fig. 3. Relationship among K1, memory addresses and ACMM in Book.
3.1 Detailed algorithm
Step 1. Generate the keys K1, K2and K3by the algorithm which will be introduced in SectionIII(B). The keys K1, K2and K3are used to choose an ACMM from Book, scramble the corresponding relationship between ACMM and memory addresses in Book, and rotate constellation points respectively.
Step 2. Establish the corresponding relationship between ACMM and memory address in Book. Different memory address stores different ACMM. The number of different antenna combination in Book isand the number of different mapping modes on every two antennas is (2M)!, where M is the modulation order and N is the number of transmitting antennas. Note that N should be even. Hence,Book consists of (N?1)!!×(2M)! ACMMs,which are stored in (N?1)!!×(2M)! memory addresses respectively. Then, K2is used to scramble the corresponding relationship between ACMM and the memory addresses, which can prevent Eve from intercepting right ACMM. Specifically, we make K1consist of the binary sequence whose length isat most. Then, the ACMM in the memory address that is equal to K1is chosen. Due to the scrambling step of K2, the key-space is up to (N?1)!!×(2M)!,which further improves the security of system. The relationship among K1, memory addresses and ACMM in Book is illustrated in figure 3, where m=2log2((N?1)!!×(2M)!)],and r=(N?1)!!×(2M)!. Note that in real massive MIMO system, we just store some of the whole ACMMs in Book and use them for encryption. However, for Eve, they don’t know which part of key space is used by Alice.Thus, Eve needs to try the whole key space,which is (N?1)!!×(2M)!.
Step 3. According to Step 2, an ACMM is chosen from Book by K1. Then, we map the bit stream after serial-parallel conversion to the activated antennas based on the selected ACMM, which is a 3-D modulation. The proposed CATMCPR scheme utilizes SM scheme to perform 3-D modulation on the information bits. For instance, the 3-D modulation constellation of Quadrature Phase Shift Keying (QPSK) is shown in figure 4, which is equipped with two transmitting antennas. The information bits are divided into a set of 3 bits group and every 3 bits are mapped to one symbol. Fig. 4 give an example of constellation mapping scheme, in which the first bit is used to select a transmission antenna, and the other two bits are used to determine the location of the constellation points on the selected antenna.
The comparison of the CATMCPR scheme with the traditional massive MIMO is shown in figure 4. In the traditional massive MIMO,illustrated in figure 5(a), a fixed number of information bits are mapped to constellation points in the 2-D signal domain through conventional modulation techniques, thus making the interception of the modulation type an easy task. Unlike the traditional massive MIMO system, as is depicted in the figure 5(b), the proposed CATMCPR scheme uses half of the transmitting antennas chosen by the antenna-index based on the chaotic theory to perform 3-D modulation. Due to the fact that only half of the transmitting antennas are activated, some energy is saved. ACMM divides transmitting antennas into N/2 groups and every group has 2 antennas, where N is the number of all transmitting antennas. Furthermore, ACMM decides the constellation map of every group. Hence, active antennas and modulation type change according to different ACMM in Book, which makes it hard for the eavesdropper to know the right constellation map and can guarantee the security of the wireless communication.
At last, the constellation points are rotated randomly by K3and submitted through the submitting antennas.

Fig. 4. The constellation mapping of 3-D modulation (2 antennas, QPSK).
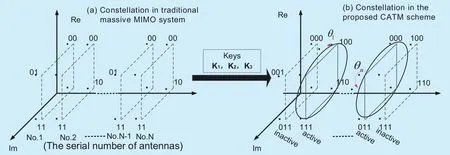
Fig. 5. The proposed CATMCPR scheme compared with the traditional massive MIMO.
Step 4. Demodulate at the receiver side. In this paper, we focus on the encryption algorithm at the physical layer, so we assume that the receiver can possess the right keys K1,K2and K3from the wireless channel. Thus,the receiving signals can be detected by the signal detecting algorithm illustrated in the next section. Finally, the original information bits are decrypted by taking the reverse of the operations in transmitting antennas.
3.2 Key generation algorithm
Many inherent properties of wireless channels at the physical layer, i.e., randomness, reciprocity and location-specific, make it possible to extract secret key from the properties of wireless channels. Fig. 6 shows the four steps of extracting secret key.
? Channel probing: This is a way to collect channel measurements by Alice and Bob.They transmit probing signals alternately and the CSI can be acquired by estimating.Because of channel reciprocity, highly correlated measurements can be observed by Alice and Bob.
? Measurement quantization: Each legitimate party quantizes the channel measurements into vector bits to obtain a preliminary secret key [23], [24].
? Information reconciliation: Due to the errors in channel probing, mismatched bits may exist in the preliminary secret key.Thus, the legitimate nodes exchange messages over the public channel to agree on a synchronized secret key, by error correction codes [25]. This is a form of error correction to ensure that the secret key generated at Alice and Bob separately are identical.
? Privacy amplification: This is a method for eliminating correlation among the bits and the partial information about the secret key that is intercepted by the adversary [26].
The secret keys extracted from the wireless channel are transformed into the initial value of the chaotic system. The chaotic system has the desirable properties of pseudo randomness,unpredictability, broadband spectrum, periodicity and high sensitivity to the initial value and system parameters [27]. So we choose a typical chaotic system, named Lorenz chaotic system, which is defined as:
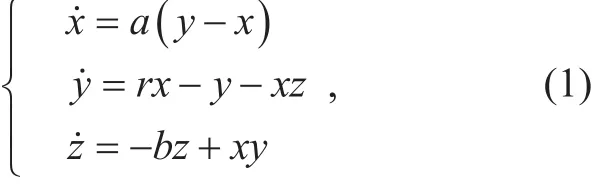
where a, r, b are system parameters, and x,y, z are variables. In the case of parameters a=15, b=7/3, r=26, the solutions of Lorenz chaotic system are chaotic sequences containing multi-period windows. Furthermore, the solutions jump between two singular points.The phase space diagram of Lorenz chaotic system is shown in figure 7.
In this paper, the initial values of x, y and z extracted from the wireless channel are substituted into Lorenz chaotic system to generate a chaotic sequence. Then we quantify the chaot-ic sequence as three binary sequences with an appropriate quantization method [28]. Finally,the secret keys K1, K2and K3consist of three chaotic binary sequences respectively.
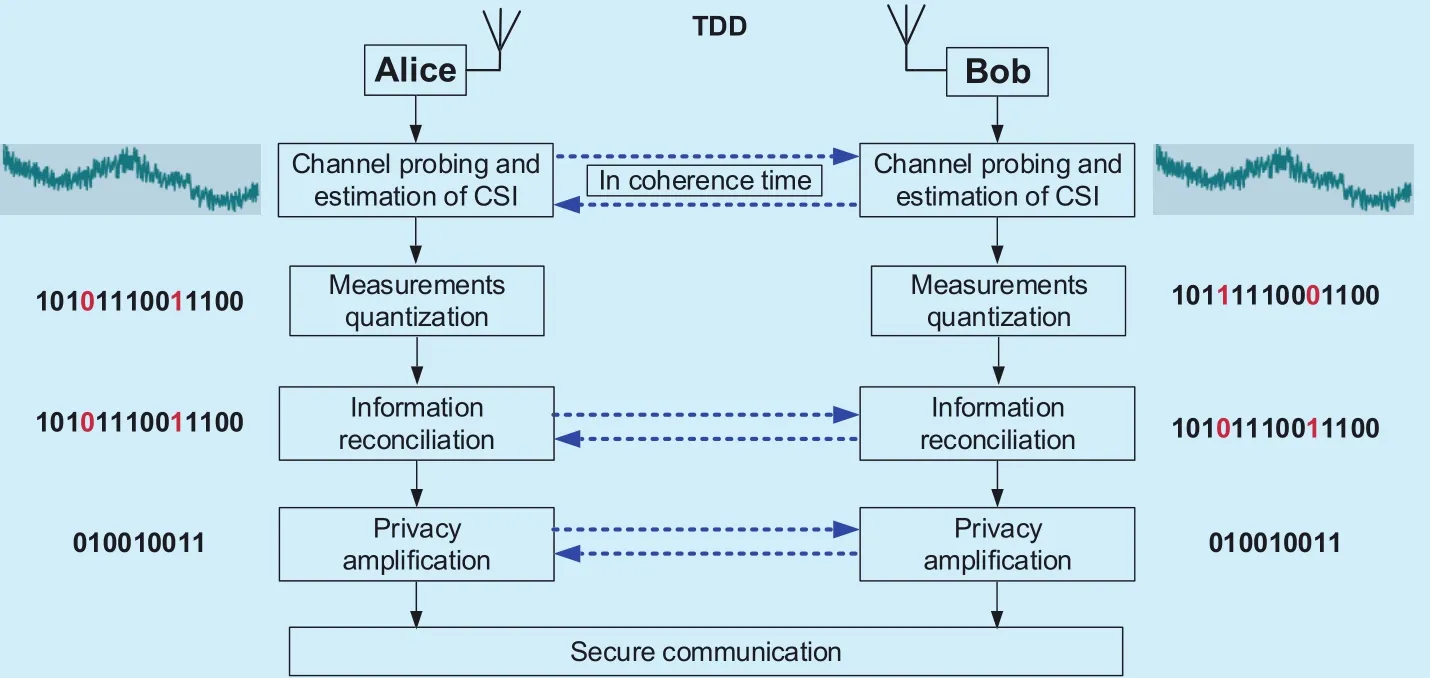
Fig. 6. The process of extracting secret key from channel state information (CSI).
3.3 Detecting algorithm at Bob
The serial number of activated antennas and the constellation points should be detected at Bob. At first, the Energy Detection (ED)method is used to detect the serial number of activated antennas. Then, the minimum mean square error estimation with successive interference cancellation (MMSE-SIC) detection scheme [29] is used to decode the constellation points.
The Energy Detection method is introduced as follows. After compensating for the rotating of the constellations, the input waveform in the decision devise can be expressed as:
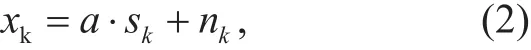
where k is the serial number of the antenna, xkis the constellation point transmitted on the k th antenna, a is the complex-valued channel gain, and nkis the Gaussian noise.If antenna k is not activated, sk=0. On the contrary, sk≠0. Assuming that the CSI is perfectly known, we can perform data detection.In fact, we should do this for the more relevant case of frequency selective channels; the signal model would be:

where Hkis the channel gain on the k th antenna. To detect the active antennas first, as we know that there are exactly N/2 of them, we could simply select the N/2 antennas which correspond to the top N/2 magnitudes of the|xk|′ s.
According to the Energy Detection method mentioned above, we can get the serial number of the N/2 activated antennas. Then,MMSE-SIC is used to decode the constellation points on the N/2 activated antennas. Finally, the original information bits are decrypted by taking the reverse of the operations in transmitting antennas.
IV. PERFORMANCE EVALUATION AND SIMULATION RESULTS
In this selection, we illuminate the advantage of this algorithm through theoretical analysis and simulation results. The simulation conditions are shown in table 1. It is assumed the channel is perfectly known at the transmitter and legitimate receiver, which means that the secret keys K1, K2and K3can be synchronized between Alice and Bob correctly. In the massive MIMO system, the encoding scheme of transmitter is Vertical-Bell Laboratory layered space-time (V-BLAST) encoding architectures, and the decoding scheme of receiver is MMSE-SIC decoding algorithm. The following section will make analysis and simulation results on the security, energy efficiency and reliability respectively.
4.1 Analysis on the security and complexity
According to the Kerckhoffs principle [30], it is assumed that the receiving capacity of the eavesdropper and the legitimate receiver are the same. Furthermore, Eve has powerful computing power and can do exhaustive attack.Due to the fact that the encryption method is fully open, the security of the system does not depend on the confidentiality of the method.
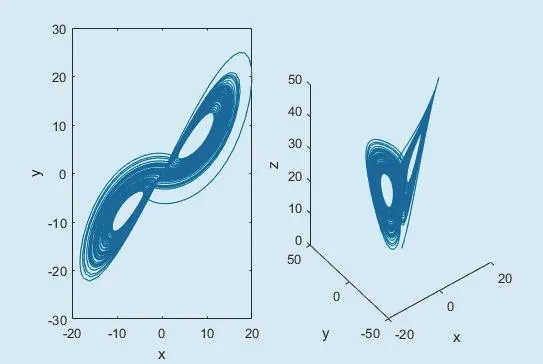
Fig. 7. The phase space diagram of Lorenz chaotic system.
4.1.1 Algorithm security proof
The security of ACTM derives from two encryption processes. First, the corresponding relationship between ACMM and the memory addresses in Book is scrambled by K2, and a certain ACMM is selected by K1. Second, the constellation points are rotated randomly by K3.
Considering the first encryption process,computational complexity mainly comes from the process of finding the right ACMM that is used by Alice to encrypt the original information bits. For Eve who is unknown to K1and K2, all of the ACMMs in Book should be traversed. Thus, the computational complexity of Eve is O((N?1)!!×(2M)!). For Bob who can get the right K1and K2, the right ACMM can be find directly. The comparison of computation complexity at Bob and Eve with different number of transmitting antennas (N) and modulation order (M) is shown in Table 2, where the unit is the time required for an addressing operation. As it can be seen from Table 2, the computation complexity of Eve increases sharply with the increasing ofN and M. By comparison, Bob only needs to recover the corresponding relationship between ACMM and the memory addresses in Book by K2and find the memory address by K1, which is just one addressing operation.
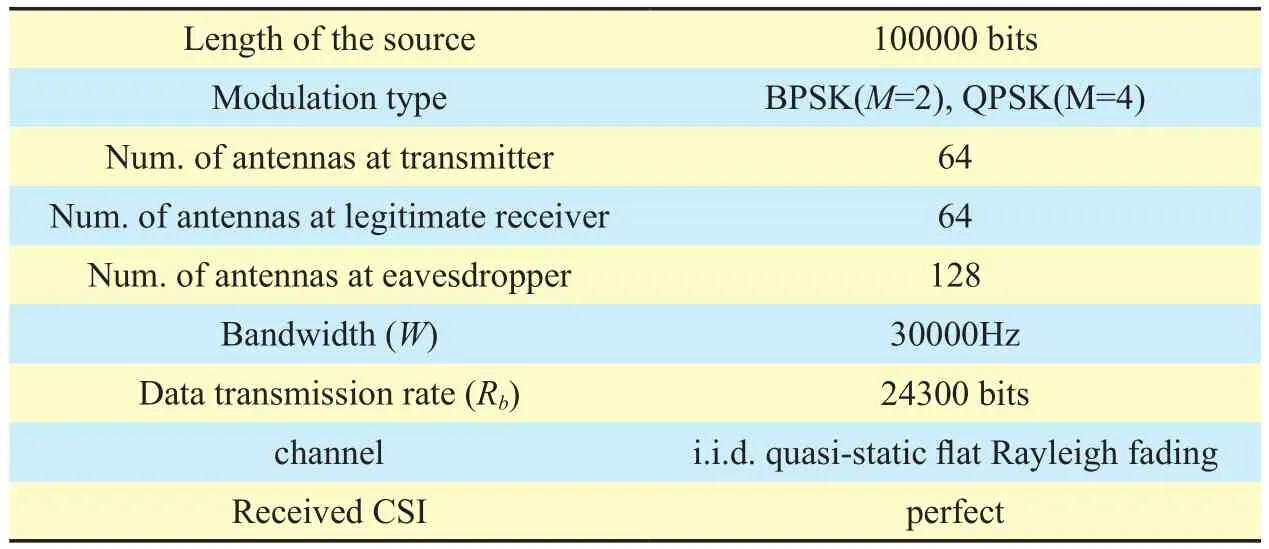
Table I. Simulation parameters.
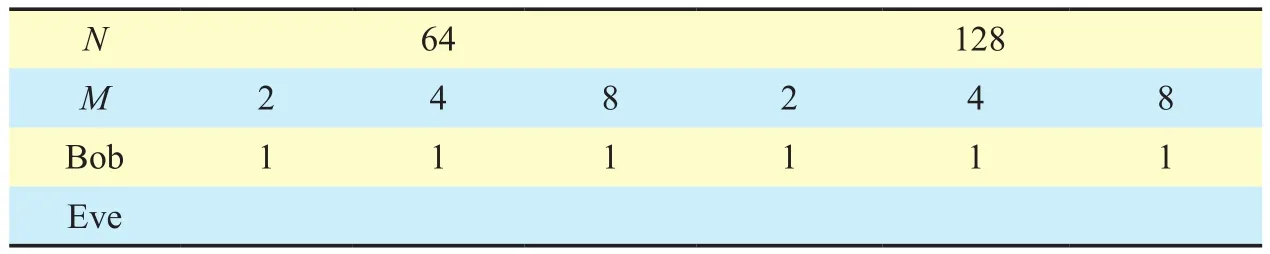
Table II. The comparison of computation complexity at Bob and Eve.

Table III. SER of the massive MIMO eavesdropper.
In terms of the second encryption process,the constellation points are rotated randomly by K3. We consider a practical case that the information bits are modulated by QPSK; thus the constellation points are
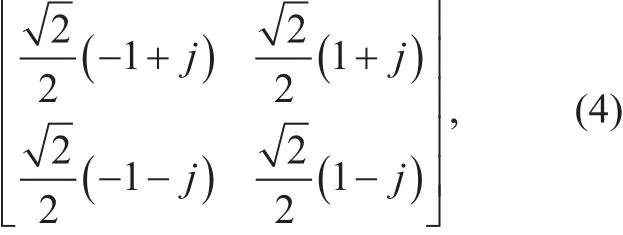
where the modulated symbol power is normalized. Note that if<∠<, then the original symbol will be rotated to another quadrant, where ∠K3denotes the phase of the complex matrix K3. Otherwise, the original symbol will not be rotated. In this section,we assume that Eve can intercepted the rotated symbol perfectly. Thus, the symbol error rate(SER) of Eve is equal towhich is the probability that the original symbol will be rotated to another quadrant. We emphasize that if ∠K3is uniformly distributed over the range [0,2]π, the SER Pe,SERof Eve is given by
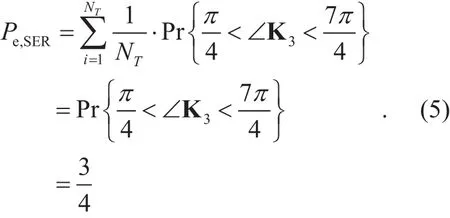
The simulation result of Eve’s SER is listed in Table 3. The original symbols of QPSK are in the first constellation quadrant, which is. For the 10000 test symbols, only 2519 received symbols are still in the first quadrant, which means the SER of Eve is 0.7481 or approximately 0.75. In addition, Eve fails to recognize the modulation type by the higher order statistics (HOS), which is the most popular modulation classification method [31].
Both theory analysis and simulation results show that the second encryption process can protect the original symbols from being intercepted by Eve.
According to the above analysis, the key point of the encryption’s security relies on the randomness and uniformity of key sets K1,K2and K3, which will be analyzed in the next section.
4.1.2 Random analysis of cipher text
In the secure communication, the cipher text is required to meet the randomness test for ensuring that the eavesdropper cannot obtain any statistical rules from the cipher text. Currently widely used standard test suite is designed by the National Institute of Standards and Technology (NIST), including a total of frequency test, run test, approximate entropy test and other 12 different indicators mentioned in[29]. The standard uses a certain test algorithm by comparing the degree of deviation between the sequence to be tested and the ideal random sequence, getting the p-value(p-value∈[0,1]). To pass the test, all p-values must be larger than 0.01. We check the randomness of cipher streams and calculate the p-values, the parameters and the results are listed in table 4 and table 5, respectively. As it can be seen from table 5, all p-values of the test items are great than the significance level which shows that the round keys generated by chaotic sequence have a certain randomness.
4.2 Analysis on reliability
Fig. 8 and figure 9 show the reliability simulations of the BER performance comparison of the CATMCPR scheme and the conventional massive MIMO system which uses 64x64 antennas, V-BLAST encoding algorithm and MMSE-SIC decoding algorithm. In addition,the only distinction is that the traditional massive MIMO system does not utilize the encryption and decryption algorithm in the CATMCPR scheme.
As is depicted in figure 8 and figure 9,Eve’s BER performance stays about 0.5 in spite of the SNR of the received signal, which is far worse than Bob’s. That is to say, Eve cannot decode any information from Alice to Bob which demonstrate the security of the CATMCPR scheme. On the other hand, compared with the conventional massive MIMO,Bob’s BER performance of CATMCPR scheme is much better. When modulation type is BPSK, the performance gain is about 8dB and 10dB at BER 10?2and 10?4. And when modulation type is QPSK, CATMCPR brings about 10dB performance improvement at BER 10?2. According to the trend of the curves, the BER performance improves faster with the increasing of SNR.
The main reason why Bob’s BER performance of CATMCPR scheme is much better than the conventional massive MIMO is spatial diversity gain, which can reduce the impact of multipath fading. In an NR×NTMIMO system with MMSE-SIC decodingalgorithm, the spatial diversity order, which denoted by Nd, is given by
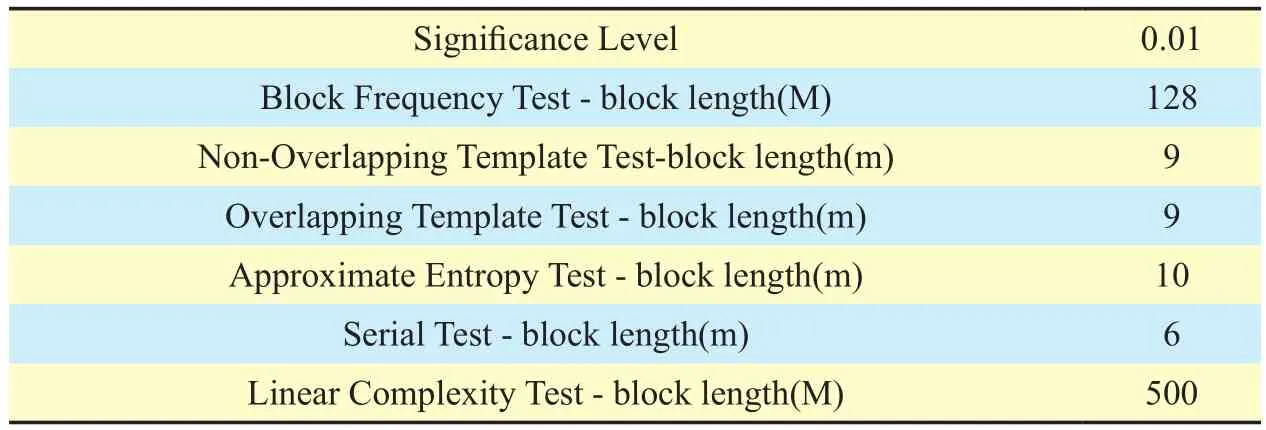
Table IV. NIST parameter setting.
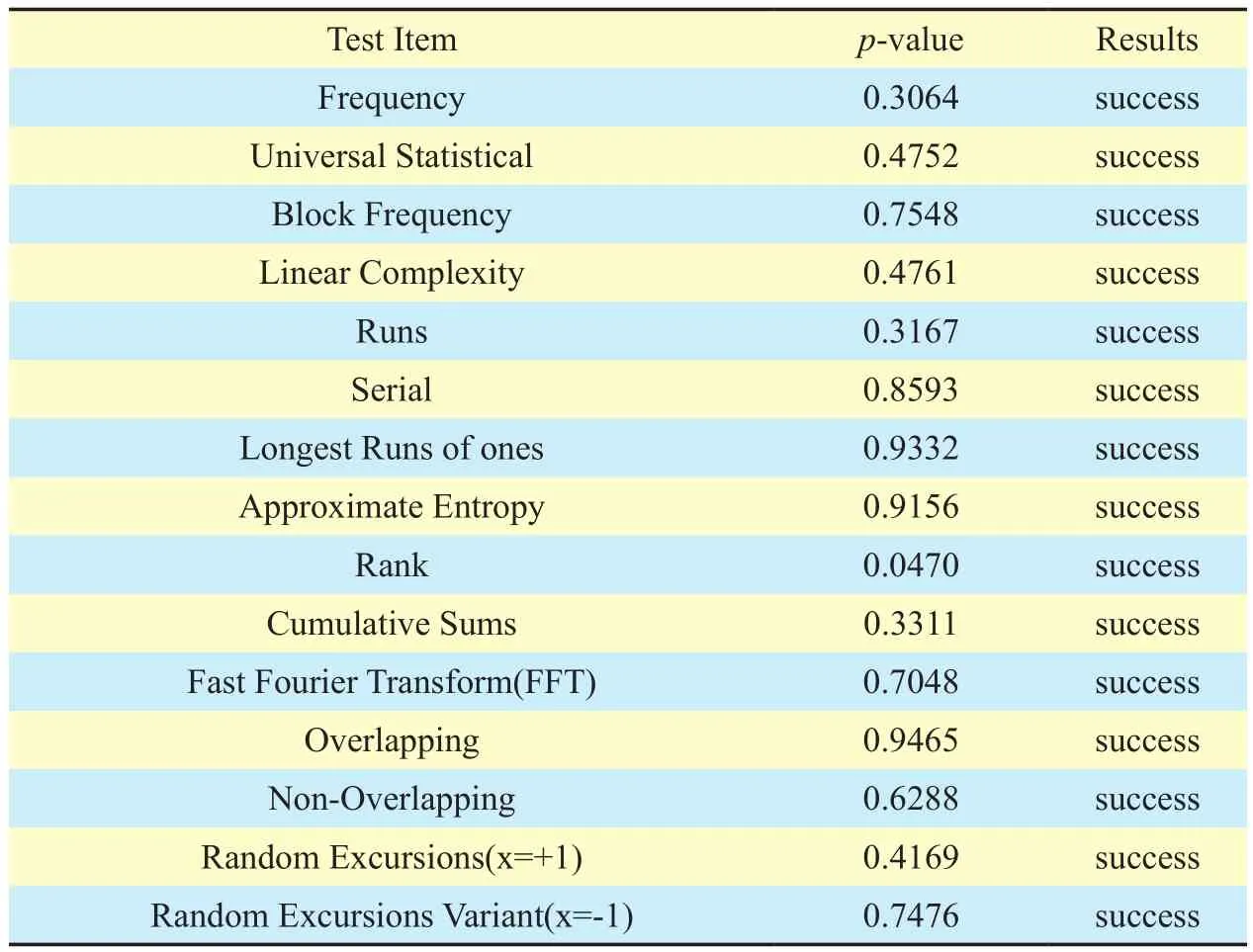
Table V. NIST random test results.
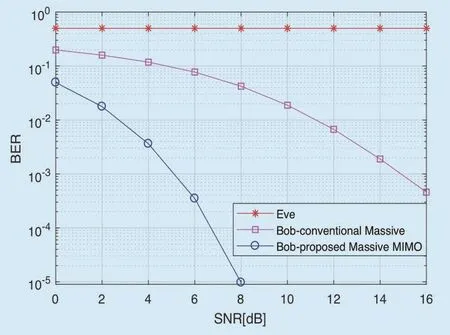
Fig. 8. BER performance comparison of the CATMCPR scheme and the conventional massive MIMO (BPSK).
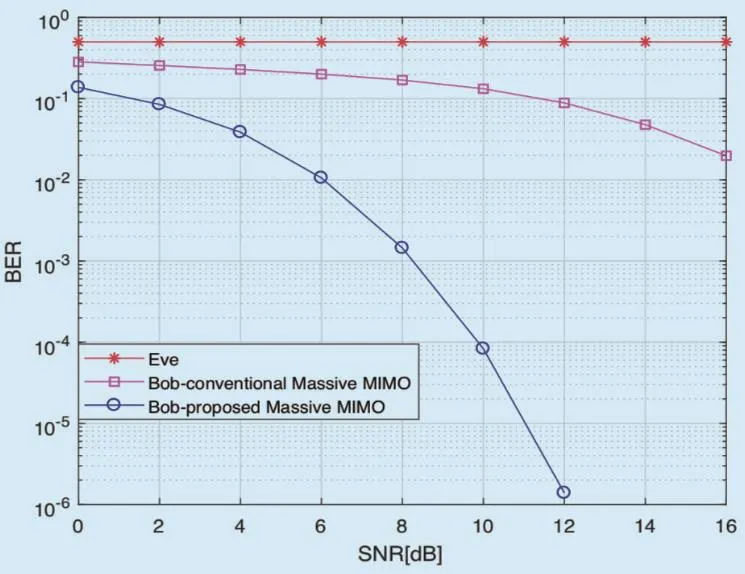
Fig. 9. BER performance comparison of the CATMCPR scheme and the conventional massive MIMO (QPSK).
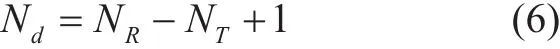
Therefore, for the conventional 64x64 MIMO, Nd=1. By comparison, in the CATMCPR scheme, where only 32 transmitting antennas are activated and 64 receiving antennas are used to decode the received signals,Nd=33. For a given SNR, the BER decreases as Ndincreases due to the fact that the performance of combating multipath fading improves as Ndincreases [29]. Furthermore, as the number of transmitting antennas becomes less and the number of receiving antennas becomes more, the transmitting antenna interference decreases and the receiving antennas can reduce the interference more effectively,which brings Bob’s BER performance improvement.
4.3 Analysis on spectral efficiency and energy efficiency
We define the spectral efficiency (ηSE) as

and the energy efficiency (ηEE) is given by

where ω represents the energy consumption of a transmitting symbol slot.
According to the simulation parameters, the number of antennas, W and Rbare the same in the CATMCPR scheme and the conventional massive MIMO. In order to compare the energy efficiency, we define rEE,rSEand rECare the ratio of the energy efficiency, spectral efficiency and energy consumption respectively between the CATMCPR scheme and the traditional massive MIMO. Note that in traditional massive MIMO all N transmitting antennas are used to transmit symbols, where the maximum effective information bits (R1)are given by
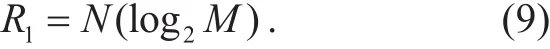
By comparison, in the CATMCPR scheme,only half of the N transmitting antennas are used to transmit symbols, where the maximum effective information bits (R2) are given by
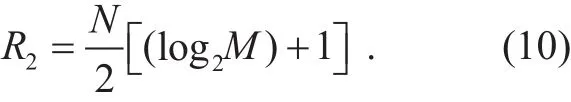
Assuming there is no error in transmission process, rE′E, rSEand rECshould be calculated as:
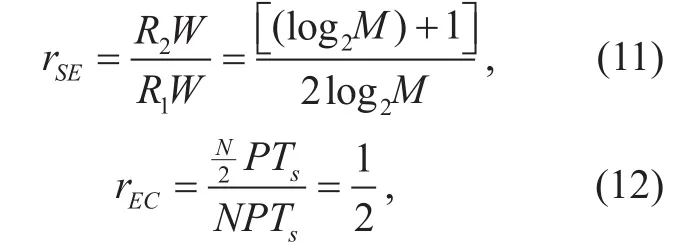
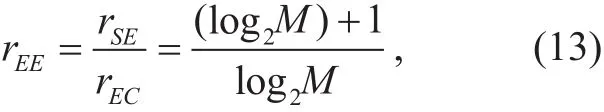
where P represents the energy required for transmitting each symbol.
In order to make the analysis more comprehensive, we consider the SM-MIMO physical-layer security scheme mentioned in [22]as a contrast, which is a typical physical-layer security method in SM-MIMO system. In this scheme, only a single TA is used to transmit modulated signal in every channel use and other TAs are used to transmit jamming signal.Note that the secrecy enhancement comes at the cost of multiple active RF antennas and excess jamming power. The simulation parameters are the same as Table 1.
In this scheme proposed in [22], only one transmitting antenna are used to transmit symbols, where the maximum effective information bits (R3) are given by
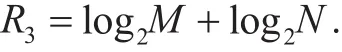
For this scheme, the higher the excess jamming power, the higher the secrecy rate.Here, we assume that the excess jamming power is equal to the modulated signal power.We define rE′E, rS′Eand rE′Care the ratio of the energy efficiency, spectral efficiency and energy consumption respectively between the CATMCPR scheme and the scheme proposed in [22].
Assuming there is no error in transmission process, rE′E, rS′Eand rE′Cshould be calculated as:
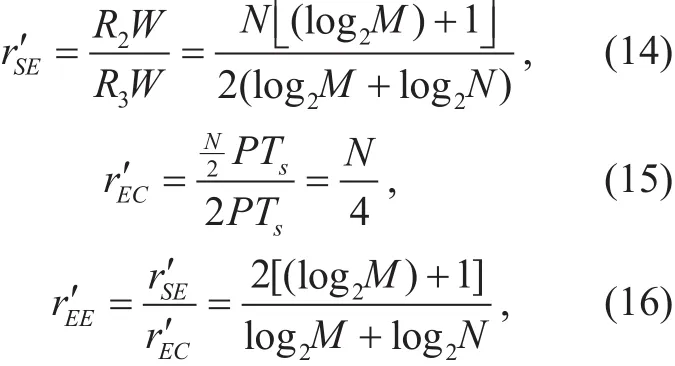
where P represents the energy required for transmitting each symbol.
The results of rEE, rSE, rE′Eand rS′Ewith different modulation order and N=64 is depicted in figure 10. Compared with the conventional MIMO system, rSEand rEEincrease as modulation order decreases. Note that rEEis always larger than 1, which means ηEEof CATMCPR scheme is always higher than traditional MIMO system’s. Thus, the CATMCPR scheme has a significant advantage in saving energy (saved energy nearly a half compared with the traditional MIMO) at a little cost of SE in a no error channel. Note that more energy can be saved as modulation order decreases, which makes the CATMCPR scheme a green secure transmission scheme with higher EE.
Compared with the SM-MIMO physical-layer encryption scheme proposed in [22],rS′Eand rE′Eincrease as modulation order increases. Note that rS′Eis always larger than 8,which means ηSEof CATMCPR scheme is always much higher than traditional SM-MIMO physical-layer encryption scheme’s. Furthermore, when, ηEEof CATMCPR scheme is just a little bit lower than traditional SM-MIMO encryption scheme’s. And when, rE′E> 1 . That is to say, the CATMCPR scheme has a signifi-cant advantage in improving SE at a little cost of EE in a no error channel compared with traditional SM-MIMO encryption scheme.
According to the EE and SE analysis of the CATMCPR scheme with different modulation order, conventional SM-MIMO physical-layer encryption scheme, we can conclude that the CATMCPR scheme is able to achieve higher SE compared with conventional SM-MIMO physical-layer encryption scheme. Furthermore, it can keep the high EE feature of SM.
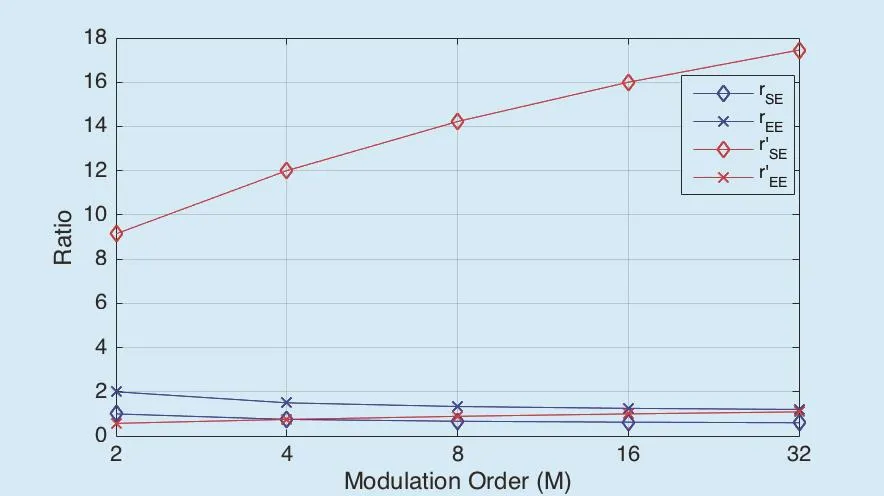
Fig. 10. rEE, rSE, rE′E and rS′E with different modulation order.
V. CONCLUSION
In this paper, we proposed a novel physical layer encryption scheme called CATMCPR to defend against eavesdroppers equipped with massive antennas and improve the energy efficiency in massive MIMO by using chaotic antenna-index and 3-D modulation. The proposed CATMCPR scheme has been introduced step by step. On the one hand, the CATMCPR scheme employs chaotic theory for generating keys to protect the mode of antennas combination and modulation type for obtaining the security of system. On the other hand, half antennas are activated for transmitting symbols,so it can have an obvious effect in improving SE compared with conventional ones. Lastly,we make an analysis on security, reliability and energy efficiency. We have shown that the powerful massive MIMO eavesdropper cannot recover the original information bits, even if equipped with infinite number of antennas,while the legitimate receiver is able to recover the original information bits correctly. Hence,the CATMCPR can achieve the physical layer security without a pre-shared secret key or prior CSI at the cost of little computational overhead. In addition, BER performance of the CATMCPR scheme has a significant improvement compared with conventional massive MIMO. Therefore, the security and reliability performance of the system is guaranteed to a large extent. Furthermore, both theoretical analysis and simulation results show that the CATMCPR scheme can improve the SE with the guarantee of high EE feature compared with conventional SM-MIMO physical-layer security schemes. Further research is to implement the CATMCPR scheme with FPGA and make a whole consideration about both encryption and key extraction.
ACKNOWLEDGMENT
This work was supported in part by the National Natural Science Foundation of China under Grant 61502518, 61372098 and 61702536.
- China Communications的其它文章
- A Precise Information Extraction Algorithm for Lane Lines
- Energy-Efficient Multi-UAV Coverage Deployment in UAV Networks: A Game-Theoretic Framework
- An Efficient Algorithm for Skyline Queries in Cloud Computing Environments
- Cryptanalysis of Key Exchange Protocol Based on Tensor Ergodic Problem
- A Robust Energy Efficiency Power Allocation Algorithm in Cognitive Radio Networks
- SVC Video Transmission Optimization Algorithm in Software Defined Network

