一道高三診斷題引發(fā)的推廣*
甘肅蘭州第五中學(xué)(730000)李守明
甘肅蘭州第五十二中學(xué)(730000)司 愷
題目(蘭州市2017年高考診斷考試?yán)砜频?0題)已知橢圓C:=1(a>b>0)經(jīng)過(guò)點(diǎn)且離心率為
(1)求橢圓的方程;
(2)設(shè)M,N是橢圓C上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足試探究:是否存在兩個(gè)定點(diǎn)F1,F2,使得|PF1|+|PF2|為定值?若存在,求F1,F2的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
1 試題來(lái)源及解答
該試題實(shí)際上是對(duì)重慶2011年高考理科20題的簡(jiǎn)單改變,原試題的題設(shè)條件為:橢圓的中心為原點(diǎn)O,離心率一條準(zhǔn)線的方程為原試題的問(wèn)法和本次診斷考試試題的問(wèn)法完全相同.作為高考試題,凝聚著命題者的智慧,對(duì)高中數(shù)學(xué)教學(xué)起著積極的導(dǎo)向作用,是教學(xué)研究的重要內(nèi)容,也成為各級(jí)考試爭(zhēng)相模仿和改編的素材,若我們能對(duì)高考試題進(jìn)行探究,剖析高考試題的本質(zhì),加深對(duì)問(wèn)題的理解,則會(huì)收獲意想不到的驚喜!下面給出本試題的解答:
解(1)
(2)設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·即x1x2+2y1y2=0,則由
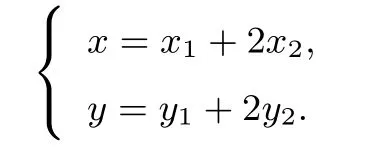

2 試題的推廣
推廣1設(shè)M,N是橢圓C:=1(a>b>0)上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由
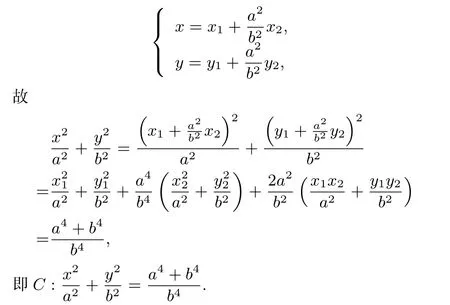
推廣2設(shè)M,N是雙曲線C:=1上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由
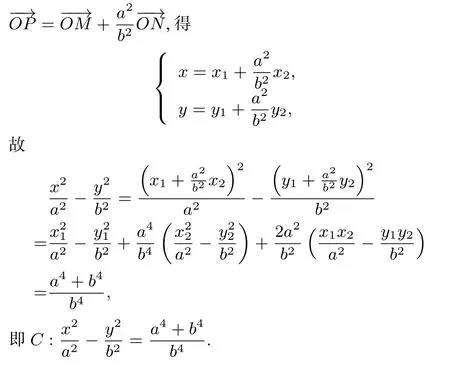
推廣3設(shè)M,N是橢圓C:上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由

故
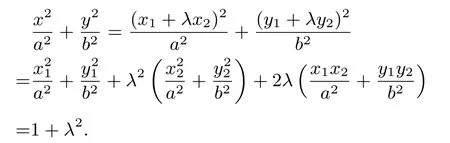
推廣4設(shè)M,N是雙曲線C:=1上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為C:
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由

故
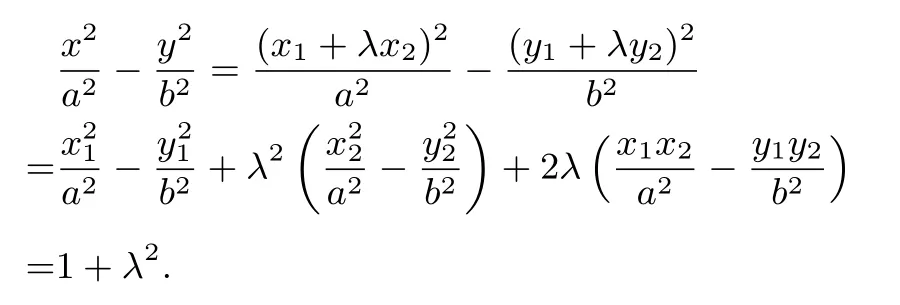
推廣5設(shè)M,N是橢圓C:上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為C:
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由
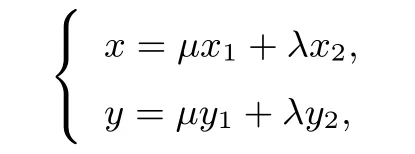
故
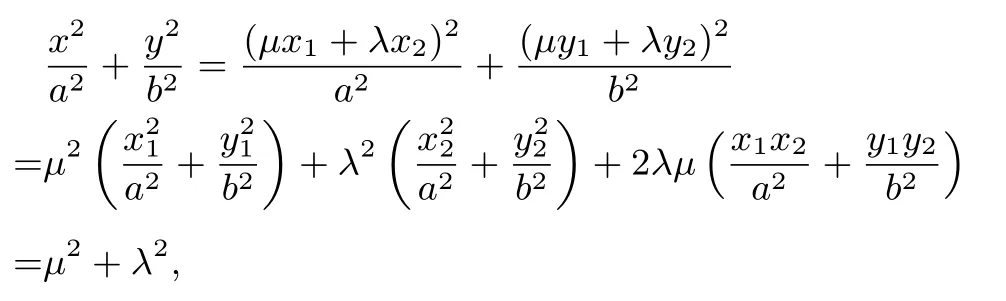
顯然是橢圓.
推廣6設(shè)M,N是雙曲線C:上的點(diǎn),直線OM與ON(O為坐標(biāo)原點(diǎn))的斜率之積為若動(dòng)點(diǎn)P滿足則點(diǎn)P的軌跡方程為C:
證明設(shè)P(x,y),M(x1,y1),N(x2,y2),依題意kOM·又由
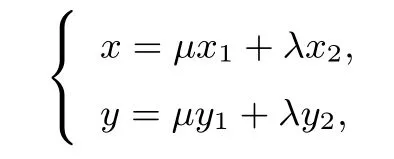
故
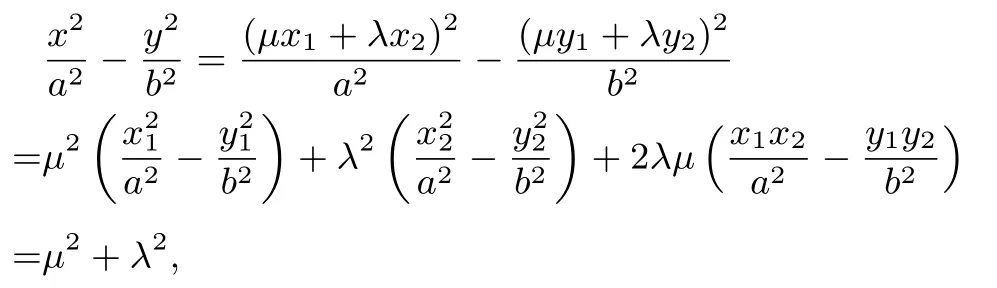
顯然是雙曲線.

