Chao Chen

Institute of Logic and Cognition,Sun Yat-sen University Department of Philosophy,Sun Yat-sen University

chench53.logic@gmail.com

1 Introduction

In this paper we propose an effective version of Differentiation Theorem for Approximate Identities.Recent results have shown that algorithmic randomness is a very useful tool to study the effective aspects of classical analysis.Many theorems have been investigated,including the ergodic theorem([1,4]),Lebesgue differentiation theorem([7])and many other topics([3,2]).Generally,these results have this form:

A realxhas a certain property that holds almost everywhere

?xsatisfies a certain randomness notion.

Approximate identity is a very important topic in the study of functional and harmonic analysis.The Differentiation Theorem for Approximate Identities is a basic theorem concerning approximate identity.It says that for ak∈L1with a radially decreasing majorant such thatkε=ε-1k(ε-1x),we havekε?f→f,for allxexcept a null set asε→0.

This theorem also indicate the Lebesgue differentiation theorem.It has been shown in[7]that the Lebesgue differentiation theorem can characterize Schnorr randomness.In this paper,our main result is that the Differentiation Theorem for Approximate Identities also characterize Schnorr randomness.And we will obtain an effective version of Lebesgue differentiation theorem which is slightly different from[7].

In section 2,we present the necessary preliminaries.Section 3 and 4 contain the proof of the two directions of our main theorem respectively.

2 Preliminaries

The classical version of the Differentiation Theorem for Approximate Identities can be found in[5].To introduce this theorem,we begin with some definitions:

Definition 1(convolution) Letf,gbe inL1(R).Theconvolution f?gis

Itisknownthatconvolutionsatisfiescommutativity,associativityanddistributivity.

Definition2Anapproximateidentity(asε→0)isafamilyofL1(R)functionskε(0＜ε≤1)with the following three properties:

·There exists a constantc＞0 such thatfor allε.

·for allε＞0.

·For any neighborhoodVof 0 we haveasε→0.

LetB(x,θ)be the neighborhood(x-θ,x+θ)andVcbe R-V.B(E,θ)denotes{y|?x∈E(|y-x|＜θ)}whereE?R.We useχAas the characteristic function ofA,whereA?R.Next comes the basic theorem concerning approximate identities:

Theorem 1([5])Letkεbe an approximate identity on R.

(1)Iff∈L1,then‖kε?f-f‖L1→0 asε→0.

(2)Iffis continuous in a neighborhood of a compact setEand bound on R,thenkε?fconverges uniformly tofonEasε→0.

In this paper we focus on a special kind of approximate identity.Letk(x)be a integrable function with integral one.Then we definekε:=ε-1k(ε-1x).It is straightforward to seekεis an approximate identity.

A functionfis called radial,iff(x)=f(y)whenever|x|=|y|.If suchfis decreasing on[0,∞)andf≥|g|in R,we callfa radial decreasing majorant ofg.

Definition 3(Dominated Approximate Identity) Given a functionk∈L1(R)such that,we callkεadominated approximate identityif:

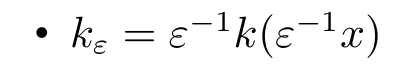
·khas a radial decreasing majorantKwhich is continuous except at a finite number of points.

Definition 4The function

is called thecentered Hardy-Littlewood maximal functionoff.Actually,if we define,then we have

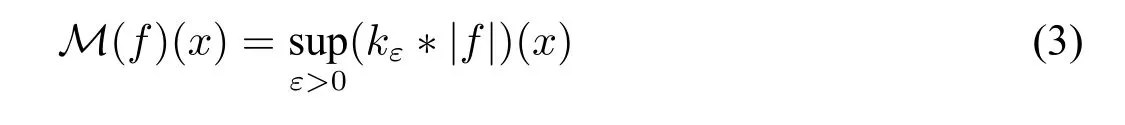
Here are two classical results which are useful in our proof.We refer to[5]for more details.

Lemma 1(2.1.12,[5]) Ifkεis a dominated approximate identity with the radially decreasing majorantK,then the estimate

is valid for all functionf∈L1(R).

Lemma 2(2.1.6,[5]) Iff∈L1(R),then

Next comes the differentiation theorem for approximate identities,which can be viewed as a generalization of Lebesgue differentiation theorem:

Theorem2(DifferentiationTheoremforApproximateIdentities,2.1.17,[5]) Letkbea dominated approximate identity with a radially decreasing majorantK.Thenkε?f→fa.e.asε→0 for allf∈L1(R).

Our job is to find the effective version of this theorem.The first thing we need to do is extending the computable notion from N to R.The next definitions can be found in[8].Letakbe a computable enumeration of all rationals on R.

Definition 5A real number is computable if there are two computable functionsh:N→N andd:N→N s.t.

This computable realxis coded by the indices ofhandd.Letrebe the computable real on R indexed bye.

Definition 6Eis a compact set on R.A functionf:E→R is computable if:·fis sequentially computable:there is a computable functionh:N→N s.t.f(re)=rh(e);·fis effectively uniformly continuous onE:there is a computable functiond:N→Q s.t.for allx,y∈E:

A functionf:R→R is computable if:

·fis sequentially computable:there is a computable functionh:N→N s.t.f(re)=rh(e);

·fis effectively uniformly continuous on every compact subset:there is a computable functiond:N2→Q s.t.for allx,y∈[-N,N]:

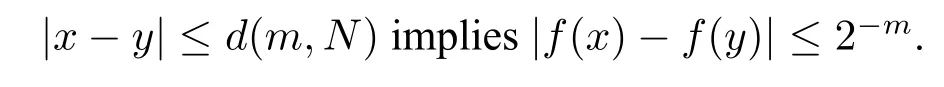
The computable functionfis coded by the indices ofhandd.Notice that for every[-N,N],the functions sup[-N,N](f)andfdxare uniformly computable onN.([8])A functionfis compactly supported,iff(x)=0 everywhere outside a compact set.

Definition 7Eis a compact set of R.A functionf:E→R isL1(E)-computable,orL1comp(E)for short if:there is a sequence of uniformly computable functionsfkonE→R and a computable functiond:N→N s.t.

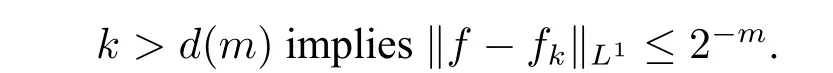
A functionf:R→R isL1(R)-computable,orL1comp(R)for short,if there is a sequence of uniformly computable compactly supported functionsfkon R→R and a computable functiond:N→N s.t.fkis supported on[-k,k]and:

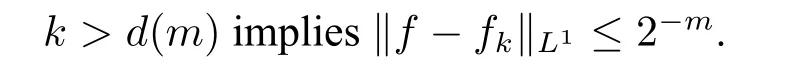
f∈L1comp(R)is coded by the indices offkandd.

It is easy to see that we can extend everyfunction to afunction uniformly.Notice that we actually define anL1-computable functionfas an equivalence class onL1.We will select a representativefrom such equivalence class such thathas a certain value whenxis Schnorr random.

Definition 8A sequence of setUn?R,n∈N is uniformly effectively open,or uniformly Σ1,if

wherean,i,bn,iis a double sequence of uniformly computable reals.

Based on the conception of uniformly effectively open sets,we can define different versions of algorithmic randomness.Intuitively,a real is random if it avoids all‘effectively null’sets.The most commonly accepted randomness notions are Martin-L?f randomness and Schnorr randomness.

Definition 9AMartin-L?f testis a uniformly Σ1sequence ofUn?R such thatμ(Un)≤2-nfor alln.A pointx∈R is said to pass the test ifx/∈∩nUn.xisMartin-L?f randomif it pass every Martin-L?f test.

ASchnorr testis a uniformly Σ1sequence ofUn?R such thatμ(Un)is uniformly computable onnandμ(Un)≤2-nfor alln.A pointx∈R is said to pass the test if.xisSchnorr randomif it pass every Schnorr test.

Theorem3(EffectiveWeierstrassTheorem,[8])EisacompactsetonR.AfunctionfonEis computable if and only if there is a computable sequence of rational polynomialspm(x)which converges effectively tofin uniform norm:there is a computable functiond:N→N such that|pm-f|≤2-nifm≥d(n).

A functionfon R is computable if and only if for anyN＞0 there is a computable sequence of rational polynomialspm,N(x)which converges effectively tofon compact set[-N,N]i.e.,there is a computable functiond:N×N→N such that|pm,N-f|≤2-nifm≥d(n,N).

Moreover,thepm(x)andpm,N(x)above can be obtained effectively from the index off.

According to effective Weierstrass Theorem,the‘a(chǎn) sequence of uniformly computable functions’in the definition ofL1-computable function can be replaced by ‘a(chǎn) sequence of uniformly computable rational polynomials’.

Lemma 3([7,9])Supposef∈L1comp[0,1]andfkis a sequence of uniformly computable rational polynomials such that‖f-fk‖L1≤2-k.

·(Existence)The limit limk→∞fk(x)exists on all Schnorr randomx.

·(Uniqueness)Given another sequence of uniformly computable rational polyno

mialsgksuch that‖f-gk‖L1≤2-k,

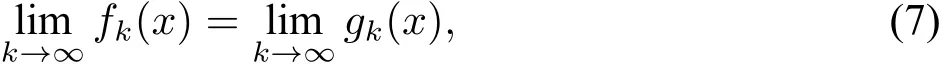
for all Schnorr randomx

It is straightforward to see the result above also holds inL1([-N,N]).Note that iffisL1(R)-computable,thenf?[-N,N]isL1([-N,N])-computable,so actually this result also holds inL1(R).We useto denote limk→∞fk(x)whenfkis the sequence as in the lemma above,which implies the value of(x)does not depend on the choice offkwhenxis Schnorr random.

A dominated approximate identitykεis computable ifkisL1-computable.Our main result is

Theorem 4(effective version of Differentiation Theorem for Approximate Identities)Letkεbe a computable dominated approximate identity.Thenfor allif and only ifxis Schnorr random.

We will use the following lemmas.

Lemma 4([7])Letsuch thatAnis uniformly c.e.andμ(An)is uniformly computable andμ(An)≤2-n.ThenAis c.e.andμ(A)is computable.Moreover,this holds uniformly.

Lemma 5([7,6])IfAandBare Σ1sets andμ(A)andμ(B)are computable,thenA∩BandA∪Bare Σ1sets andμ(A∩B)andμ(A∪B)are computable.

Letan∈R forn∈N and limnan=a.Then we say that it has a computable speed of approximation if there is a computable functionhs.t.for allk≥h(n)we have|ak-a|＜2-n.

3 Schnorr random points satisfy differentiation theorem for approximate identities

In this section we will prove that the differentiation theorem for approximate identities holds for all Schnorr randomx∈R.First,we show how it works whenfis computable on a compact set.

Lemma 6,thendyis a computable function ofxon R.In particular,is computable.

ProofSee[8].□

Lemma7 Letkεbe a computable dominated approximate identity.Eis a compact set andFisacompactneighborhoodofE,B(E,θ)?F,fiscomputableonFandbounded on R,i.e.there is aM＞0 s.t.|f|＜M.Thenkε?f→funiformly asε→0 onE.Moreover,the speed of this approximation is uniform computable onf?F,Mandθ.

ProofSincekεis a dominated approximate identity,letc=‖kε‖L1=‖k‖L1.Letη＞0 be an arbitrary real.We know that∫kε(y)dy=1,so we have

whereVis the neighborhoodB(0,δ).We need to find a sufficient smallδ＜1.Sincefis computable onF,there is aδsuch thaifx∈Eand|y|＜δ.So

for allx∈E.Notice that thisδdepends onθ.

We knowfhas a bound|f|＜M.Then

Sincekεis an approximate identity,the

It remains to calculate the speed of this convergence.Obviously it is determined by the speed of this convergence∫Vc|kε|dy→0 asε→0.For convenience we letδbe a rational.Replacet=ε-1ywe have

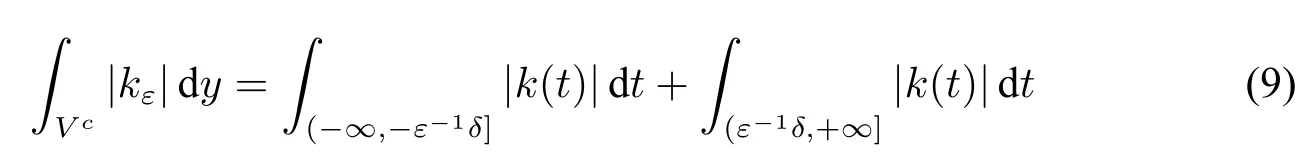
It is a computable function ofεby Lemma 6.So we useθandfto computeδ,then useδandkto find theε0to ensurefor allε≤ε0.We have

The following result can be viewed as an effective version of Egorov Theorem.

Lemma 8(Lemma 3.6,[7]) LetandE=[-N,N].fkis a sequence of uniformly computable rational polynomials onEsuch that

then there is a Schnorr testUmonEsuch that for anym,fk→uniformly onE-Um.Moreover,the speed of this convergence is uniform onm.

ByLemma3,weknowthatlimforSchnorrrandomx.Thefollowing lemma is very useful in our proof.

Lemma 9(Lemma 3.3,[7]) LetSbe a bounded set in R such thatSis first-order definableinthefieldofR.ThenthemeasureofSisacomputablerealnumber.Moreover,this holds uniformly on the first-order definition ofS.

Theorem 5Letkεbe a computable dominated approximate identity.Then for allf∈and Schnorr randomxwe have

Proof Notice that the valuekε?f(x)ignoresfon a null set of R,so we can assumef=without losing generality.The main idea is to prove the Lemma 8 also holds forkε?f(x)andkε?fk(x)for allε.We assumex＜N.LetEbe[-N,N]andfkbe the sequence of polynomials as in Lemma 8(fk=0 outsidesE).

Our idea is to construct such a chain asε→0 andn→∞:

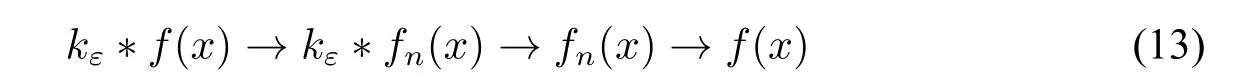
Firstly,let us deal with the first→.Notice that

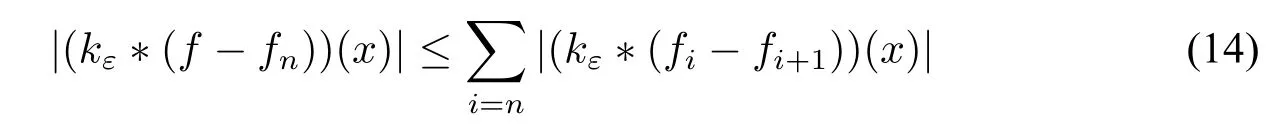
Sincekεis a computable dominated approximate identity,it has aL1-computable radial decreasing majorantK.SinceKcan be arbitrary large we can choose suchKthat‖K‖L1(R)=ais a rational.By Lemma 1 we have

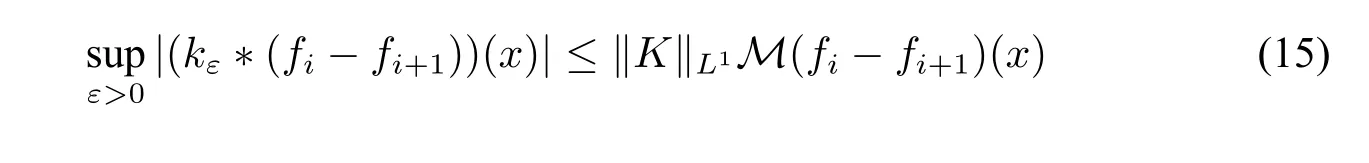
DefineAiasBy the definition we know

It is easy to see thatAiis uniformly first-order definable oni,so by Lemma 9μ(Ai)is uniformly computable oni.By Lemma 2 we have

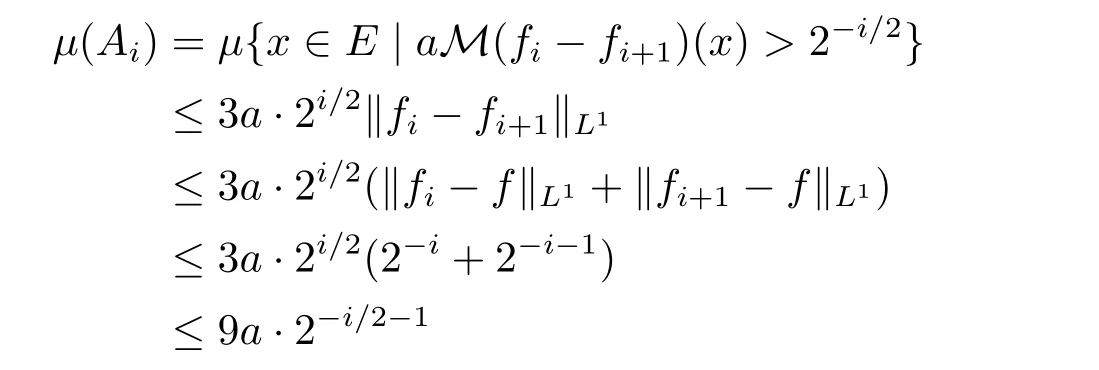
Let.It follows from Lemma 4 thatμ(Vs)is computable.We also have

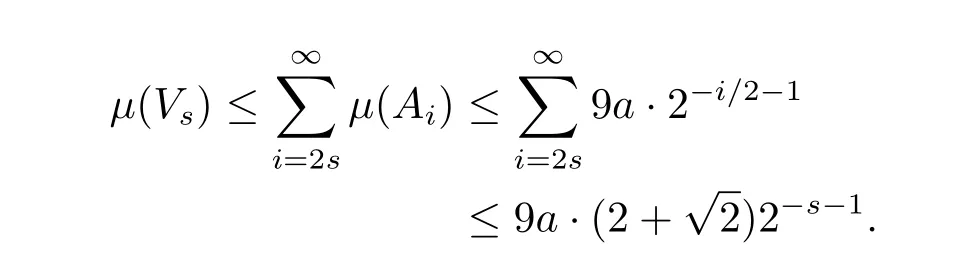
SoVsis a Schnorr test.Ifx/∈Vs,then for alli≥2s:

Combining with the definition ofMand triangle inequality we can have

LetGm=Vm∪UmwithUmas in Lemma 8.VmandUmboth have measure limits,so by Lemma 5Gmis a Schnorr test.Supposex/∈Gm.Fixδ,search a sufficient largensuch that|f-fn|(x)＜δ/3 and supε＞0|(kε?(f-fn))(x)|＜δ/3.Then by Lemma 7 there is a sufficient smallεsuch that|(kε?fn-fn)(x)|＜δ/3.Then we have

Thisδcan be arbitrary small so we conclude lim.This proves the required conclusion. □

4 The points satisfy differentiation theorem for approximate identities are Schnorr

In this section we will prove the converse part of the main theorem.Actually,we will show that ifxis not Schnorr random,the limit ofkε?f(x)may not exist.

Lemma 10Given a computable dominated approximate identitykε,kε?χA→0 asμ(A)→0.Moreover,the speed of this convergence does not depend on the specificA.

ProofSincekεisacomputabledominatedapproximateidentity,thereisaL1-computable radial decreasingKsuch thatK≥k.Note thatKε(x)≥Kε(y)when|x|≤|y|.We have

Hence,kε?χA(x)→0 asμ(A)→0.And the speed of this convergenceis uniform onε. □

We will show that our result hold for computablexfirst.

Theorem 6Given a computable dominated approximate identitykεand a computable realr,there is ansuch thatdiverges asε→0.

We will use the similar technic used in Lemma 4.5 in[7]to prove our theorem.

ProofSupposer＜Nfor some natural numberN.SetE=[-N,N].We will construct a uniformly computable sequence of 0,1-valued functionsfnon R such thatf=limfn.First,Letfn?Ec=0 for alln.So we only need to definefn?E.Letδbe a small positive rational.We will also construct an computable sequenceεnand an sequence of neighborhoodAnofrs.t.:Whennis even,kεn?fn(r)＜δandkεn?fn+1(r)＜δ;whennis odd,kεn?fn(r)＞1-δandkεn?fn+1(r)＞1-δ.

Conduct the induction onn.

The next stage is to find a rational neighborhoodA0?Eofrsuch thatμ(A0)＜2-1and|kε0?χA0|(r)＜δ.We definef1=f0+χA0.Sokε0?f1(r)＜δ.f1(x)=1 for allx∈A0,by Lemma 7 there is aε1such thatkε1?f1(r)＞1-δ.

Stagen+1.

·Assumeniseven.ApplyLemma10toobtainarationalneighborhoodAn?An-1ofrsuch thatμ(An)＜2-n+1and|kεn?fn|(r)+|kεn?χAn|(r)＜δ.Letfn+1=fn+χAn.So we still havekεn?fn+1(r)＜δ.Note thatfn+1(x)=1 forx∈An,wecanapplyLemma7toobtainanεn+1suchthatkεn+1?fn+1(r)＞1-δ.

· Ifnis odd,then we need theAnsatisfy|kεn?fn|(r)-|kεn?χAn|(r)＞1-δ.Letfn+1=fn-χAn.Here we havefn+1(x)=0 onAn,so we can obtain anεn+1such thatkεn+1?fn+1(r)＜δ.

So actually for everyn,we definefn+1?An=1-fnandfn+1?Acn=fn.By this construction we have

which means thekεn?fnis always close enough tofnandAnis too small to change it.

ItiseasytocheckthatfnisuniformlyL1-computable.Definefasf(x)=limn→∞fn(x).We needf∈L1compso it does not matterfis undefined on a null set.Since‖f-fn‖L1＜μ(An-1)＜2-n,we knowfis aL1-computable function.This sequencekεn?f(r)diverges since for allnit is always betweenkεn?fn(r)andkεn?fn+1(r),that is,kεn?f(r)＜δwhennis even,andkεn?f(r)＞1-δwhennis odd. □

A finite decimal is a real with the form 2-nkand a decimal intervalIis an interval on R with the form[2-nk,2-n(k+1)]wherenis a natural number andkis a integer.A decimal interval can be viewed as a interval on Cantor space.Two intervals are said to bealmost disjointif their intersection has at most one element.It is known that for any Σ1setU,there is a uniformly computable decimal intervalIisuch thatandare almost disjoint.

Lemma 11Letkεbe a computable dominated approximate identity.Eis a compact set andFis a neighborhood ofE,B(E,θ)?F.fis constant onFand 0,1-valued on R.Then there is a computable functionS:R+×R+→R+such that for allε≤S(θ,δ)we have

onE.

ProofIt is a straight forward conclusion from the proof of Lemma 7.Note that this functionSonly depends on the majorantK. □

Theorem 7Given a computable dominated approximate identitykεand a Schnorr testGm,we can construct asuch thadiverges for alwherexis not finite decimal.

We will modify the technic used in theorem 6 to construct the desiredf.

ProofSetE=[-N,N],clearlyGm∩EisaSchnorrtest.Sowithoutlosinggenerality we can assume thatx∈Gm?Efor allm.We will construct a sequence of 0,1-valued functionfnandf=limfn.Letfn?Ec=0 for alln.Letδbe a small positive real.

Stagesuch thatI0,iare almost disjoint decimal interval.fn(x)=0 for allx∈E.

Just like the proof of previous theorem we need to find anεsuch thatkε?fis close enough tofon an intervalI,but this generalεdoes not exist.Actually,we need to cut eachIinto infinite parts,and find a specificεfor each part.

Stagesuch thatIis a computable sequence of pairwisen,ialmost disjoint decimal intervals.Fixi,letl,k∈N andIn,i=[2-lk,2-l(k+1)].We defineaj∈In,iforj∈Z as follows:

·a0is the midpoint ofIn,i:

·Forj＞0,ajis the midpoint of[aj-1,2-l(k+1)]:

·Forj＜0,ajis the midpoint of[2-lk,aj+1]:

Then we defineJj=[aj,aj+1].To eachjwe define anεj.By the property of approximate identity,findεjs.t.for allx∈Jjandεjsatisfiesεj≤S(μ(Jj)/2,δ/2)withSdefined in Lemma 11.

Apply Lemma 10 to obtainαjsuch that|kεj?χA|≤δ/4 ifμ(A)≤αj.Then we effectively find a large integermjsuch that

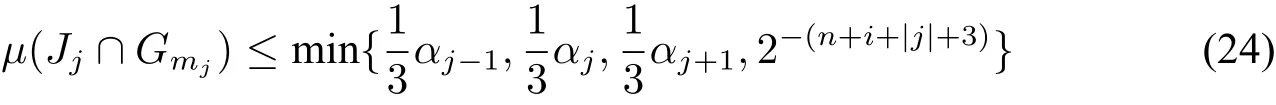
Let.We construct suchHn,ifor alli∈N.Then define

Let

Due to the construction ofUn+1we knowμ(Un+1)≤2-nfor alln＞0.So by the same argument of the previous theorem we concludef=limfnisL1-computable.

It remain to show thatkε?fdiverges a.SupposeUn.Letεjbe the real as in our construction.By the definition of functionSWe have.Notice that,we then have

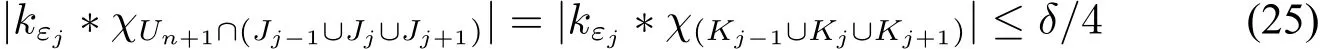
Combining the definition ofεjit follows that

which means thekεj?fnis always close enough tofnandUn+1is too small to change it.So

Thus for all,we have

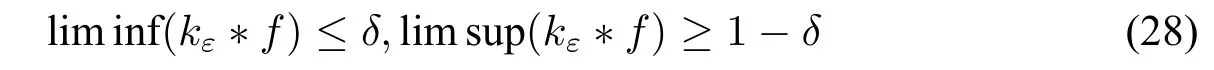
Thus,kε ?fdiverges atxasε→0.□

Let the functionkbe,we have this result directly:

Corollary 1

holds for all functionsif and only ifxis Schnorr random.

This effective version of the Lebesgue differentiation theorem is slightly different from[7]:

Theorem 8 ([7])

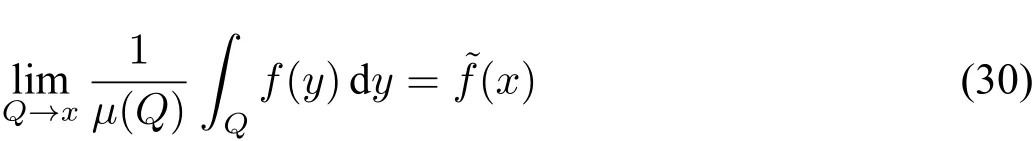
holds for all functionsif and only ifxis Schnorr random.

Compared with this theorem,our effective version of Lebesgue differentiation theorem requires thexto be the ‘center’ofQ,and also extends the theorem from[0,1]to R.

[1]L.Bienvenu,A.R.Day,M.Hoyrup,I.Mezhirov and A.Shen,2012,“A constructive version of Birkhoff’s ergodic theorem for Martin-L?f random points”,Information and Computation,210:21-30.

[2]L.Bienvenu,R.H?lzl,J.S.Miller and A.Nies,2014,“Denjoy,Demuth and density”,Journal of Mathematical Logic,14(01):1450004.

[3]V.Brattka,J.Miller and A.Nies,2016,“Randomness and differentiability”,Transactions of the American Mathematical Society,368(1):581-605.

[4]J.Franklin,N.Greenberg,J.Miller and K.M.Ng,2012,“Martin-L?f random points satisfy Birkhoff’s ergodic theorem for effectively closed sets”,Proceedings of the American Mathematical Society,140(10):3623-3628.

[5]L.Grafakos,2008,Classical Fourier Analysis,New York:Springer.

[6]M.Hoyrup and C.Rojas,2009,“Computability of probability measures and Martin-L?f randomness over metric spaces”,Information and Computation,207(7):830-847.

[7]N.Pathak,C.Rojas and S.Simpson,2014,“Schnorr randomness and the Lebesgue differentiation theorem”,Proceedings of the American Mathematical Society,142(1):335-349.

[8]M.B.Pour-El and J.I.Richards,1989,Computability in Analysis and Physics,Berlin:Springer-Verlag.

[9]J.Rute,2012,“Algorithmicrandomness,martingalesanddifferentiability”:http://www.personal.psu.edu/jmr71/preprints/RMD1_paper_draft.pdf.