Yang Zhao·Shuhong Dong·Peishi Yu·Junhua Zhao

1 Introduction

Graphene, a single-atom-thick, two-dimensional carbon material,has been extensively studied because of its remarkable electrical and mechanical properties[1–3].The tensile stiffness and strength of graphene sheets are on the order of 1TPa and 100GPa[4,5],respectively,which makes graphene one of the best candidate materials for reinforced nanocomposites[6]and nanoelectro mechanical devices[7].

To design and assemble graphene-based nanodevices,it is necessary to understand the mechanical properties of graphene under different loading conditions.Great effort has been made to identify the mechanical properties of graphene.The work of Leeet al.[4]measured the elastic properties and the intrinsic breaking strength of free-standing monolayer graphene membranes by nanoindentation test.Then Tan et al.[8]further studied the Young’s modulus of monolayer graphene by molecular dynamics(MD)simulations.Furthermore,M in and Aluru[9]derived the mechanical properties(such as shear modulus,shear fracture strength,and shear fracture strain)of zigzag and armchair graphene sheets.The work of Yeh et al.[10]revealed the theoretical foundation for strain-engineering of the electronic properties of graphene and then provided experimental evidence for strain-induced pseudo-magnetic fields and charging effects in monolayer graphene.In their study,Xu et al.[11]proposed a nonlocal continuum orthotropic plate model to study the vibration of orthotropic graphene sheets based on an analytical symplectic approach.Also,Nguyen et al.[12]studied the difference of vibration among graphene,SiC,and BN nanosheets using MD simulations.

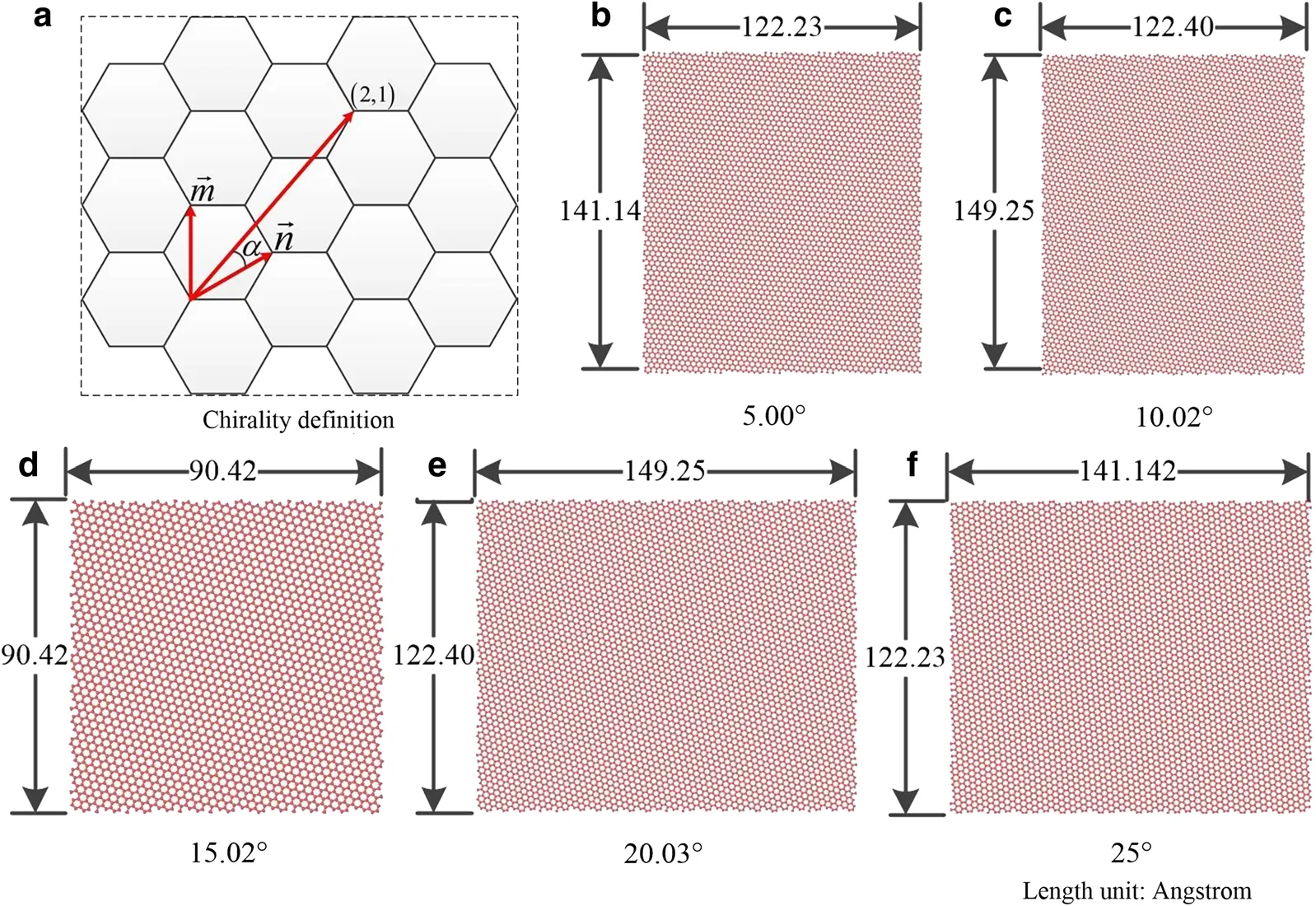
Fig.1 The definition of the chiral angleα and atomic structures of different chiral angles.a Definition of the chiral angleα.bα =5°.cα =10.02°.d α =15.02°.e α =20.03°.f α =25°

However,the shear behavior of chiral graphene sheets has been not clear yet.The work of Chang[13] firstly found that the torsional behavior of chiral single-walled carbon nanotubes(SWCNTs)strongly depends on the loading direction,in which the critical buckling shear strain of a SWCNT in one direction can be 1.8 times higher than that in the opposite direction.Because of a similar lattice structure with a corresponding chiral SWCNT,the shear behavior of a chiral graphene sheet is also dependent on its chirality and the loading direction.Recently,Yi and Chang[14]have studied the mechanical properties of chiral graphene sheets using molecular mechanics,where the temperature is zero and a finite graphene sheet under free boundary condition is considered.In fact,the finite graphene sheet is not under ideally pure shear deformation.Without loss of generality,it is significant and necessary to understand the shear behavior of chiral graphene sheets under pure shear deformation.Therefore,the atomic structures of chiral graphene sheets must meet periodic boundary conditions along both width and length directions.

In this study,the loading direction-dependent shear behavior of single-layer chiral graphene sheets under pure shear deformation at different temperatures is studied by MD simulations.Our results show that the shear properties of chiral graphene sheets strongly depend on the loading direction due to the structural asymmetry.The amplitude to wavelength ratio of wrinkles for different chiral graphene sheets under shear deformation using MD simulations is in good agreement with that from the existing theory.

2 Molecular dynamics simulations

Our MD simulations are implemented using the software package LAMMPS[15].The covalent carbon-carbon interactions are described by the second generation Brenner potential(REBO),which is widely used to study the graphite phase transition in previous studies[16,17].Note that the two cutoff distances are chosen as 1.7 and 1.92 ?,respectively,in order to avoid a non-physical strain hardening in the stress–strain behavior of carbon nanostructures owing to the discontinuity in the second derivative of the cutoff function[18].The cutoff function is taken to be 1.0 within a cutoff distance of 1.92 ? and zero otherwise[19].To obtain different chiral graphene sheets,the chiral angles are defined asα=arctan[31/2m/(2n+m)],wherenandmare integers in Fig.1a.Note that the atomic structures of chiral graphene sheets must meet periodic boundary conditions along both width and length directions.The(n,m)of(40,0),(47,5),(22,5),(30,11),(15,8),(19,14),and(23,23)graphene sheets with corresponding chiral anglesα=0.00°(zigzag),5.00°,10.02°,15.02°,20.03°,25.00°,and 30.00°(armchair)are investigated in this study,as shown in Fig.1b–f(because the shear properties of zigzag and armchair graphene sheets were studied in previous studies[9,14],the atomic structures of zigzag and armchair graphene sheets are not illustrated in Fig.1).Each initial structure is optimized and then is run for 5 ns at different temperatures until the pressure and energy of the system are stable,respectively,keeping both the given temperature and the pressureP=1 atm(the time stepΔt=1 fs),in the NPT ensemble controlled by the Nose-Hoovers thermostat[20,21].After the process and then keeping the structures in the NVT ensemble for 1 ns,the mechanical properties are calculated under shear deformation in the NVT ensemble.To obtain the reliable MD results and save the computational cost,we set the strain rate at 1×10?6/fs under shear deformation,in which such strain rate has been also validated for other materials(such as carbon nanotubes[22],graphene[16],and MoS2[23]).Periodic boundary conditions are applied in all three directions,where the vacuum size of 4 nm is perpendicular to each chiral graphene sheet so that the effect of van der Waals(vdW)force on the out-of-plane deformation of the graphene sheet can be neglected.

Fig.2 The loading direction-dependent shear stress–strain curves,buckling strains,and failure strains of different chiral graphene sheets.a The definition of the positive and negative shear deformation.b The loading direction-dependent shear stress–strain curves.c The loading direction dependent buckling strains and failure strains.d The chirality-dependent shear moduli and Poisson’s ratios

3 Results and discussion

To understand the loading direction-dependent shear behaviorof chiral graphene sheets, the definition of the positive and negative loading directions is shown in Fig.2a.Figure 2b shows the loading direction-dependent shear stress–strain curves of single-layer chiral graphene sheets at temperatureT=1 K.The stress–strain curves strongly depend on the loading direction because of the structural asymmetry except for zigzag and armchair graphene sheets.To quantitatively analyze the MD results,Fig.2c shows the buckling and failure strains of different chiral graphene sheets under different shear loading directions.The buckling and failure strains(solid boxes and circles in Fig.2c,respectively)under positive shear deformation are always higher than those under negative shear deformation(hollow boxes and circles in Fig.2c,respectively).The maximum values of the critical buckling shear strain and failure strain along the positive direction can be around 1.4 times higher than that along the negative loading direction.From elastic thin plate theory[24],the buckling stress under shear deformation can expressed as

whereKis the shape factor,bandhare the width and height of the rectangle plate,is the bending stiffness of the plate,tandμare the thickness and the Poisson’s ratio of the plate,respectively.Therefore,the buckling strain can be obtained

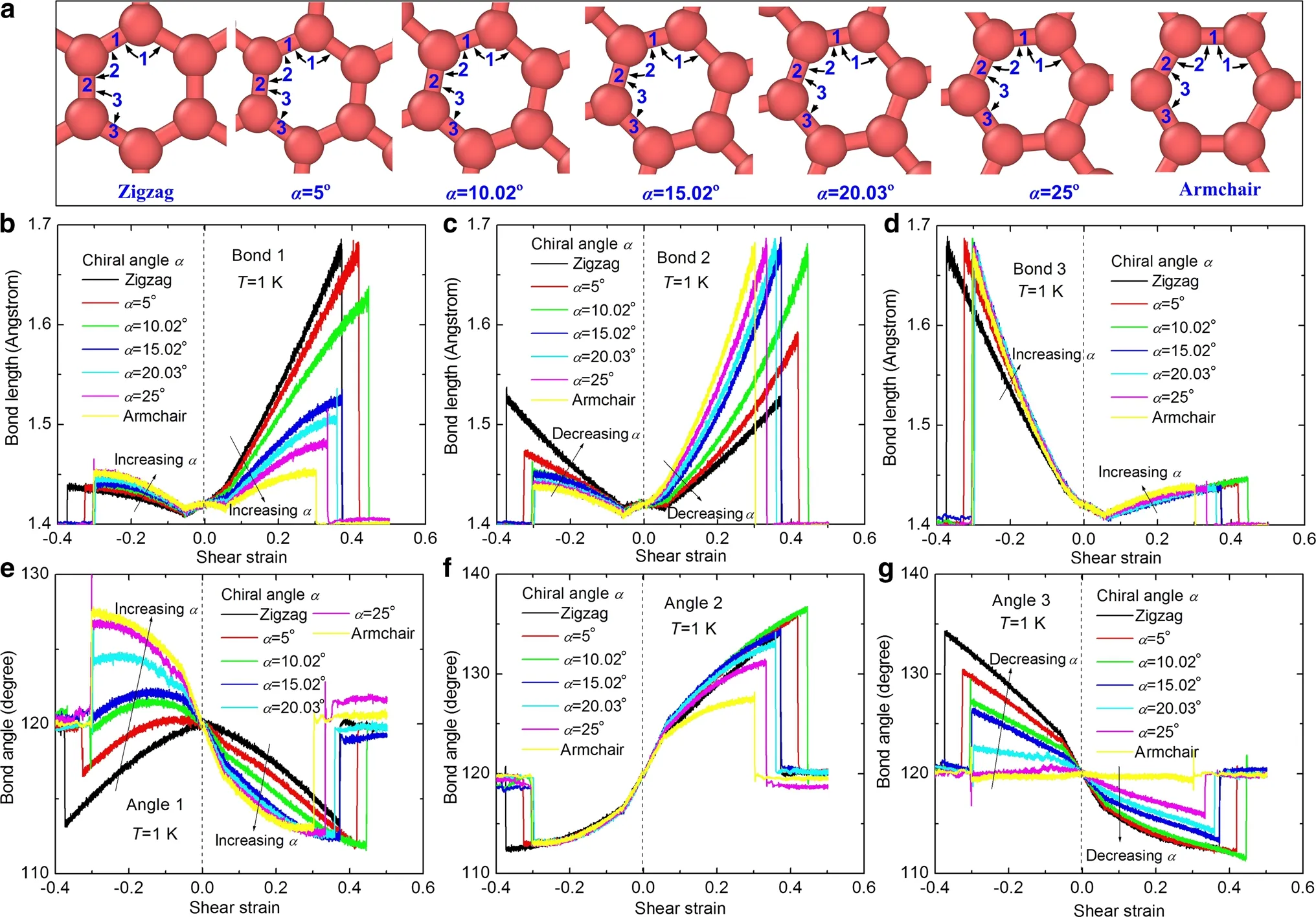
Fig.3 The distribution of three types of bonds and angles for different chiral graphene sheets under shear deformation.a The definition of three kinds of bonds and angles.b Bond 1.c Bond 2.d Bond 3.e Angle 1.f Angle 2.g Angle 3

The buckling strain is equal to 5.76%whent=3.4 ?,b=h=60 ?,K=9.16,andμ=0.16(see the dash line in Fig.2c)[19,24,25],which is very close to buckling strains of zigzag and armchair graphene sheets.On the other hand,the present failure strains of different chiral graphene sheets are from 30%to 44%,which are in good agreement with those(26%–45%)of previous studies[19,25].

Figure 2d shows the loading direction-dependent shear moduli and Poisson’s ratios of different chiral graphene sheets.The shear moduli of different chiral graphene sheets are from 310 to 320GPa by fitting the stress–strain curves at the shear strain?1%≤ε≤1%,which also agree well with those(260–460GPa)of previous literature[19,25].The present Poisson’s ratios in Fig.2dare from 0.11 to0.13by fitting the tensile strain–lateral strain curves at the tensile strainε≤0.1%(the detailed method can be seen in previous study[26]),which are a little smaller thanμ=0.16 in previous studies[19,25].

To reveal further the loading direction-dependent mechanism of the shear behavior for different chiral graphene sheets,the distribution of three types of bonds and angles is illustrated in Fig.3.Since the other three bonds in the hexagonal lattice are parallel to the present chosen three bonds,the change tendency of the two parallel bonds should be similar under shear deformation.Figure 3a shows the definition of three types of bonds and angles,where the hexagonal lattice rotates with chiral angle.Figure 3b,c shows that the lengths of both bond 1 and bond 2 under positive shear deformation increase more sharply than those under negative shear deformation,while the opposite trend is presented for bond 3 in Fig.3d.Therefore,the potential energy under positive shear deformation should be higher than that under negative shear deformation for a given shear strain.The failure stress(the maximum stress)under positive deformation should be also higher than that under negative deformation,which results in the larger failure strain under positive deformation.On the other hand,both bond 1 and bond 2 are mainly compressed under negative shear deformation while they are mainly stretched under positive shear deformation at small strains(see Fig.3b,c).Buckling under compression occurs more easily than that under tension,which leads to the higher buckling strain under positive deformation.Figure 3e,g shows that both angle 1 and angle 3 under positive shear deformation decreases with increasing shear strain,while the change of the angle 1 under negative shear deformation is quite different.The angle 1 of zigzag graphene sheets decreases and the angle 1of armchair graphene sheets andα=25°increases with increasing shear strain,while the angle 1 of the other chiral angles increases at first and then decreases with increasing shear strain.Furthermore,the angle 2 under positive shear deformation increases,while under negative shear deformation it decreases with increasing shear strain.In fact,the potential energy always increases no matter whether the bond angle increases or decreases.Therefore,the tendency of the three angles under different shear deformations also reveals that the potential energy under positive shear deformation is higher than that under negative shear deformation for a given shear strain,which results in the larger failure strain under positive deformation.From pre-vious study,the change of bond lengths dominates the total potential energy while the change of bond angles is the higher order terms of the total potential energy[26],so the change of bond lengths of Fig.3b–d can be used to reveal the loading direction-dependent mechanism of the shear behavior for different chiral graphene sheets.

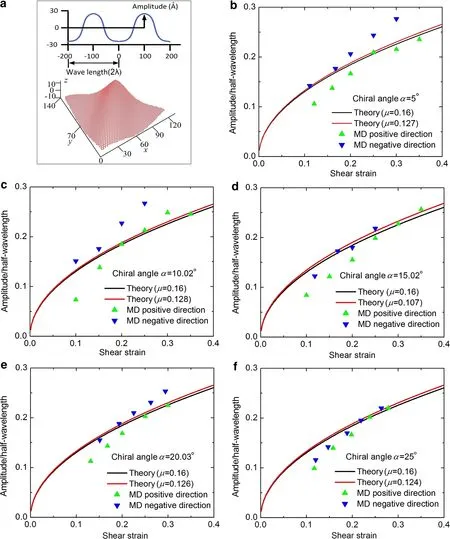
Fig.4 Ratio of amplitude to half-wavelength vs shear strain under different loading shear deformations for different chiral graphene sheets by MD simulations(T=1 K)and a theoretical method.a The schematic illustration of wrinkles and the wrinkles in a chiral graphene sheet(α =5°)at a shear strain of 0.2.b Chiral angle α =5°.c Chiral angle α =10.02°.d Chiral angle α =15.02°.e Chiral angle α =20.03°.f Chiral angle α=25°

Fig.5 Temperature-dependent failure strains and failure stresses for different chiral graphene sheets under positive and negative shear deformation.a Temperature-dependent failure strains.b Temperature-dependent failure stresses

Since wrinkles cause the softening of materials,the wrinkles play a key role in mechanical behavior of two dimensional materials.Graphene can be taken as a thin membrane structure,and its out-of-plane bending stiffness is quite low[27],so it is significant and necessary to understand its wrinkling behavior under shear deformation.To understand the effect of the wrinkles on the shear behavior of chiral graphene sheets,we study the grow th of wrinkles(the amplitudeωand wavelengthλ)of chiral graphene sheets under different shear directions in Fig.4.The ratio of the amplitude to the wavelength of wrinkles atT=1 K can be calculated directly from the MD results.The ratio from the available theory[28]can be expressed as

whereωis the amplitude,λis the wavelength,vis Poisson’s ratio,andγis the shear strain.Figure 4 shows the ratio of amplitude to half-wavelength vs.shear strain under different shear direction for different chiral graphene sheets by MD simulations and a theoretical method.Poisson’s ratios in Fig.4b–fare obtained from ourMD simulations(seeFig.2d)except forμ=0.16(μ=0.16 is used from previous work[22]).One can find that the effect of loading directions on the wrinkling is not remarkable.The present MD results are in reasonable agreement with those from the theoretical model.

To understand further the temperature effect on the shear behavior of chiral graphene sheets under different shear directions,Fig.5 shows the failure strains and failure stresses of chiral graphene sheets under different shear directions at different temperatures(fromT=100 K toT=900 K),where all solid configurations and hollow configurations are under positive shear deformation and negative shear deformation,respectively.Both failure strains and failure stresses at different temperatures under positive shear deformation are always higher than those under negative shear deformation except for the symmetric zigzag and armchair graphene sheets.For a given chiral angleα,both failure strains and failure stresses decrease with increasing temperature.The maximum values of both the failure strain and the failure stress under positive shear deformation is around 1.5 times higher than those under negative shear deformation at different temperatures.

4 Conclusion

In this study,the loading direction-dependent shear behavior of single-layer chiral graphene sheets at different temperatures has been obtained by MD simulations.The presentMD results show that the shear properties(such as shear stress–strain curves,buckling strains and failure strains)of chiral graphene sheets strongly depend on the loading direction due to the structural asymmetry.The maximum values of both the critical buckling strain and the failure strain under positive loading direction is around 1.4 times higher than those under negative loading direction.The loading direction-dependent mechanism of the shear behavior for different chiral graphene sheets has been revealed by analyzing the change of three kinds of bonds and angles.Both failure strain and failure stress decrease with increasing temperature,in which they under positive loading direction arealway shigher than those under negative loading direction for chiral graphene sheets.In particular,the amplitude to wavelength ratio of wrinkles for different chiral graphene sheets under shear deformation using MD simulations is in good agreement with that from the existing theory.Our findings are useful for understanding the shear behavior of chiral graphene sheets and their potential applications in nanodevices.

AcknowledgementsWe gratefully acknowledge the support from the National Natural Science Foundation of China(Grant 11572140),the Programs of Innovation and Entrepreneurship of Jiangsu Province,Primary Research&Development Plan of Jiangsu Province,Science and Technology Plan Project of Wuxi,the Fundamental Research Funds for the Central Universities(Grants JUSRP11529,JUSRP115A10,JG2015059),the research and practice project of teaching reform of graduate education in Jiangsu(Grant JGLX16_048),the Undergraduate Innovation Training Program of Jiangnan University of China(Grant 2015151Y),the Undergraduate Innovation and Entrepreneurship Training Program of China(Grant 201610295057),the Research Fund of State Key Laboratory of Mechanics and Control of Mechanical Structures(NUAA)(Grant MCMS-0416G01),the“Project of Jiangsu provincial Six Talent Peaks”in Jiangsu Province and “Thousand Youth Talents Plan.”

1.Wu,J.,Wei,Y.:Grain misorientation and grain-boundary rotation dependent mechanical properties in polycrystalline graphene.J.Mech.Phys.Solids 61,1421–1432(2013)

2.Chen,Y.,Zhang,Y.,Cai,K.,et al.:Interfacial thermal conductance in graphene/black phosphorus heterogeneous structures.Carbon 117,399–410(2017)

3.Eda,G.,Fanchini,G.,Chhowalla,M.:Large-area ultrathin films of reduced graphene oxide as a transparent and flexible electronic material.Nat.Nanotechnol.3,270–274(2008)

4.Lee,C.,Wei,X.,Kysar,J.W.,et al.:Measurement of the elastic properties and intrinsic strength of monolayer graphene.Science 321,385–388(2008)

5.Griffith,A.A.:The phenomena of rupture and flow in solids.Philos.Trans.R.Soc.Lond.A 221,163–198(1921)

6.Stankovich,S.,Dikin,D.A.:Graphene-based composite materials.Nature 442,282–286(2006)

7.Wu,S.,He,Q.,Tan,C.,et al.:Graphene—based electrochemical sensors.Small 9,1160–1172(2013)

8.Tan,X.,Wu,J.,Zhang,K.,et al.:Nanoindentation models and Young’s modulus of monolayer graphene:a molecular dynamics study.Appl.Phys.Lett.102,109(2013)

9.M in,K.,Aluru,N.R.:Mechanical properties of graphene under shear deformation.Appl.Phys.Lett.98,013113(2011)

10.Yeh,N.C.,Hsu,C.C.,Teague,M.L.,et al.:Nanoscale strain engineering of graphene and graphene-based devices.Acta Mech.Sin.32,497–509(2016)

11.Xu,X.,Rong,D.,Lim,C.W.,et al.:An analytical symplectic approach to the vibration analysis of orthotropic graphene sheets.Acta Mech.Sin.33,912–925(2017)

12.Nguyen,D.T.,Le,M.Q.,Bui,T.L.,et al.:Atomistic simulation of free transverse vibration of graphene,hexagonal SiC,and BN nanosheets.Acta Mech.Sin.33,132–147(2017)

13.Chang,T.:Torsional behavior of chiral single-walled carbon nanotubes is loading direction dependent.Appl.Phys.Lett.90,787(2007)

14.Yi,L.,Chang,T.:Loading direction dependent mechanical behavior of graphene under shear strain.Sci.China Phys.Mech.55,1083–1087(2012)

15.Plimpton,S.:Fast parallel algorithms for short-range molecular dynamics.J.Comput.Phys.117,1–19(1995)

16.Zhang,B.,Mei,L.,Xiao,H.:Nanofracture ingraphene under complex mechanical stresses.Appl.Phys.Lett.101,121915(2012)

17.Tabarraei,A.,Wang,X.,Jia,D.:Effects of hydrogen adsorption on the fracture properties of graphene.Comput.Mater.Sci.121,151–158(2016)

18.Belytschko,T.,Xiao,S.P.,Schatz,G.C.,et al.:Atomistic simulations of nanotube fracture.Phys.Rev.B 65,235430(2002)

19.Grantab,R.,Shenoy,V.B.,Ruoff,R.S.:Anomalous strength characteristics of tilt grain boundaries in graphene.Science330,946–948(2010)

20.Synder,R.G.,Schachtschneider,J.H.:A valence force field for saturated hydrocarbons.Spectrochim.Acta.21,169–195(1965)

21.Nosé,S.:A unified formulation of the constant temperature molecular dynamics methods.J.Chem.Phys.81,511–519(1984)

22.Wu,J.,Nagao,S.,He,J.,et al.:Nanohinge—induced plasticity of helical carbon nanotubes.Small 9,3561–3566(2013)

23.Zhao,J.,Kou,L.,Jiang,J.W.,et al.:Tension-induced phase transition of single-layer molybdenum disulphide(MoS2)at low temperatures.Nanotechnology 25,295701(2014)

24.Timoshenko,S.,Woinowsky-Krieger,S.:Theory of Plates and Shells.Engineering Societies Monographs,2ndedn.McGraw-Hill,New York(1959)

25.Pei,Q.X.,Zhang,Y.W.,Shenoy,V.B.:A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene.Carbon 48,898–904(2010)

26.Yang,Z.,Zhao,J.,Wei,N.:Temperature-dependent mechanical properties of monolayer black phosphorus by molecular dynamics simulations.Appl.Phys.Lett.107,023107(2015)

27.Gao,W.,Huang,R.:Thermomechanics of monolayer graphene:rippling,thermal expansion and elasticity.J.Mech.Phys.Solids 66,42–58(2014)

28.Wong,W.,Pellegrino,S.:Wrinkled membranes I:experiments.J.Mech.Mater.Struct.1,3–25(2006)