Yantao Yang·Junzhi Cui·Yifan Yu·Meizhen Xiang

1 Introduction

In classical solid mechanics and structural mechanics,the following dynamical equation is used for description of dynamical behavior of solid structures[1,2]:

whereui(x,t)denotes the displacement of the structure at positionxand timet,ρ(x)the mass density,Cijkl(x)the constitutive coefficient,andgi(x)the body force density.

However,in macroscopic dynamics of structures,any structural vibration system produces damping effects on the vibration due to factors like friction between devices and resistance from the environment.In vibration process the damping force does work to the system continuously,giving rise to energy loss of the system and continuing decrease of vibration amplitude,and the vibration will eventually tend to stop.To account for damping effects,a common method in structural dynamical analysis is to artificially introduce a damping term into the dynamical equation of the structure.

In general,damping force of vibration is relevant to vibration velocity.In structural dynamics,the most commonly used viscous damping model assumes that the damping force is proportional(but opposite in direction)to vibration velocity.With regard to the choice of damping coefficient,for multi-degree of freedom(MDOF)vibration system,the Rayleigh model is usually used in theory[3]:the damping coefficient matrix is chosen as the linear combination of mass and stiffness matrices.It is convenient for computation,but lacks theoretical basis.

Fig.1 Typical structure of polycrystalline atomic clusters(Source:“Microstructure of VT22(Ti5Al5Mo5V1,5Cr)after quenching”by Edward Pleshakov,used under the CC BY-SA 3.0 license)

It is worth noting that at micro–nano scales,damping effects are usually not considered in dynamical models for molecules and atoms.However,for a polycrystalline cluster structure shown in Fig.1,since it is comprised of numerous grains varying in size and orientation,the local vibration frequencies and modes of different grains differ substantially from each other.Therefore the local vibration of each grain is subjected to damping effects originated from the friction and van der Waals forces on interfaces exerted by neighboring grains.Thus,we reckon that the continuous dynamical equation for polycrystalline structure should include damping effects to describe the decaying phenomenon of each grain’s vibration.

The objective of this paper is to establish a continuous damping model for the structure with polycrystalline configuration demonstrated at micro–nano scales,and then derive the macroscopic continuous dynamical equation containing damping term.For this purpose,we first use the normal transformation to decompose the global motion of a crystal into the linear combination of single degree of freedom(SDOF)motion in normal directions(discrete modes),and then introduce damping force into each SDOF motion.Through interpolation of discrete modes,the continuous representation of crystal motion with damping effects can be obtained.From calculating energy loss on crystal interfaces,we derive the equation that damping coefficients satisfy,and obtain the relation of damping coefficients to average velocity of grain,roughness of interface,compressive stress at interface,and soon.Finally,we treat the polycrystalline cluster as a correlated multi-body contact system, introducing damping force into its equilibrium equation, and derive the homogenizeddynamical equation with damping term using two-scale homogenization method.

Before the formal discussion on continuous damping model for polycrystalline clusters,it is necessary to notice the difference between molecular dynamics(MD)model and continuum mechanics one.In MD model,structural deformation of discrete polycrystalline clusters and thermal vibration of molecules are merged and unified into the motion of atoms,whereas in continuum model,structural deformation,and thermal vibration are treated as two separate parts,and the change and migration of energy are also decomposed into “mechanical work”and “thermal migration”.Thus,when using the results of MD calculation to discuss dynamical behavior of polycrystalline clusters,it is necessary to decompose the kinematic positions of atoms.In fact,taking advantage of the profound difference in frequencies between structural deformation, and thermal vibration of polycrystalline clusters,the motion of atoms can be decomposed into two parts—structural deformation and thermal vibration:

Herexαandrepresent the instantaneous position and instantaneous velocity of atomα,respectively.and ˙ˉxαrepresent structural deformation position and velocity,respectively,corresponding to low frequency part ofandrepresent the displacement and velocity of atom due to thermal vibration,respectively,corresponding to high frequency part ofxα.

This paper focuses on dynamical behavior of polycrystalline clusters,therefore we shall ignore the thermal vibration part—and,and only consider the structural deformation part—and.Since the frequency of thermal vibration is substantially larger than that of structural deformation,in the process of MD simulation,we can take the time average of atomic position and velocity to eliminate the effects of thermal vibration.

The rest of this paper is structured as follows.Dynamical model for single crystal under unconstrained condition is discussed in Sect.2;dynamical model for polycrystalline clusters with damping effects is given in Sect.3;formulas for damping coefficients are derived by using conservation of energy in Sect.4;dynamical equilibrium equation with damping for grains is given in Sect.5;continuous dynamical equation with damping term for solid structures is given in Sect.6; finally,conclusions are drawn in Sect.7.

2 Dynamical model for single crystal

Assume that single crystal atomic clusterΩ0containsNatoms,with massm1,m2,...,mN,transient equilibrium positions,and current positionsx1,x2,...,xN.Hereˉxαandxα(α=1,2,...,N)can be written in coordinate component form asand(xα1,xα2,xα3)T,respectively.If we denote the displacements of atoms relative to equilibrium positions asu1,u2,...,uN,then

Displacements of atoms withinΩ0can be represented as a 3N-dimensional vectoru:

neglecting the higher order terms,the MD equation becomes

From Eqs.(22)and(23)we can observe thatφiis the normal mode of simple harmonic motion of single crystalΩ0;therefore we nameu=Φsasnormal transformation,siasnormal coordinate,andωiasnormal frequency.

From Eq.(17)we have

Therefore,ucan be decomposed as the linear combination of SDOF vibration in 3Ndirectionsφi.

It is worth noting that the normal frequencyωican be represented byM,K,φi:

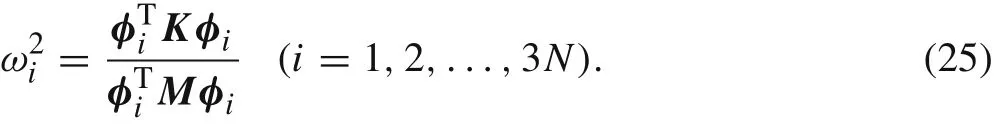
Now we substituteu=Φsinto the dynamical equation(15),and obtain

Multiplying the above equation on the left byΦTand noticing Eqs.(18)and(19),the motion equation ofΩ0becomes

The above is the simple harmonic motion equation of single crystalΩ0in discrete generalized modes under unconstrained and non-excited condition,it is similar in form to the simple harmonic oscillation.

Referring to Clough and Penzien[4],it is easy to obtain the solution of Eq.(28),here we omit it for simplicity.

3 Dam ping model for polycrystalline cluster motion

In polycrystalline clusters,because of the difference in size,shape,orientation,and structure of the grains,the difference in frequencies and modes of the grains are profound.Consequently,the free motion of each grain,especially those in the interior of the cluster,is subjected to damping and constraint on the interfaces of the grain,as shown in Fig.2.The damping and constraint originate from the friction and van der Waals force produced by the relative motion of atoms located on the interfaces.At this point,the SDOF motion equation(28)along single mode can no longer describe the motion behavior of grains in polycrystalline cluster correctly,therefore it is necessary to introduce reasonable damping term.

Fig.2 The motion of crystal grain is subjected to constraint from neighboring grains

Let us first consider the damping of SDOF motion along the modeφifor grainΩ0,the problem amounts to introducing damping term into Eq.(28).According to Clough and Penzien[4],the damping force is proportional to velocity,and can be expressed asThe damping coefficient of SDOF motion relies onand constraint behavior,and can be written as.

Thus,the SDOF Eq.(28)along the generalized discrete mode{φi},after introducing damping term,can be written as

whereC=diag(c1,c2,...,c3N).

Substitutings=Φ?1uinto the above equation,we obtain the motion equation ofΩ0with damping behavior in the original coordinates:

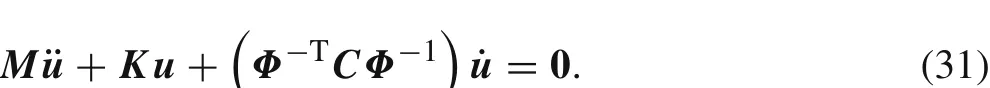
Using methods in the preceding section,we can first solve Eq.(29)to obtain the motionsi(t)in discrete modesφi,and then use Eq.(24)to obtain the global motionu(t)of the grain.Further,in order to obtain continuous displacement fieldu(x,t)on the grain,we need to continualize the discrete modesφi.

Sinceφiis a 3N-dimensional vector,it can be written as the combination ofN3-dimensional vectorsφiα(α=1,2,...,N),whose three components are corresponding to three coordinate directions,respectively:

It can be observed thatsiφiαrepresents the contribution to the motionuαof atomαfrom the motion along modeφi.

According to finite element interpolation,on the continuous domain thatΩ0occupies,we can construct a set of interpolation basis functionsNα(x)(α=1,2,...,N)based on the crystal lattices,such as BCC and FCC,which take the equilibrium positions of atomsˉxαas nodes,and satisfy

Thus,the continuous displacement fieldu(x,t)onΩ0can be decomposed as the linear combination of motion in 3Ncontinuous modesφi(x).Therefore,we can solve the equation of motion(29)onsi(t)in modeφito obtain the continuous displacement field onΩ0.

According to structural dynamics[4–6],the critical damping coefficient of the damping Eq.(29)along generalized vibration mode is,that is,under damping occurs whenci＜2?mωi.Define the damping ratio as

Substituting the expression ofsi(t)in to Eq.(37),we obtain the continuous displacement expression of the grainΩ0with damping effect:

It is easy to see thatu(x,t)→0 whent→+∞.

Next,we consider the influence of external loads on the motion in modeφi.If there exists external load termfor example,caused from the van der Waals force at interfaces(which we will discuss later),Eq.(29)becomes

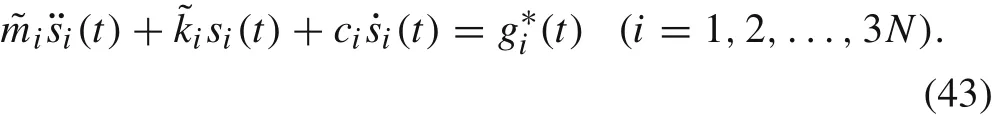
Suppose that a special solution of Eq.(43)isThen,according to theory of ordinary differential equations,the general solution of Eq.(43)can be expressed as the sum ofand the general solution of Eq.(29):

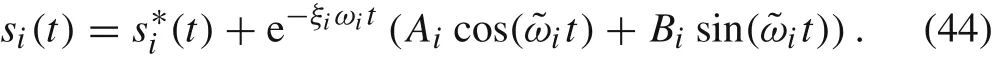
Substituting the above expression into Eq.(37),we obtain the expression of continuous displacement field of the grainΩ0with external loads:

4 Quantitative representation of dam ping coefficients

In order to calculate the magnitude of damping coefficient,we need to evaluate the loss of grain’s energy per unit time due to damping from both discrete and continuous perspectives,and derive the formula for damping coefficient using conservation of energy.

As discussed before,we first treat grainΩ0as a discrete system composed ofNatoms.According to Eqs.(22)and(23),the total energy ofΩ0is

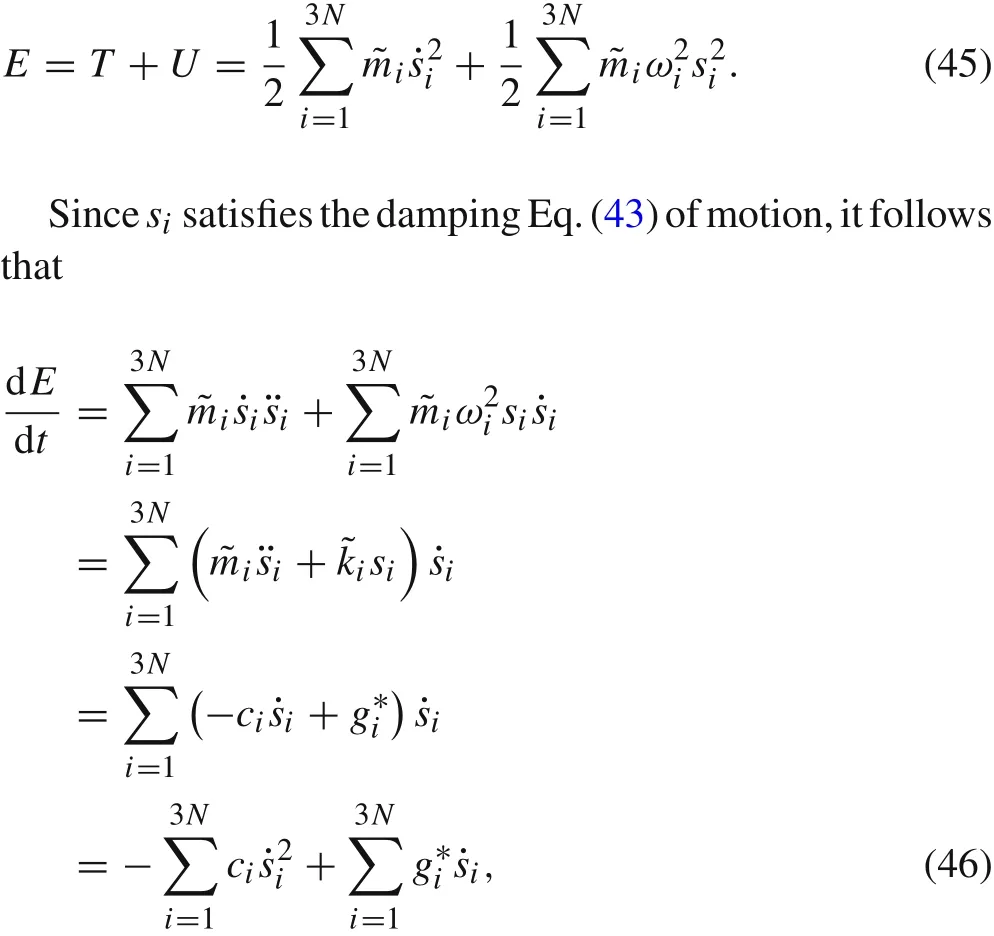
this is the change rate of the total energy of grainΩ0,or the change of total energy per unit time.

In our opinion,the change of total energy originates from friction force and van der Waals force on the interfaces.In Eq.(43),the damping termis produced by friction,the external load termis produced by van der Waals force.Therefore the first term in the right hand side of Eq.(46)represents the energy loss due to damping,while the second term represents the energy change due to external loads.

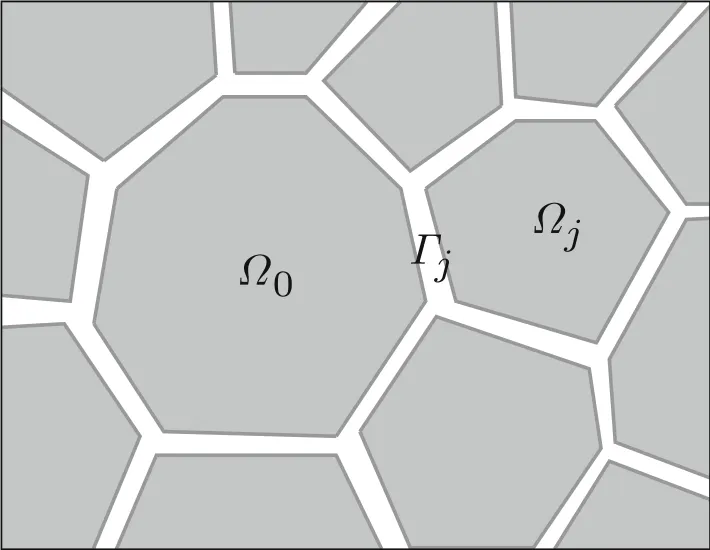
Fig.3 Interfaces between grains

Suppose that the grainΩ0hasJneighboring grainsΩ1,Ω2,...,ΩJ.As shown in Fig.3,we denote the interface betweenΩ0andΩjasΓj(j=1,2,...,J).

In order to calculate the damping force on the interfaces of grainΩ0and the work done by it,we need to treat the grain as a continuous body.Suppose that the surface stress ofΩ0atx∈Γjper unit area is.Denote the unit outer normal vector of?Ω0onΓjasnj,then the compressive stress atx∈Γjis

If,thenΩ0is subjected to compression byΩj,it leads to friction force that is proportional to compressive stress in magnitude,and opposite in direction to the relative motion of the two grains.The magnitude of friction force atx∈Γjper unit area can be written as

wherefjisthe friction coefficient on?Ω0∩Γjand is relative to the roughness and morphology of?Ω0.

If,thenΩ0is subjected to stretch on interfaceΓj,in this case there exists more complex friction mechanismwhich needs to be specially discussed, in this paper we simply suppose the friction force is 0.

Under both conditions,the magnitude of friction force can be written as

where the symbol(·)?denotes the negative part of the number inside the parentheses,and is formally defined as

Thus,the work done by friction force atxper unit area per unit time is

this is the equality that the damping coefficientsc1,c2,...,c3Nmust satisfy.

In order to quantitatively describe the damping coefficients,we assume that the 3Ndamping coefficients along 3Nmodesφi(i=1,2,...,3N)are approximately equal:then according to discussion in Sect.2we have1,2,...,3N),consequently the kinetic energy ofΩ0is

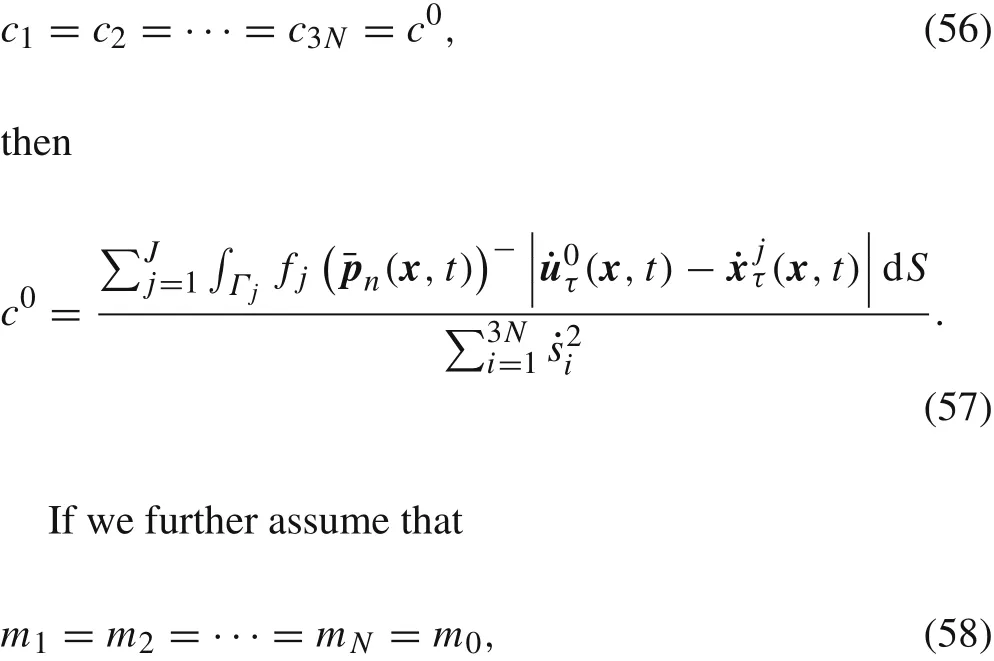
From the above expression we can observe that the damping coefficient decreases when the average speed of the grain increases,and increases when the roughness of interfaces and the compressive stress at interfaces increase.

Now we discuss approximate calculation method for the damping coefficientc0based on Eq.(62).

First of all,we consider the calculation of integral termin the numerator.

We can first calculate the stressatxusing the Atom ic–Continuum Coupled Model[7],and then use formula(47)to calculate the stress

The velocity termcan be obtained by interpolation of the velocities of atoms in the grainΩ0using expression(36).can also be obtained in similar way through interpolation of atoms inΩj.

In this way,we can obtain approximate value for the damping coefficientc0.

Further,suppose that the position of the centroid of grainΩjis atxj(j=0,1,...,J).Since the size of the grain is very small,can be approximated bywhereσ(x0,t)is the Cauchy stress atx0.Forwe have

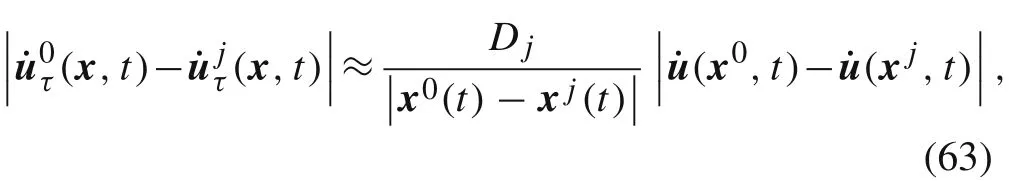
whereDjdenotes the thickness of the interfaceΓj.

In order to conveniently calculate the integrals on right side of formula(62),we approximately treatΩ0as a spherewith radiusR,whereRis the average of both radii of inscribed sphere and circumscribed sphere of grainΩ0,and represents the size ofΩ0.

Taking the first-order Taylor expansion of˙u(xj,t)atx0we have

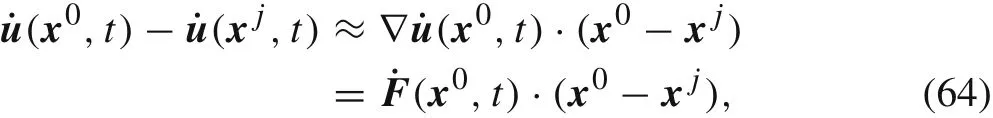
whereFdenotes the deformation gradient.

For the following derivation,we need to assume thatxj?x0is approximately in same direction tonj.This approximation becomes exact for polycrystalline structures generated by Voronoi tessellation,as we will use later.

After substituting Eq.(64)into Eq.(63),we have

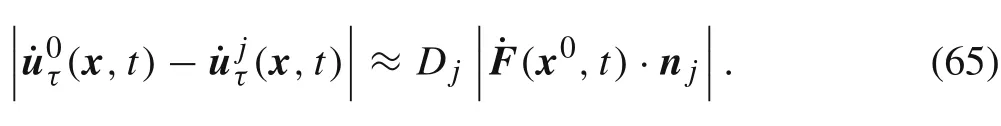
If we further assume that the friction coefficientfjand thicknessDjof all the interfacesΓj(j= 1,2,...,J)are approximately equal,then from Eq.(65)we obtain the approximate expression for damping coefficientc0:

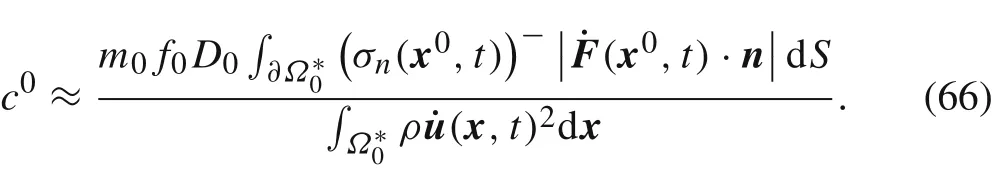
If the integrand in Eq.(66)is approximately taken as a constant,the expression ofc0can be further simplified.For the integral in the numerator we have

Fig.4 A polycrystalline Cu cluster sample(middle section)

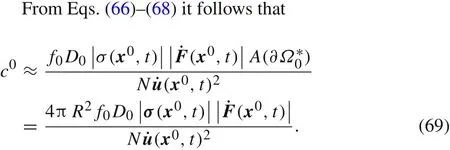
Now we make a brief remark on the expression(69).First of all,as discussed before,c0decreases when the average speed of the grain increases,and increases when the roughness of interfaces rises.The stress termin the numerator can be expressed from the constitutive relation:

whereaijkl(x0)is elastic constant,andεij(x0,t)is strain.Therefore,our damping model theoretically generalizes the Rayleigh’s model commonly used in engineering calculation,the damping coefficient relies on stiffness coefficient,roughness of interfaces,displacement velocity and the compactness of the materials,i.e.the thickness of grain’s interfaces.

Now,using the methods proposed above,we calculate the damping coefficient for a particular polycrystalline cluster sample,as shown in Fig.4,whose size is 108.45?×108.45?× 108.45?,and contains 105,384 atoms.The 54 grains of the cluster are generated by Voronoi tessellation[8,9],the orientation of each grain is random ly assigned.

The numerical experiment is taken at temperature of 300 K.Lammps[10]is used for MD simulation,the EAM many-body potential[11]is chosen to calculate the potential energy,the initial velocities of atoms are random ly assigned by the Gaussian distribution.The whole system is relaxed for 20 ps in the NVT ensemble[12,13],the average velocity and average stress of atoms over the last 2 ps are recorded.In the simulation results,the average speed and magnitude of average stress of the grains are shown in Figs.5and 6,respectively.

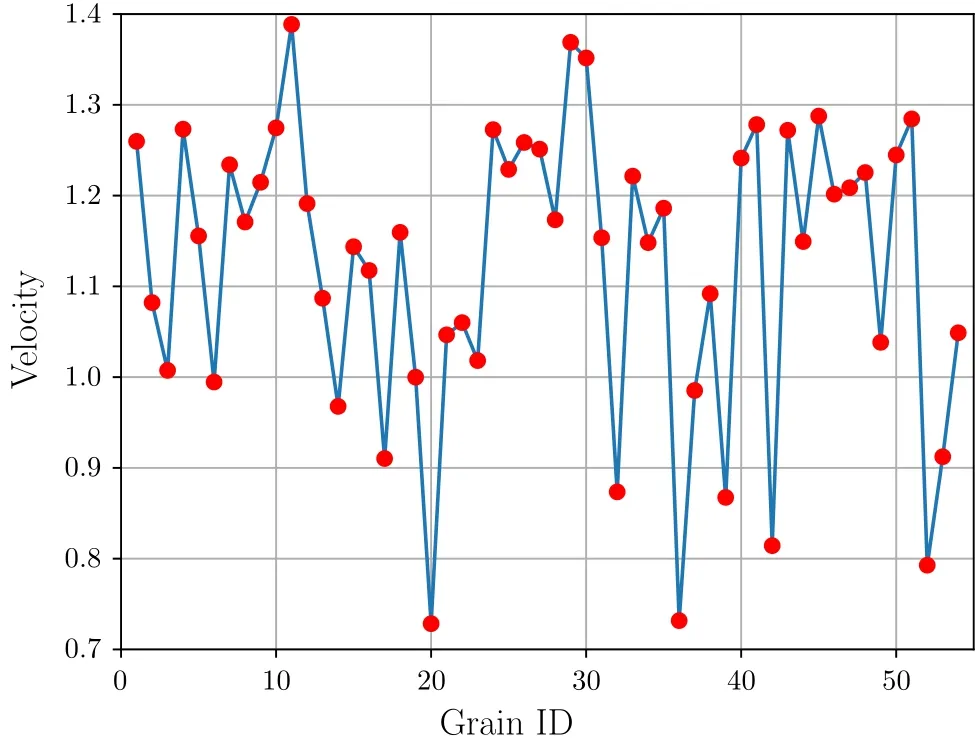
Fig.5 Distribution of speed after relaxation.The horizontal axis represents the Grain No.,ranging from 1 to 54;the vertical axis represents the average speed of the grain,in the unit of ? ·ps?1

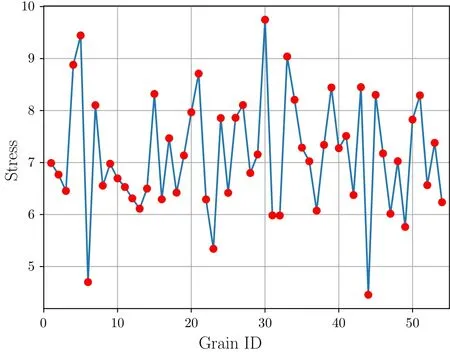
Fig.6 Distribution of stress after relaxation.The horizontal axis represents the grain No.,ranging from 1 to 54;the vertical axis represents the average stress of the grain,in the unit of GPa

By using the data of velocity field and stress field,damping coefficient of each grain in atomic dynamical equation sense can be calculated using Eq.(60),where the friction coefficient is chosen asfj=1.

The results of the damping coefficients are shown in Fig.7,and the numerical values are listed in Table 1.

The volume weighted average of the damping coefficients of all the grains isˉc=1.2207×10?14kg·s?1.

The above discussion is for the damping coefficient in the discrete dynamical equation of the grainΩ0.Below,we define the continuous damping coefficient.

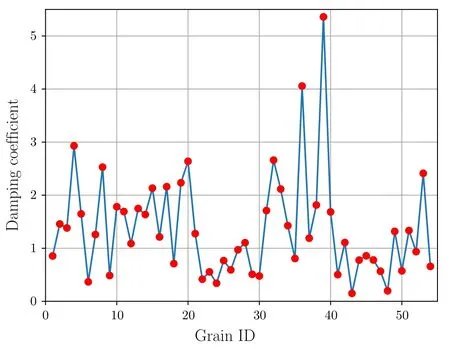
Fig.7 Damping coefficients of the polycrystalline Cu cluster sample.The horizontal axis represents the grain No.,ranging from 1 to 54;the vertical axis represents the damping coefficient of the grain,in the unit of 10?14 kg·s?1

Table 1 Damping coefficients of the polycrystalline Cu cluster

From the perspective of energy loss,the continuous damping coefficientc0ofΩ0and its discrete counterpartc0should satisfy

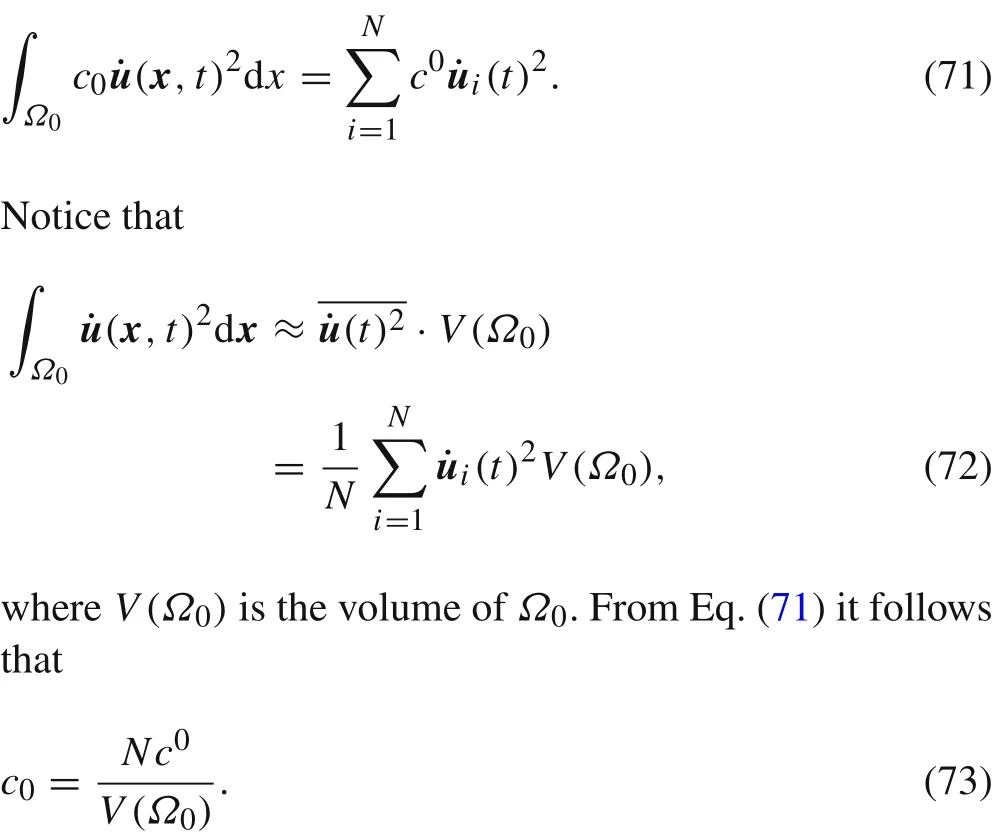
Thus,the expression(73)defines the continuous damping coefficient of the grainΩ0.Using it we can calculate thecontinuous damping coefficients of the grains of the polycrystalline Cu cluster sample above.The results are shown in Table 2.

Table 2 Continuous damping coefficients of the polycrystalline Cu cluster

5 The dynamical equilibrium equation with dam ping for grains

As we have discussed above,besides the damping force caused from crystal interfacesΓj(j=1,2,...,J),grainΩ0located inside polycrystalline cluster is also subjected to some exciting forces from neighboring grainsΩj(j=1,2,...,J),such as van der Waals force on the interfaceΓj.To investigate the equilibrium ofΩ0,we must consider all the forces produced by all the neighbouring grains.

According to Israelachvili[14],the van der Waals force on grain interfaceΓjper unit area can be approximately expressed as

whereρ0andρjare the mass density ofΩ0andΩj,respectively,Cis the van der Waals force coefficient between two atoms,and is related to element properties.Ajis usually at the scale of 10?19J[14].

Thus,the van der Waals force acted on atomαlocated onΓj??Ω0is

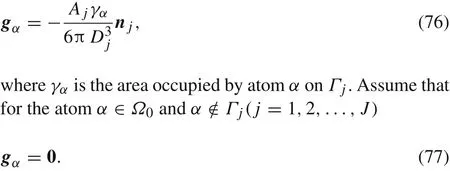
Let us define the 3N-dimensional discrete loading vector excited by van der Waals force onΓj(j=1,2,...,J)for grainΩ0as the combination ofgα:

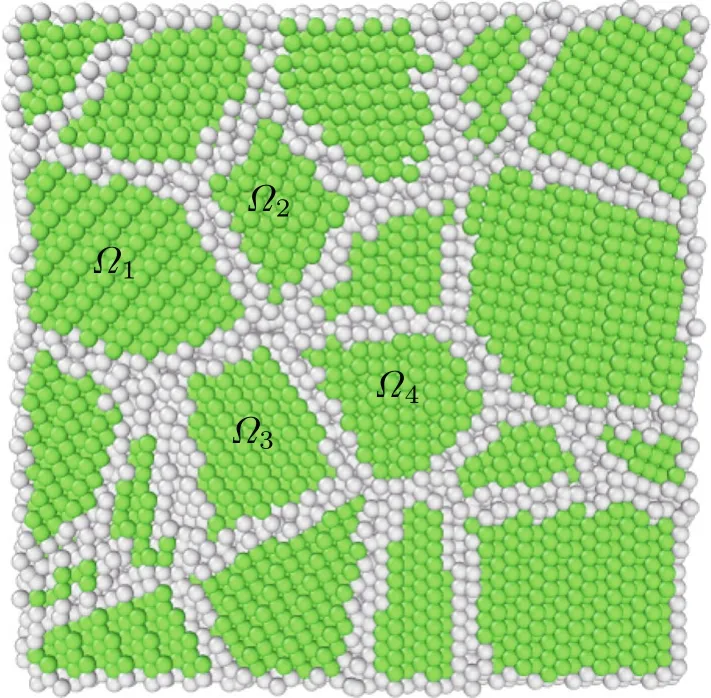
Fig.8 Reference cell Q

Similar to the definition Eq.(36)in Sect.3,from Eq.(78)we can obtain the 3-dimensional continuous representation of the discrete loading vector caused by van der Waals force as follows

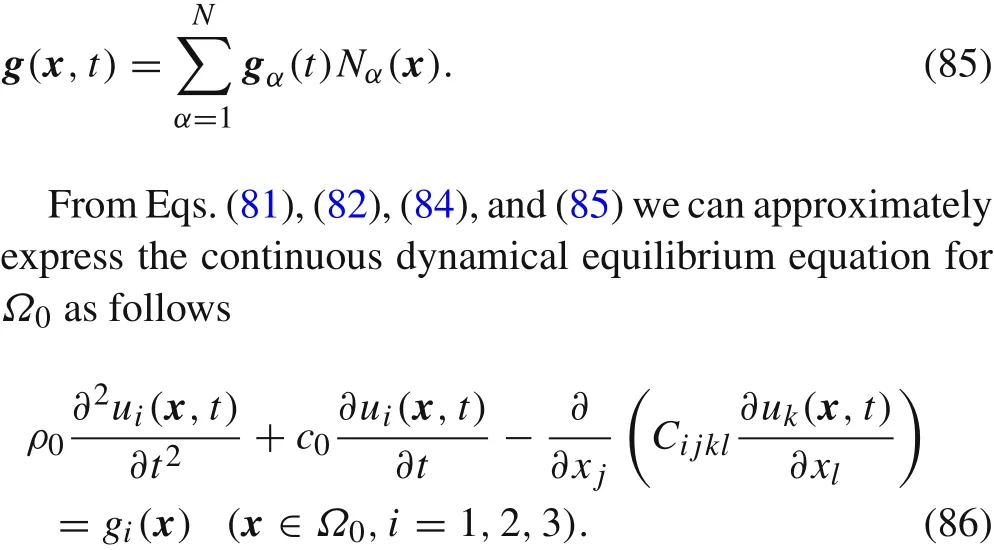
6 Continuous dynamical equation with dam ping term for solid structures

Suppose that a solid structureΩis composed of a series of polycrystalline cluster cellsεQat micro level:

whereQis 1-normalized cube shown in Fig.8,andεis unit cellular size.

The continuous dynamical equation with damping term for the solid structureΩwill be given by using two-scale homogenization method in this section.The discussion will be separated into two parts.The first part is for the case thatΩisε-periodic,which means all of the polycrystalline cluster cells have the same configuration.The second part is for the case of realistic configuration of solid materials that the configuration of each polycrystalline cluster cell is random,which means the configurations of polycrystalline cluster cells are different from each other due to the randomness.

6.1 Continuous dynamical equation with dam ping term for periodic configuration

Suppose that all of the polycrystalline clustersεQare same like that in Fig.8,which containsIgrainsΩ1,Ω2,...,ΩI.By using the formulation in Sect.5,andcan be calculated,and then we can construct the following functions on

this is the transform formula for elastic constant from the coordinate system of the grain to that of the reference cellQ.

For the polycrystalline Cu cluster sample composed of 54 grains in Sect.4,the homogenized mass density is calculated to be,the homogenized damping coefficient is.The homogenized elastic constants written in 6×6 matrix form are

the numbers are in the unit of GPa.

6.2 Continuous dynamical equation with dam ping term for realistic solid structure

Below,we suppose thatΩis composed of cellsεQwith independently randomly distributed grains,that is,parameters of grains,such as size and orientation in each cell,obey the same probability distribution.And we also assume that each cell forms a Voronoi tessellation.

The probability distribution model of grains in each cell is the same,the wholeΩis generated by such cells.Therefore,once the probability distribution model of grains in one cell is determined,the structural feature of the wholeΩis determined.A Voronoi tessellation can be uniquely determined by the Voronoi points that generate this tessellation,hence the spatial configuration of grains can be generated by the coordinatexcof the Voronoi points.The orientation of a grain can be generated by two perpendicular vectorsα,βand their outer productα×β.Thus,let random vectorζ=(xc,α,β),which contains 9 random parameters,thenζcontains the complete information of a grain.

Suppose that the cellCsis composed ofIgrains,and then define the distribution sample of grains in the cell as

According to the above discussion,a solid structureΩwith randomly distributed grains can be seen at micro–nano scales as a set ofε-sized cellsε(Q+z),which obey the same probability distribution P:

By two-scale homogenization method[23,24]we obtain that the homogenized mass density,damping coefficient and elastic constant for a sampleωsare the following

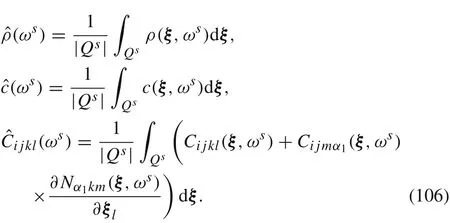
And then taking many samplesωs(s=1,2,...,n),and using Kolmogorov’s strong law of large numbers[25],we obtain that the expected homogenized coefficients are the following

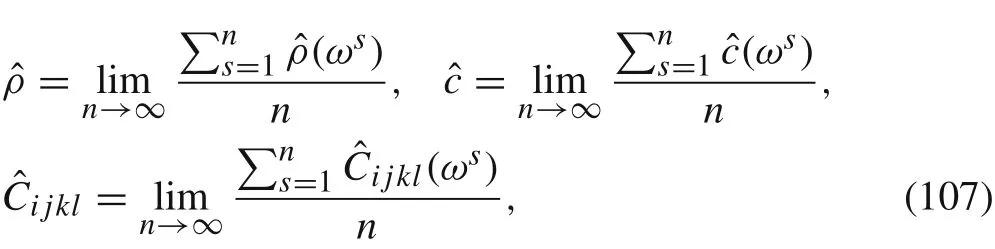
where?ρis called the effective mass density,?cthe effective damping coefficient,and{?Cijkl}the effective elasticity tensor.

Till now,we conclude that the macroscopic continuous dynamical problem with damping term is the following

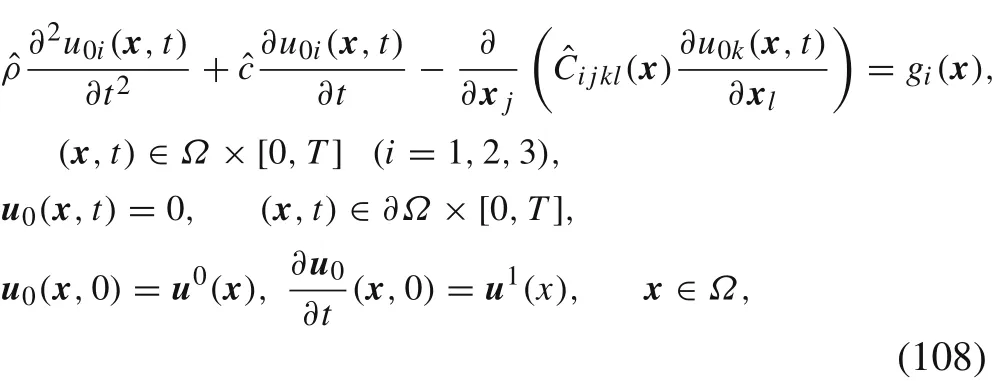
whereu0(x,t)is the macroscopic continuous solution.

7 Conclusions

For polycrystalline clusters at micro–nano scale,we introduced damping force into the motion equation along each discrete mode of grain motion,and then by interpolation of the discrete modes,we obtained the continuous expression of the global motion of grain including damping effects.Using conservation of energy we derived the expression of damping coefficients.Based on that we gave the approximate method for calculating damping coefficients.For a randomly generated polycrystalline Cusample,we implemented the numerical calculation of damping coefficients.Furthermore,we treated the polycrystalline cluster as a correlated multi-body contact system,introducing damping force into the equilibrium equation of the polycrystalline cluster,and then obtained the continuous dynamical equation containing damping term.Finally,using two-scale homogenization method,we gave the macroscopic continuous dynamical problem with damping effects.

From the discussion in previous sections we also concludethat the damping coefficient of a solid structure does not onlydepend on the mesoscopic and microscopic configurations of materials,including the shapes and size of grains,the morphology features and thickness of the internal interfaces,and cavities inside,but also on its motion status,such as motion velocity and the rate of deformation gradients.Thus,in the strict sense,the dynamical problem with damping effect for solid structure is a complex nonlinear problem.

AcknowledgementsThis work was partially supported by the National Basic Research Program of China(973Program Grant2012CB025904),the National Natural Science Foundation of China(Grant 11102221),and the State Key Laboratory of Science and Engineering Computing(LSEC).

1.Bower,A.F.:Applied Mechanics of Solids.CRC Press,Boca Raton(2009)

2.Tadmor,E.B.,Miller,R.E.:Modeling Materials.Continuum,Atomistic and Multiscale Techniques.Cambridge University Press,Cambridge(2011)

3.Wilson,E.L.:Three Dimensional Static and Dynamic Analysis of Structures.Computers and Structures Inc,Berkeley(2000)

4.Clough,R.W.,Penzien,J.:Dynamics of Structures.McGraw-Hill College,New York(1975)

5.Chopra,A.K.:Dynamics of Structures.Pearson,Upper Saddle River(2016)

6.Williams,M.:Structural Dynamics.CRC Press,Boca Raton(2016)

7.Li,B.,Cui,J.,Tian,X.,et al.:The calculation of mechanical behavior for metallic devices at nano-scale based on Atomic–Continuum Coupled model.Comput.Mater.Sci.94,73–84(2014)

8.Aurenhammer,F.,Klein,R.,Lee,D.T.:Voronoi Diagrams and Delaunay Triangulations.World Scientific Publishing Co Inc,Singapore(2013)

9.Okabe,A.,Boots,B.,Sugihara,K.,et al.:Spatial Tessellations.Concepts and Applications of Voronoi Diagrams.Wiley,New York(2009)

10.Plimpton,S.:Fast parallel algorithms for short-range molecular dynamics.J.Comput.Phys.117,1–19(1995)

11.Foiles,S.M.,Baskes,M.I.,Daw,M.S.:Embedded-atom-method functions for the fccmetalsCu,Ag,Au,Ni,Pd,Pt,and theiralloys.Phys.Rev.B 33,7983–7991(1986)

12.Thijssen,J.:Computational Physics.Cambridge University Press,Cambridge(2007)

13.Frenkel,D.,Sm it,B.:Understanding Molecular Simulation.From Algorithms to Applications.Academic Press,San Diego(2001)

14.Israelachvili,J.N.:Intermolecular and Surface Forces.Academic Press,San Diego(2015)

15.Xiang,M.,Cui,J.,Li,B.,et al.:Atom-continuum coupled model for thermo-mechanical behavior of materials in micro–nano scales.Sci.China Phys.Mech.Astron.55,1125–1137(2012)

16.Han,T.,Cui,J.,Yu,X.,et al.:A local Quantum–Atomistic–Continuum model for mechanical behaviors at micro–nano scale.Comput.Mater.Sci.109,312–322(2015)

17.Yang,Y.,Cui,J.,Han,T.:Error analysis for momentum conservation in Atom ic–Continuum Coupled Model.Comput.Mech.58,199–211(2016)

18.Han,T.:A local Quantum–Atomistic–Continuum model for mechanical behaviors of micro–nano materials and components.[Ph.D.Thesis],University of Chinese Academy of Sciences,China(2016)

19.Cioranescu,D.,Donato,P.:An Introduction to Homogenization.Oxford University Press,Oxford(1999)

20.Pavliotis,G.A.,Stuart,A.:Multiscale Methods.Averaging and Homogenization.Springer,New York(2008)

21.Wan,J.:Multi-scale analysis method for dynamic coupled thermoelasticity of composite structures.[Ph.D.Thesis],University of Chinese Academy of Sciences,China(2007)

22.Grinfeld,P.:Introduction to Tensor Analysis and the Calculus of Moving Surfaces.Springer,New York(2013)

23.Yang,Z.:The second-order two-scale method for predicting dynamic thermo-mechanical performance of random composite materials.[Ph.D.Thesis],Northwestern Polytechnical University,China(2014)

24.Yang,Z.,Cui,J.:The statistical second-order two-scale analysis for dynamic thermo-mechanical performances of the composite structure with consistent random distribution of particles.Comput.Mater.Sci.69,359–373(2013)

25.Ross,S.:A First Course in Probability.Pearson,Upper Saddle River(2015)