素超代數(shù)的廣義超導(dǎo)子和局部廣義超導(dǎo)子
袁鶴
(吉林師范大學(xué)數(shù)學(xué)學(xué)院,吉林四平 136000)
1 引言
設(shè)A是代數(shù),若A上的線性映射d滿足對(duì)于任意a∈A存在導(dǎo)子da:A→A使得d(a)=da(a),則稱d是A上的局部導(dǎo)子.Kadison[1]與Larson和Sourour[2]最先開(kāi)始研究局部導(dǎo)子,他們得到一些特殊的代數(shù)上的局部導(dǎo)子是導(dǎo)子.Bre?ar[3]證明了含有非平凡冪等元的素環(huán)上的局部導(dǎo)子是導(dǎo)子.Fo?ner[4]將Bre?ar[3]的結(jié)果推廣到了超代數(shù)上.1991年,Bre?ar[5]給出了環(huán)上廣義導(dǎo)子的定義:若對(duì)于環(huán)R上的加法映射g存在R上導(dǎo)子d滿足g(xy)=g(x)y+xd(y),x,y∈R,則稱g是R上的廣義導(dǎo)子.王宇[6]研究了含有非平凡冪等元的素環(huán)上的Bre?ar意義下的局部廣義導(dǎo)子.2015年,趙延霞等[7]研究了可換環(huán)上上三角矩陣?yán)畲鷶?shù)的局部自同構(gòu)和局部導(dǎo)子.
Nakajima在文獻(xiàn)[8]中還引入了另一種廣義導(dǎo)子.設(shè)A是代數(shù),m∈A,g:A→A是線性映射,如果
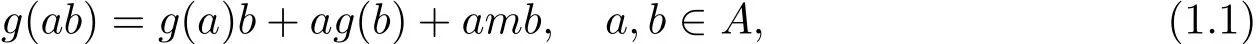
則稱(g,m)是A上的廣義導(dǎo)子.特別地,若A含有單位元1,則m=?g(1).Fo?ner[9]研究了由冪等元生成的代數(shù)上的Nakajima意義下的局部廣義(α,β)-導(dǎo)子.
根據(jù)Nakajima意義下的廣義導(dǎo)子的定義,我們給出了廣義超導(dǎo)子和局部廣義超導(dǎo)子的定義.證明了具有非平凡冪等元的素超代數(shù)上的局部廣義超導(dǎo)子均為廣義超導(dǎo)子,還給出了廣義超導(dǎo)子的一個(gè)刻畫(huà).

定義1.1設(shè)A是超代數(shù)且i∈{0,1}.若m∈Ai與i階線性映射g:A→A滿足
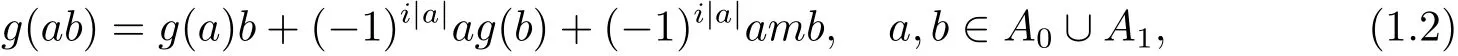
則稱(g,m)是A上i階的廣義超導(dǎo)子.一個(gè)0階廣義超導(dǎo)子與一個(gè)1階廣義超導(dǎo)子之和稱為A上的廣義超導(dǎo)子.
若A含有單位元1,則上述定義中的m=?g(1).顯然,g(xy)=g(x0y0)+g(x0y1)+g(x1y0)+g(x1y1),其中x=x0+x1,y=y0+y1.根據(jù)環(huán)上Bre?ar意義下的廣義導(dǎo)子的定義,本文作者[10]給出了超代數(shù)上Bre?ar意義下的廣義超導(dǎo)子的定義.
定義1.2設(shè)A是超代數(shù),g:A→A是i階線性映射,若存在A上i階的超導(dǎo)子d滿足
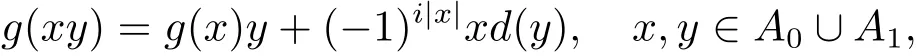
則稱g是A 上i階的Bre?ar型廣義超導(dǎo)子.若g=g0+g1,其中g(shù)i是A上i階的Bre?ar型廣義超導(dǎo)子,則稱g是A上的Bre?ar型廣義超導(dǎo)子,稱d=d0+d1是g的相伴超導(dǎo)子.
實(shí)際上,Nakajima型廣義超導(dǎo)子均為Bre?ar型廣義超導(dǎo)子.定義映射d=g+λa,其中λa(x)=mx,所以d(s)=g(s)+ms,s∈H(A).因此對(duì)于任意s,t∈H(A),
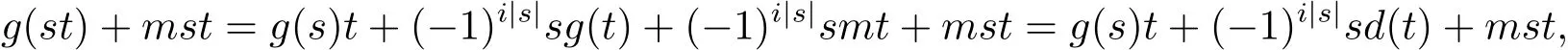
所以g(st)=g(s)t+(?1)i|s|sd(t).又因?yàn)?/p>

所以d是A上i階的超導(dǎo)子.
定義1.3設(shè)A是超代數(shù)且i∈{0,1}.若i階線性映射g:A→A滿足對(duì)于任意x∈A存在i階的廣義超導(dǎo)子(gx,m):A→A使得g(x)=gx(x),則稱g是A上i階的局部廣義超導(dǎo)子.一個(gè)0階局部廣義超導(dǎo)子與一個(gè)1階局部廣義超導(dǎo)子之和稱為A上的局部廣義超導(dǎo)子.
設(shè)A=A0⊕A1是超代數(shù),定義集合E=E0⊕E1,其中E0={e∈A0|e2=e}(E0是A0中所有冪等元構(gòu)成的集合),E1={e∈A1|存在e′∈E0滿足(e′+e)2=e′+e}.因?yàn)?e′+e)2=e′+e,e′∈ E0,e ∈ E1,所以 e2=0,e′e+ee′=e.用 R=R0⊕R1來(lái)表示由 E 生成的A 的子超代數(shù),用I=I0⊕I1來(lái)表示由[E0,A]生成的A 的分次理想,其中[·,·]表示換位子.由文獻(xiàn)[4,引理1.2],I?R.如無(wú)特殊說(shuō)明,本文中的A是指含有單位元和非平凡冪等元的素超代數(shù).顯然,I0.對(duì)于A的元素,我們將用帶下標(biāo)的同一字母表示該元素的齊次分量,例如若x∈A,則其0次和1次齊次分量分別記作x0和x1.
2 局部廣義超導(dǎo)子
本節(jié)將證明A上的局部廣義超導(dǎo)子是廣義超導(dǎo)子.
引理2.1設(shè)g是A上i階的局部廣義超導(dǎo)子,則
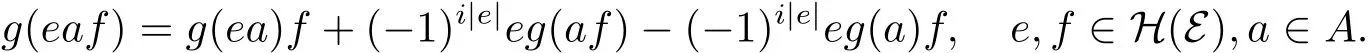
證因?yàn)間是A上i階的局部廣義超導(dǎo)子,i∈{0,1},所以對(duì)于任意y∈A,x∈H(A),z∈A,存在i階的廣義超導(dǎo)子(gy,m)滿足
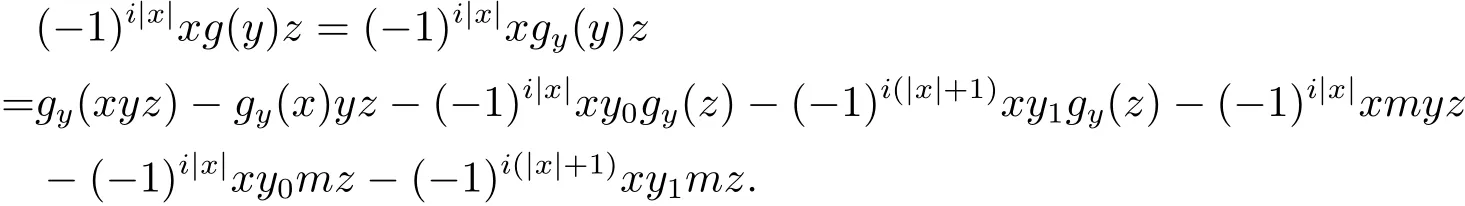
現(xiàn)在斷言,對(duì)于任意x,y∈A,若xy=yz=0,則必有(x0+(?1)ix1)g(y)z=0.實(shí)際上,由可得x0y0+x1y1=x0y1+x1y0=0,從而
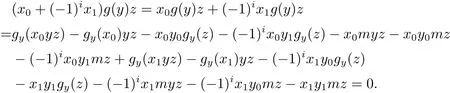
設(shè)e,f是A中的冪等元,則對(duì)于任意a∈A均有
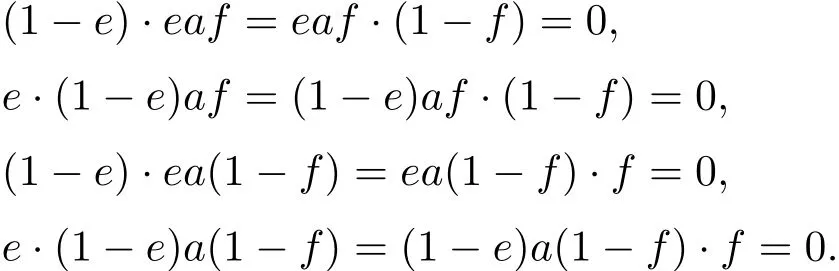
因此,對(duì)于e0∈E0,f0∈E0,根據(jù)上面的斷言可得
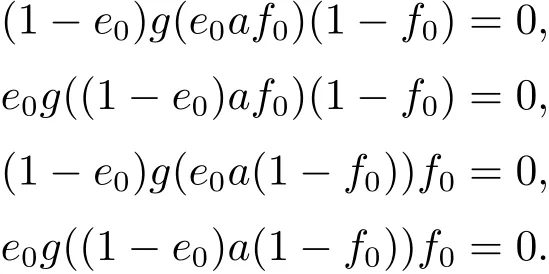
因此
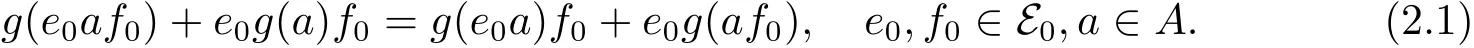
對(duì)于e0∈E0,f=f0+f1∈E,f0∈E0,f1∈E1,再由上面的斷言可得
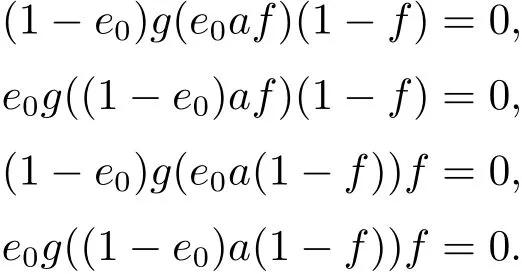
因此
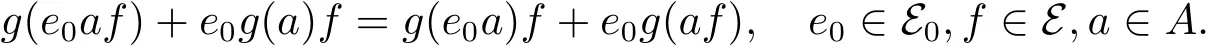
再由(2.1)式有
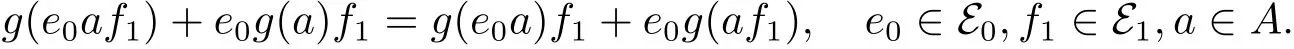
類似地,對(duì)于任意f0∈E0,e1,f1∈E1,a∈A,有

因此g滿足
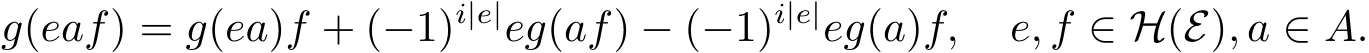
引理2.2設(shè)g是A上i階的局部廣義超導(dǎo)子,則
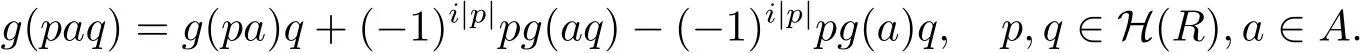
證只需證明對(duì)于任意e1,···,em,f1,···,fn∈ H(E)均有
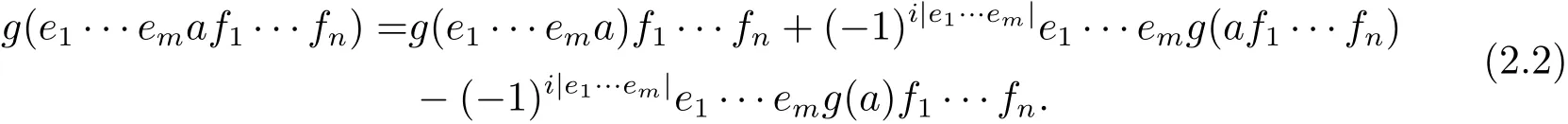
先假設(shè)m=1.現(xiàn)在對(duì)n用數(shù)學(xué)歸納法.顯然當(dāng)n=1時(shí),(2.2)式成立.假設(shè)(2.2)式對(duì)于n成立.那么
因此當(dāng)m=1時(shí),(2.2)式對(duì)于任意n都成立.下面對(duì)m用數(shù)學(xué)歸納法.已經(jīng)證明當(dāng)m=1時(shí),(2.2)式成立.現(xiàn)在假設(shè)(2.2)式對(duì)于m成立.那么因此(2.2)式對(duì)于任意m,n都成立.
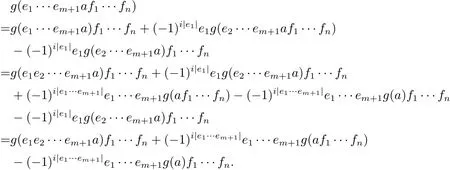
引理2.3設(shè)A是含有單位元和非平凡冪等元的素超代數(shù),若g是A上i階的局部廣義超導(dǎo)子,則(g,g(1))是A上i階的廣義超導(dǎo)子.
證在引理2.2中,取a=1有
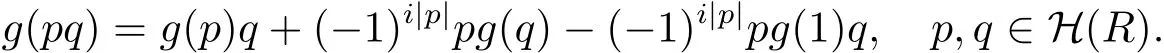
因?yàn)镮?R,所以

又因?yàn)?/p>
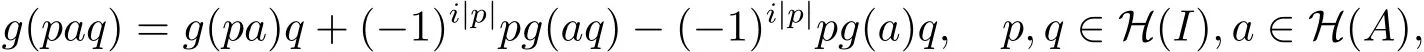
所以上面兩式相減有
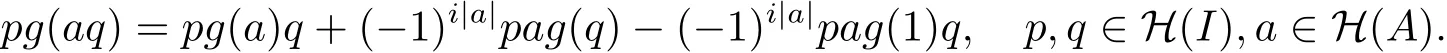
因?yàn)閜∈H(I),所以
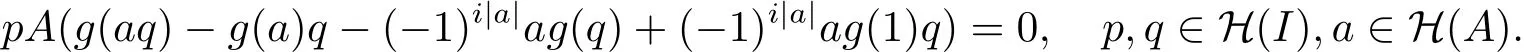
因?yàn)锳是素超代數(shù),所以
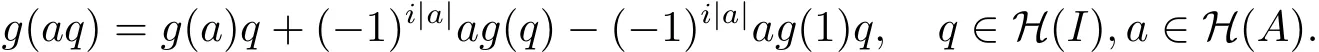
用兩種不同的方式展開(kāi)g(abq),對(duì)于任意q∈H(I),a,b∈H(A),有
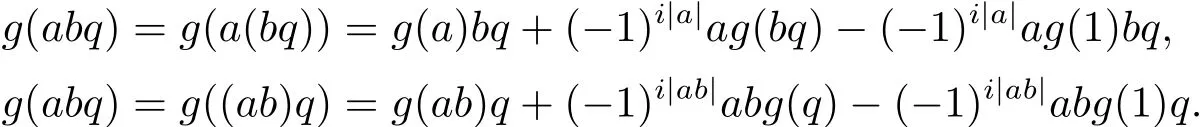
兩式相減有
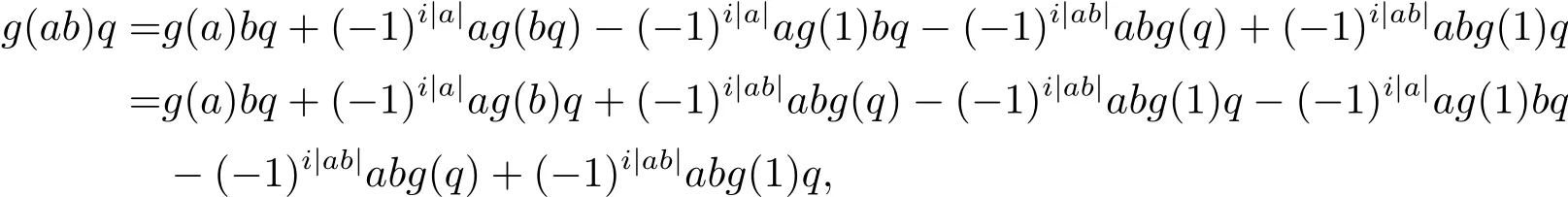
因此
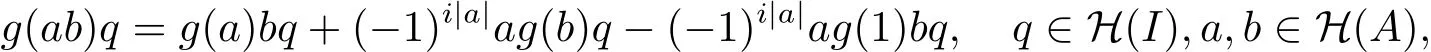
整理有

因?yàn)閝∈H(I),所以

因?yàn)锳是素超代數(shù),所以
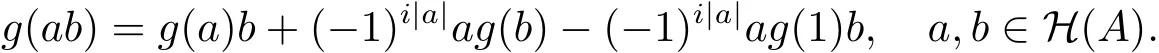
因此(g,g(1))是A上i階的廣義超導(dǎo)子.
由上面這個(gè)引理有
定理2.4設(shè)A是含有單位元和非平凡冪等元的素超代數(shù),A上的局部廣義超導(dǎo)子是廣義超導(dǎo)子.
3 廣義超導(dǎo)子
定理3.1設(shè)A是具有非平凡冪等元的素超代數(shù),g:A→A是i階線性映射,m∈Ai,則(g,m)是i階的廣義超導(dǎo)子的充分必要條件是對(duì)于任意的x,y∈A,當(dāng)xy=0時(shí),
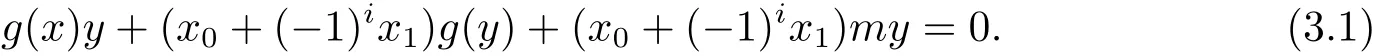
顯然,A上i階的廣義超導(dǎo)子滿足上式.本節(jié)主要是證明充分性.為了方便,設(shè)
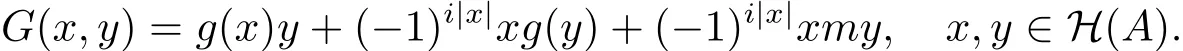
引理3.2G(xr,z)=G(x,rz), x,z∈H(A),r∈H(R).
證設(shè)e是A中的冪等元,任取x,z∈H(A),因?yàn)?/p>

所以對(duì)于e0∈E0,由(3.1)式可得
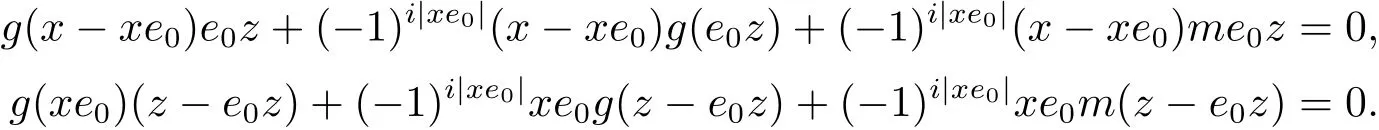
兩式相減有
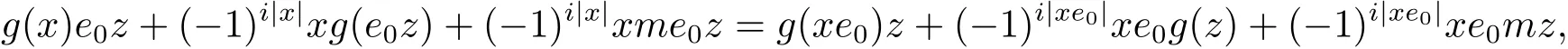
即G(x,e0z)=G(xe0,z).再由(3.1)式,對(duì)于任意x,z∈H(A),有
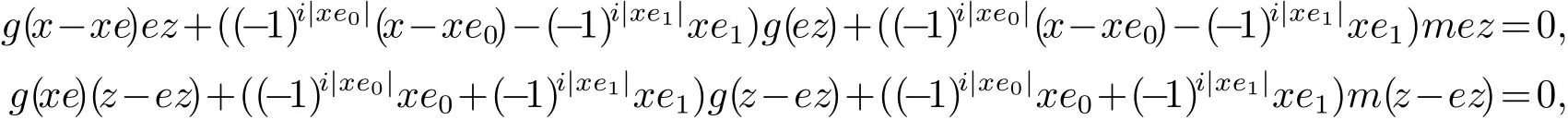
其中e=e0+e1.兩式相減有
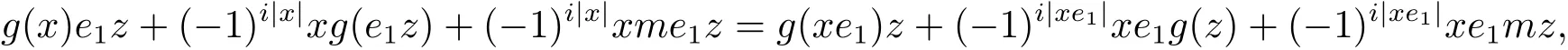
即G(x,e1z)=G(xe1,z).因此對(duì)于任意e∈H(E)有G(x,ez)=G(xe,z).設(shè)T={r∈H(A)|G(xr,z)=G(x,rz),x,z∈H(A)}.因?yàn)閷?duì)于任意r,r′∈T,x,z∈H(A),有

所以rr′∈T.因?yàn)镠(E)?T,所以H(R)?T,即對(duì)于任意r∈H(R),有G(xr,z)=G(x,rz).
引理3.3映射g滿足對(duì)于任意t∈H(A2I),x,y,z,w∈H(A),有
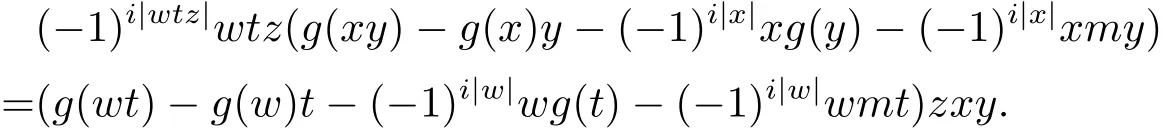
證設(shè) u ∈ H(I),x,y,z,w,w′,w′′∈ H(A),則 uzx,w′′uz,w′w′′u ∈ H(I)? H(R). 由引理3.2,有

設(shè)t=w′w′′u,顯然t∈H(A2I).因此對(duì)于任意x,y,z,w∈H(A)有
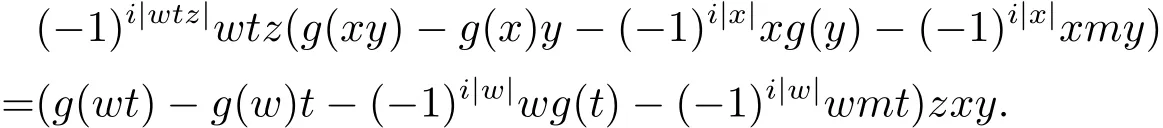
引理3.4設(shè)g是A上滿足(3.1)式的0階線性映射,則(g,m)是A上0階的廣義超導(dǎo)子.
證顯然A2I0.取w∈H(A),t∈H(A2I)滿足wt0.由引理3.3,有
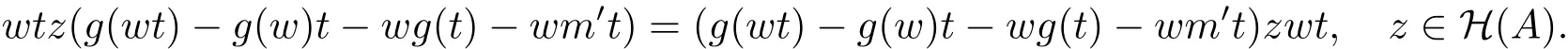
由文獻(xiàn)[11,引理3.2],存在μ∈C0滿足μwt=g(wt)?g(w)t?wg(t)?wm′t.由引理3.3,有
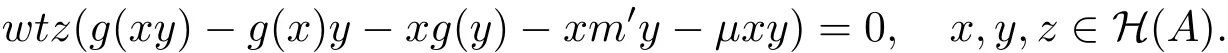
因?yàn)锳是素超代數(shù),所以
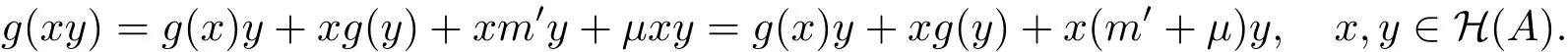
顯然,m′+μ∈A0.令m=m′+μ,則(g,m)是A上0階的廣義超導(dǎo)子.
引理3.5設(shè)g是A上滿足(3.1)式的1階線性映射,則(g,m)是A上1階的廣義超導(dǎo)子.
證取w∈H(A),t∈H(A2I)滿足wt0.
當(dāng)C1=0時(shí),由引理3.3和文獻(xiàn)[11,定理3.5(i)],有

因?yàn)锳是素超代數(shù),所以
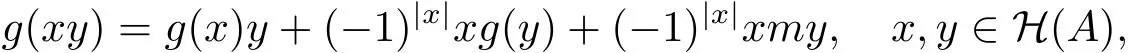
因此(g,m)是A上1階的廣義超導(dǎo)子.
當(dāng)C10時(shí),由引理3.3,對(duì)于任意x,y∈H(A),z0∈A0,有
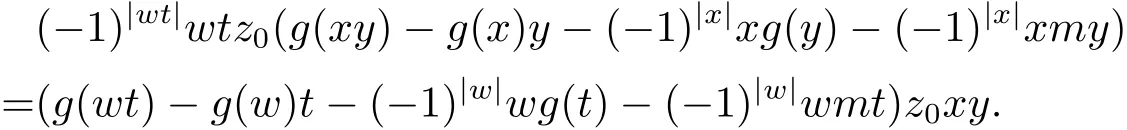
由文獻(xiàn)[11,定理3.5(ii)],對(duì)于任意z1∈A1上式也成立,即
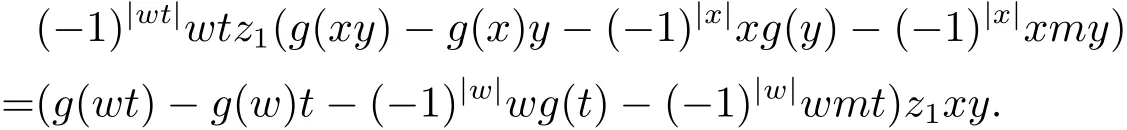
再由引理3.3,對(duì)于任意x,y∈H(A),z1∈A1,有
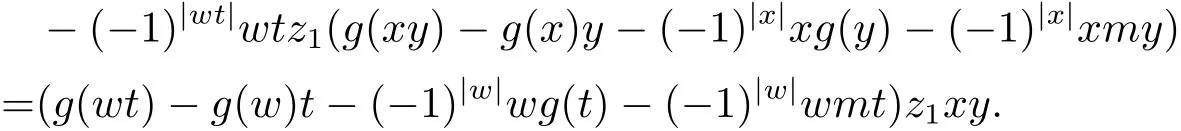
兩式相減有
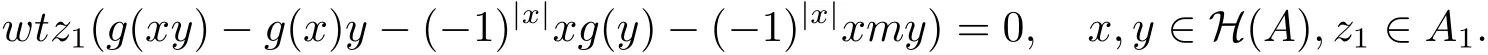
類似地,對(duì)于任意z0∈A0,有
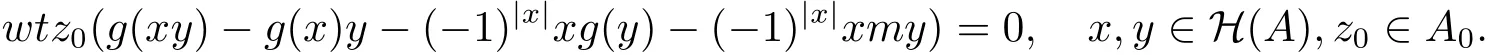
兩式相加有

因?yàn)锳是素超代數(shù),所以g(xy)=g(x)y+(?1)|x|xg(y)+(?1)|x|xmy,x,y∈H(A).因此(g,m)是A上1階的廣義超導(dǎo)子.
參考文獻(xiàn)
[1]Kadison R V.Local derivations[J].J.Alg.,1990,130(2):494–509.
[2]Larson D,Sourour A R.Local derivations and local automorphisms of B(X)[J].Proc.Symp.Pure.Math.,1990,51:187–194.
[3]Bre?ar M,Larson D,Sourour A R.Characterizing homomorphisms,derivations,and multipliers in rings with idempotents[J].Proc.Royal.Soc.Edinburgh,2007,137A:9–21.
[4]Fo?ner A,Fo?ner M.On superderivations and local superderivations[J].Taiwanese J.Math.,2007,11(5):1383–1395.
[5]Bre?ar M.On the distance of the composition of two derivations to the generalized derivations[J].Glasg.Math.J.,1991,33:89–93.
[6]Wang Y.Local generalized derivations in prime rings with idempotents[J].Alg.Coll.,2010,17(2):295–300.
[7]趙延霞,王麗.可換環(huán)上上三角矩陣?yán)畲鷶?shù)的局部自同構(gòu)和局部導(dǎo)子[J].數(shù)學(xué)雜志,2015,35(5):1042–1052.
[8]Nakajima A.On categorical properties of generalized derivations[J].Sci.Math.,1999,2(3):345–352.
[9]Fo?ner A.Local generalized(α,β)-derivations[J].Sci.World J.,2014,2014:1–5.
[10]Yuan H,Wang Y.The product of generalized superderivations on a prime superalgebra[J].Hacet.J.Math.Stat.,2014,43(6):1009–1015.
[11]Fo?ner M.On the extended centroid of prime associative superalgebras with applications to superderivations[J].Comm.Alg.,2004,32(2):689–705.

