DISTRIBUTIVE LATTICES WITH A HOMOMORPHIC OPERATION
LUO Cong-wen,WANG Gao-xia
(College of Science,China Three Gorges University,Yichang 443002,China)
1 Introduction
An algebra L is said to be subdirectly irreducible(s.i)if it has a smallest non-trivial congruence;i.e.,a congruence α,such that θ ≥ α for all θ ∈ ConL with θω.A particularly important case of a subdirectly irreducible algebra is a simple algebra,namely,one for which the lattice of congruence is the two-element chain{ω,ι}.Associated with the notion of a subdirectly irreducible algebra is that of a finitely subdirectly irreducible(f.s.i)algebra,this being de fined as an algebra in which the intersection of two non-trivial principal congruences is non-trivial.Clearly,every s.i.algebra is f.s.i.algebra and f.s.i.semilattices,distributive lattices and Boolean algebras are s.i.Many algebras arising in logic have(distributive)lattice reducts and share the same property;for example,De Morgan algebras[1],the Post algebras of order n,the n-valued Lukasiewicz algebras[2]and demi-p-lattices[3].In this paper,we consider the class of bounded distributive lattices endowed with an unary operation,which is an endomorphism f with f(0)=0,f(1)=1(the class will be denoted by eD),characterise finitely subdirectly irreducible algebras and the subdirectly irreducible algebras in eD.
2 Preminaries
Let(L,f)∈ eD and let f0=id and de fine fnrecursively by fn(x)=f(fn?1(x))for n≥1,then for p,q∈N with p>q≥0,we de fine the subclass ep,qD of eD by adjoining the equation fp=fq.It follows that the smallest nontrivial subclass ep,qD is the class e1,0D,which is determined by the equation f=id.We de fine e2,0D to be the class of symmetric extended distributive lattices,see[4].
A congruence on L is an equivalence relation that has the substitution property for both the lattice operations and for the unary operation f.It follows that every congruence is in particular a lattice congruence and it is essential to distinguish these two types.In order to do so,we shall use the subscript ‘lat’to denote a lattice congruence.
Lemma 2.1(see[5])Let(L,f)∈eD.If a,b∈L with a≤b in L,then
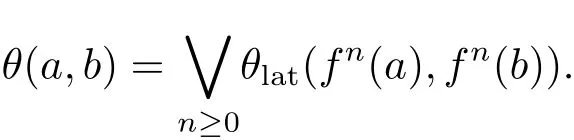
Corollary 2.1Let(L,f)∈e2,0D.Then
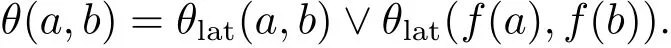
For an algebra(L;f)∈ eD,consider now,for every n ∈ N,the relation Φnon L de fined by
It is clear that Φnis a congruence on L.Moveover,the subset fn(L)={fn(x)|x ∈ L}is a subalgebra of L.
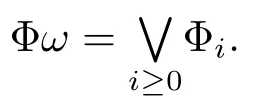
For every non-trivial algebra(L;f)∈eD,it is clear that we have
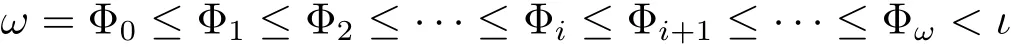
and with ≤ meaning“is a subalgebra of”,
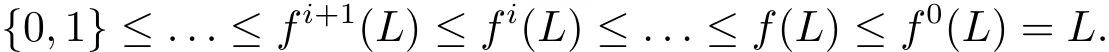
It is readily seen that[x]Φi→ fi(x)describes an algebra isomorphism in eD.We shall denote by writing
The following result is therefore clear.
Lemma 2.2If(L;f)∈ep,qD,then,for n≤q,
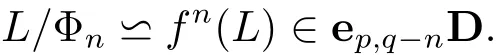
The following two lemmas are an extension to eD-algebras of Blyth for Ockham algebras[6].
Lemma 2.3If(L;f)∈ep,qD,then
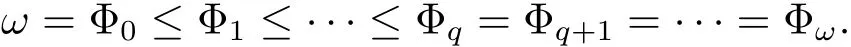
Moreover,if(L;f)belongs to the subclass ep,qD,then each of the above is equivalent to(L;f)∈ ep?q,0D.
Lemma 2.4If(L;f)∈ep,qD,a,b∈L are such that a?b and f(a)=f(b)then θ(a,b)is an atom of ConL.
3 Subdirectly Irreducible Algebras
Given an algebra(L;f)∈eD,consider now for each i≥1 the subset
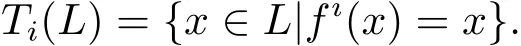
In particular,T1(L)is the set of fixed points of f.Of course,T1(L)is never empty,for it clearly contains 0 and 1.It is readily seen that every subset Tn(L)is a subalgebra of L;in fact Tn(L)is the largest en,0D-subalgebra of L.
Consider now the subset
T(L)={x∈L|there exists a positive integer mxsuch that fmx(x)=x}.
Given x,y∈T(L),let m=lcm{mx,my}.Then,m being positive integer,we have
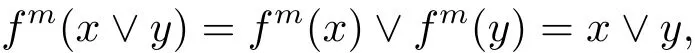
and similarly fm(x∧y)=x∧y.Since x∈T(L)clearly implies f(x)∈T(L),it follows that T(L)is also a subalgebra of L.
Theorem 3.1Let(L;f)∈eD be finitely subdirectly irreducible.Then T1(L)={0,1}.
ProofSuppose that T1(L)contains at least three elements.Then it contains a 3-element chain 0 < a < 1.Then,by Lemma 2.1,we have θ(0,a)= θlat(0,a)and θ(a,1)=θlat(a,1),whence we have the contradiction θ(0,a)∧ θ(a,1)= ω.
Consider now the particular case where L is a finitely subdirectly irreducible symmetry extended distributive lattice.
Lemma 3.1Let L∈e2,0D.Then for x∈L{0,1},either x||f(x),or x=f(x).
Corollary 3.1Let L∈e2,0D be finitely subdirectly irreducible and|L|≥2.Then for x∈L{0,1},x||f(x).
ProofIf x∈L{0,1},then xf(x)according to Theorem 3.1 and so x||f(x)by Lemma 3.1.
Theorem 3.2In the class e2,0D of symmetric extended distributive lattices there are only two( finitely)subdirectly irreducible algebras,each of which is simple,namely,the algebras.
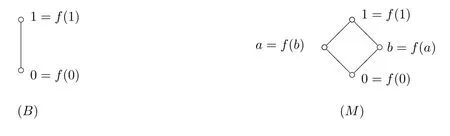
ProofIf|L|=2,then L={0,1}.If|L|=3,let L={0,a,1},then a{0,1}.We have a||f(a)according to Corollary 3.1 and so|L|3,which is absurd.If|L|=4,let L={0,a,b,1},then a,b{0,1}and a||f(a),b||f(b).Thus f(a)=b,f(b)=a.Thus L is M in the above figures.If|L|≥5,then L has 5 distinct points 0,a,b,c,1.If a∧b0,then f(a∧b)0 and a∧b∧f(a∧b)=0,(a∧b)∨f(a∧b)=1 by Theorem 3.1.Since a∧f(a)=0 and b∧f(b)=0,(a∧b)∧f(a∨b)=0 and(a∧b)∨f(a∨b)=1,f(a∨b)=f(a∧b)and so f(a)=f(b),a=b,a contradiction.Thus a∧b=0 and so a∧(f(a)∨b)=0,a∨(f(a)∨b)=1 and therefore
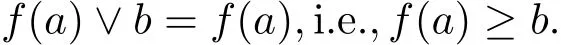
Likely,b∧(f(b)∨a)=0,b∨(f(b)∨a)=1 and therefore f(b)∨a=f(b)and so f(b)≥a and also b≥f(a).Hence we have f(a)=b and so a∨b=1.Also,a∧c=0,a∨c=1.By distributive b=c,a contradiction.
Thus if L is a finitely subdirectly irreducible symmetry extended distributive lattice,then L is only of the two kinds in the above figures.
It is readily seen that for these we have ConB=ConM?2.So these algebras are indeed subdirectly irreducible;in fact,they are simple.
Theorem 3.3If L∈eD is such that T1(L)={0,1}and if a,b∈T(L)are such that a < b then θ(a,b)= ι.
ProofFor every x∈T(L),let mxbe the least positive integer such that fmx(x)=x.Consider the elements
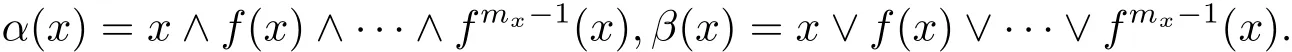
Observe that f(α(x))= α(x)and f(β(x))= β(x),so α(x),β(x)∈ T1(L)={0,1}.Now,let a,b∈T(L)be such that a<b.Consider the sublattice A that is generated by
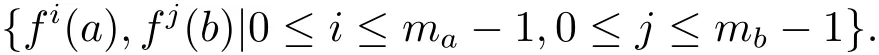
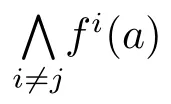
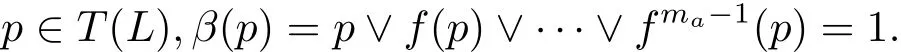
Consequently,A is boolean.
Let c be an atom of A with c/≤ a and c≤ b.Then(0,c)=(a∧c,b∧c)∈ θ(a,b).It follows that(0,f(c))∈ θ(a,b)and so(0,β(c))∈ θ(a,b),i.e.,(0,1)∈ θ(a,b)and therefore θ(a,b)= ι.
Theorem 3.4For an algebra L∈eD the following are equivalent:
(1)T1(L)={0,1};
(2)the subalgebra T(L)is simple;
(3)all symmetric extended distributive sublattices of L are simple.
Proof(1)?(2)If(1)holds,then by Theorem 3.3 every non-trivial principal congruence on T(L)coincides with ι.Since every congruence is the supremum of the principal congruences that it contains,it follows that T(L)is simple.
(2)?(3)T2(L)is the largest symmetric extended distributive sublattice of L.
(3)?(1)If(3)holds,then T2(L)is simple.But T2(L)is a symmetric extended distributive lattice and by Theorem 3.2 there are only two non-isomorphic simple symmetric extended distributive lattices,in each of which T1(T2(L))={0,1}.Since T2(L)and L have the same fixed points,(1)follows.
Theorem 3.5If L ∈ eD is finitely subdirectly irreducible,then every Φ1-class in L contains at most two elements.
ProofSuppose that a Φ1-class contains at least three elements.Then it contains a 3-element chain x < y < z with f(x)=f(y)=f(z).Then,by Lemma 2.1,we have θ(x,y)=θlat(x,y)and θ(y,z)= θlat(y,z),whence we have the contradiction θ(x,y)∧ θ(y,z)= ω.
Theorem 3.6If L∈ep,qD then the following statements are equivalent:
(1)L is finitely subdirectly irreducible;
(2)L is subdirectly irreducible.
Proof(1)? (2)Since L ∈ep,qD,for every x∈ L,we have fp(x)=fq(x).If Φ1= ω,then f is injective and x=fp?q(x),whence x ∈ T(L).Thus L=T(L)and it follows by Theorem 3.1 and Theorem 3.4 that L is simple,hence subdirectly irreducible.
On the other hand,if Φ1ω,then by Theorem 3.5 there is a two-element Φ1-class{a,b},and by Lemma 2.4, θ(a,b)is an atom in the interval[ω,Φ1]of ConL.If now α ∈ConL with αω then,since α is the supremum of the non-trivial principal congruences which it contains and since ConL satis fies the in finite distributive law β∧∨γi= ∨(β ∧γi),it follows by the hypothesis that L is finitely subdirectly irreducible that θ(a,b)∧ α = θ(a,b)and hence θ(a,b) ≤ α.Thus θ(a,b)is the smallest non-trivial congruence on L,so L is subdirectly irreducible.
(2)?(1)This is clear.
The following theorem is an extension to eD-algebras of Blyth for Ockham algebras,see[6].
Theorem 3.7L∈ep,qD is subdirectly irreducible if and only if Con L reduces to the finite chain
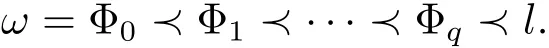
References
[1]Balbes R,Dwinger Ph.Distributive lattices[M].Columbia:Univ.Missouri Press,1974.
[2]Beazer R.Finitely subdirectly irreducible algebras with pseudocomplementation[J].Algebra Universalis,1981,12:376–386.
[3]Gramaglia H,Vaggione D J.(Finitely)subdirectly irreducibles and Birkhoff-like sheaf representation for certain varieties of lattice ordered structures[J].Algebra Universalis,1997,38(1):56–91.
[4]Luo C W,Guo L.On idempotent extended distributive lattices whose congruences are permutable[J].J.Math.,2015,35(2):407–411.
[5]Fang J.Distributive Lattices with unary operations[M].Beijing:Science Press,2011.
[6]Blyth T S,Varlet J C.Ockham Algebras[M].Oxford:Oxford University Press,1994.
[7]Berman J.Distributive Lattices with an additional unary operation[J].Aequationes Math.,1977,16:165–171.
[8]Blyth T S,Jie F.Extended Ockham Algebras[J].Commun.Algebra,2000,28(3):1271–1284.

