COMMUTATORS GENERATED BY LUSIN-AREA INTEGRAL AND LOCAL CAMPANATO FUNCTIONS ON GENERALIZED LOCAL MORREY SPACES
MO Hui-xia,MA Rui-qing,WANG Xiao-juan
(School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China)
1 Introduction
Suppose that Sn?1is the unit sphere in Rn(n ≥ 2)equipped with the normalized Lebesgue measure dσ.Let ? ∈ Ls(Sn?1)(1<s≤∞)be homogeneous of degree zero and satisfy the cancellation condition

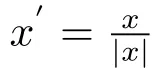
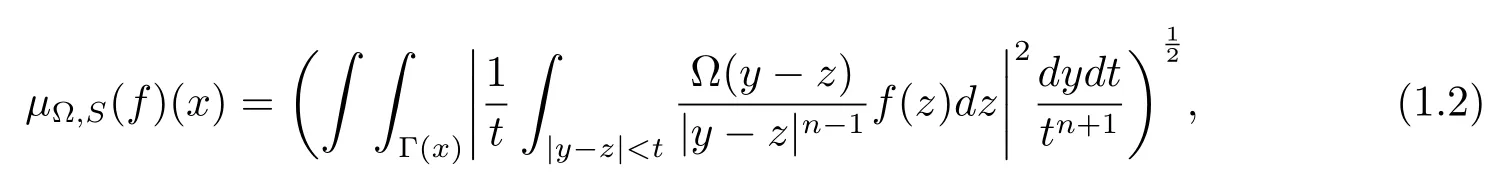
where
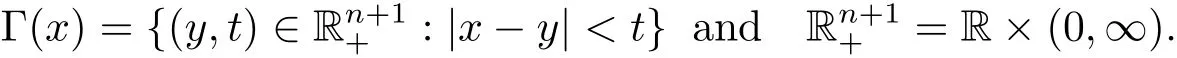
Moreover,letwhere bi∈ Lloc(Rn)for 1 ≤ i≤ m.Then the multilinear commutator generated byand μ?,Scan be de fined as follows:
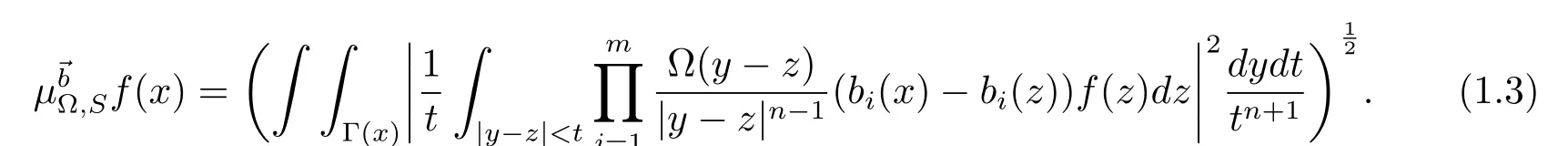
It is well known that the Lusin-area integral plays an important role in harmonic analysis and PDE(for example,see[1–8]).Therefore,it is a very interesting problem to discuss the boundedness of the Lusin-area integral.In[2],Ding,Fan and Pan studied the weighted Lpboundedness of the area integralμ?,S.In[3],the authors investigated the boundeness ofμ?,Son the weighted Morrey spaces.The commutators generated by μ?,Sattracted much attention too.In[5]and[6],the authors discussed the weighted Lpboundedness and endpoint estimates for the higher order commutators generated by μ?,Sand BMO function,respectively.In[8],the authors showed that the commutator generated by μ?,Sand V MO is a compact operator in the Morrey space.
Moreover,the classical Morrey space Mp,λwere first introduced by Morrey in[9]to study the local behavior of solutions to second order elliptic partial differential equations.And,in[10],the authors introduced the local generalized Morrey spaceand they also studied the boundedness of the homogeneous singular integrals with rough kernel on these spaces.
Motivated by the works of[2,3,5,8,10,13],we are going to consider the boundedness ofμ?,Son the local generalized Morrey spaceas well as the boundedness of the commutators generated by μ?,Sand local Campanato functions.
2 Some De finitions and Lemmas
De finition 2.1[10]Let ?(x,r)be a positive measurable function on Rn× (0,∞)and 1≤p≤∞.For any fixed x0∈Rn,a function fis said to belong to the local Morrey space,if
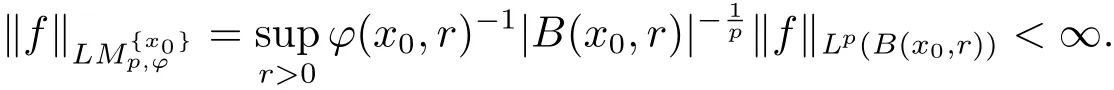
And we denote
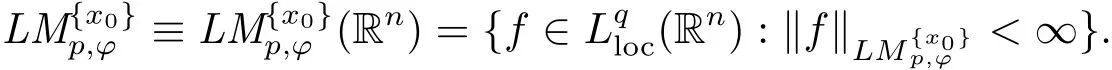
According to this de finition,we recover the local Morrey spaceunder the choice
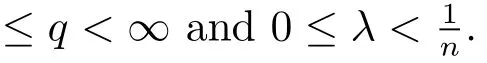
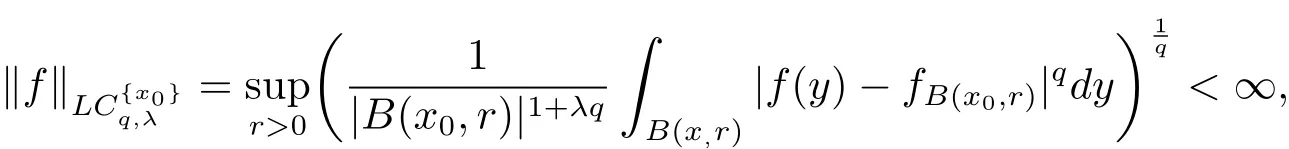
where
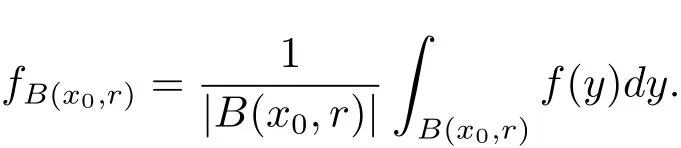
De fine

Remark 2.1[10]Note that,the central BMO spaceandMoreover,imagining that the behavior ofmay be quite different from that of BMO(Rn),since there is no analogy of the John-Nirenberg inequality of BMO for the space
Lemma 2.1[10]Let 1then
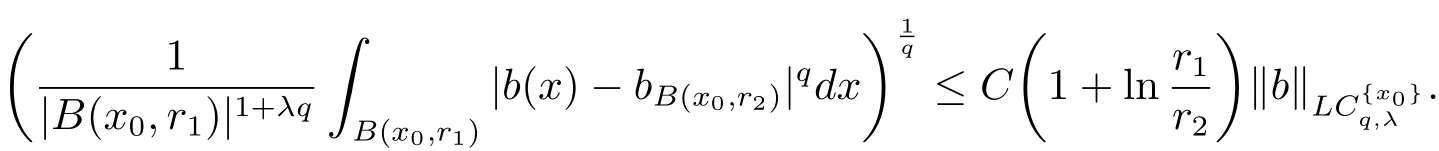
And from this inequality,we have

In this section,we are going to use the following statement on the boundedness of the weighted Hardy operator

where w is a fixed function non-negative and measurable on(0,∞).
Lemma 2.2[11,12]Let v1,v2and w be positive almost everywhere and measurable functions on(0,∞).The inequality
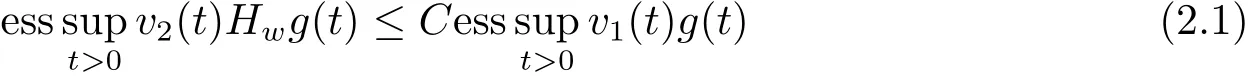
holds for some C>0 and all non-negative and non-decreasing g on(0,∞)if and only if

Moreover,ifis the minimum value of C in(2.1),then=B.
Lemma 2.3[2]Suppose that 1< q,s≤ ∞ and ? ∈ Ls(Sn?1)satisfying(1.1).If q,s and weighted function w satisfy one of the following conditions
(i)max{s′,2}= η < q < ∞,and w ∈ Aq/η;
(ii)2 < q < s,and w1?(q/2)′∈ Aq′/s′;
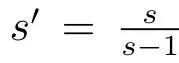
Remark 2.2From Lemma 2.3,it’s obvious that when ? ∈ Ls(Sn?1)(1 < s ≤ ∞)satis fies condition(1.1),the operatorμ?,Sis bounded on Lq(Rn)space for 2≤ q< ∞.
3 Lusin-Area Integral on Generalized Local Morrey Spaces
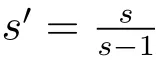
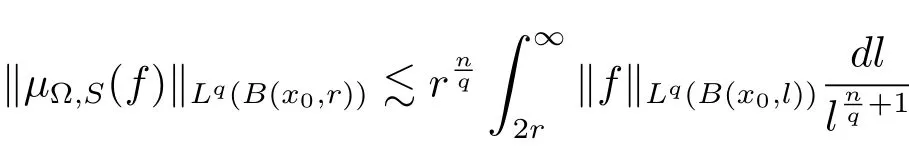
holds for any ball B(x0,r).
ProofLet B=B(x0,r).We write f=f1+f2,where f1=fχ2Band f2=fχ(2B)c.Thus we have
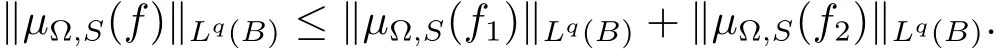
Since μ?,Sis bounded on Lq(Rn)space(see Lemma 2.3),then it follows that
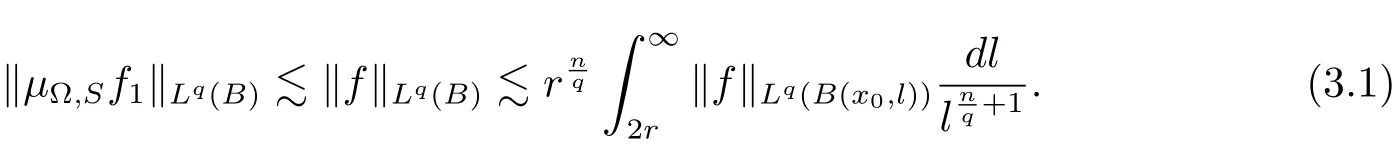
Our attention will be focused now on
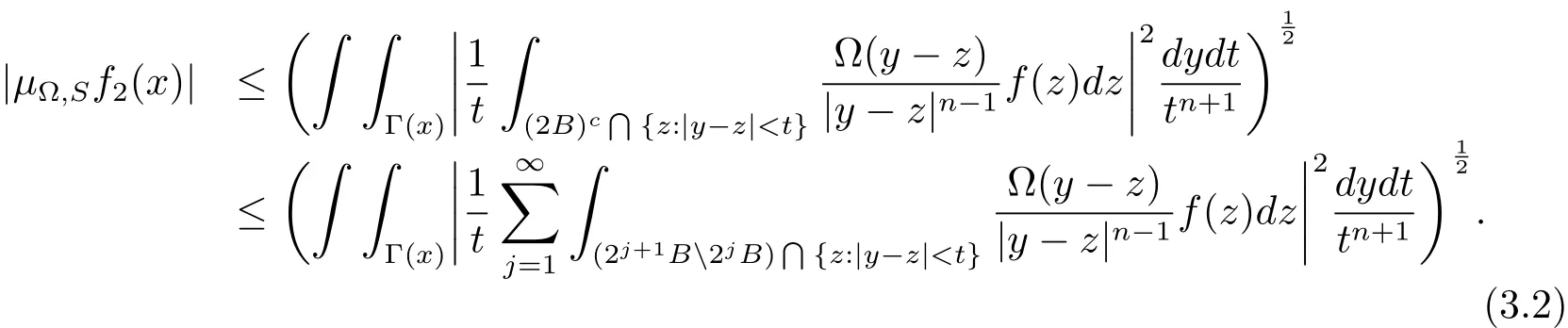
Without loss of generality,we can assume that for any x∈B,(y,t)∈Γ(x)and z∈2j+1B2jB,we haveThus there existssuch that
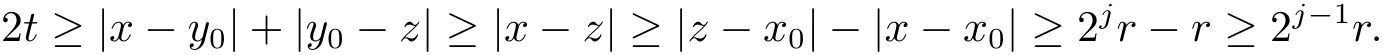
Hence
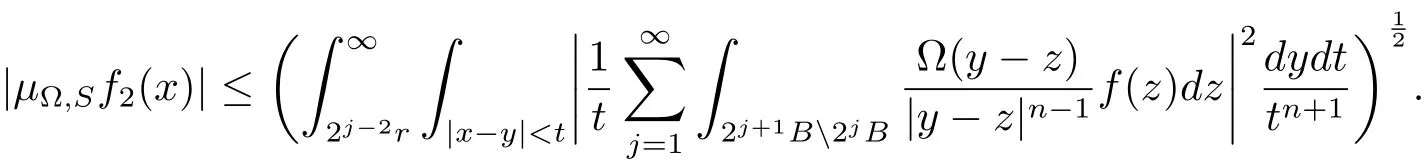
When ? ∈ L∞(Sn?1),it follows from the Hlder’s inequality that
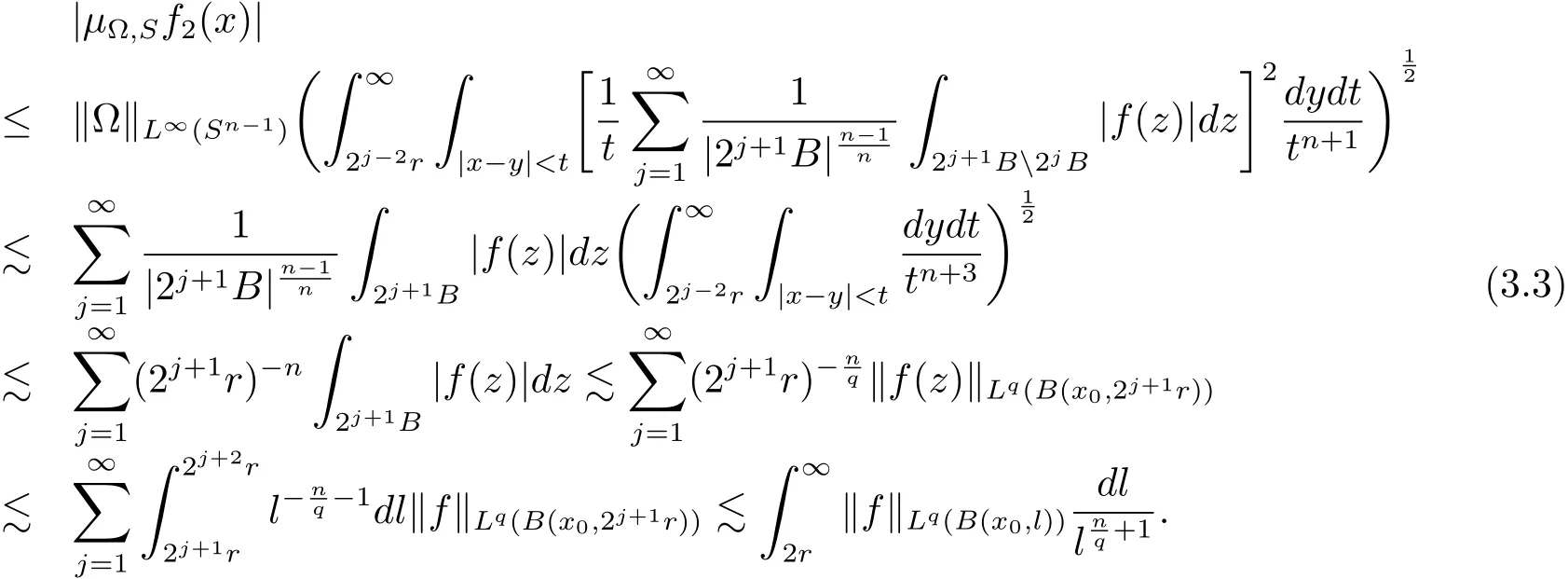
When ? ∈ Ls(Sn?1),1 < s < ∞,it is obvious that
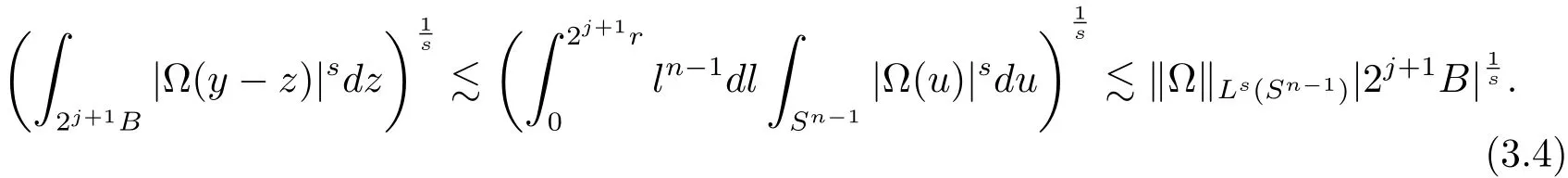
Thus from H?lder’s inequality and(3.4),we have
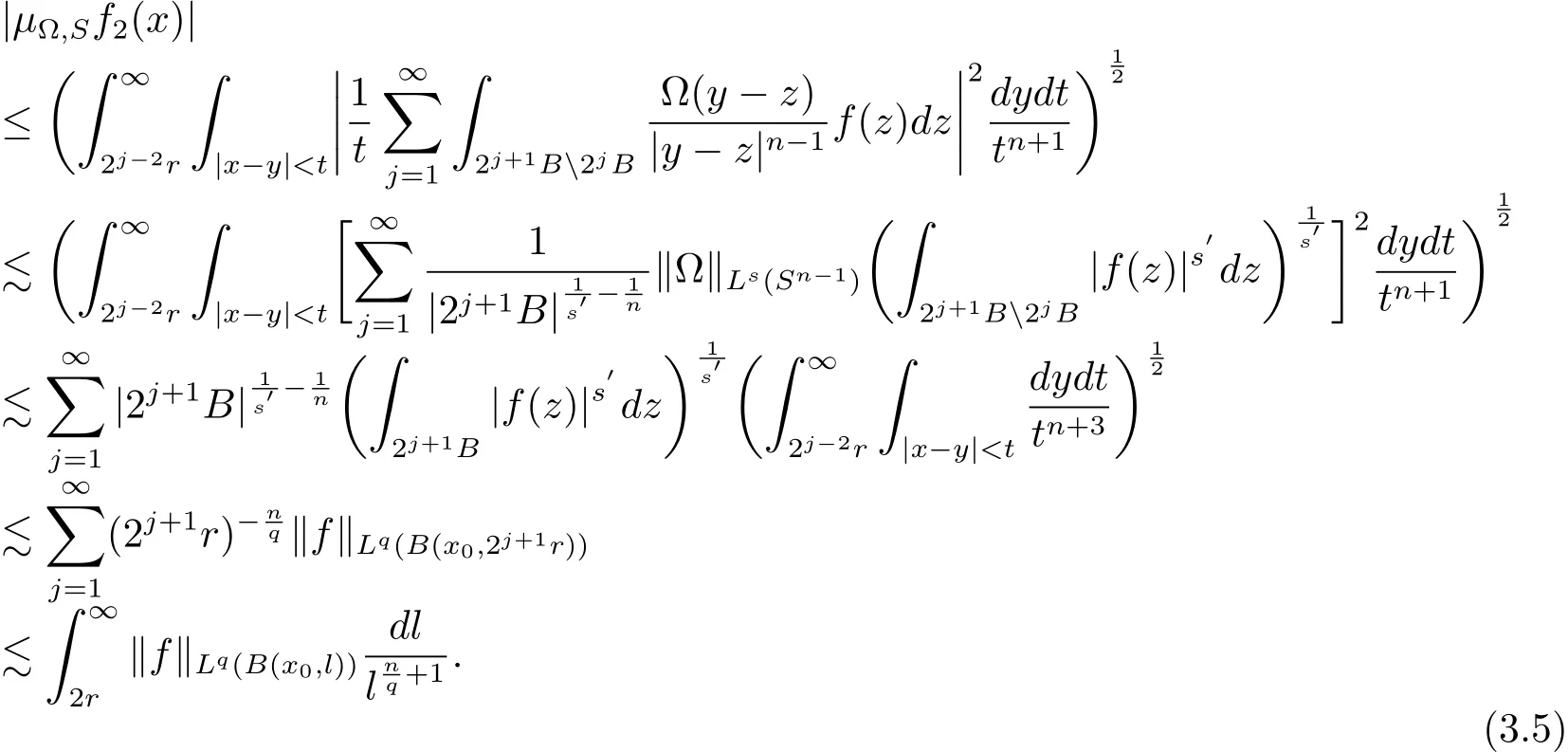
So
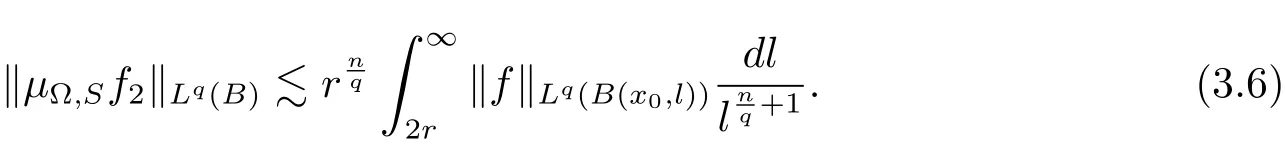
Therefore combining(3.1)and(3.6),we have
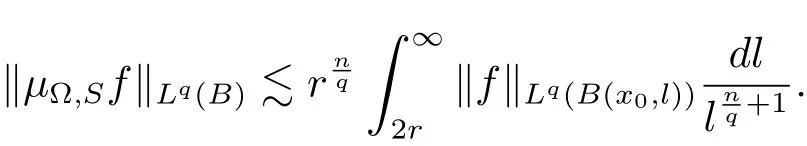
Thus we complete the proof of Theorem 3.1.
Theorem 3.2Let ? ∈ Ls(Sn?1)(1 < s ≤ ∞)satisfy condition(1.1)and max{2,s′} <q< ∞.Then,if functions ?,ψ :Rn×(0,∞)→ (0,+∞)satisfy the inequality
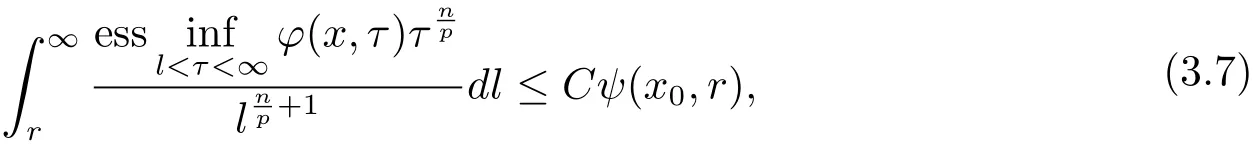
where C does not depend on x and r,the operatorμ?,Sis bounded from
ProofTakingandthen from Theorem 3.1,we have
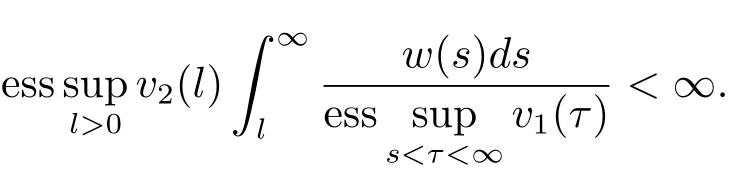
Thus from Lemma 2.2,it follows that

Therefore
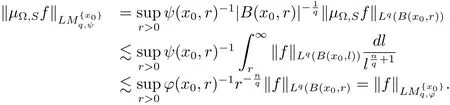
Thus we complete the proof of Theorem 3.2.
4 Commutators Generated by Lusin-Area Integral on Generalized Local Morrey Spaces
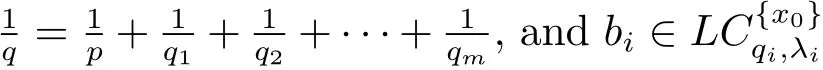
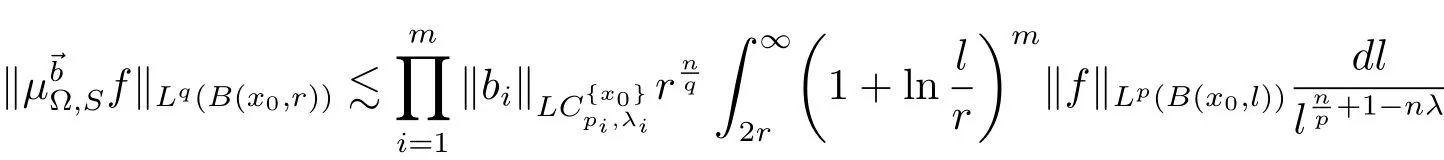
holds for any ball B(x0,r),where λ = λ1+ λ2+ ···+ λm.
ProofWithout loss of generality,it is sufficient for us to show that the conclusion holds for m=2.
Let B=B(x0,r).And we write f=f1+f2,whereThus we have
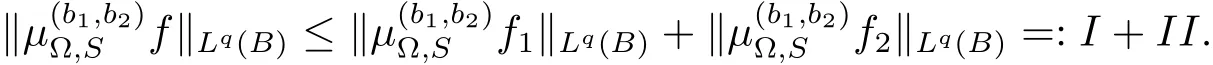
Let us estimate I and II,respectively.It is obvious that
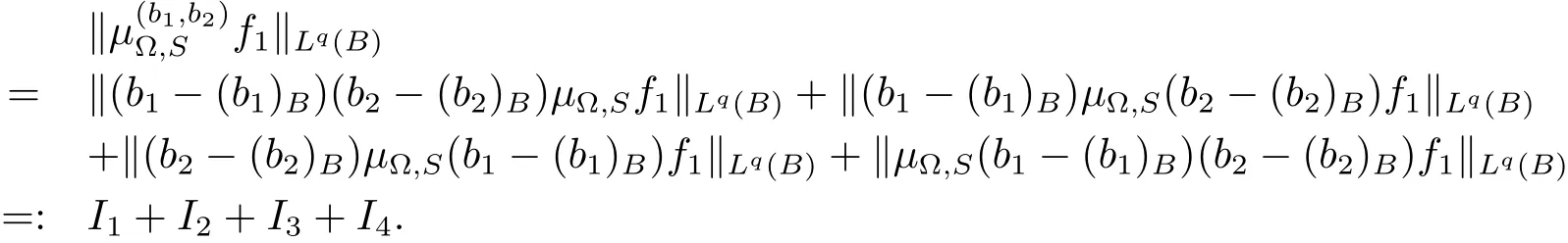
From Lemma 2.1,it is easy to see that
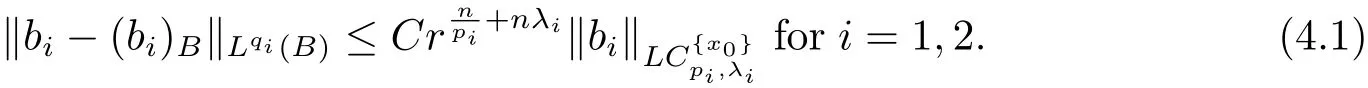
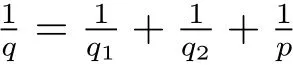
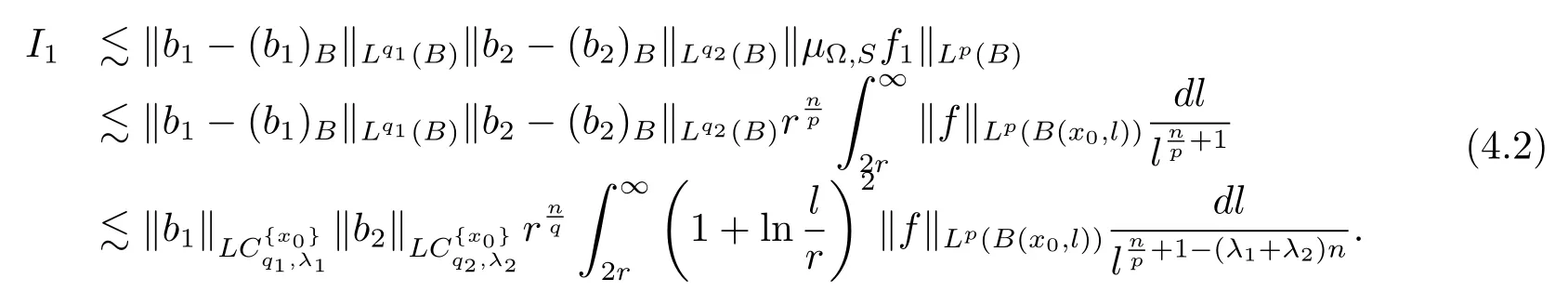
Moreover,from Lemma 2.1,it is easy to see that
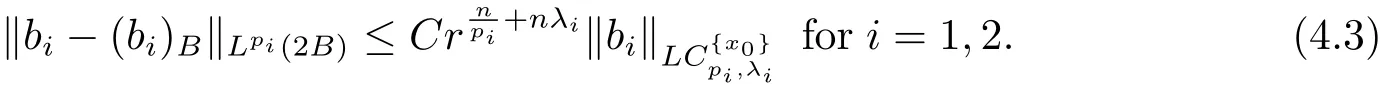
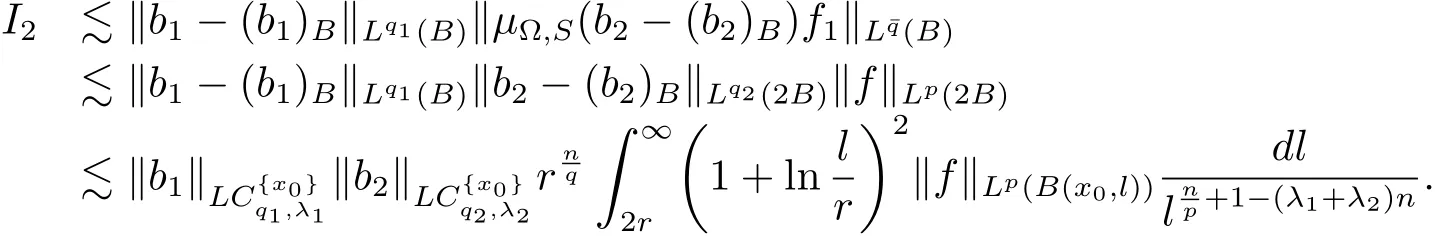
Similarly,
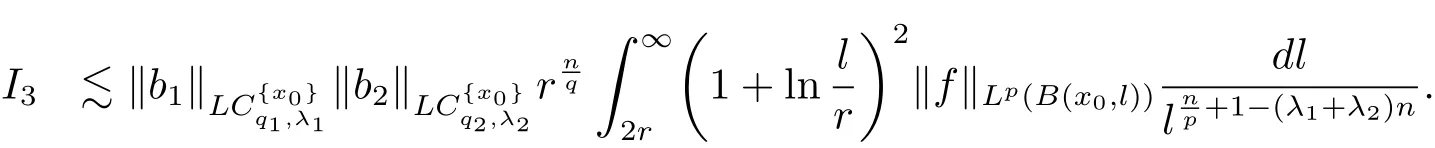
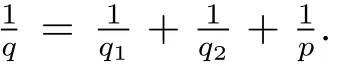
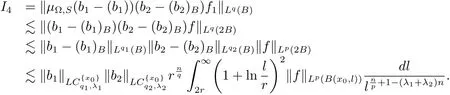
Therefore combining the estimates of I1,I2,I3and I4,we have
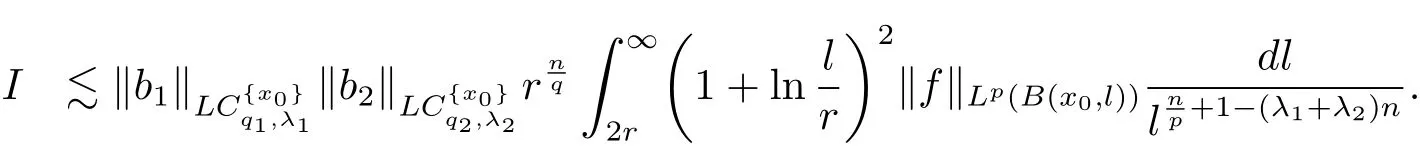
Let us estimate II.
SinceThen using H?lder’s inequality and(3.6),we have
In the following,let us estimate II2.For x ∈ B,when ? ∈ L∞(Sn?1),from Lemma 2.1 and estimate of(3.3),we have

For x∈B,when ? ∈ Ls(Sn?1),1< s< ∞,from Lemma 2.1 and the estimate of(3.5),it follows that
Let 1<<∞such thatthenand max{2,s′}<< ∞.Thus,from H?lder’s inequality,(4.4)and(4.5),we obtain
Similarly,
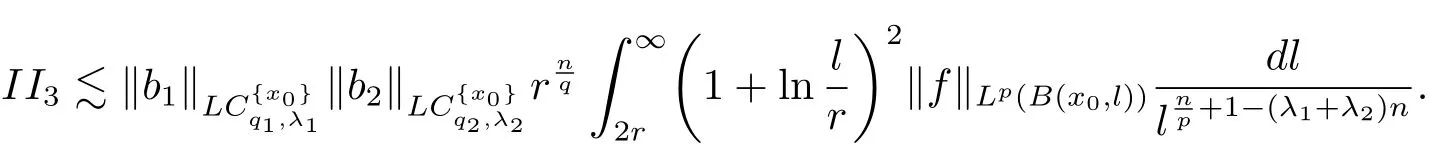
Let us estimate II4.It is analogue to the estimates of(4.4),(4.5)and(4.6),we have the following estimates.
When x∈ B,? ∈ L∞(Sn?1),we have
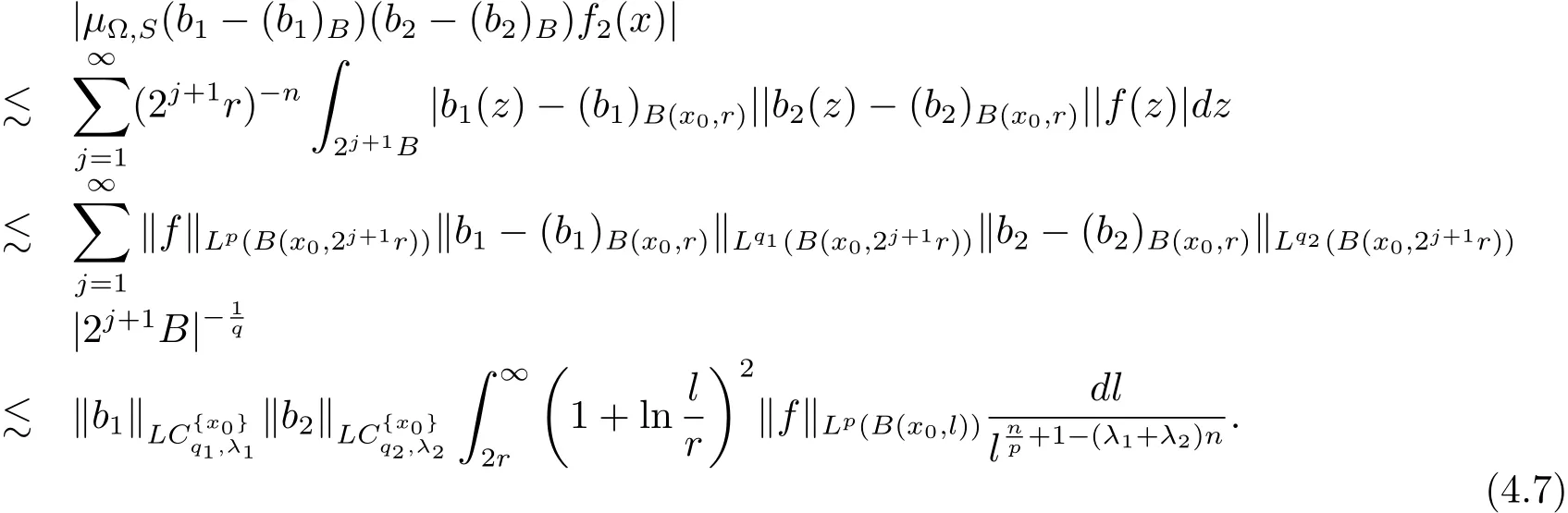
When x∈B,?∈Ls(Sn?1),1<s<∞,we have
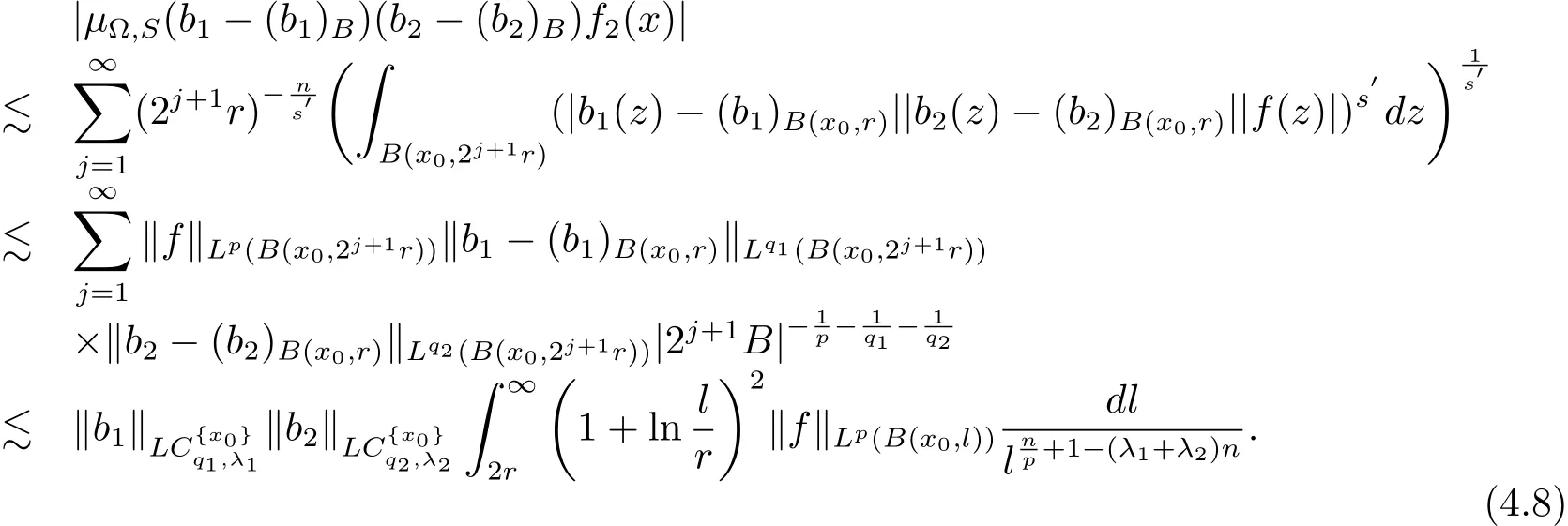
Therefore from(4.7)and(4.8),we have
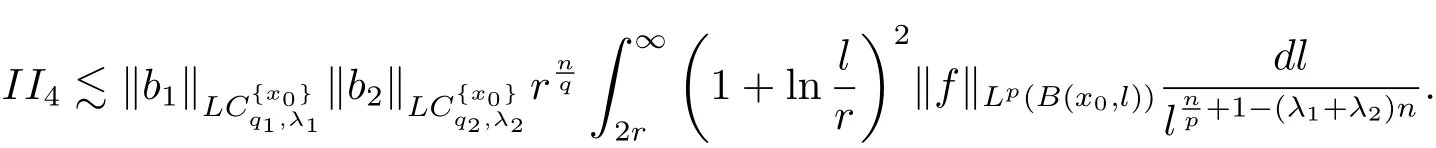
So from the estimates of II1,II2,II3and II4,it follows that
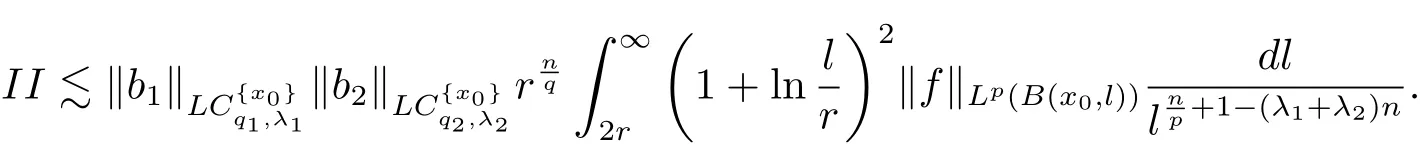
Therefore from the estimates of I and II,we deduced that
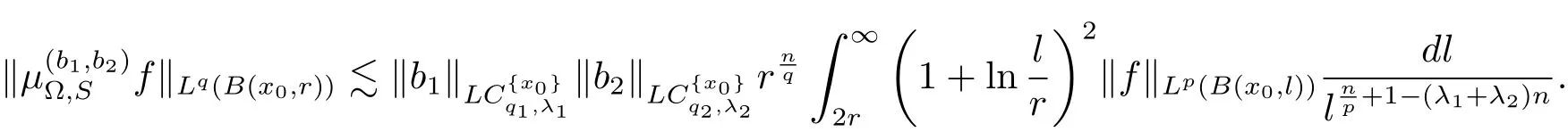
Thus the proof of Theorem 4.1 is completed.
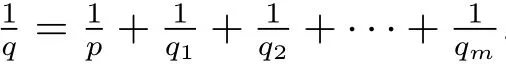
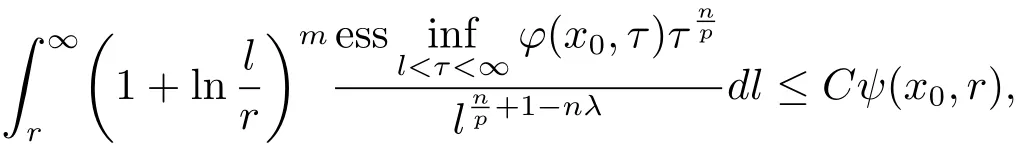
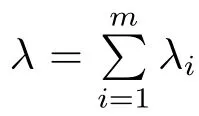
ProofTakingand.It is easy to see that
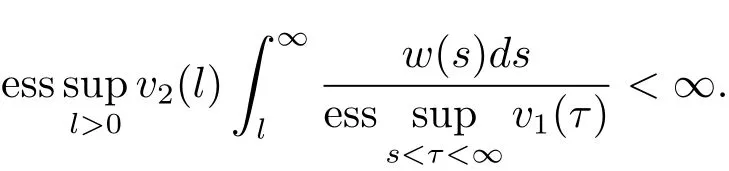
Thus by Lemma 2.2,we have
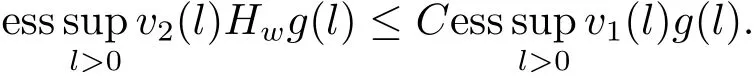
So
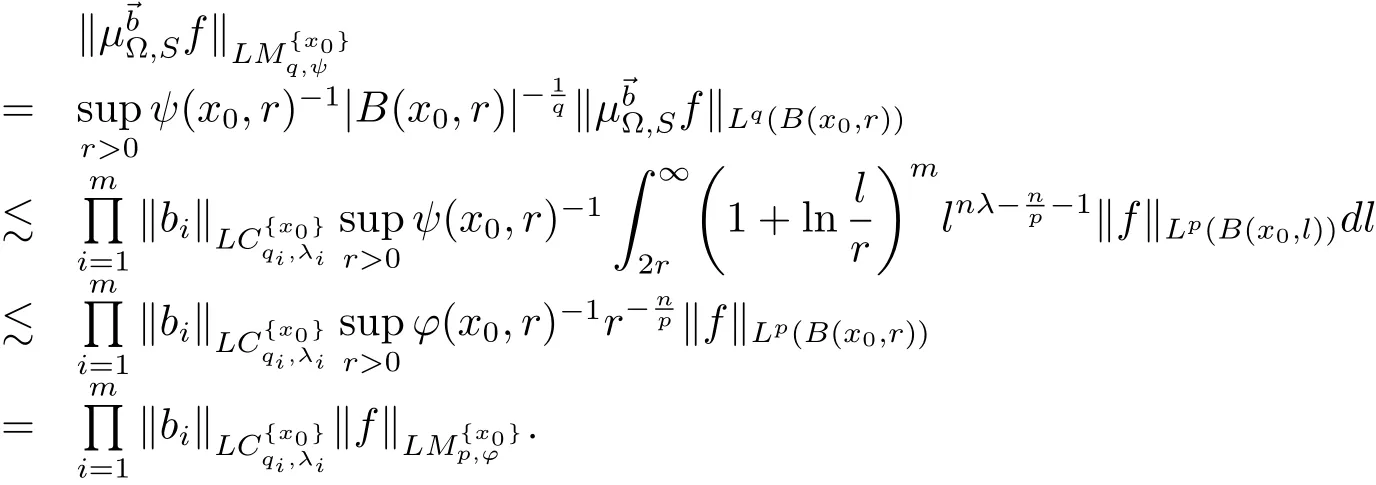
Thus the proof of Theorem 4.2 is finished.
References
[1]Chang S Y A,Wilson J M,Wolff T H.Some weighted norm inequalities concerning the Schr?dinger operators[J].Comment.Math.Helv.,1985,60(1):217–246.
[2]Ding Y,Fan D S,Pan Y B.Weighted boundedness for a class of rough Marcinkiewicz integrals[J].India Univ.Math.J.,1999,48(3):1037–1055.
[3]Tao S P,Wei X M.Boundeness of Littlewood-Paley operators with rough kernels on the weighted Morrey spaces[J].J.Lanzhou Univ.,2013,49(3):400–404.
[4]Lin Y,Liu Z G,Mao D L,Sun Z K.Parameterized Littlewood-Paley operators and area integrals on weak Hardy spaces[J].Acta.Math.Sin.,2013,29(10):1857–1870.
[5]Ding Y,Lu S Z,Yabuta K.On commutators of Marcinkiewicz integrals with rough kernel[J].J.Math.Anal.Appl.,2002,275(1):60–68.
[6]Ding Y,Xue Q Y.Endpoint estimates for commutators of a class of Littlewood-Paley operators[J].Hokkaido.Math.J.,2007,36(2):245–282.
[7]Chen Y P,Ding Y,Wang X X.Commutators of Littlewood-Paley operators on the generalized Morrey space[J].J.Inequal.Appl.,2010(1),Artical ID:961502,20 pages.
[8]Chen Y P,Wang H.Compactness for the commutator of the parameterized area integral in the Morrey space[J].Math.Inequal.Appl.,2015,18(4):1261–1273.
[9]Morrey C B.On the solutions of quasi-linear elliptic partial differential equations[J].Trans.Amer.Math.Soc.,1938,43(1):126–166.
[10]Balakishiyev A S,Guliyev V S,Gurbuz F,Serbetci A.Sublinear operators with rough kernel generated by Calder′on-Zygmund operators and their commutators on generalized local Morrey spaces[J].J.Inequ.Appl.,2015,2015(1):1–18.
[11]Guliyev V S.Local generalized Morrey spaces and singular integrals with rough kernel[J].Azerb.J.Math.,2013,3(2):79–94.
[12]Guliyev V S.Generalized local Morrey spaces and fractional integral operators with rough kernel[J].J.Math.Sci.,2013,193(2):211–227.
[13]Zhang L,Zheng Q.Boundedness of commutators for singular integral operators with oscillating kernels on weighted Morrey spaces[J].J.Math.,2014,34(4):684–690.

