Jiafeng LIAO(廖家鋒)Yang PU(蒲洋)

School of Mathematics and Statistics,Southwest University,Chongqing 400715,China School of Mathematics and Information,China West Normal University,Nanchong 637002,China

E-mail:liaojiafeng@163.com;172431794@qq.com

Chunlei TANG(唐春雷)?

School of Mathematics and Statistics,Southwest University,Chongqing 400715,China

E-mail:tangcl@swu.edu.cn

1 Introduction and Main Result

In this article,we study the following concave-convex elliptic equations involving critical Sobolev exponent

where ??RN(N≥3)is an open bounded domain with smooth boundary,1＜q＜2,λ＞0.is the critical Sobolev exponent for the embedding ofinto Lp(?)for everywhereis a Sobolev space equipped with the normThe coefficient function f ∈ Lr(?)is nonzero and nonnegative,whereAnd g ∈ C(?)is a positive function.

More precisely,we say that a functionis called a weak solution of problem(1.1),if for allthere holds

where u+=max{u,0}.

It is well known that the pioneer work is Brézis and Nirenberg[4],that is,the existence of positive solutions of semilinear elliptic equations involving critical exponent is related to the dimension of space.After that,semilinear elliptic problems with critical exponent were extensively considered(see[1,2,5,7–30,33,35–37,39–42]).Particularly,Ambrosetti,Brézis,and Cerami[2]studied the following problem

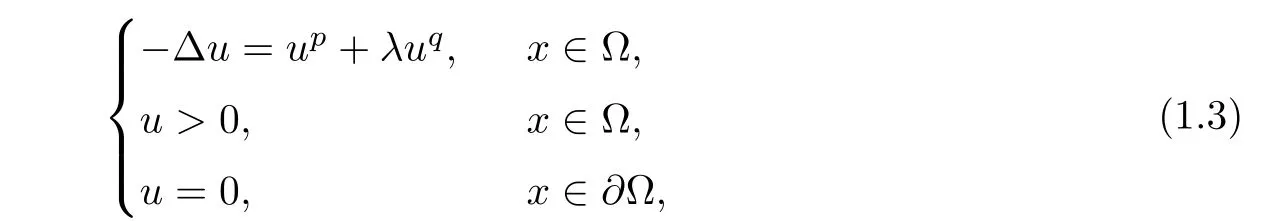
where 0＜q＜1＜ p≤ 2??1.They obtained the classic results by the sub-supersolution method and variational method,that is,there exists λ0＞ 0 such that problem(1.3)has at least two positive solutions for λ ∈ (0,λ0),a positive solution for λ = λ0,and no positive solution for λ ＞ λ0.After that,many authors considered the concave-convex-type elliptic problems(see[1,9,14,20,21,24–28,35,40]).Particularly,Korman in[22]considered the exact number of positive solutions for problem(1.3)in the unit ball B?RN(N≥3).By the bifurcation theory,it is obtained that there exists a critical number＞0 such that problem(1.3)has two positive solutions for λ ∈(0,),exactly one positive solution for λ=,and no positive solution for λ＞.As any positive solution to problem(1.3)in the unit ball B is radial,Tang in[35]proved this result of[22]by an ordinary differential equation method.In[1],Ambrosetti,Azorer,and Peral studied problem(1.3)in RN(N≥3),that is,

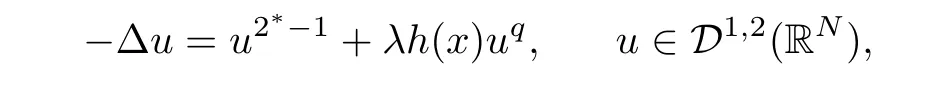
where 0＜ q＜ 1,h ∈ L1(RN)∩L∞(RN).When h ≥ 0,h/≡ 0,and λ ＞ 0 small enough,they obtained two positive solutions.Moreover,[9,14]and[20]considered the multiplicity of positive solutions for concave-convex p-Laplacian problems with critical Sobolev exponent.

Recently,Lin considered problem(1.1)under the following conditions in[28].

(h1)

(h2)There exist k points a1,a2,···,akin ? such that

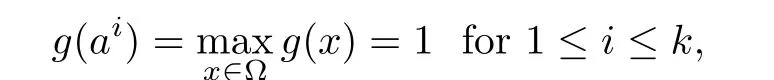
and for some σ ＞ N such that g(x)?g(ai)=O(|x? ai|σ)as x → aiuniformly in i.(h3)Choosing r0＞0 such thatwhereThere exists a positive number d0such that f(x)≥d0＞0 for any

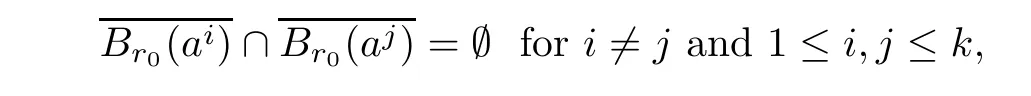
For the convenience of the reader,we repeat the main results of[28]as follows.

Theorem 1.1Assume thatand(h1)–(h3)hold,then problem(1.1)has k+1 positive solutions for λ＞0 small enough.Moreover,one of the solutions is a ground state solution.

Moreover,Cao and Chabrowski in[7]considered problem(1.1)with q=1 and obtained the multiplicity of positive solutions.Very recently,we studied problem(1.1)with 2≤ q＜ 2?and obtained some existence and multiplicity results by the variational method;see[27].

In this article,an interesting question is whether there exist k+1 positive solutions for problem(1.1)without constraining conditions of＜q＜2 and N ＞4.We are interested in the existence of k+1 positive solutions for problem(1.1)with 1＜q＜2 and N≥3.Wefind the reason of restricting＜q＜2 and N ＞4 in[28]is that the author obtained k positive solutions from the prolongation of the origin.Now,we try to get rid of the constraining conditions of＜q＜2 and N＞4 via obtaining k positive solutions from the prolongation of the first solution.In fact,the first solution is a positive ground state solution of problem(1.1).

We denote by|·|pthe usual Lp-norm.Let S be the best Sobolev constant and Λ be a constant,respectively,

As well known,the function

is an extremal function for the minimization problem(1.4),that is,it is a positive solution of the following problem

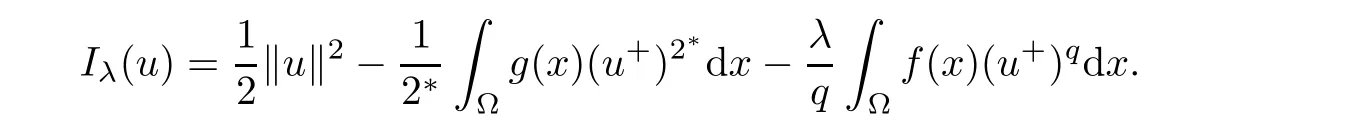
From the result in[31],one knows that the functional Iλis of class C1on(?).As well known that there exists a one to one correspondence between the nonnegative solutions of problem(1.1)and the critical points of Iλon(?).

In this article,assume that the coefficient functions f,g satisfy the following conditions:

(f)f ∈ Lr(?)with f ≥ 0 and f/≡ 0,where

(g)g is continuous on ? and g＞ 0.

(h′2)There exist k points a1,a2,···,akin ? satisfying

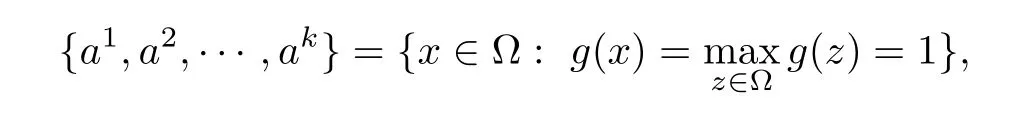
Notice that u is a weak solution of problem(1.1),then u satisfies the following equation

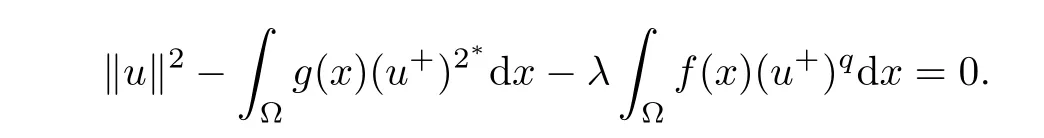
So,if such a solution exists,then it must lie in Nehari manifold N,which is defined by

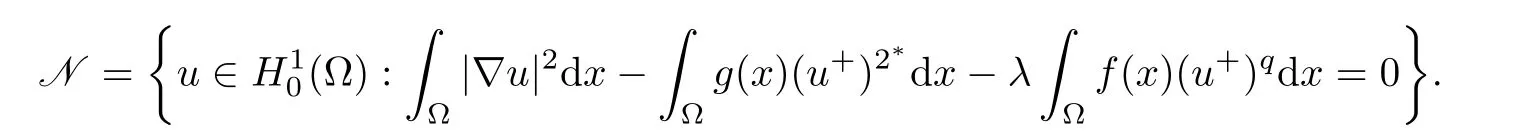
To obtain the multiplicity of positive solutions,we split N=N+∪N0∪N?with N+,N0,N?defined as follows:

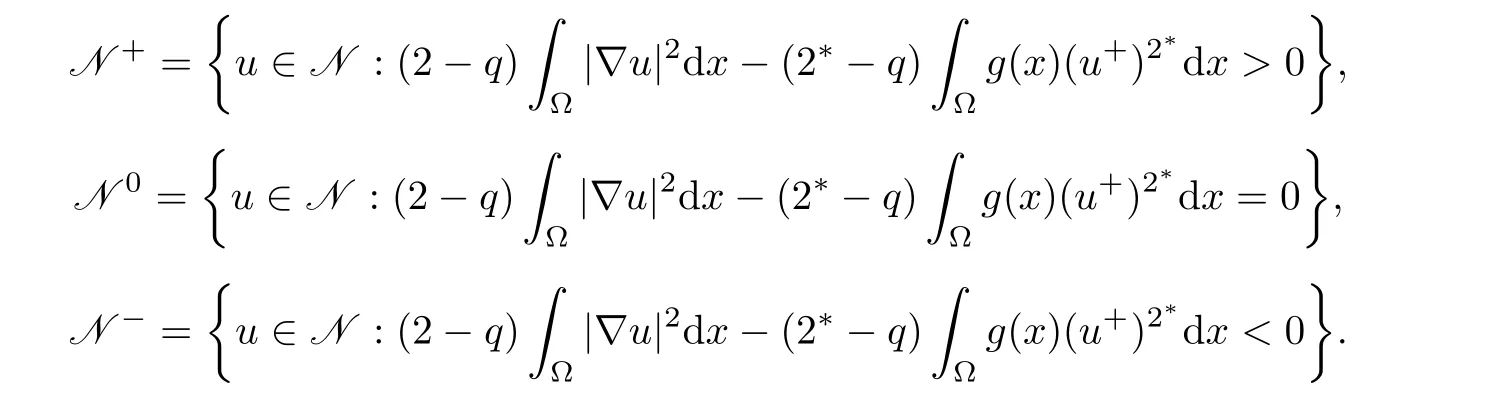
When λ ∈ (0,Λ),we will prove that N±/= ? and N0={0}in Section 2.

Here is our main result.

Theorem 1.2Assume that 1 ＜ q ＜ 2,N ≥ 3,and f,g satisfy(f),(g)andthen there exists Λ?＞ 0 such that for λ ∈ (0,Λ?),problem(1.1)has at least k+1 positive solutions.Moreover,there exists one solution uλwhich is a ground state solution with Iλ(uλ) → 0 and‖uλ‖ → 0 as λ → 0+.

Remark 1.3To our best knowledge,our results are up to date.Our results complement the case of 1＜q≤in[28],and we also obtain the same results but without restricting N ＞4.It is worth noticing that the growth condition inthat is,as x→aiuniformly in i∈N+and 1≤i≤k,which is more general than the corresponding condition of(h2)in[28].Moreover,we get rid of the condition(h3)which is important for estimating the level value of functional Iλin Lemma 4.2 of[28].

This article is organized as follows.In Section 2,we give some preliminaries.We give the proof of existence of a positive ground state solution of problem(1.1)in Section 3.In Section 4,we give the proof of Theorem 1.2.

2 Some Preliminary Results

In this section,we give some lemmas about properties of the functional Iλon N,which are valuable preparation for the proof of our main result.

Lemma 2.1For eachsuch thatwe have the followings:

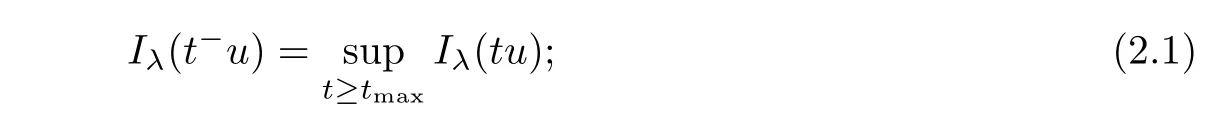
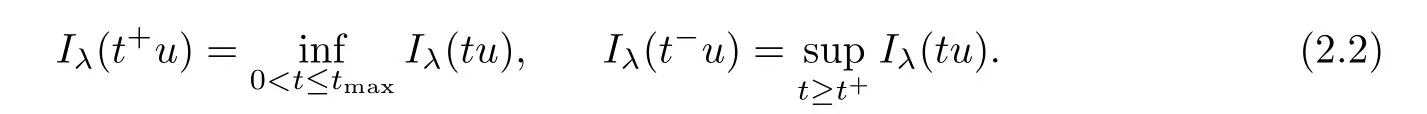
Furthermore,N0={0}and N?is a closed set for all 0＜λ＜Λ.

ProofAccording to(g),there existssuch thatFor eachsuch thatFor all t≥0,we define k:R+→R by

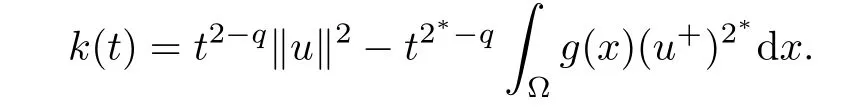
Clearly,we obtain k(0)=0 and k(t)→?∞ as t→∞.Because

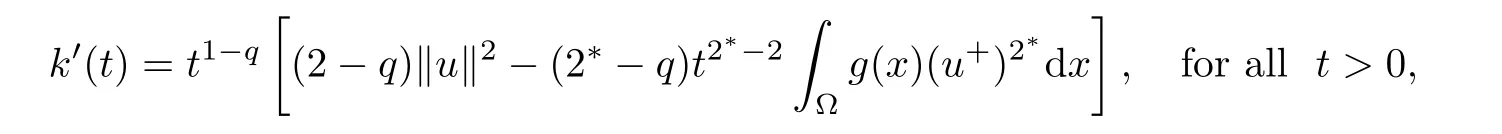
then k′(tmax)=0,k′(t)＞ 0 for 0 ＜ t＜ tmax,and k′(t)＜ 0 for t＞ tmax,where

Thus,k(t)achieves its maximum at tmax.Moreover,by the Sobolev embedding theorem,one has

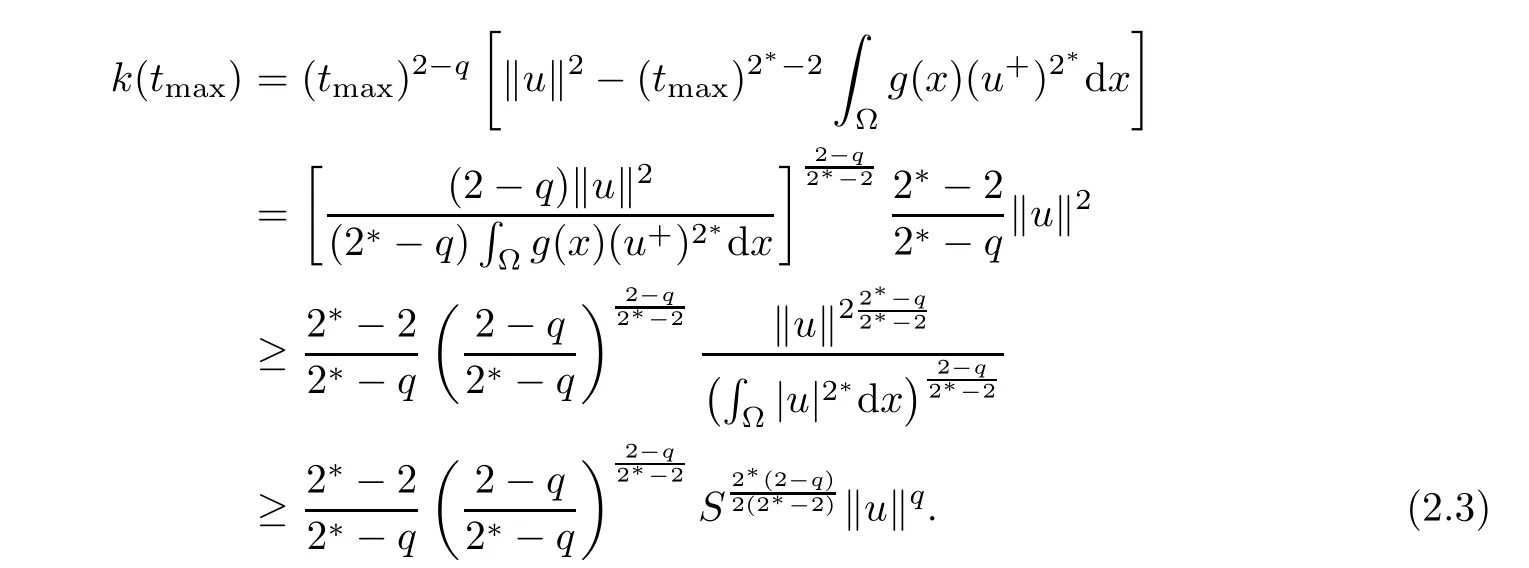
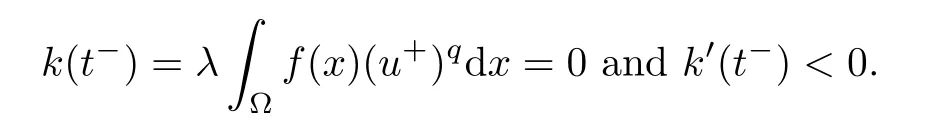
Then,we have

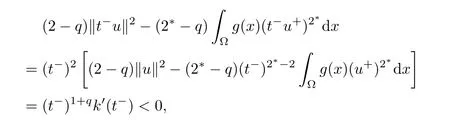
and

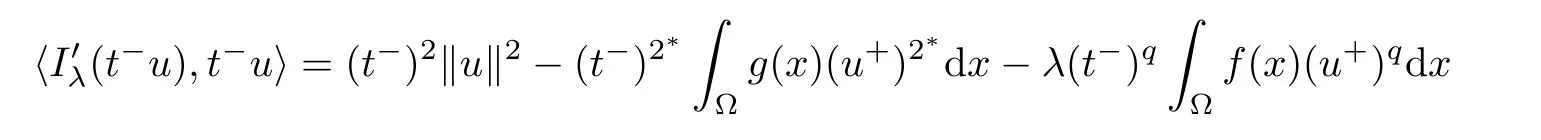
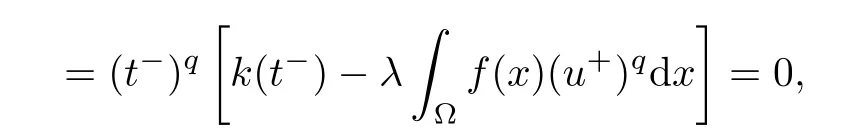
which implies that t?u∈N?.It follows that

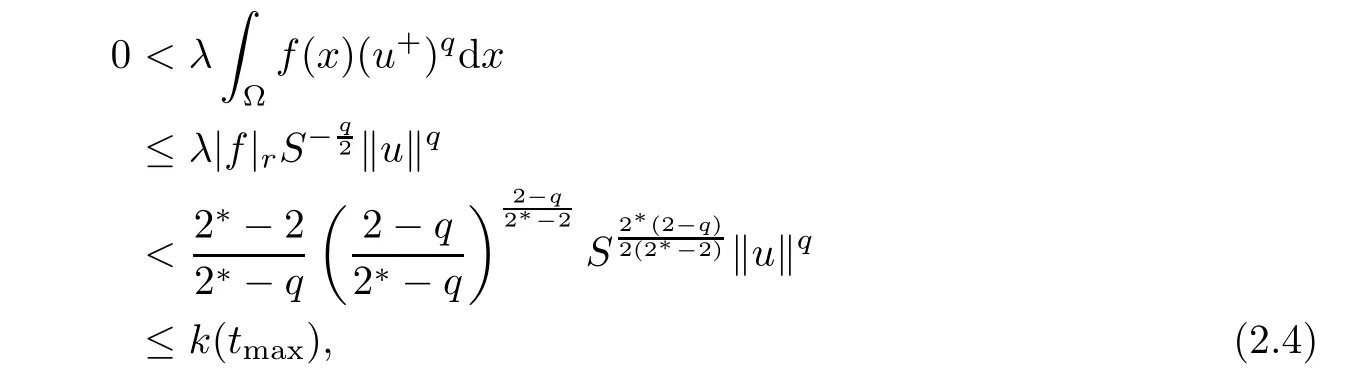
there exist unique t+and t?such that

for 0＜t+＜tmax＜t?.We have t+u∈N+,t?u∈N?and

for each t∈ [t+,t?],and Iλ(t+u)≤ Iλ(tu)for each t∈ [0,t+].Thus,

Next,we prove that N0={0}for all 0＜λ＜Λ.By contradiction,suppose that there exists u0∈N0with u0/=0.Obviously,u0∈N,it follows that

and

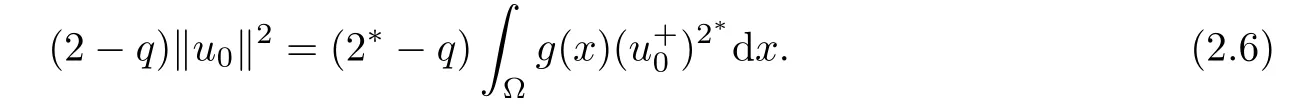
Consequently,

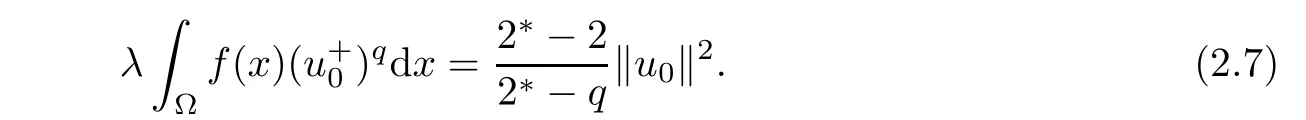
Then,according to(2.3),(2.4),(2.6),and(2.7),for all 0＜λ＜Λ,one has

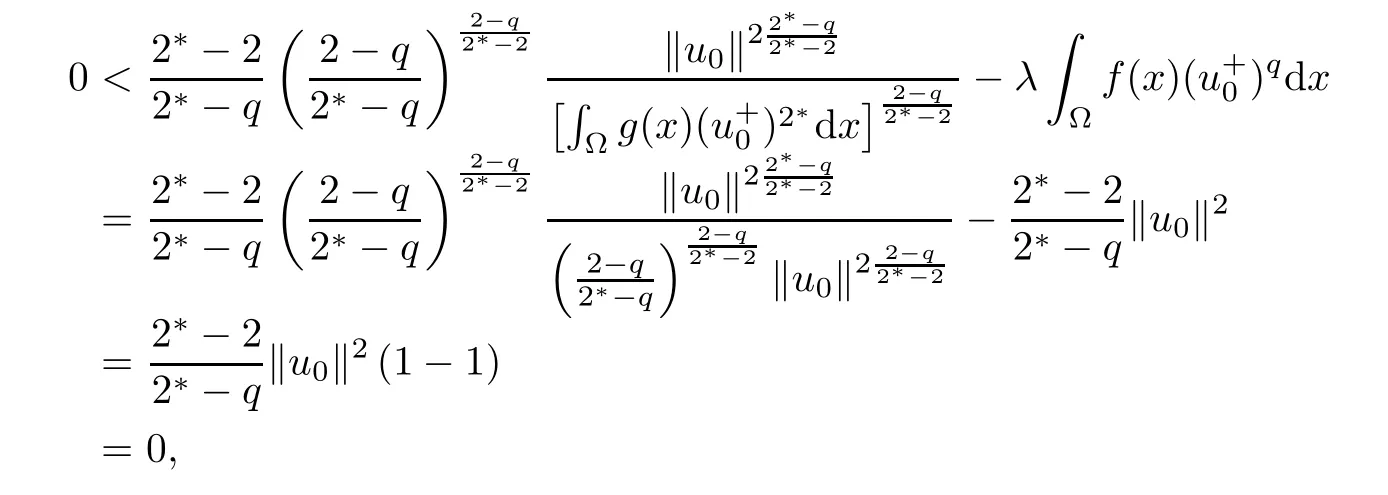
which is a contradiction.Thus,N0={0}for all 0＜λ＜Λ.

Finally,we prove that N?is a closed set for all 0＜λ＜Λ.Assume that{un}?N?such that un→u inas n→+∞,then we need prove that u∈N?.As un∈N?,from the definition of N?,one has

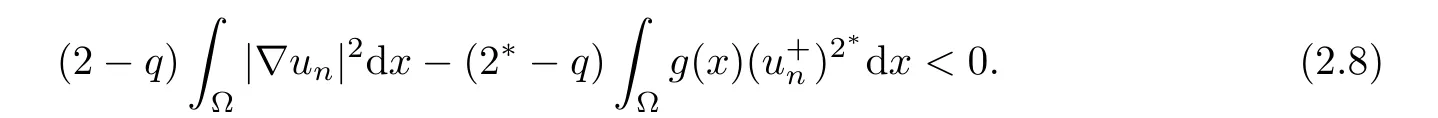
Consequently,as un→u inas n→+∞,it follows from(2.8)that

thus u∈N?∪N0.If u∈N0,because N0={0}for all λ ∈(0,Λ),one has u=0.However,from(2.8),byand(1.4),one has

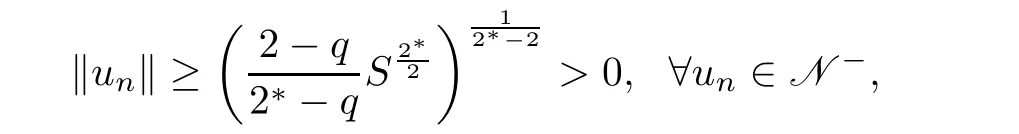
which contradicts u=0.Thus,u∈N?for all λ ∈(0,Λ).Therefore,N?is a closed set infor all λ ∈ (0,Λ).This completes the proof of Lemma 2.1.

Lemma 2.2Iλis coercive and bounded from below on N.

ProofBy the H?lder and Sobolev inequalities,one has

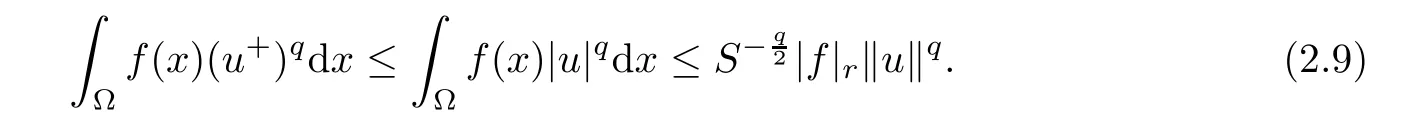
Consequently,for all u∈N,it follows from(2.9)that

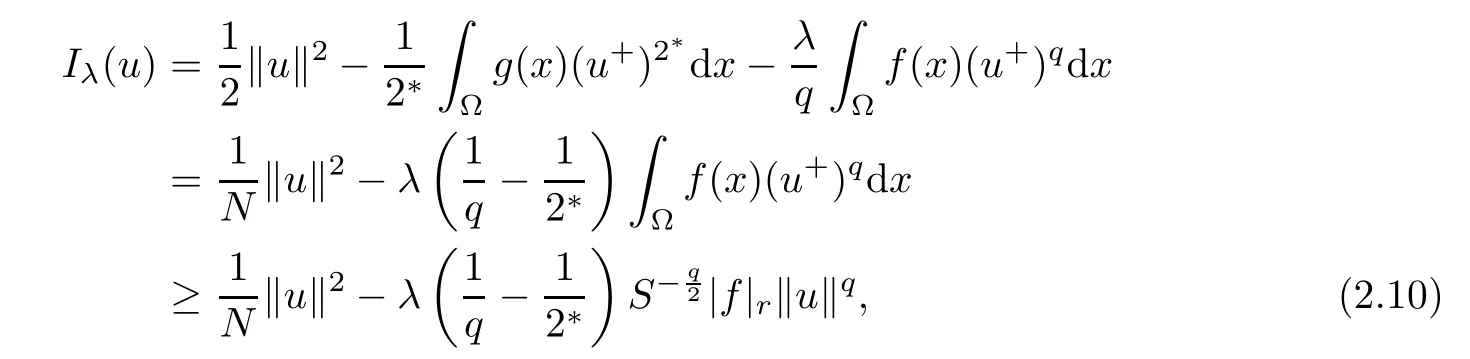
because 1＜ q＜ 2＜ 2?,which implies that Iλis coercive and bounded from below on N.Then,the proof of Lemma 2.2 is completed.

For 0＜λ＜Λ,by Lemma 2.1,one has N=N+∪N?∪{0}.Consequently,from Lemma 2.2,the following definitions are well defined

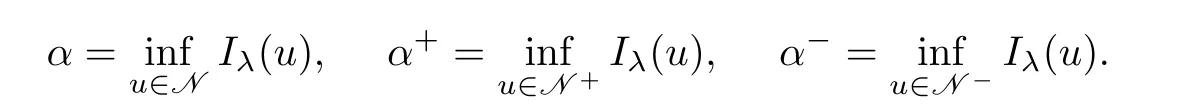
Lemma 2.3(i) α ≤ α+＜0 for all λ ∈(0,Λ);

(ii)there exists a positive constant c0depending on λ,N,S,and|f|r,such that α?≥ c0＞ 0 for all

Proof(i)For all u∈N+,we have

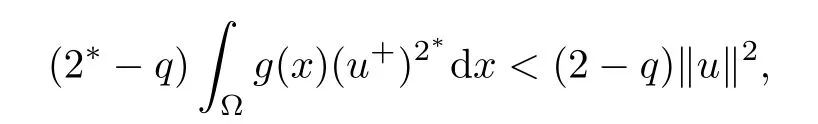
consequently,because of 1＜q＜2 and u/=0,it follows that

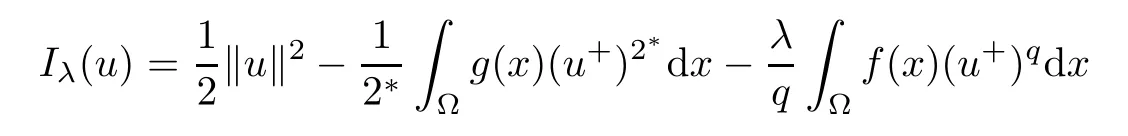
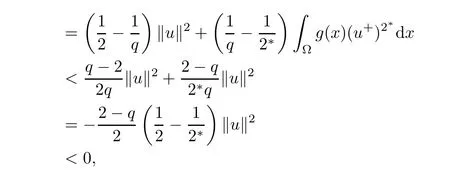
which implies that α+＜0.Thus,α ≤ α+＜0.

(ii)For u ∈ N?,byand the Sobolev embedding theorem,one has

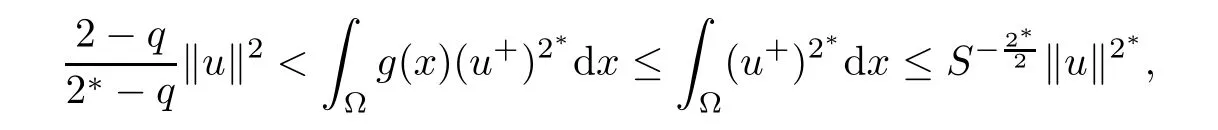
this implies that

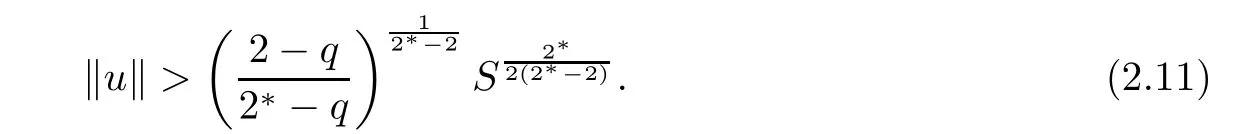
Consequently,from(2.10)and(2.11),we obtain

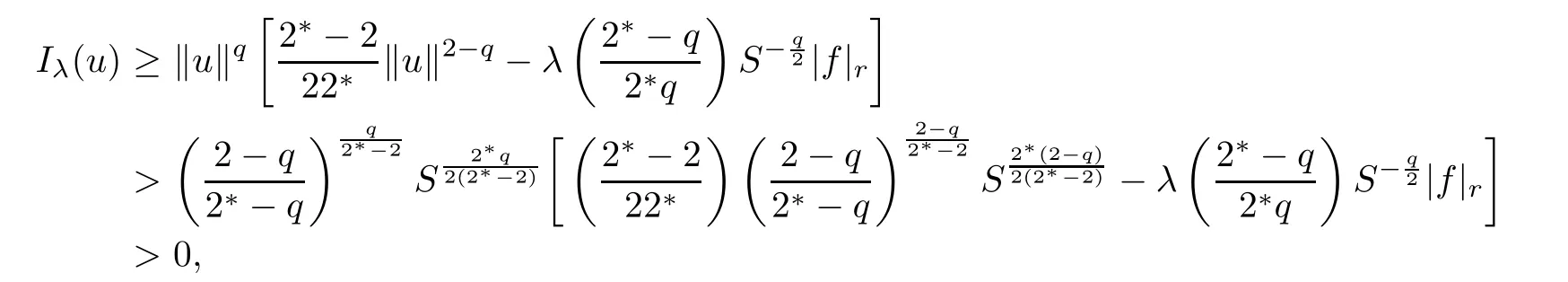
According to Theorem 2.3 in[6],we have the following lemma.

Lemma 2.4Suppose that u0is a local minimizer of Iλon N and 0＜ λ ＜ Λ,then

ProofSuppose that u0is a local minimizer of Iλon N,then u0is a solution of the optimization problem

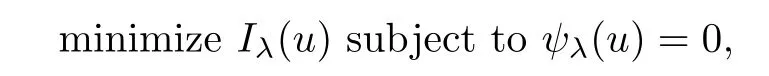
where

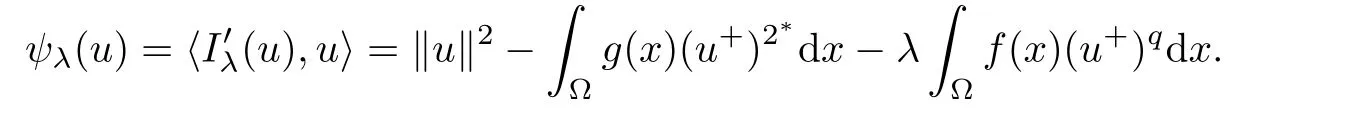
Furthermore,by the theory of Lagrange multipliers,there exists θ∈R such thatAs u0∈N,we get

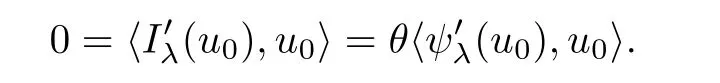
As 0＜ λ ＜ Λ,from Lemma 2.3,one has u0/∈N0.Consequently,θ=0 andinThis completes the proof of Lemma 2.4.

3 Existence of a Positive Ground State Solution

According to[28]or[38],we show the existence of a(PS)α-sequence and a(PS)α?-sequence in

Lemma 3.1(i)For all λ ∈ (0,Λ),there exists a(PS)α-sequence{un} ? N infor Iλ.

The proof of Lemma 3.1 is similar to the proof of Proposition 9 in[38];the reader can refer to[38].Now,we have the following proposition.

Proposition 3.2Let λ ∈ (0,Λ),then there exists uλ∈ N+such that

(i)Iλ(uλ)= α = α+;

(ii)uλis a positive ground state solution of problem(1.1).Moreover,one has Iλ(uλ)→ 0 and‖uλ‖ → 0 as λ → 0+.

ProofBy Lemma 3.1,there exists a minimizing sequence{un}?N such that

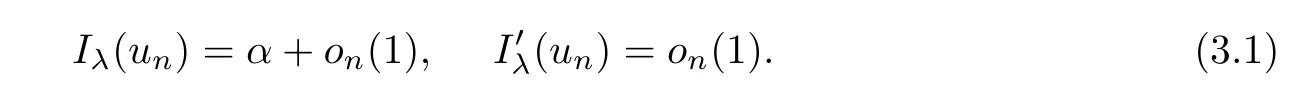
From Lemma 2.1,then Iλis coercive on N.It follows that{un}is bounded onGoing if necessary to a subsequence,still denoted by{un},there existssuch that

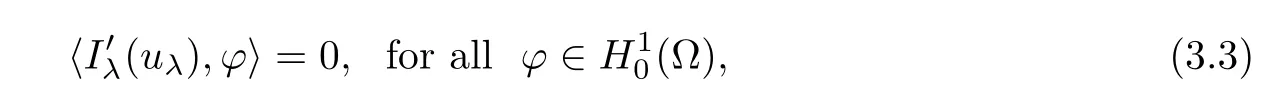
which implies that uλis a solution of problem(1.1).Particularly,choosing ? =uλin(3.3),one has uλ∈N.Because{un}?N,one has

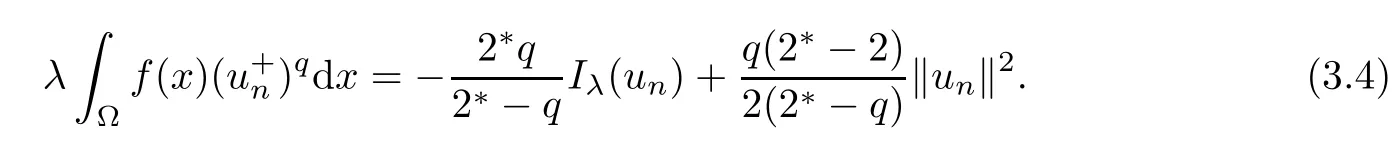
Letting n→∞in(3.4),with(3.1),(3.2),and the fact α＜0,we obtain

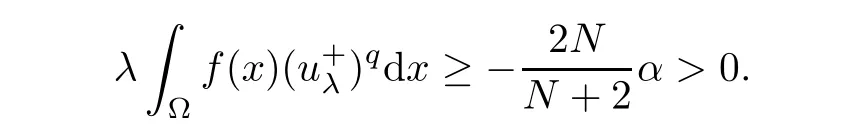
Therefore,uλ∈N is a nontrivial solution of problem(1.1).

Next,we prove that un→ uλstrongly inas n → ∞ and Iλ(uλ)= α.By Vitali’s theorem(see[32]pp:133),we claim that

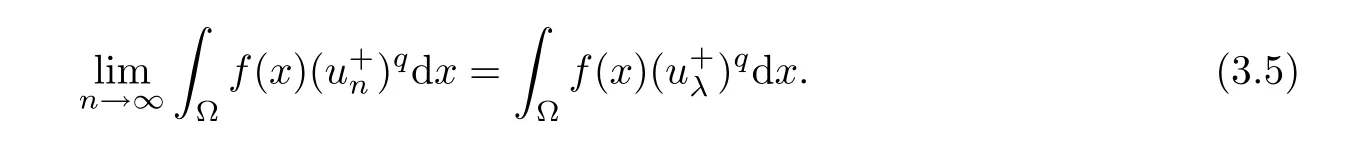
Indeed,we only need to prove thatis equi-absolutely-continuous.Noting that{un}is bounded,by the Sobolev embedding theorem,so there exists a constant C1＞ 0 such that|un|2? ≤ C1＜ ∞.By the H?lder inequality,for every ε＞ 0,setting δ＞ 0,when E?? with mesE＜δ,we have

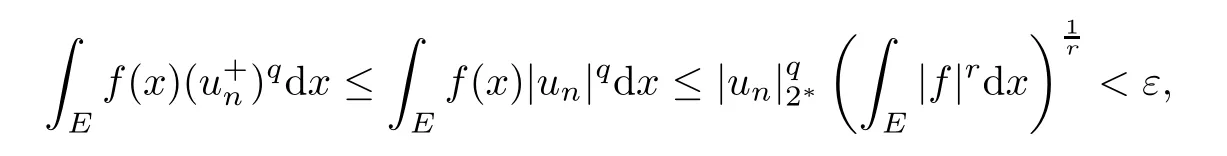
where the last inequality is from the absolutely-continuity ofRThus,our claim is proved to be true.Because of uλ∈N,by the Fatou Lemma,it follows from(3.5)that

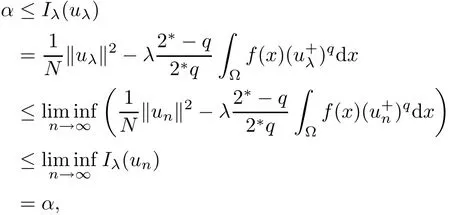
which implies that Iλ(uλ)= α andCombining with(3.2),un? uλas n → ∞ init shows that un→ uλstrongly inMoreover,we can claim that uλ∈ N+.Indeed,if uλ∈ N?,by Lemma 2.1,there exist uniqueandsuch thatBecause of

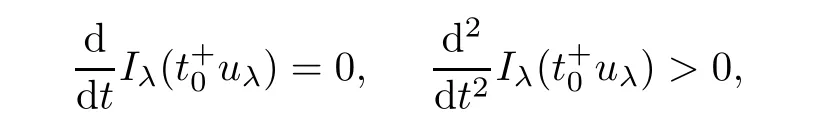
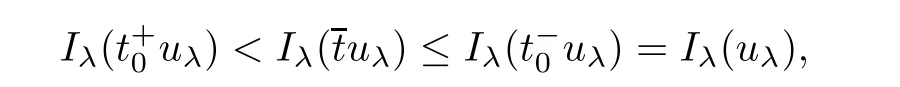
which is contradiction.Thus,according to Lemma 2.3(i),Iλ(uλ)= α,and uλ∈ N+,one has Iλ(uλ)= α = α+.

Finally,we prove that uλis a positive solution of problem(1.1).In fact,we choosein(3.3),one hasthis implies that=0,so uλ≥ 0.Consequently,as uλ0,by Lemma 2.4 and the strong maximum principle,then uλis a positive solution of problem(1.1).Therefore,uλis a positive ground state solution of problem(1.1).Moreover,from(2.10)and Lemma 2.4,we obtain

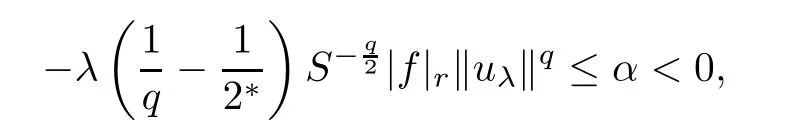
which implies that Iλ(uλ)= α → 0 as λ → 0+.As uλ∈ N+,from(2.9),one has

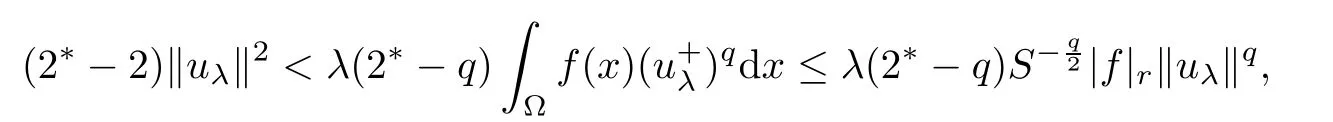
4 Proof of Theorem 1.2

In this part,we want to obtain k positive solutions of problem(1.1).To get rid of the constraining conditions of＜q＜2 and N ＞4 in[28],we try to obtain k positive solutions from the prolongation of the first solution uλin N?.Before proving Theorem 1.2,we give some important lemmas.

Lemma 4.1For allIλsatisfies the(PS)c-condition in

ProofLet{un}?be a(PS)c-sequence satisfying Iλ(un)=c+o(1)and=o(1).We claim that{un}is bounded inIn fact,for n large enough,one has

which implies that{un}is bounded inSo,our claim is true.Therefore,‖un‖ is bounded.Set vn=un? u?.By Brézis-Lieb’s Lemma,we have

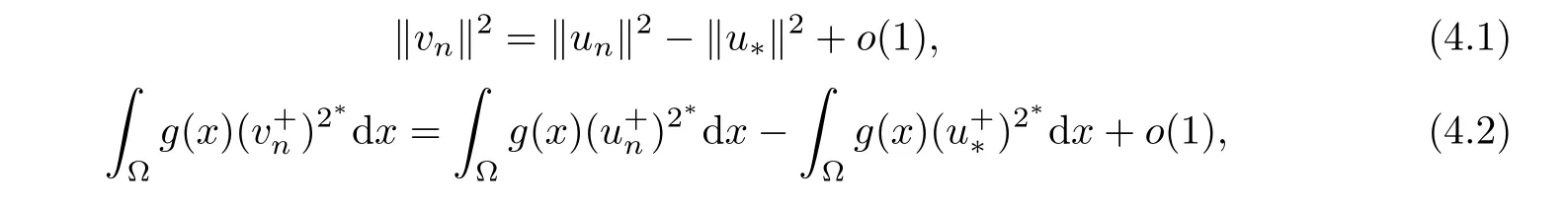
consequently,from(3.5),one has

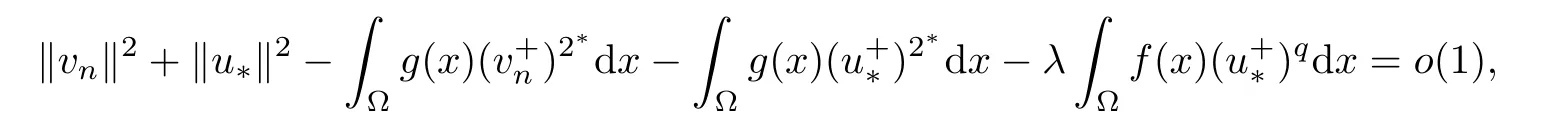
and

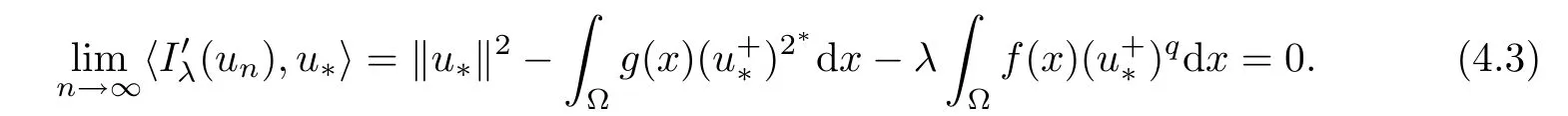
Now,we can assume that

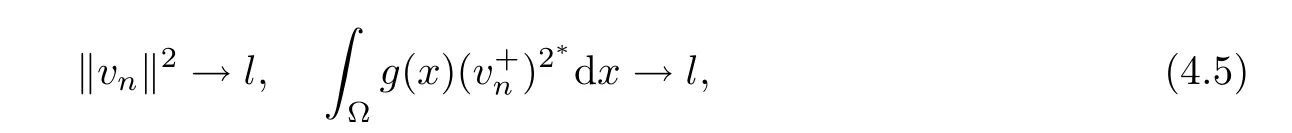
as n→∞.Applying the Sobolev inequality,one obtains

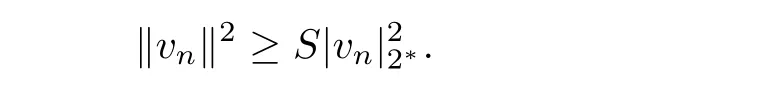
Then,l≥Sl22?,which implies that either l=0 or l≥ SN2.If l≥ SN2,by(4.4)and(4.5),we have

which is contradicts the definition of c.Therefore,l=0 and un→ u?strongly inThis completes the proof of Lemma 4.1.

We consider the following critical exponent problem

Associated with(4.6),we consider the energy functional I∞inthat is

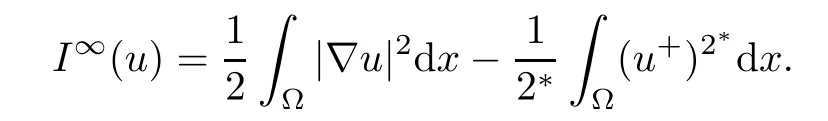
Now,following the methods of[5],let ηi∈be a radially symmetric function such that 0 ≤ ηi≤ 1,|?ηi|≤ C and for 1 ≤ i≤ k,we define

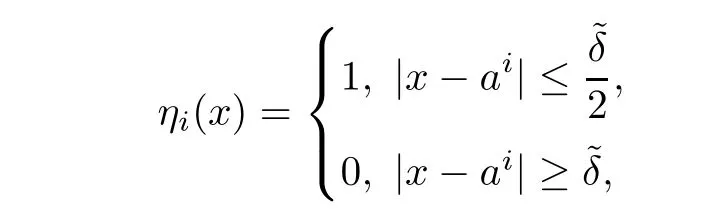
and

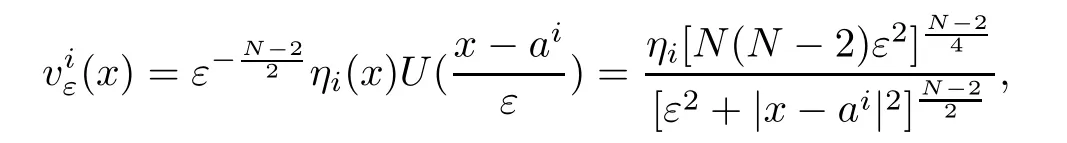
where U(x)is defined as(1.6).

Lemma 4.2Suppose that(f),(g),andhold,then

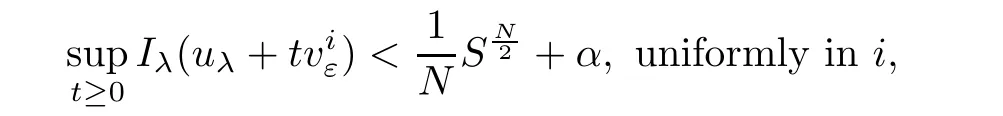
where 1≤i≤k.

ProofAccording to[4]or[16],we can easy to obtain the following classical results

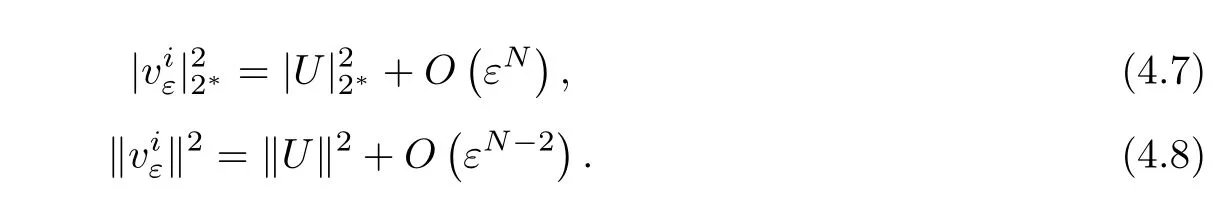
Moreover,one has

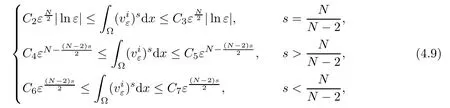
where Cl＞0(l=2,3,4,5,6,7)are positive constants.As uλis a positive solution of problem(1.1),one has

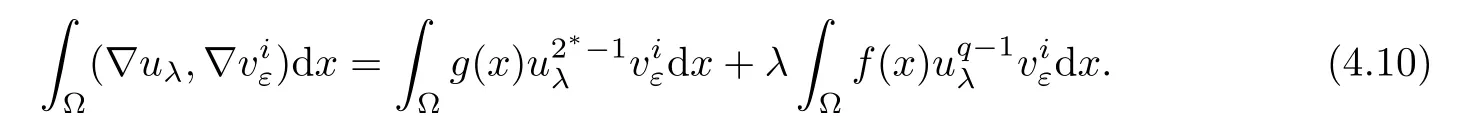
Moreover,by a standard method,we get uλ∈ C1(?,R+)and there exists a positive constant C8(C8independent of x)such that uλ＜ C8.Now,we give the following two elementary inequalities:

For any m＞2,there exists a positive constant C9=C9(m)such that

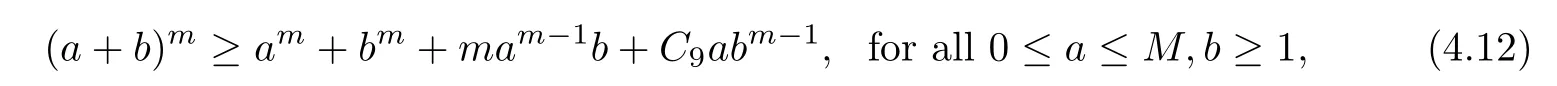
where M＞0 is a positive constant.

Then,combining with(4.10),(4.12)and(4.11),we easily obtain

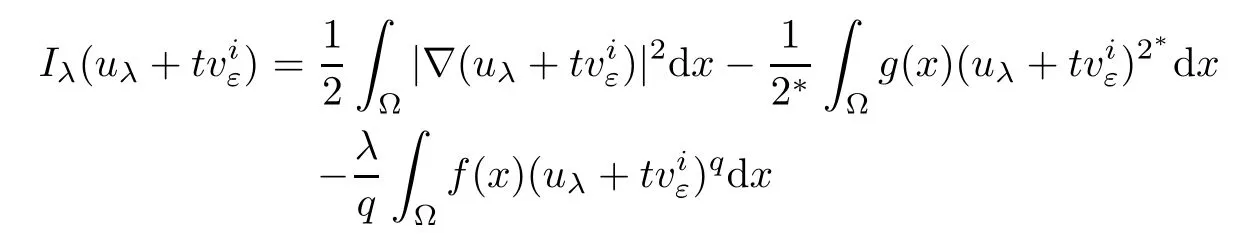
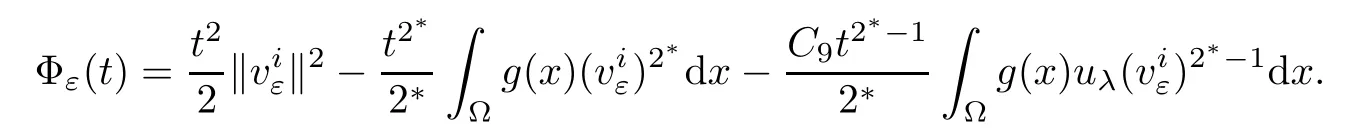
Notice that Φε(0)=0,uniformly for all ε.On the one hand,whenone hasThus,we have

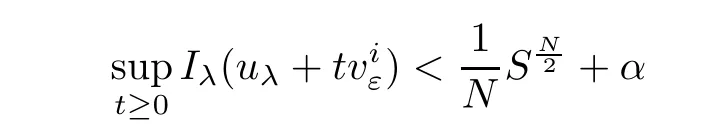
uniformly in i.On the other hand,whenthenand it attains for some tε＞0.So,there exist two constantssuch that T0＜tε＜T0.In fact,fromuniformly for all ε,we choosethen there exists T0＞0 such that

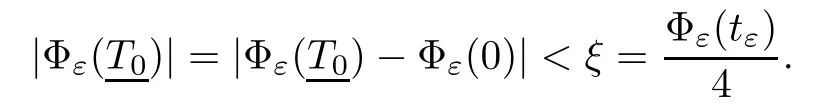
According to the monotonicity of Φεnear t=0,we have tε＞ T0.Similarly,we can obtainLet

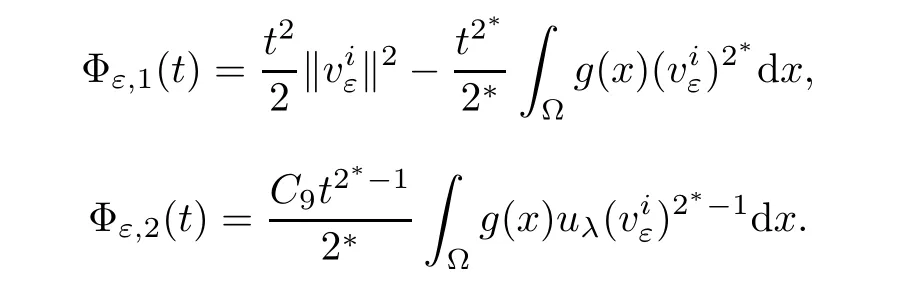
Then,we have

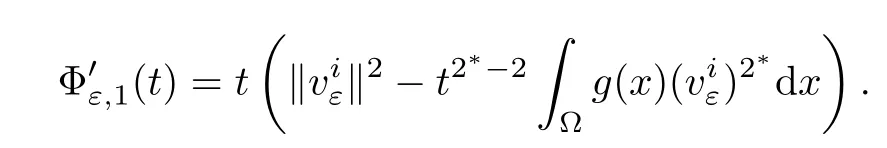
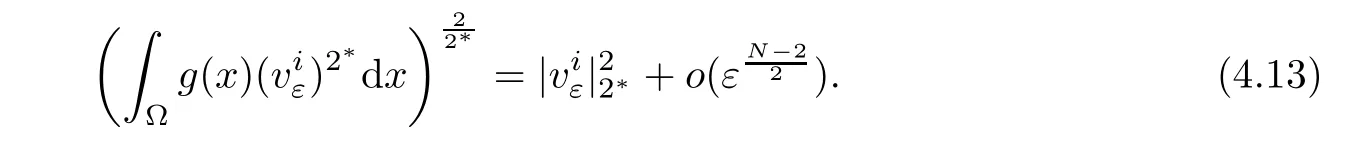
In fact,for all ε＞ 0,it follows that

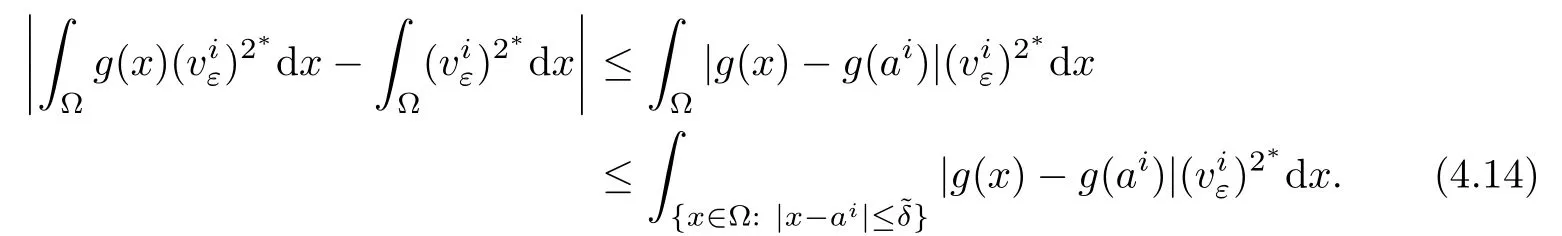
When ε＞ 0 small enough,for δ＞ ε12,it follows from(4.14),(g),andthat

where cN=[N(N?2)]N2,and C,C′＞ 0 are constants.Consequently,one has

which implies that

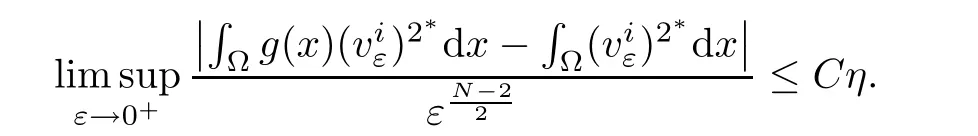
Then,from the arbitrariness of η,we obtain(4.13).Combining with(4.7)and(4.13),one has

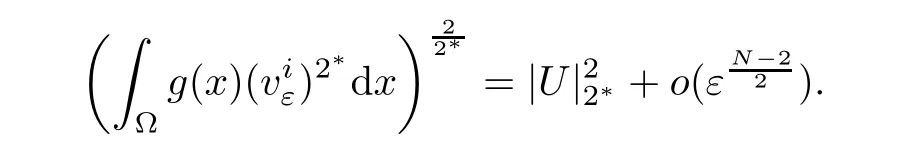
Consequently,from(4.8),it follows that

thus

and from(4.9),one obtains

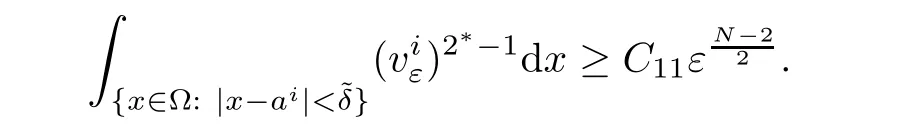
Consequently,it follows thatTherefore,

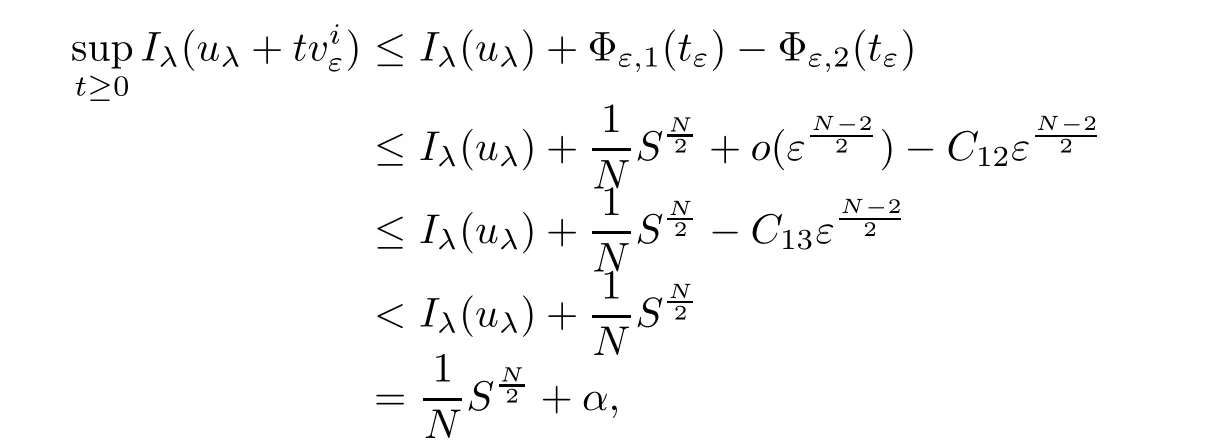
where C13＞0 is a constant and 1≤i≤k.

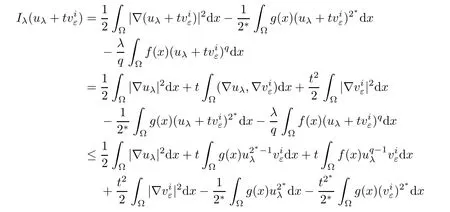
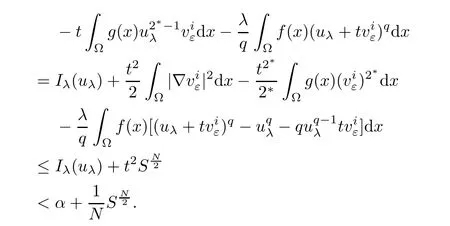
This completes the proof of Lemma 4.2.

According to[36],we have the following lemma.

Lemma 4.3For any 1≤i≤k,there existssuch thatN?for all λ ∈(0,Λ).Moreover,

ProofAccording to Lemma 2.1,there exists u∈ H10(?){0},consequently,there exists unique t?(u)＞ 0 such that t?(u)u ∈ N?.Set

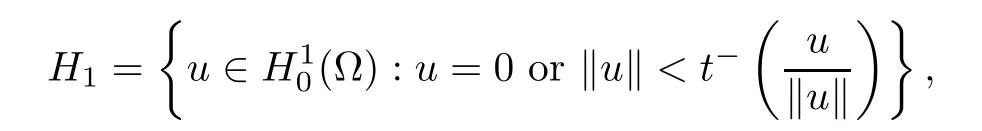
and

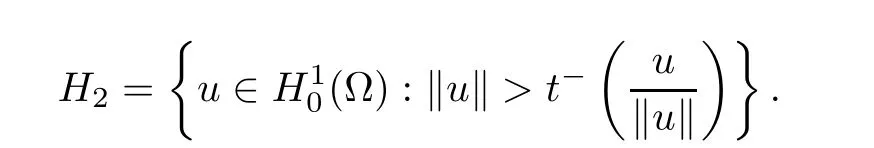
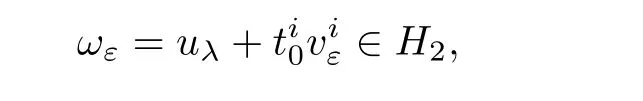
for ε ＞ 0 small.Indeed,from(4.10),(4.8),and(4.9),one has

This completes the proof of Lemma 4.3.

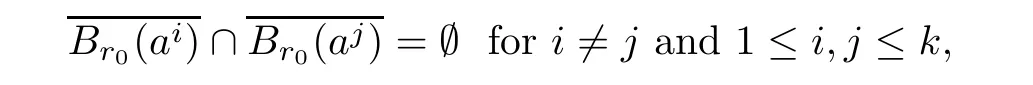
where χ:RN→RN

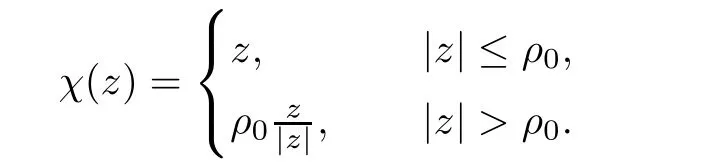
Lemma 4.4For any 1≤i≤k,thenMoreover,there exists ε0＞0 such that for all 0＜ ε＜ ε0,thenfor each 1≤i≤k.

ProofAccording to the definition of φ,we have

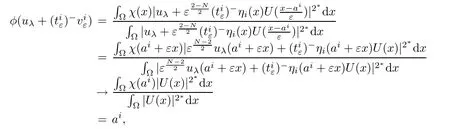
as ε→0+.This implies that there exists ε0＞0 such thatfor any 0＜ ε＜ ε0and each 1≤ i≤k.Then,the proof of Lemma 4.4 is completed.

For each 1≤i≤k,we define

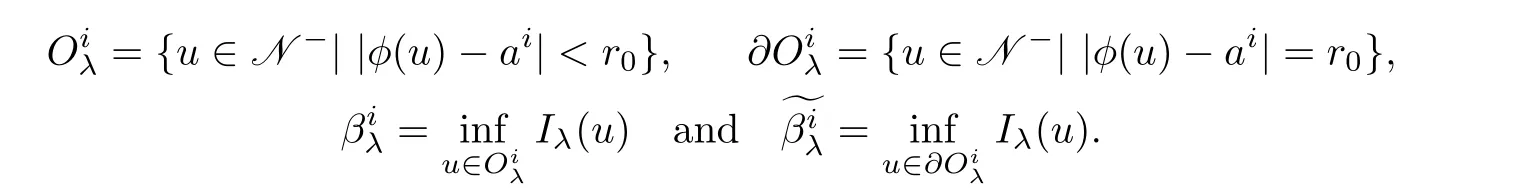
Lemma 4.5For all cIλsatisfies the(PS)c-condition in

ProofAssuming the contrary,we can suppose that there exists a sequence{un}?N0such thatand

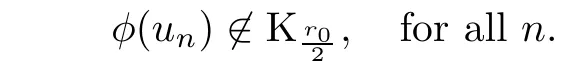
Then,I∞has a(PS)-sequence{un}in(see[24]).It follows from Lemma 2.2 that there exist a subsequence{un}and u0∈such that un? u0weakly in H10(?).Because? is a bounded domain,is not achieved.Applying the Palais-Smale Decomposition Lemma(see Theorem 3.1 in Struwe[34]),there exist two sequences{zn}? ?,{Rn}?R+,z0∈?,and a positive solution v0∈H1(RN)of the critical problem(1.6)with I∞(v0)=1NSN2such that zn→z0,Rn→∞as n→∞and

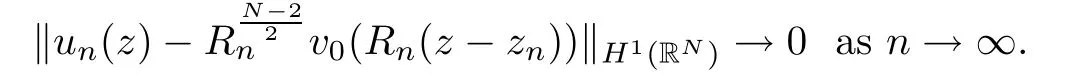
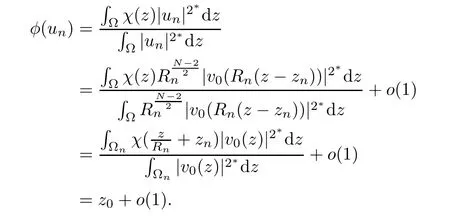
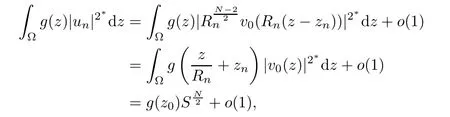
Lemma 4.6There existssuch that if 0＜λ＜Λ?and u∈N?withis given in Lemma 4.5),then we have φ(u) ∈

ProofSimilar to Lemma 2.1,then there is a unique positive number

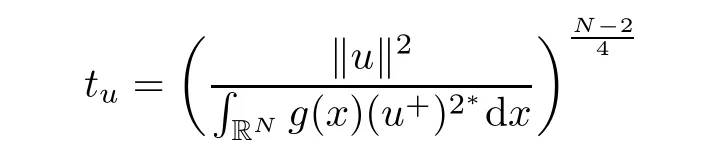
such that tuu∈N0.Now,we want to prove that tu＜C14for some constant C14＞0(independent of u and λ).From(2.11),if u ∈ N?,then

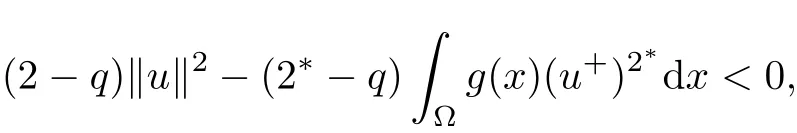
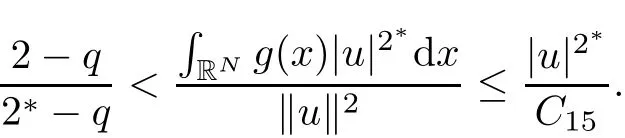
Thus,tu＜C14for some constant C14＞0.Thus,we have

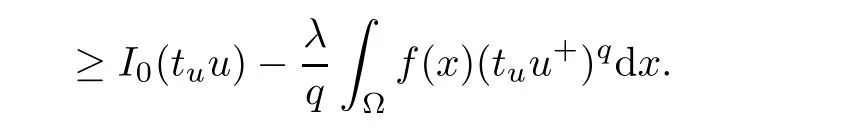
From the above inequality,we deduce that

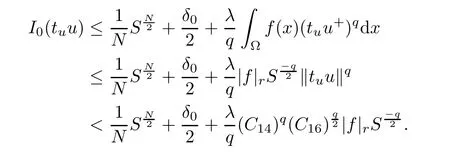
for 0＜ λ ＜ Λ?.Consequently,by Lemma 4.5,it follows that

for any 0＜ λ ＜ Λ?.The proof of Lemma 4.6 is completed.

From the above lemma,one has

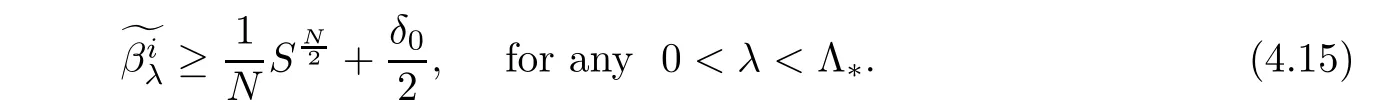
By Lemma 4.3,we have

Lemma 4.7For u∈,then there exist τ＞0 and a differentiable functionalsuch that ζ(0)=1,ζ(v)(u?v)∈for any v∈B(0;τ),and

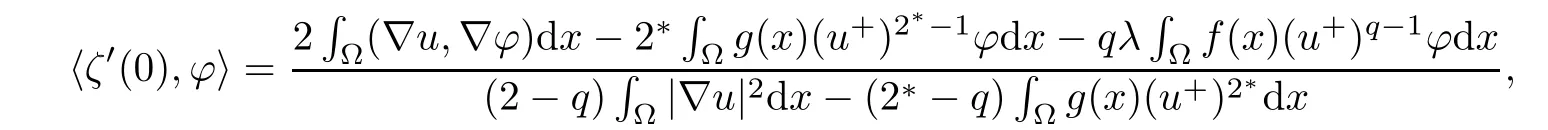
ProofThe proof is almost the same as in[10]or[38].For each u∈,define a function Fu:R×→R,given by

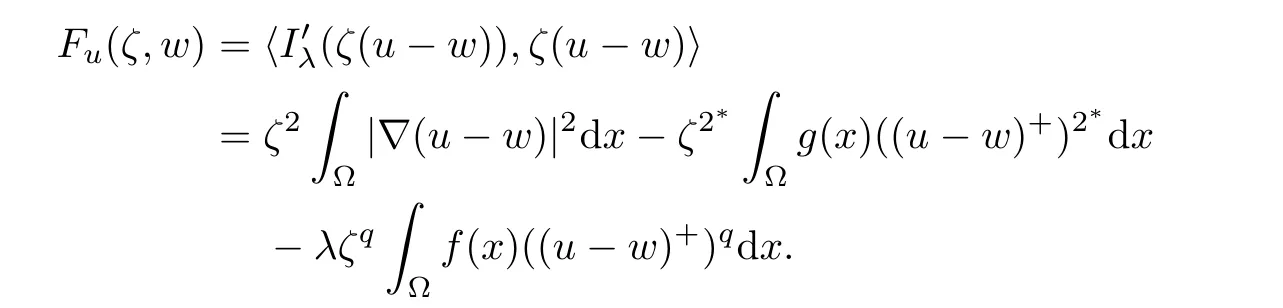
Then,Fu(1,0)=〉=0 and

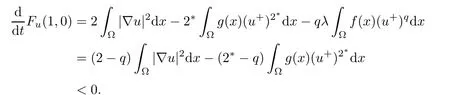
According to the implicit function theorem,there exist τ＞ 0 and a differentiable functionsuch that ζ(0)=1,

and

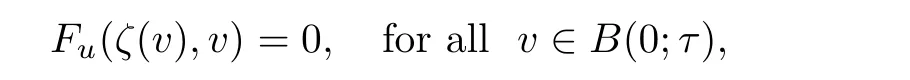
which is equivalent to

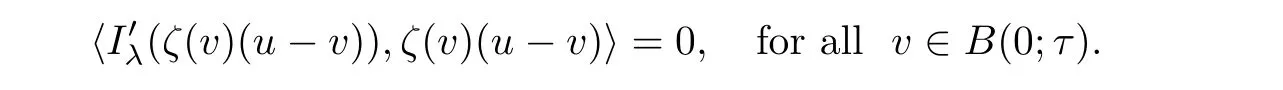
Lemma 4.8For each 1 ≤ i≤ k,λ ∈ (0,Λ?),there is ainfor Iλ.

ProofFor each 1≤i≤k,by(4.15)and(4.16),we obtain

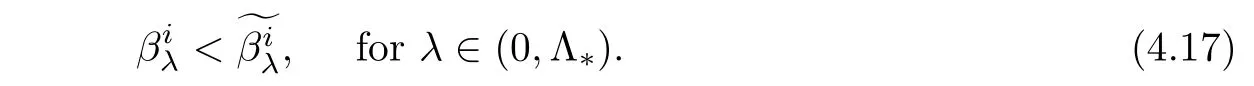
From(4.17),we may assume thatfor sufficiently large n.By Lemma 4.7,there exist a＞ 0 and a differentiable functionalsuch that=1,for anyLet vσ=σv with‖v‖=1 andThen,andFrom(4.18)and by the mean value theorem,as σ → 0,we obtain

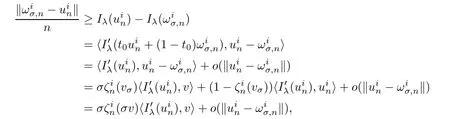
where t0∈ (0,1)is a constant and

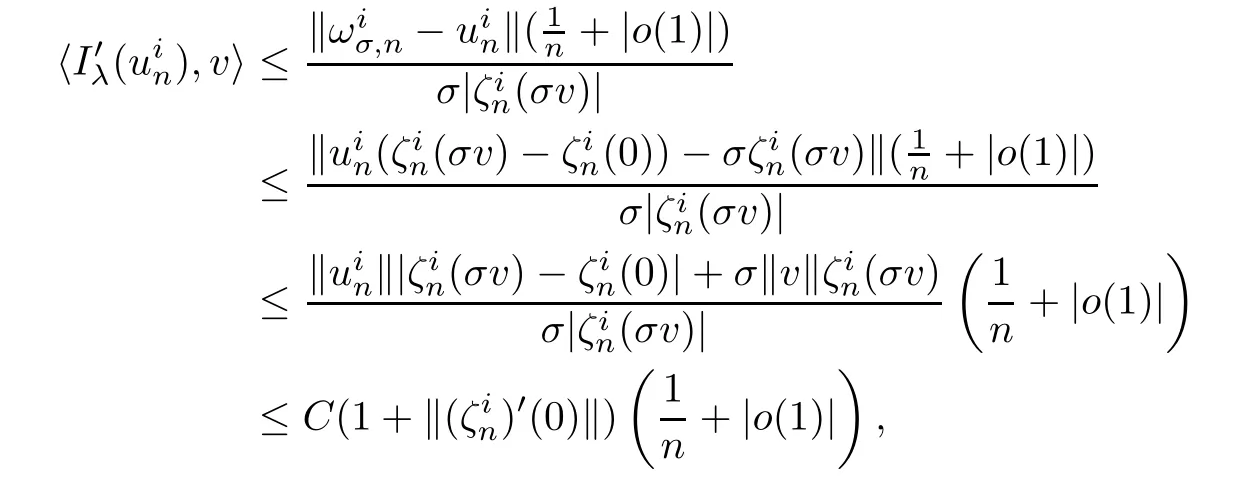
as σ →0.Hence,

where o(1)→ 0 as σ → 0.From Lemma 4.7,then there exists a positive constant M0such thatfor all n and i.Then,strongly inas n→∞.This completes the proof of Lemma 4.8.

Proof of Theorem 1.2By Lemma 4.8,there exists a(PS)βλi-sequence{un}?infor Iλand each 1 ≤ i≤ k.As Iλsatisfies the(PS)β-condition forfrom(4.16),then Iλhas at least k critical points in N?for 0＜ λ ＜ Λ?.It follows that problem(1.1)has k nonnegative solutions inApplying the strong maximum principle,problem(1.1)has at least k positive solutions.Combining with Proposition 3.2,we complete the proof of Theorem 1.2.

[1]Ambrosetti A,Azorero J G,Peral I.Elliptic variational problems in RNwith critical growth.J DiffEqu,2000,168:10–32.

[2]Ambrosetti A,Brézis H,Cerami G.Combined effects of concave and convex nonlinearities in some elliptic problems.J Funct Anal,1994,122:519–543

[3]Bahri A,Li Y Y.On a min-max procedure for the existence of a positive solution for certain scalar field equations in RN.Rev Mat Iberoam,1990,6:1–15

[4]Brézis H,Nirenberg L.Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents.Comm Pure Appl Math,1983,36:437–477

[5]Brézis H,Nirenberg L.A minimization problem with critical exponent and nonzero data//Symmetry in Nature.Scuola Normale Superiore Pisa,1989,I:129–140

[6]Brown K J,Zhang Y P.The Nehari manifold for a semilinear elliptic problem with a sign-changing weight function.J DiffEqu,2003,193:481–499

[7]Cao D M,Chabrowski J.Multiple solutions of nonhomogeneous elliptic equation with critical nonlinearity.DiffInteg Equ,1997,10:797–814

[8]Cao D M,Li G B,Zhou H S.Multiple solution for nonhomogeneous elliptic with critical sobolev exponent.Proc Roy Soc Edinburgh Sect A,1994,124:1177–1191

[9]Cao D M,Peng S J,Yan S S.In finitely many solutions for p-Laplacian equation involving critical Sobolev growth.J Funct Anal,2012,262:2861–2902

[10]Cao D M,Zhou H S.Multiple positive solutions of nonhomogeneous semilinear elliptic equations in RN.Proc Roy Soc Edinburgh Sect A,1996,126:443–463

[11]Cerami G,Zhong X X,Zou W M.On some nonlinear elliptic PDEs with Sobolev-Hardy critical exponents and a Li-Lin open problem.Calc Var Partial DiffEqu,2015,54:1793–1829

[12]Chen Y P,Chen J Q.Multiple positive solutions for a semilinear equation with critical exponent and prescribed singularity.Nonlinear Anal,2016,130:121–137

[13]Clapp M,del Pino M,Musso M.Multiple solutions for a non-homogeneous elliptic equation at the critical exponent.Proc Roy Soc Edinburgh Sect A,2004,134:69–87

[14]Drábek P,Huang Y X.Multiplicity of positive solutions for some quasilinear elliptic equation in RNwith critical Sobolev exponent.J DiffEqu,1997,140:106–132

[15]Du Y H,Guo Z M.Finite Morse index solutions of weighted elliptic equations and the critical exponents.Calc Var Partial DiffEqu,2015,54:3161–3181

[16]Ghoussoub N,Yuan C.Multiple solutions for quasilinear PDEs involving the critical Sobolev and Hardy exponents.Trans Amer Math Soc,2000,352:5703–5743

[17]Guo Z Y.Ground states for a nonlinear elliptic equation involving multiple Hardy-Sobolev rritical exponents.Adv Nonlinear Stud,2016,16:333–344

[18]Hirano N,Kim W S.Multiple existence of solutions for a nonhomogeneous elliptic problem with critical exponent on RN.J DiffEqu,2010,249:1799–1816

[19]Hirano N,Micheletti A M,Pistoia A.Multiple exitence of solutions for a nonhomogeneous elliptic problem with critical exponent on RN.Nonlinear Anal,2006,65:501–513

[20]Huang Y S.Multiple positive solutions of nonhomogeneous equations involving the p-Laplacian.Nonlinear Anal,2001,43:905–922

[21]Hsu T S,Lin H L.Three positive solutions for semilinear elliptic problems involving concave and convex nonlinearities.Proc Roy Soc Edinburgh Sect A,2012,142:115–135

[22]Korman P.On uniqueness of positive solutions for a class of semilinear equations.Discrete Contin Dyn Syst,2002,8:865–871

[23]Lan Y Y,Tand C L.Perturbation methods in semilinear elliptic problems involving critical Hardy-Sobolev exponent.Acta Mathematica Scientia,2014,34B:703–712

[24]Li T X,Wu T F.Multiple positive solutions for a Dirichlet problem involving critical Sobolev exponent.J Math Anal Appl,2010,369:245–257

[25]Liao F F,Yang M H,Tang C L.The existence a second positive solution of a class of elliptic equations with concave and convex nonlinearities with a critical exponent(Chinese).J Southwest Univ,2012,34:83–86

[26]Liao J F,Liu J,Zhang P,Tang C L.Existence of two positive solutions for a class of semilinear elliptic equations with singularity and critical exponent.Ann Pol Math,2016,116:273–292

[27]Liao J F,Liu J,Zhang P,Tang C L.Existence and multiplicity of positive solutions for a class of elliptic equations involving critical Sobolev exponents.RACSAM,2016,110:483–501

[28]Lin H L.Positive solutions for nonhomogeneous elliptic equations involving critical Sobolev exponent.Nonlinear Anal,2012,75:2660–2671

[29]Liu X Q,Liu J Q,Wang Z Q.Quasilinear elliptic equations with critical growth via perturbation method.J DiffEqu,2013,254:102–124

[30]Naito Y,Sato T.Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent.Ann Mat Pura Appl,2012,191:25–51

[31]Rabinowitz P H.Minimax methods in critical point theory with applications to differential equations//Regional Conference Series in Mathematics.American Mathematical Society,1986

[32]Rudin W.Real and complex analysis.New York,London etc:McGraw-Hill,1966

[33]Song Y Y,Wu X P,Tang C L.Multiple positive solutions for Robin problem involving critical weighted Hardy-Sobolev exponents with boundary singularities.J Math Anal Appl,2014,414:211–236

[34]Struwe M.Variational Methods(second edition).Berlin,Heidelberg:Springer-Verlag,1996

[35]Tang M.Exact multiplicity for semilinear elliptic Dirichlet problems involving concave and convex nonlinearities.Proc Roy Soc Edinburgh Sect A,2003,133:705–717

[36]Tarantello G.On nonhomogeneous elliptic equations involving critical Sobolev exponent.Ann Inst H Poincare Anal Non Lineaire,1992,9:281–304

[37]Tarantello G.Multiplicity results for an inhomogeneous Neumann problem with critical exponent.Manuscripta Math,1993,18:57–78

[38]Wu T F.On semilinear elliptic equation involving concave-convex nonlinearities and sign-changing weight function.J Math Anal Appl,2006,318:253–270

[39]Wu T F.On the semilinear elliptic equation involving critical exponent and sign-changing weight function.Commun Pure Appl Anal,2008,7:383–405

[40]Wu T F.Three positive solutions for Dirichlet problems involving critical Sobolev exponent and signchanging weight.J DiffEqu,2010,249:1549–1578

[41]Zhang J,Ma S W.In finitely many sign-changing solutions for the Brézis-Nirenberg problem involving Hardy potential.Acta Mathematica Scientia,2016,36B:527–536

[42]Zhang Z.On ground state solutions for quasilinear elliptic equations with a general nonlinearity in the critical growth.J Math Anal Appl,2013,401:232–241