Fukui Functions for the Temporary Anion Resonance States of Be-, Mg-,and Ca-
MORRISON Robert C.
Department of Chemistry, East Carolina University, Greenville, North Carolina 27858, USA.
1 lntroduction
Biological molecules can undergo radiation damage from interaction with low energy electrons1,2. A temporary anion state formed by an electron attaching to a low-lying orbital can affect the underlying electronic structure and lead to molecular dissociation. The effect of the attached electron has been examined using Fukui functions3.
Stabilization methods can be used in conjunction with standard electronic structure methods to determine the electronic structure of these temporary anion states4-8. The stable eigenvalues with respect to exponent scaling are determined by6,71) a minimum in the hyper-radius <r2>, 2) an inflection point in the energy νs scale factor λ, 3) an avoided crossing point between a stable and an unstable energy. Examples have been given using a model potential6, showing comparable results for the three methods.
Energies and wave functions of the resonance states of temporary anions can also be obtained through complex scaling of the Hamiltonian9. The electronic coordinates of the Hamiltonian are scaled by η = αeiθ. The resulting Hamiltonian matrix over symmetry adapted configurations is complex symmetric, non-Hermitian, giving complex energies

Εris the resonance energy and Γ is the width. Trajectories10-12in plots of Re(Ε) νs Im(Ε) as either α or θ is varied are used to determine Ε(η). Loops, kinks, or increased curvature in a trajectory indicate stabilities in Ε with respect to changing α or θ. Wave functions at these optimized values of α and θ are used to determine electron densities.
2 Theoretical background
The complex product, c-product13-16,

has been discussed and deemed appropriate17,18in analyzing complex wave functions for metastable states. In contrast to the ordinary scalar product
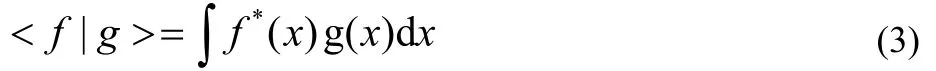
the f(x) is not complex conjugated in Eq.(2). The quantity x refers collectively to spatial and spin coordinates. This c-product form is used for calculating properties of the complex wave functions obtained from complex-scaled Hamiltonians.
The first-order reduced density matrix for these complex wave functions is obtained by
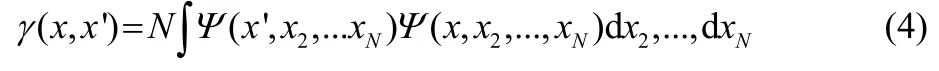
The wave function Ψ is not complex conjugated under the integrand. Expressing the wave function in terms of its real and imaginary parts
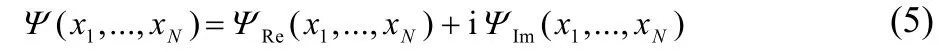
the reduced density matrix becomes,
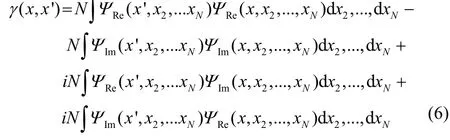
The first two terms constitute the real part of the density matrix, and the real part of the density is obtained as

By the normalization in Eq.(4) the electron density integrates to Ν electrons. The imaginary part integrates to zero.
The real parts of the electron densities are then used to determine the Fukui functions for examining the influence that a temporarily attached electron has on the underlying electronic structure. Fukui functions have been a valuable tool used in the interpretative aspects of density functional theory (DFT)19-21,and they have been important in the analysis of chemical reactivity. The Fukui function in terms of the density is defined by22

where Ν is the number of electrons, ν0refers to the external potential, ρ(r) is the electron density, and r represents the 3-dimensional spatial coordinates of the particle. Because of the derivative discontinuity23, the value of f(r) is evaluated above and below the integer value of Ν.

and

giving two different values of the Fukui function.
The Fukui function with superscript + is the derivative taken from above for adding an electron, and the Fukui function with superscript - is the derivative taken from below for losing an electron. This can be succinctly expressed as

The density in terms of the α and β spin components is

Fukui functions representing changes in the σ-spin electron density when the number of electrons with σ’ spin changes have previously been referred to as the spin Fukui functions24. The spin Fukui function can be written in terms of the corresponding densities25:
where σ and σ' represent α and β spins. For examplefβ+α(r)is the change in ρβ(r) when an α-spin electron is gained.
The working equations for calculating the Fukui functions from the densities of accurate configuration interaction (CI)wave functions are obtained by taking the difference between the densities

for a change in the number of electrons. The spin Fukui functions are determined by
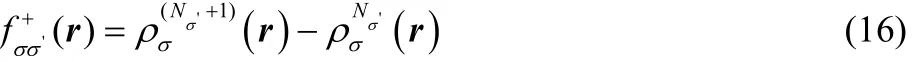
and
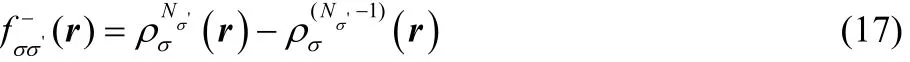
for a change in the number of electrons with σ' spin.
The integral of the Fukui function over its negative region(s)Ω is determined as26,

and

where

3 Method of calculation
Calculations were performed using the selected CI method27-30with up to quadruple excitations for both the neutral atom and its anion. The ARPACK31routines were used to find the lowest complex eigenvalues and corresponding eigenvectors of the complex symmetric matrices that resulted from complex scaling of the Hamiltonian. Our current version requires the Hamiltonian matrix to reside in memory, limiting the CI size to around 70000 configurations.
The orbital exponents of Slater type orbitals (STOs) were systematically optimized32for the anion of each atom and used both for the neutral atom and its anion, starting with initial self-consistent-field (SCF) calculations. In order to avoid collapse for the anion, a continuum remover potential33was added at the SCF level for the respective anions. The continuum remover was not included for the subsequent CI optimization of the remaining orbital exponents.
Accounting for electron correlation in open-shell systems requires more computational effort than in closed-shell systems of similar size. When adding an electron to a closed-shell system to form an open-shell, larger basis sets are needed for the open-shell system, with a larger number configurations, in order to perform calculations of comparable accuracy30. This problem has been partially offset in the current calculations by optimizing the basis orbitals for the open-shell anion, then using that basis set for the neutral closed-shell atom as well as for the open-shell anion. Therefore basis sets were optimized for the lowest2P state of Be-, the2P state of Mg-, and the2D state of Ca-, and these basis sets were also used for the neutral1S states of Be, Mg, and Ca, respectively.
As a test, a preliminary calculation was performed on Mg-Mg-using an STO basis set that was optimized for Mg for CI calculations of Mg, and an STO basis set that was optimized for Mg-for CI calculations of Mg-, resulting in Fukui functions that are visually identical to Fukui functions obtained by using the basis set optimized for Mg-in CI calculations on both Mgand Mg. Likewise the negativities IΩbetween the two basis sets are similar. The total energies differed by 0.008 a.u. (0.2 eV)which is significant when the energy differences of interest are less than 1.0 eV. All reported results are based on using the anion-optimized basis sets for both the neutral and the anion.
The optimized basis sets included up to 4f STOs for Be-, up to 5g STOs for Mg-and up to 6h STOs for Ca-. Nine even-tempered diffuse functions were added to each optimized basis set: nine 2p STOs for Be-, nine 3p STOs for Mg-, and nine 3d STOs for Ca-. Trial calculations were also performed using additional diffuse STOs of differing angular momentum quantum numbers without significant improvements in the results.
4 Results and discussion
The two2P resonance states of the Be-anion are examined both by scaling the orbital exponents of diffuse 2p orbitals in a stabilization method, and by complex rotation of the Hamiltonian. The2P resonance state of the Mg-anion and the2D resonance state of the Ca-anion are examined by complex rotation of the Hamiltonian.
4.1 Be-Be-
A stabilization calculation using the unscaled Hamiltonian was performed on Be-by scaling the nine even-tempered diffuse 2p functions by a scale factor λ. Fig.1 shows plots of ΔΕiνs λ for the 3 lowest energy levels of the2P states of Be-,referred to as CI1 through CI3. The energy above threshold,ΔΕi, is the eigenvalue difference
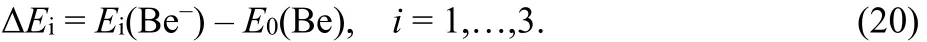
Ε0(Be) = -14.6645 a.u. There are two avoided crossings between CI1 and CI2, one near λ = 1.2 and the other near λ =3.2. These avoided crossings indicate stabilization at the resonance energies.
Fig.2 shows graphs of <r2> νs scale factor λ. The <r2> νs λ curve for CI1 in Fig.2a shows a minimum at λ = 1.0 near the first avoided crossing and in Fig.2b the <r2> curve for CI2 shows a minimum at λ = 3.2 near the second avoided crossing.
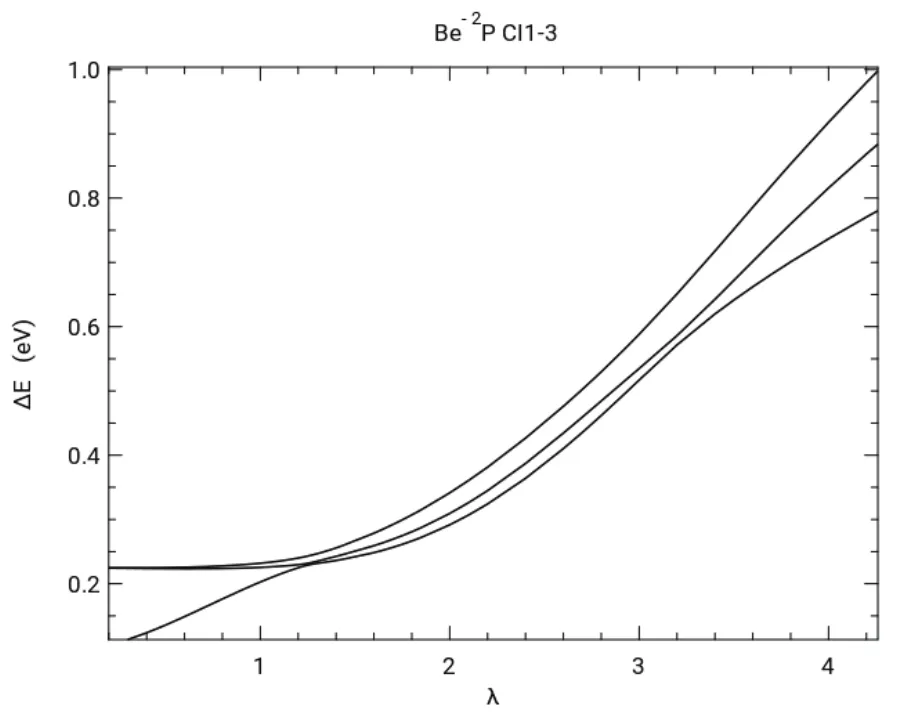
Fig.1 ΔE νs exponent scale factor for 3 energy states of Be-, Eq.(20).
The scaled diffuse STOs corresponding to the minima of<r2> for the two states were used to perform trajectory calculations using the complex-scaled Hamiltonian. The trajectories for the two states shown in Fig.3 illustrate the resonance points by a loop for resonance 1 in Fig.3a and the kink for resonance 2 in Fig.3b.
A calculation was also performed on resonance state 2 using the unscaled basis set. Although a trajectory similar to Fig.3b with a less prominent kink was observed, the value of <r2> was around 200000 a.u. in this unscaled STO basis set. A minimum in <r2> is an indication of a resonance state8. Using the unscaled basis set in an attempt to calculate resonance 2 did not produce a resonance state as indicated by the large value of<r2>. A plot of the density, not shown here, shows that it oscillates far into the continuum.
Values of the resonance energies are compared with other results34-36in Table 1. The present stabilization calculations were not analytically continued into the complex plane, but the numerical stabilization results in Table 1 were determined from the real wave functions at the <r2> minima. Most of the previous results include only one resonance state for Be-,except for ref.34. The resonance energy results reported here are similar to previous results.
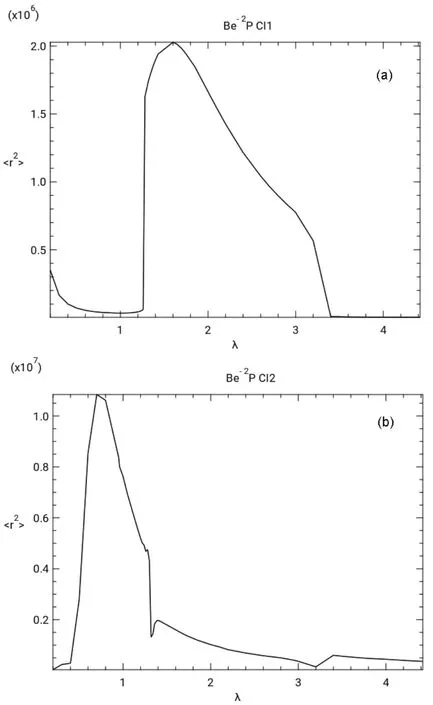
Fig.2 Values of
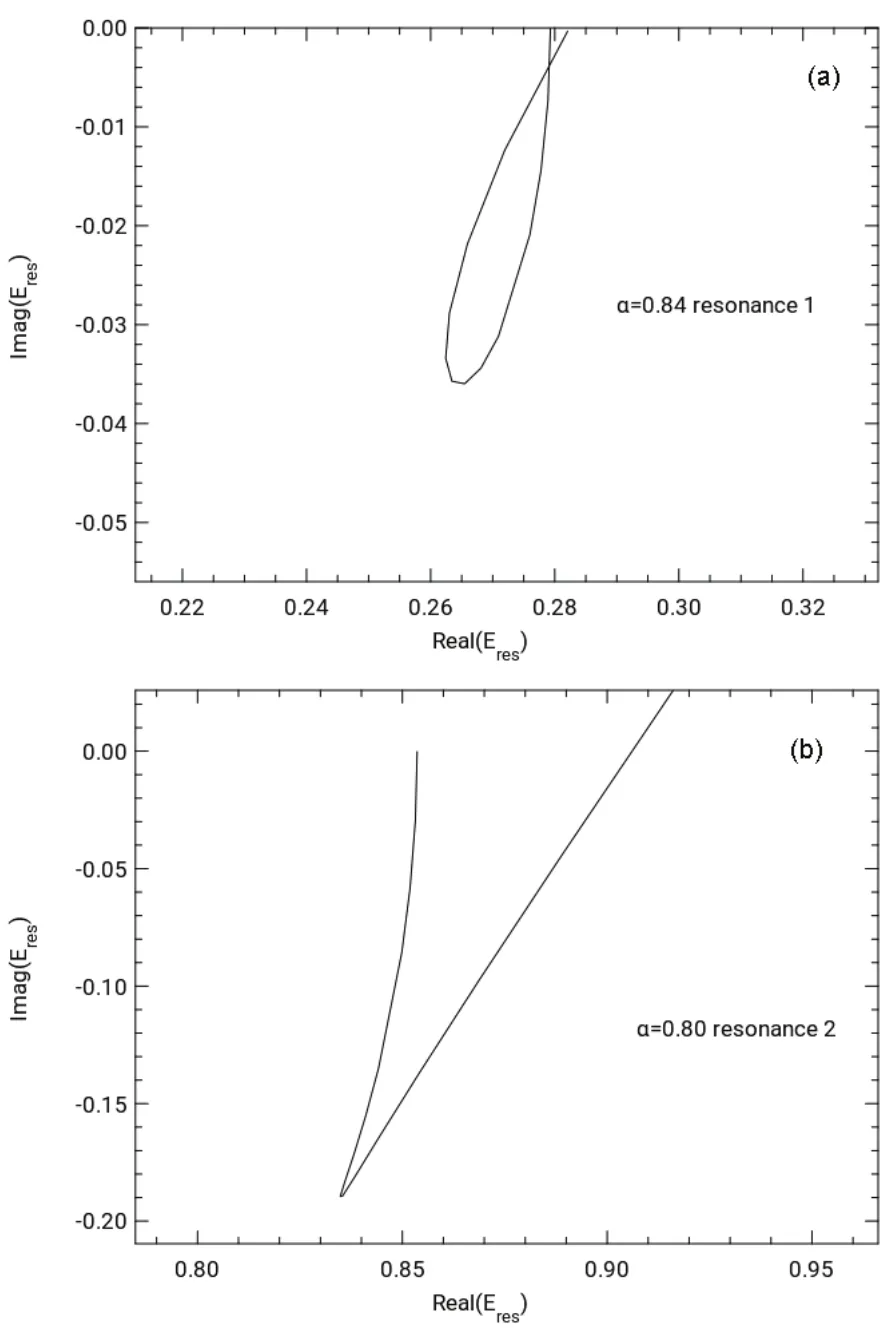
Fig.3 (a) θ trajectory for Be- resonance 1 with the optimized α value of 0.84; (b) θ trajectory for Be- resonance 2 with the optimized α value of 0.80.
As seen in Table 1 the <r2> values obtained from the real wave functions of the present stabilization calculations differ somewhat from those calculated from the complex wave functions obtained by the complex rotation of the Hamiltonian.This suggests that any properties calculated from these real wave functions may not be accurate.
The Fukui functions and electron densities for Be-aremultiplied by 4πr2to obtain the radial quantities. The (Ν +1)-electron densities have been included for reference when examining the Fukui functions and have been scaled to emphasize the valence region in the Fukui plots. The inner shell regions of the electron densities are off the scale in the Fukui function plots.

Table 1 Resonance energies (Er) and widths (Γr) in eV, and
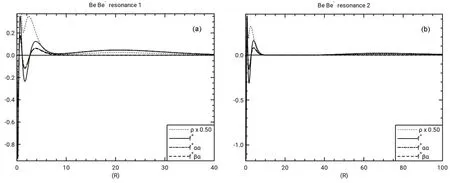
Fig.4 Radial Fukui function and radial density νs r in a.u.
The positive radial Fukui function for Be and its spin components are plotted in Fig.4 for the two resonance states of Be-. The radial Fukui function for resonance 1 has an outer peak near r = 20 a.u., in a position similar to the first outer peak in the radial density shown in Fig.2 of Venkatnathan et al.37.The f+ααclosely follows f+in the outer regions since the electron being added has α spin. The f+βαis near zero in the outer region, then shows both positive and negative values in the valence and inner shells. The f+βαfollows f+ααfairly closely in the valence and inner regions, more so for resonance 1 than resonance 2. This indicates that the outer, temporarily-attached electron effectively screens inner electrons with α spin as well as those with β spin. This effective screening of electrons with the same spin is supported by the magnitudes of I (f+βα) for Be in Table 2, which are similar to the magnitudes of IΩ(f+αα).Thus the screening of β-spin electrons by the temporarily attached α-spin electron is comparable to the screening of the α-spin electrons, so that the density of electrons of both spins is reduced in the inner region. Note that the resonance 2 value of IΩ(f+) = -0.620 in Table 2 has a magnitude that is larger than of IΩ(f+) = -0.456 for resonance 1 even though the resonance 2 temporary electron is further from the nucleus, indicated by the larger <r2> listed in Table 1.
4.2 Mg-Mg- and Ca-Ca-
Scaling the exponents of diffuse 3p orbitals for Mg-and diffuse 3d orbitals for Ca-did not produce the well-defined avoided crossings that are observed for the Be-resonance states.A non-systematic trial and error using <r2> and the total energy of the neutral was used to determine the even-tempered diffuse 3p STO basis functions for Mg-and the 3d STO basis functions for Ca-. The obtained energies are Ε0(Mg) = -200.0112 a.u.and Ε0(Ca) = -677.4501 a.u.
These basis sets were used to perform the trajectory calculations shown in Fig.5 using the method of complex rotation of the Hamiltonian. There is a lack of sharp kinks or loops as seen for Be-, so there is some arbitrariness in selecting the resonance point based on increasing curvature in the trajectory. Although this might lead to loss in accuracy, the resonance energy Εr= 0.24 eV and width Γ = 0.1 eV for Mgreported in Table 1 are in fair agreement with the experimental results38of Εr= 0.15 eV and width Γ = 0.14 eV, as well as with other theoretical calculations listed in Table 1. The calculated resonance energy Εr= 0.50 eV for Ca-is significantly lower than the experimental value of 1.1 eV, possibly due to takingthe difference of large values of the energies. But the calculated width Γ = 0.40 eV is comparable to the experimental width Γ =0.50 eV for Ca-39. The values of <r2> change only slightly over a broad range of the complex scaling parameters, so it is expected that the densities and corresponding Fukui functions will be fairly representative of the exact values.
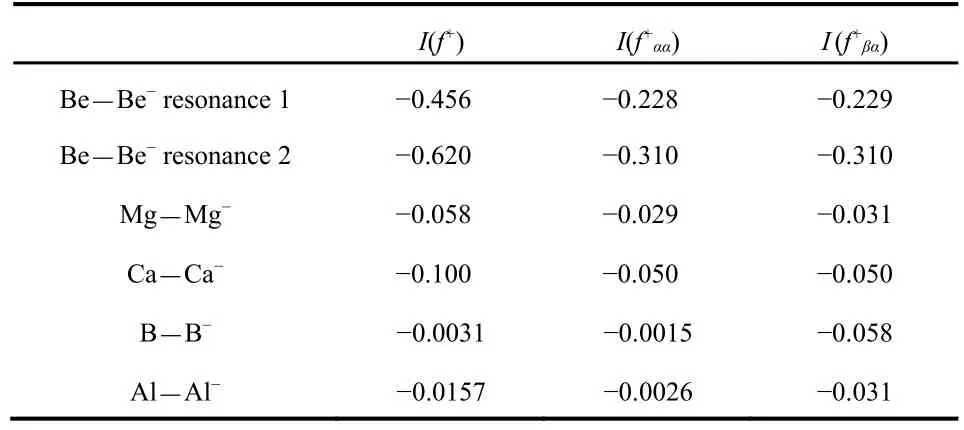
Table 2 Values of the negativity I for the positive Fukui functions obtained by adding an α-spin electron to the closed shell neutral atoms.
The Fukui functions for Mg and Ca shown if Fig.6 show an outer peak around r = 15.0-20.0 a.u. On this basis and the values of <r2>, the resonance electrons for Mg-and Ca-appear to be held more tightly than those in the resonance states for Be-.
All three atoms have f+βαthat track fairly closely with the corresponding f+ααin the valence and inner shell regions. By contrast the negative regions of f+βαfor B and Al, as seen in Fig.7, are much more dominant than the corresponding f+αα.The Fukui functions for B and Al show more shielding of the β electrons than the α electrons by the added α electron, a result attributed to pairing up of α and β electrons, while two α electrons are spatially separate in conformance with the Pauli Principle. This can also be seen in Table 2 where the magnitudes of IΩ(f+βα) for B and Al are about an order of magnitude larger than the corresponding magnitudes of IΩ(f+αα).
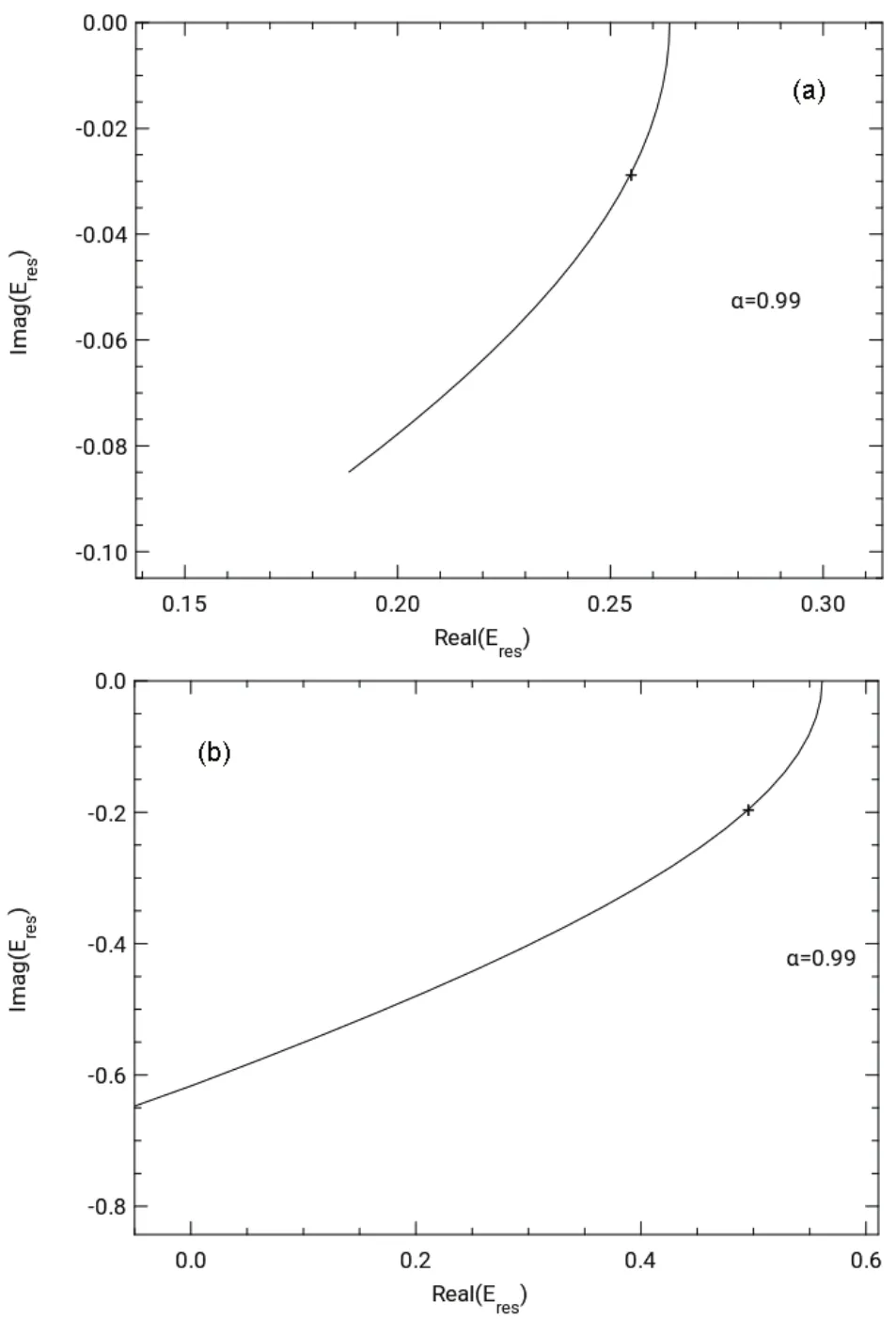
Fig.5 θ trajectory for (a) Mg-2P resonance and (b) Ca-2D resonance with the optimized α value of 0.99.
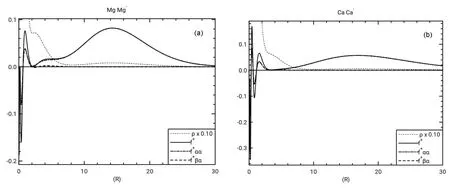
Fig.6 (a) Radial Fukui functions and electron density νs r in a.u. for Mg, Mg-, and radial density for Mg-;(b) radial Fukui function and radial density νs r in a.u. for Ca, Ca-, and radial density for Ca-.
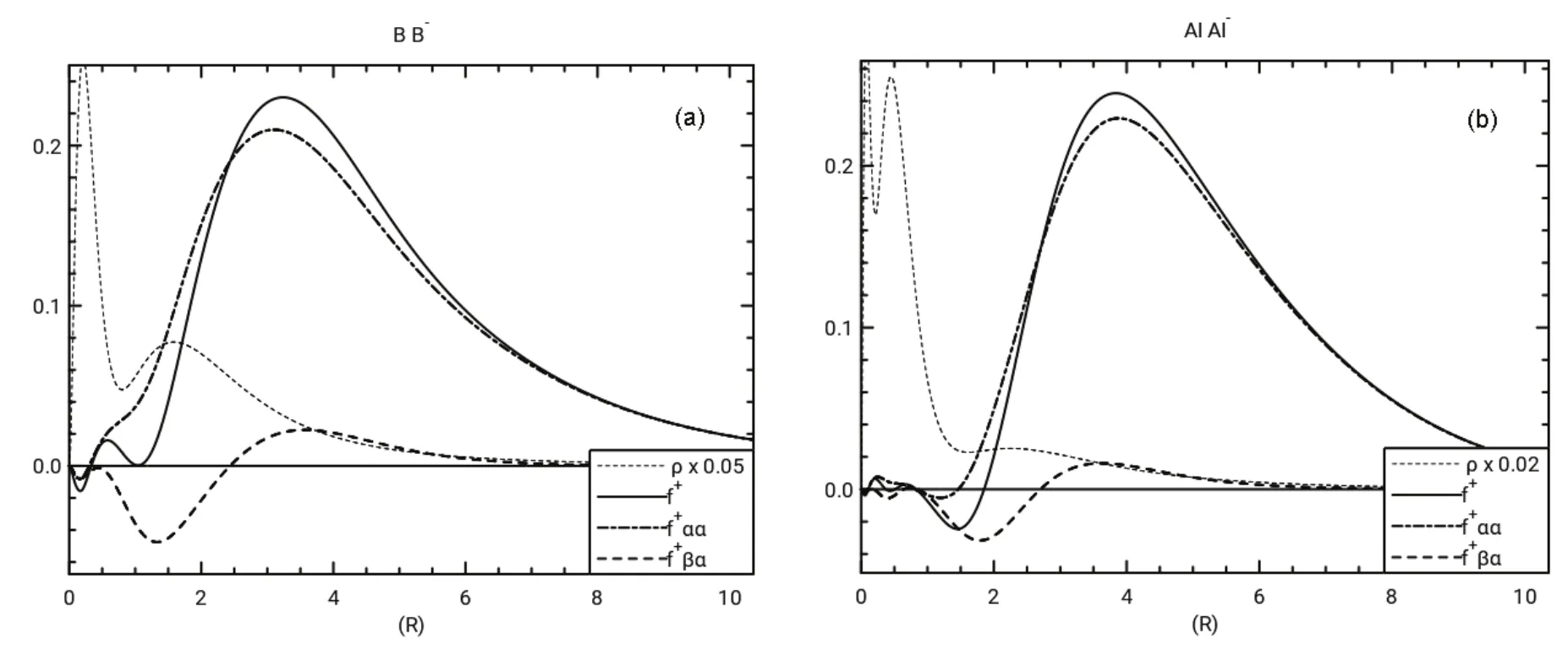
Fig.7 (a) Radial Fukui function and radial density νs r in a.u. for B, B-, and radial density for B-;(b) Radial Fukui function and radial density νs r in a.u. for Al, Al-, and radial density for Al-.
5 Remarks
Selected CI along with complex rotation of the Hamiltonian provides an effective means of examining temporary anion states. The c-product of the resulting complex wave functions can be used for obtaining real properties such as the electron density and the hyper-radius.
The magnitudes of the negativities IΩ(f+) appear to increase with increasing distance of the temporarily attached electron from the nucleus as illustrated by the values of <r2>. Negative regions of the positive Fukui functions in the valence and inner shells shown here for the temporary anion states demonstrate the sensitivity of the underlying electronic structure to a loosely attached electron. Even though the Fukui functions show that the attached electron has significant amplitude far from the nucleus, it also has sufficient amplitude in regions nearer the nucleus to provide screening in the valence and inner shells,reducing the electron density in those regions. The magnitudes of the negativities IΩ(f+) appear to increase with increasing distance of the electron from the nucleus as illustrated by the values of <r2>.
In contrast to the stable anions B-and Al-, the added α electron in a temporary anion effectively screens electrons with α spin as well as those with β spin in the temporary anion states of Be-, Mg-, and Ca-. In addition, the magnitudes of the negativities IΩ(f+) are somewhat higher for the temporary anion states of Be-, Mg-and Ca-than for the stable anions B-and Al-.
Outer electrons associated with resonance states have significant impact on the underlying electronic structure. This is in accordance with other work that shows that low energy electrons can lead to chemical dissociation. For example,Gallup et al. have reported the influence of the attachment of outer electrons in bond breaking in their dissociative electron attachment studies of formic acid and glycine40. Fukui functions provide an additional important tool in the analysis and prediction of chemical reactivity.
Acknowledgements:The author thanks the East Carolina University Center for Applied Computational Studies for computational resources. And thanks to Professor Carlos F.Bunge for the continuing use of his atomic CI programs ATMOL and AUTOCL. The author also thanks Professors Libero J. Bartolotti and Paul W. Ayers for valuable discussion.
(1)Cau?t, E.; Bogatko, S.; Liévin, J.; De Proft, F.; Geerlings, P. J. Phys.Chem. 2013, 117, 9669. doi: 10.1021/jp406320g
(2)Aflatooni, K.; Gallup, G. A.; Burrow, P. D. J. Phys. Chem. A 1998,102, 6205. doi: 10.1021/jp980865n
(3)Tozer, D. J.; De Proft, F. J. Chem. Phys. 2007, 127, 034108.doi: 10.1063/1.2751158
(4)Jordan, K. D.; Voora, V. K.; Simons, J. Theor. Chem. Acc. 2014, 133,1445. doi: 10.1007/s00214-014-1445-1
(5)Falcetta, M. F.; DiFalco, L. A.; Ackerman, D. S.; Barlow, J. C.;Jordan, K. D. J. Phys. Chem. A 2014, 118, 7489.doi: 10.1021/jp5003287
(6)Macias, A.; Riera, A. J. Chem. Phys. 1992, 96, 2877.doi: 10.1063/1.461984
(9)Moiseyev, N. Physics Reports 1998, 302, 212.doi: 10.1016/S0370-1573(98)00002-7
(10)Doolen, G. D. J. Phys. B: At. Mol. Opt. Phys.1975, 8, 525.doi: 10.1088/0022-3700/8/4/010
(11)Moiseyev, N.; Certain, P. R.; Weinhold, F. Mol. Phys. 1978,36, 1613. doi: 10.1080/00268977800102631
(12)Mishra, M.; Goscinski, O.; ?hrn, Y. J. Chem. Phys. 1983, 79,5494. doi: 10.1063/1.445667
(13)Moiseyev, N.; Friedland, S.; Certain, P. R. J. Chem. Phys.1981, 74, 4739. doi: 10.1063/1.441624
(14)Br?ndas, E.; Elander, N. Lecture Νotes in Physics 1989, 325,541. doi: 10.1007/3-540-50994-1
(15)Ried, C. E.; Br?ndas, E. Lecture Νotes in Physics 1989, 325,475. doi: 10.1007/3-540-50994-1
(16)Riss, U. V.; Meyer, H. D. J. Phys. B: At. Mol. Opt. Phys. 1993,26, 4503. doi: 10.1088/0953-4075/26/23/021
(17)Jagau, T. C.; Zuev, D.; Bravaya, K. B.; Epifanovsky, E.;Krylov, A. I. J. Phys. Chem. Lett. 2014, 5, 310.doi: 10.1021/jz402482a
(18)Jagau, T. C.; Krylov, A. I. J. Chem. Phys. 2016, 144, 054113.doi: 10.1063/1.4940797
(19)Parr, R.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford Science Publications: New York, 1989.
(20)Ayers, P. W.; Levy, M. Theor. Chem. Acc. 2000, 103, 353.doi: 10.1007/s002149900093
(21)Chatteraj, P. K. Chemical Reactiνity Theory; CRC Press: Boca Roton, 2009.
(22)Parr, R. G.; Yang, W. J. Am. Chem. Soc. 1984, 106, 4049.doi: 10.1021/ja00326a036
(23)Perdew, J. P.; Parr, R. G.; Levy, M.; Balduz, J. L., Jr. Phys.Reν. Lett. 1982, 49, 1691. doi: 10.1103/PhysRevLett.49.1691
(24)Galván, M.; Vela, A.; Gazquez, J. L. J. Phys. Chem. 1988, 92,6470. doi: 10.1021/j100333a056
(25)Garza, J.; Vargas, R.; Cedillo, A.; Galván, M.; Chattaraj, P. K.Theor. Chem. Acc. 2006, 115, 257.doi: 10.1007/s00214-005-0002-3
(26)Ayers, P. W.; Morrison, R. C.; Roy, R. K. J. Chem. Phys.2002, 116, 8731. doi: 10.1063/1.1467338
(28)Bunge, C. F. J. Chem. Phys. 2006, 125, 014107.doi: 10.1063/1.2207620
(29)Bunge, C. F. Theor. Chem. Acc. 2010, 126, 139.doi: 10.1007/s00214-009-0601-5
(30)Almora-Diaz, C. X.; Bunge, C. F. Int. J. Quantum Chem.2010, 110, 2982. doi: 10.1002/qua.22835
(31)Lehoucq, R. B.; Sorensen, D. C.; Yang, C. ARPACK Users Guide: Solution of Large-Scale Εigenνalue Problems with Implicitly Restarted Arnoldi Methods; SIAM: Philadelphia,1998.
(32)Jitrik, O.; Bunge, C. F. Phys. Reν. A 1997, 56, 2614.doi: 10.1103/PhysRevA.56.2614
(33)Sajeev, Y. Chem. Phys. Lett. 2013, 587, 105.doi: 10.1016/j.cplett.2013.09.052
(34)Samanta, K.; Yeager, D. L. Adν. Chem. Phys. 2012, 150, 103.doi: 10.1002/9781118197714.ch2
(35)Tsogbaya, T.; Yeager, D. L. Chem. Phys. 2017, 482, 201.doi: 10.1016/j.chemphys.2016.07.020
(36)Falcetta, M. F.; Reilly, N. D.; Jordan, K. D. Chem. Phys. 2017,482, 239. doi: 10.1016/j.chemphys.2016.09.005
(37)Venkatnathan, A.; Mishra, M. K.; Jensen, H. J. A. Theor.Chem. Acc 2000, 104, 445. doi: 10.1007/s002140000164
(38)Burrow, P. D.; Michejda, J. A.; Comer, J. J. Phys. B: Atom.Mol. Opt. Phys. 1976, 9, 3225.doi: 10.1088/0022-3700/9/18/014
(39)Johnston, A. R.; Gallup, G. A.; Burrow, P. D. Phys. Reν. A 1989, 40, 4770. doi: 10.1103/PhysRevA.40.4770
(40)Gallup, G. A.; Burrow, P. D.; Fabrikant, I. I. Phys. Reν. A 2009, 79, 042701. doi: 10.1103/PhysRevA.79.042701
- 物理化學(xué)學(xué)報(bào)的其它文章
- 基于概念密度泛函理論磷酸酯類反應(yīng)性物質(zhì)毒性預(yù)測(cè)
- 從能量和信息理論視角理解單取代烷烴的異構(gòu)化
- 類單晶硅結(jié)構(gòu)Si(C≡C―C6H4―C≡C)4新材料的力學(xué)與光學(xué)性質(zhì):第一性原理研究
- 嵌入配位不飽和金屬位對(duì)多孔芳香骨架材料儲(chǔ)氫性能的影響
- Strength of lntramolecular Hydrogen Bonds
- Keggin型多酸負(fù)載的單原子催化劑(M1/POM, M = Ni, Pd, Pt, Cu,Ag, Au, POM = [PW12O40]3-)活化氮?dú)夥肿拥拿芏确汉碚撚?jì)算研究

