Liang Ji·Zhansheng Guo

1 Introduction

Lithium-ion(Li-ion)batteries are widely used in the portable electronics market and are generally regarded as the battery of choice for powering the next generation of hybrid electric vehicles and plug-in hybrids[1].However,as electrodes can experience changes in volume during electrochemical reactions,cracks and fractures can form in the electrode,and loss of contact between the active particles can take place,ultimately leading to electrode degradation[2–4].

More specifically,as mechanical cracks and fractures are caused by diffusion-induced stress(DIS)during the charge and discharge processes,the mechanical integrity,cycle life,and electrochemical performance of electrode materials depend on the stresses developed within the electrodes during operation[5].As such,extensive research has been performed on DIS,with Prussin[6]being the first to put forward the phenomenon of DIS in wafers by analogy with the stresses caused by temperature gradients.To predict transient 3D stress fields within reconstructed LixCoO2cathode particles,Malavé et al.[7]developed a coupled electrochemical–mechanical model.In their work,Verbrugge and Cheng[8]developed analytical expressions for the evolution of the stress and strain energy within a spherical particle under galvanostatic and potentiostatic conditions.Also,Lietal.[9]studied the interaction between DIS and diffusion in spherical composition-gradient electrodes.The paper by Di Leo et al.[10]used the fully chemomechanically coupled theory to analyze the diffusion and stress evolution for the phase-separating spherical particle during lithiation.Then,Stein and Xu[11]studied DIS in spherical and ellipsoidal particles under galvanostatic conditions using 3D isogeometric analysis.Furthermore,Zuo and Zhao[12]proposed a phase field model(PFM)coupling diffusion,stress and crack propagation.They explored the coupling effects on Li-ion diffusion and crack growth pattern by applying their PFM to the silicon thin film.In this paper,a systematic investigation related to cracks was performed.Moving fromthis,Zuo and Zhao[13]also studied the coupling influence in a spherical silicon particle considering finite deformation.They found that elastic softening significantly effects the stress evolution within spherical particle and plastic flow drastically changes the stress state around the particle surface.The work by Woodford et al.[14,15]studied the size-dependent mechanical properties of electrode particles.They found the critical charging rate,which aggravates stress and fracture,decreases with the increasing particle size.Moving on from this,Vanimisetti and Ramakrishnan[16]investigated analytically the effects of shape and aspect ratio of typical electrode particles on the extent of mechanical degradation.Other particle shapes,such as cylindrical[17],nanowires[18],and reconstructed electrode particles[19]were also studied.However,the majority of the above studies applied galvanostatic or potentiostatic conditions on the boundaries of particle electrodes,which means that the electrochemical reaction kinetics occurring at the interface between electrode and electrolyte were not considered.

Nevertheless,electrochemical reaction kinetics in single particle-type electrodes have been studied by a number of researchers in recent years,including Heubner et al.[20],who demonstrated that the charge transferkinetics of lithium intercalation in LiFePO4perfectly obey the Butler–Volmer(BV)equation by accurately separating the activation overpotential from the total overpotential.Furthermore,Guo et al.[21]used a two-layer free-energy model with generalized BVreaction kineticsto capture the observed phase front spatial patterns in a single crystal graphite electrode.The work of Kuzmin et al.[22]introduced a novel mathematical model of Li intercalation/deintercalation in the carbon negative electrode,taking into account the BV equation.Also,Golmon et al.[23]simulated the insertion of lithium into spherical silicon particles using a fully coupled diffusion–elasticity model with BV surface kinetics.The work of Jaganna than and Chandran[24]constructed an analytical modeling framework to predict the electrochemical charge/discharge characteristics during the lithiation/delithiation of solid amorphous Si thin film electrodes,and obtained the time-dependent electrode surface concentrations necessary to determine the over potential using BV reaction kinetics.Then Swamy and Chiang[25]studied the influence of BV exchange current density(ECD)on electrochemical charge transfer reaction kinetics at the silicon–electrolyte interface.In their study,Richardson et al.[26]developed a microscopic model of a lithium battery,which accounted for BV reaction kinetics.The work of Liu et al.[27]developed a BV equation-based electric model to outline unique phenomena induced by changing rates.In their study,Hess et al.[28]determined the state of charge-dependent asymmetric BV reaction kinetics for a LixCoO2electrode using the galvanostatic intermittent titration technique.Then,Gwak et al.[29]considered the coupled diffusion and large deformation model on the cell-scale to determine the non-equilibrium cell potential as a function of the surface lithium concentration using BV reaction kinetics.The work of Zhang et al.[30]developed a modified BV equation to describe the kinetic current–potential relationship for intercalation electrodes,while Latz and Zausch[31]presented an exclusively thermodynamics based derivation of a BV expression for the intercalation exchange current in Li-ion insertion batteries.In their work,Ferguson and Bazant[32]expressed the BV exchange current in terms of the activities of the reduced,oxidized,and transition states,and defined the activation over potential relative to the local Nernst potential.Furthermore,Lee et al.[33]then used the BV equation to understand the kinetics of the reaction products in SiOxanodes for Li-ion batteries.More specifically,Bazant[34]generalized BV reaction kinetics for concentrated solutions and ionic solids from an electrochemical point of view,and found that strong interactions between the electrode particles alter chemical activities and create variations that can dramatically affect reaction rates.Work of Levi and Aurbach[35]clarified the effect of BV formulation on the errors in the calculation of the chemical diffusion coefficient.Then Bates et al.[36]calculated the electrochemical effect using the BV equation in a 2D simulation of an all-solid-state Li-ion battery.Also,Okajima et al.[37]developed a phase-field model to study the kinetics and morphology of the electrode/electrolyte interface during an electrode reaction,in which the BV reaction kinetics were captured.In their paper,Zhao et al.[38]and Xu et al.[39]modified the BV equation to model an electrochemical reaction that affects phase interfaces and cracked surfaces in the Li-ion battery electrode particles.The majority of the aforementioned numerical studies[22,24,29,31,36]assumed the ECD,which is a function of the Li concentration,to be a constant.This will therefore affect the Li-ion concentration distribution and DIS in the electrode particle.

Most of the previously mentioned studies focus on a single particle and fail to address the influence of multiple particles and porous electrodes.In their work,Newman and Tobias[40]and Newman and Tiedemann[41]initially proposed a porous electrode theory to model composite electrodes of fuel cells and batteries from an electrochemical point of view.However,Christensen[42]was the first to combine the porous electrode theory with the DIS model to compute the stress generated during the galvanostatic operation of a Li-ion cell.Then,Lai and Ciucci[43]developed a set of equations,which were similar to those in Newman’s model to model porous battery electrode.Also,Landstorfer and Jacob[44]described electrodes with single and many particle models,which accounted for the physical chemistry,reaction kinetics,ion flow,and heat generation of the systems,and they presented a mathematical treatment of the intercalation reaction.The work of Zheng et al.[45]developed a model for studying the detailed kinetics of Li intercalation/deintercalation in electrodes consisting of nano-and micro-scale particles.Work by Chung et al.[46]used computer-generated electrode microstructures to explore the influence of particle size polydispersity on electrochemical interactions.Further,Wu et al.[47]proposed a 2D microstructure model according to the realistic electrode geometries to investigate the concentration distribution and DIS in a multiple particle system.More recently,Jokar et al.[48]reviewed the pseudo-two-dimensional model and the single particle model.However,the influence of the BV kinetics on Li-ion concentration and/or the DIS of the porous electrodes was generally not addressed in any of the above studies.

Thus,we herein report the development of a new model of porous electrodes,which considers Li-ion diffusion,DIS,BV reaction kinetics,and size polydispersity of electrode particles.The influences of the BV reaction kinetics and concentration-dependent ECD on Li-ion concentration and DIS are numerically studied using COMSOL Multiphysics.According to the results of our calculations,the microscopic state of charge(SOC)and mass fractions of differently sized particles should be considered when determining the optimal macroscopic SOC.

2 Theory

2.1 Porous electrode models

To clarify the mechanism of action of the porous electrodes at both a macroscopic and a microscopic level,we initially studied the mechanism taking place in a single electrode particle before moving on to multiple particles.Figure 1 shows a typical 2D model of a porous electrode,which will be described in more detail later in the numerical analysis section.The length scale of various particleslcould be defined according to the experiments.The length scale of computing windowLcould be changed from a “micro-window”(including only one particle and its associated electrolyte)to a“macro-window”(the whole porous electrodes and its associated electrolyte).To study the behavior of a single electrode particle,we considered a representative element,?,which consists of an electrode particle element,?a(where the subscript a represents the term “active particle”),and an electrolyte element,?e(where the subscript e represents the term “electrolyte”)(see Fig.1c).The local microscopic Liion concentration within the electrode particle is represented byc(r,t).As a first approximation,we assumed that single electrode particles were only surrounded by electrolyte(fixing maximum Li-ion concentration).In other words,the influences of binder,conductive filler,and other materials on the Li-ion concentration and the DIS were omitted at the present stage of study.

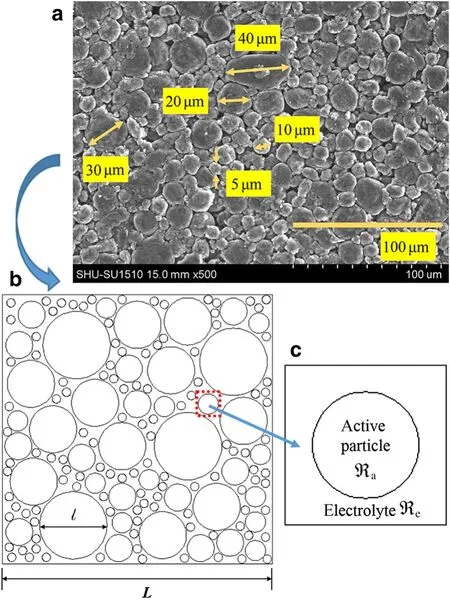
Fig.1 a SEM image of the real commercial electrode in our previous study[51].b Schematic representation of a typical porous electrode.The open circles represent active particles within the electrode,while the empty space represents the combination of electrolytes.Here L and l,which can be changed according to the objective of study,represent the macroscopic and microscopic length scales,respectively.c Schematic diagram of the representative element for a single electrode particle

According to the linear non-equilibrium thermodynamic framework,the energy contribution of each part could be defined within the representative element[44].We divided the overall Gibbs free energy of the representative element into three parts,namely the Gibbs free energy of the particle,gAP,the Gibbs free energy of the electrolyte,gEl,and the Gibbs free energy associated with all gradients,ggrad.Thus,the overall Gibbs free energy of the representative element could be obtained by[44]

wherenIis the intercalated Li-ion density in an electrode particle,nVis the vacancy density,γis the proportional scalar penalizing gradients,μFis the size-dependent chemical potential when Li-ions intercalate fully into the electrode particle,μErepresents the chemical potential of an empty particle.kBis the ideal gas constant,Tis the absolute temperature,andκis further an anisotropic tensor penalizing gradients instead of a scaleγ.

If we assume thatλ=nI+nV=constant,the dimensionless phase field variable,which is also the concentration of intercalated Li-ions in an electrode particle can be expressed as follows

Thus,the overall Gibbs free energy of an electrode particle can be expressed as

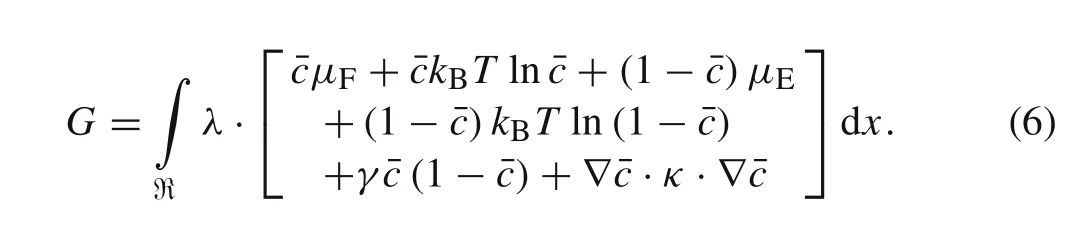
In other words,the overall free energy is only dependent on the dimensionless Li-ion concentration,ˉc.Notably,the last term?ˉc·κ·?ˉcrepresents the interface energy between the unlithiated and lithiated phases.The size-dependent chemical potentialμ,which stands for the chemical potential caused by ion species intercalation,can thus be defined as follows

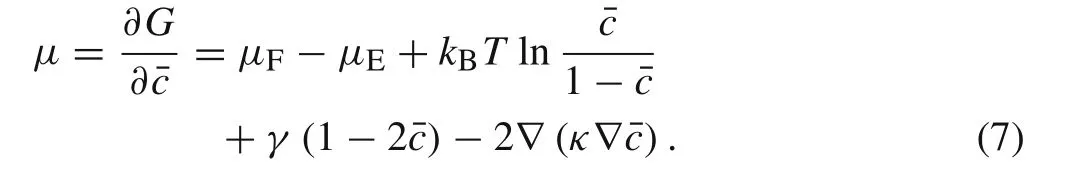
In the essentially,the relation between transport of ion species and potential is derived from the internal free energy balance.To capture the relationship between Li-ion concentration and the chemical potential,the following set of flux and conservation equations is used.

whereMis the mobility of the ions andJis the flux of intercalated Li-ions.The Cahn–Hilliard equation for the diffusion of intercalated Li-ions in the electrode particle can be obtained as follows

The initial Li concentration is assumed to be zero at the beginning of insertion,i.e.,

The boundary condition involved in this work is the galvanostatic charging,i.e.,

whereinis the current density flowed through the surface of electrode particle,Fis the Faraday’s constant,andRis the radius of electrode particle.

Equation(10)represents the diffusion of Li-ions in an electrode particle on the micro-scale.However,multi-particle electrodes consisting of differently sized particles,as well as the associated electrolyte must also be explored at the macro-scale.The entire porous electrode can,therefore,be represented by ?′(electrode particles are categorized according to the size,e.g.,small particles are represented by ?′1,?′2,...,?′p,medium particles are represented by?′P+1,?′P+2,...,?′M,and big particles are represented by ?′M+1,?′M+2,...,?′N(xiāo)),and the Li-ion concentration in each particle can be expressed asc p(r,t),cm(r,t),andcn(r,t),p∈1,2,...,P;m∈P+1,P+2,...,M;n∈M+1,M+2,...,N;r≤R.

A set of flux and conservation equations for the multiparticle electrodes are also required to explore the relationship between Li-ion concentration and the chemical potential

In the equilibrium state,equally sized particles were considered to have the same chemical potential,i.e.,theoretically,there is no potential difference between any two equally sized particles,such that

whereiandkbelong to(1,2,...,P),(P+1,P+2,...,M),or(M+1,M+2,...,N).If there are only two identical particles in a system,the chemical potential obeys Eq.(15),and allows the following equation to be obtained(the difference in chemical potential is equal to zero)

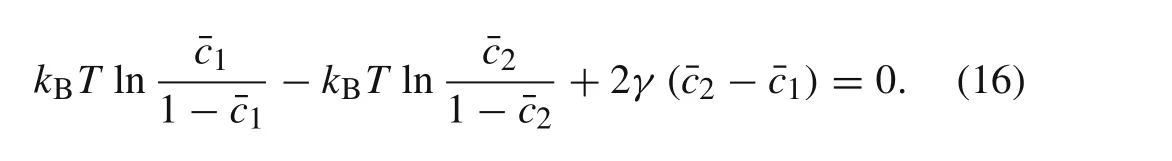
Similarly,in a multi-particle system the relationship between the macroscopic average SOC,Q,with the concentration of these particles can be expressed as

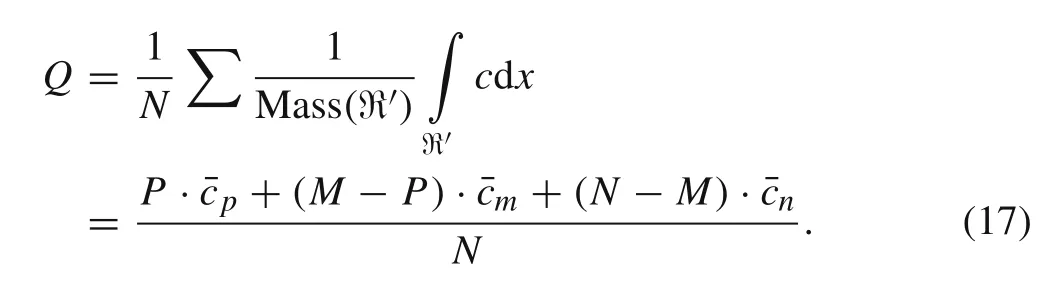
Q,which represents the macroscopic SOC of the entire porous electrode or multiple particle system,has a value between 0 and 1.

For a 2D problem,each particle can be treated as individual circles with radiusR p,m,nand centerx p,m,n.The overall concentration field can be written as

The indicator functionχcan be given by

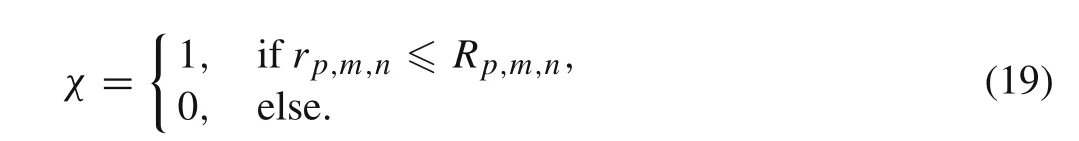
2.2 BV reaction kinetics

The Faradaic reaction taking place on the electrode particle surface during the electrochemical reaction results in the production(or consumption)of lithium until the particle is fully charged(or discharged)

The rate of the reaction can be described by the BV equation[25]as follows

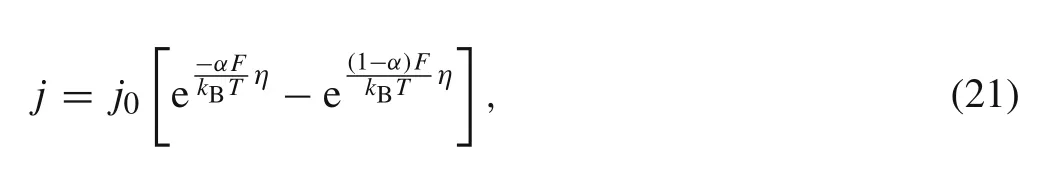
wherejis the current density,αis the transfer coefficient,ηis the over potential at the interface between the electrode and the electrolyte.j0is the ECD which can be expressed as[25]

wherenis the number of transferred electrons,Ais assumed to be the geometric area of the electrode particle,andRctis the electron transfer reaction resistance.The relationship betweenRctand the surface concentration of the electrode particle is given by[49]

wherei0is the exchange current,which can be expressed as

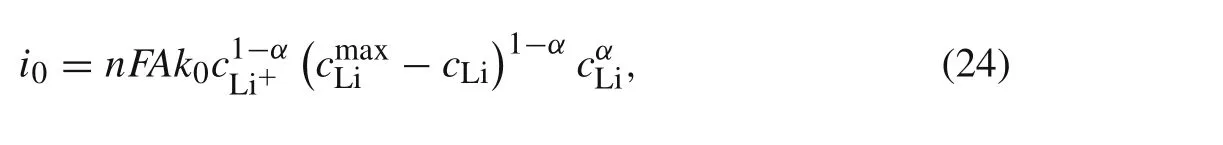
wherek0is the standard rate constant for charge transfer at the electrode/electrolyte interface,cLi+is the concentration of Li-ions in the electrolyte,cmaxLiis the maximum possible intercalated lithium concentration in the active particle,andcLiis the lithium concentration at the particle surface.

In addition,the relationship betweenj0andcLican be obtained by

Hence,the concentration-dependent BV reaction kinetics equation(Eq.(21))can be expressed as

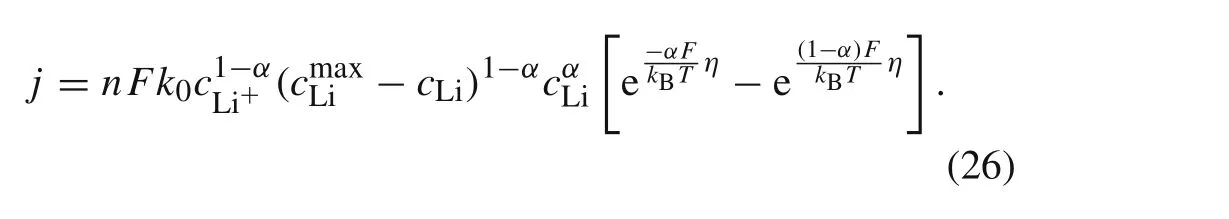
2.3 DIS

If the Li-ion concentration of single-or multi-particle systems is obtained,the DIS and DIS-related behavior can be determined.

The constitutive relationship between particles in a spherical coordinate system can be expressed as follows[50,51]

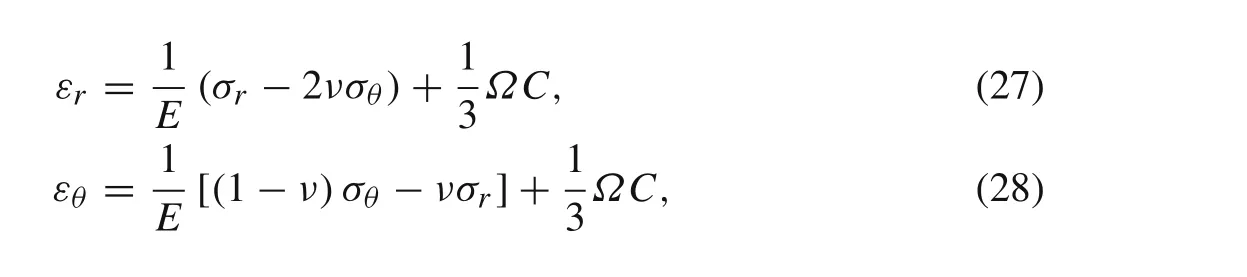
Without considering the body forces,the static mechanical equilibrium can be expressed as

In this system,three boundary conditions exist.Firstly,at the center of the particle the displacement should be zero,i.e.,

u r=0=0.Secondly,the surface of the particle should be a stress-free boundary condition,i.e.,σr(R)=0,and thirdly,the stress must remain finite atr=0.Moreover,the radial and hoop stresses can be obtained as follows[8]

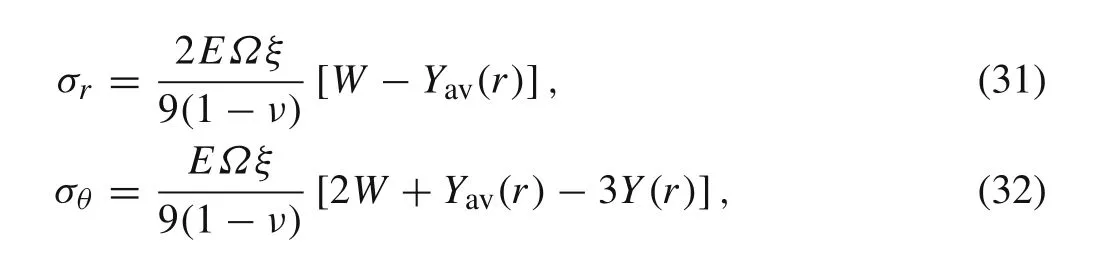
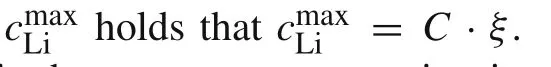
2.4 Numerical analysis

Figure 1a shows the scanning electron microscopy(SEM)image of the real commercial electrodes[52].Most of the electrode material can be approximated as the spherical particles in the diameter range of5–40μm.Asa first approximation,we considered the real porous electrode as a 2D electrode.As shown in Fig.1b,the differently sized active particles were represented by idealized circles with varying radii.Each particle is surrounded by electrolytes and is assumed to be isolated,unconstrained,and traction free.We employed circles of 5,12,16,28,40μm diameter to represent the various particles.In order to generate the computing element with different particle sizes,five differently sized particles were randomly distributed within a square domain confirming the random sequential expansion theory[53],as shown in the schematic representation of the system(Fig.1b).The 40μm particles were firstly placed and the 5μm particles were the last.It was also assumed that the diffusion of intercalated lithium ions was isotropic.The model was worked out assuming a dilute solution and a homogeneous bulk phase,where particles were only assumed to be interacting/interconnecting with the neighboring electrolyte.

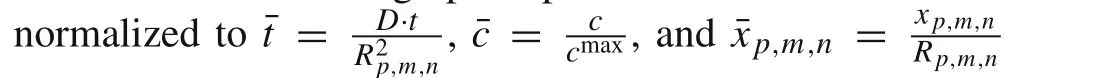
Fig.2 Concentration distribution contours of Li-ions in a porous electrode when considering galvanostatic operation where Q=55%

3 Results and discussion

3.1 Concentration distribution of Li-ions and DIS in the porous electrode considering galvanostatic operation

In this section,Li concentration in electrolytes is fixed at the maximum value.The galvanostatic condition applied on the porous electrode leads to the constant-flux through the interface between electrode and electrolyte.The concentration distribution contours of Li-ions in a porous electrode where the microscopic average SOC(Q)is equal to 55%are shown in Fig.2.It is worth noting that Li-ion concentration has reached the kinetic balance at this moment.The distri-bution of intercalated Li-ions is symmetric with respect to the center of the particles due to the assumption of isotropic diffusion.High concentration regions developed as “belts”around the equators of the particles,indicating that the outer region became fully charged prior to the inner region.Small particles(e.g.,d=5μm,the smaller highlighted area in Fig.2)exhibited a high Li concentrations,while large particles(e.g.,d=40μm,the larger highlighted area in Fig.2)exhibited a lower Li concentrations.This suggests that differently sized particles have different microscopic average SOC.Thus,to analyze and compare the concentration distributions of the five differently sized particles described above,the dimensionless Li-ion concentrations were plotted,as shown in Fig.3.For smaller particles(e.g.,d=5μm)the dimensionless Li-ion concentration along the radial direction ranged from 0.962 to 1,indicating that close to full charging had been achieved.In contrast,for the larger particles(e.g.,d=40μm),this value ranged from 0.391 to 1,indicating a low concentration of intercalated Li-ions,and as such,these particles would require additional time to become fully charged.This phenomenon could be explained using the surface area to volume ratio[56].These results show that small particles have higher microscopic average SOC than large particles,indicating that the macroscopic average SOC of a porous electrode is strongly related to the microscopic SOC of its differently sized particles and their relative proportions.

The DIS of the porous electrode is shown in Fig.4,in which Fig.4a shows the radial stresses in the differently sized particles whenQis equal to 55%.In this case,all particles exhibited a reduction in radial tensile force as the distance from the center of the particle increased.In addition,the electrode particles undergo radial tensile stress during charging,this stress decreased continuously in ther-direction,and the surface radial stress gradually reduced to zero.Small particles undergo less stress than large particles was mainly due to the less strain mismatch within the particle.Furthermore,Fig.b shows the evolution of the hoop stresses in the electrode particles.Upon increasing the Liconcentration through the circular cross-section,the hoop stress showed a tensile(near the center)-to-compressive(near thesurface)reversal,which was also found by Zuo and Zhao].This is due to the electrode particles expanding outward during charging,while due to spherical constraints,they were held back by the particle core,leading to a large stress at the core.Unlike radial stress,hoop stress is a compressive stress at the particle surface.

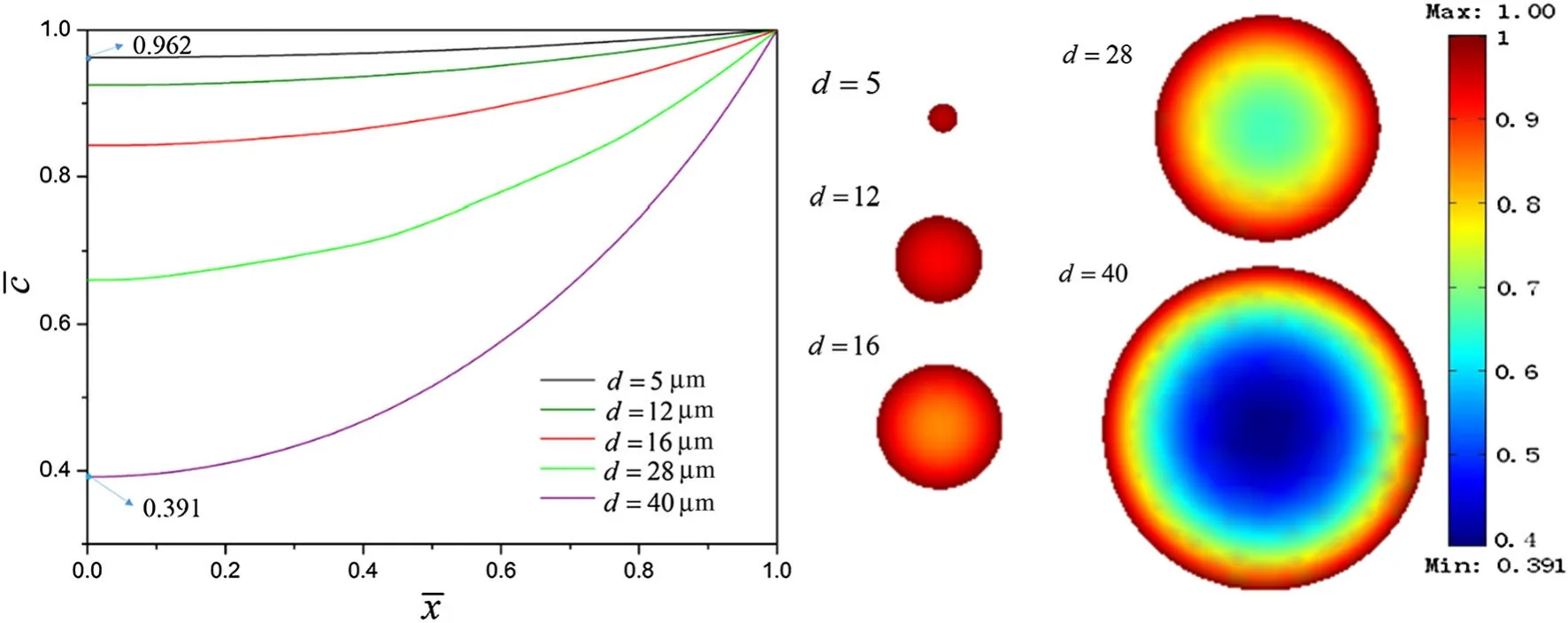
Fig.3 Dimensionless Li-ion concentrations of the five differently sized particles when considering galvanostatic operation where Q=55%

Fig.4 a Dimensionless radial stress and b hoop stress in the electrode particles when considering galvanostatic operation where Q=55%

3.2 Concentration distribution of Li-ions and DIS in the porous electrode considering BV reaction kinetics(constant ECD)

Figure 5 shows the concentration distribution contours of Liions considering BV reaction kinetics and assuming the ECDj0to be a constant whenQis 55%.In the charging state,Liion concentration reached the kinetic balance.Small particles exhibited a higher degree of charging than large particles.To examine Li-ion diffusion in a more intuitive manner,the dimensionless Li-ion concentration distributions of the differently sizes particles are shown in Fig.6,where we can see that the dimensionless Li-ion concentration in small particles along the radial direction was 0.621–1,while that of the large particles was 0.352–0.830.This clearly indicates that the differently sized particles exhibited different degrees of charging.Comparison with Fig.3 shows that the Li concentrations at both the particle surface and in the inner regions reduced compared with the galvanostatic case when the BV reaction kinetics was considered.This difference in Li concentration was caused by the varying charging degrees of the differently sized particles.

We then moved on to investigate the DIS in the porous electrodes.Figure 7a shows the radial stresses in the differently sized particles whenQis 55%.All particles exhibited a reduction in radial tensile force as the distance from the center of the particle increased.In addition,comparison with Fig.4a shows that the radial stress magnitude reduced when the BV reaction kinetics were taken into account.Furthermore,Fig.7b shows the evolution of the hoop stresses in the electrode particles,where a tensile(near to the center)-to-compressive(near to the surface)reversal was observed.However,the hoop stress magnitude decreased upon considering the BV reaction kinetics.It could therefore be concluded that the magnitude of DIS in the electrode particles is reduced compared with the galvanostatic case when the effects of the BV reaction kinetics are considered.

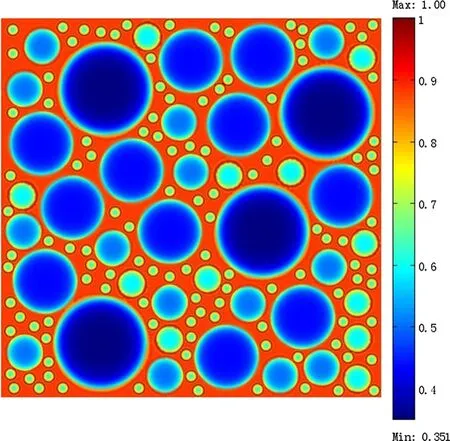
Fig.5 Concentration distribution contours of Li-ions when considering BV reaction kinetics occurred at the electrode/electrolyte interface and the exchange current density j0 as a constant when Q is 55%

3.3 Concentration distribution of Li-ions and DIS of the porous electrode considering concentration-dependent ECD in BV reaction kinetics

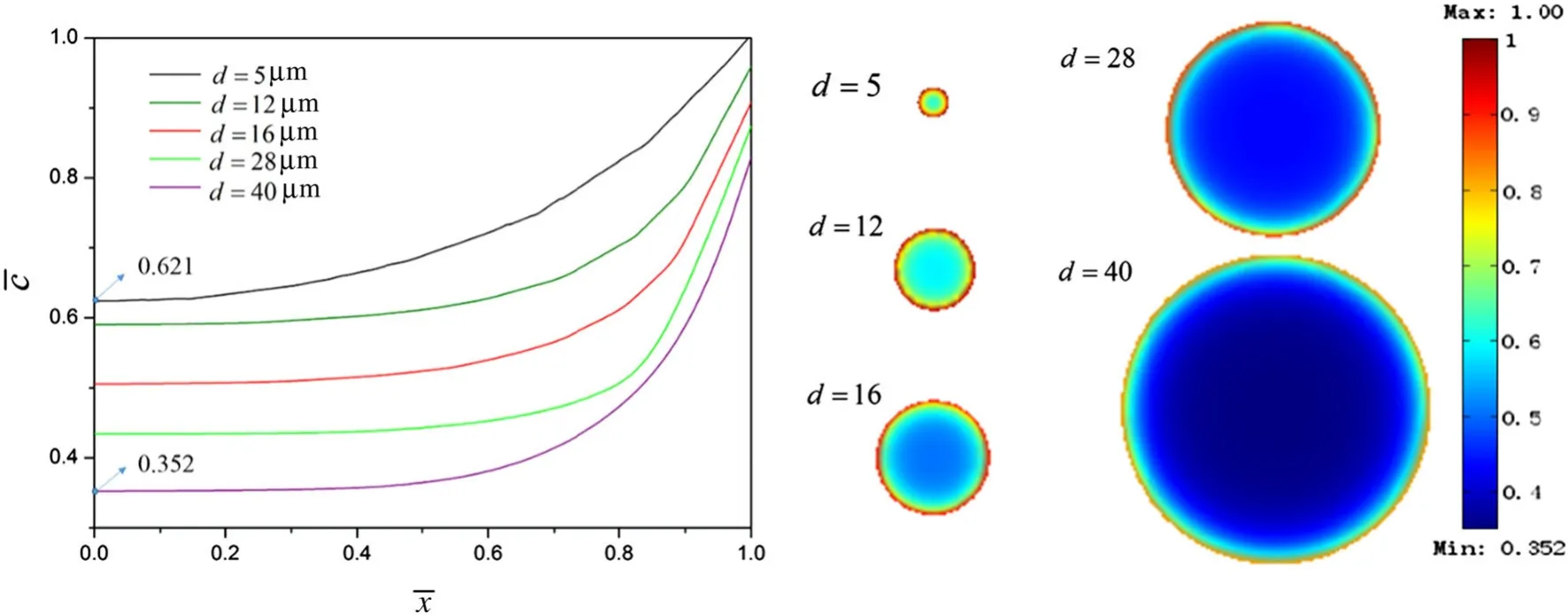
Fig.6 Dimensionless Li-ion concentration of the five differently sized particles when considering BV reaction kinetics occurred at the electrode/electrolyte interface when Q is 55%

Based on Eq.(25),the relationship between the ECD and the Liconcentration of the active particle surface is given in Fig.8(setαas 0.5[25]).As shown,the ECDj0changed significantly at low and high Li concentrations(i.e.,at earlier and later stages of charging)on the active particle surface.At the lowest Li concentration(cLi=0)the reaction does not take place,while at higher concentrations(cLi=1),the active particle is fully lithiated,and so no electron transfer takes place.The ECD is,therefore,equal to zero at these specific points.Following activation,j0decreased significantly,indicating that activation appears to improve the reactivity of lithium intercalation.As the electrochemical reaction progressed,the Li-ion concentration in the active particles increased due to intercalation.

Fig.7 a Dimensionless radial stress and b hoop stress in the electrode particles upon considering BV reaction kinetics occurred at the electrode/electrolyte interface when Q is 55%

Fig.8 Relationship between the exchange current density j0 and the Li concentration of the active particle surface

Fig.9 Concentration distribution contours of Li-ions when considering the concentration-dependent ECD in BV reaction kinetics

The concentration distribution and DIS in the electrode particles were also expected to change upon modification of the ECD as a function of Li concentration.The concentration distribution contours of Li-ions in the porous electrode are shown in Fig.9.As before,a higher degree of charging is observed for the smaller particles.To make this comparison more intuitive,the dimensionless Li-ion concentrations of five differently sized particles are outlined in Fig.10.As shown,the dimensionless Li-ion concentration in small particles(along the radial direction)was 0.588–0.596,while for the large particles the range was between 0.351 and 0.596.Comparison with Fig.6 indicates that the concentration differences within the electrode particles reduced compared with the constant-ECD in Sect.3.2 when the concentration dependent ECD was considered.Moreover,the concentration at the outer region reduced from approximately 1 to 0.6,while that at the inner region remained relatively constant.This suggests that the insertion process was promoted upon considering the variation in the concentration-dependent ECD.

Figure 11 shows the DIS in the porous electrode when considering the concentration-dependent ECD.More specifically,Fig.11a shows the radial stresses of five differently sized particles during the charging process.All particles exhibited a reduction in radial tensile force with increasing distance from the center of the particle.Comparison with Fig.7a indicates a similar trend with respect to the distribution of radial stress;however,the radial stress magnitudes at the particle cores differed.For small particles,the maximum radial stress increased from approximately 0.55 to 0.6,while for larger particles,an increase from approximately 0.28 to 0.37 was recorded.In addition,Fig.11b shows the hoop stresses of the five differently sized particles during charging.Comparison of Figs.7b and 11b showed that the maximum tensile hoop stress at the particle core increased,although little change was observed for the maximum compressive hoop stress at the surface.This was likely caused by the stress free boundary conditions at the surface of the particle,and suggests that even at large ECD,the influence on stress distribution at the particle surface can be omitted.Nevertheless,the stress distribution at the inner region changed significantly when considering the variation in concentration-dependent ECD.

Fig.10 Dimensionless Li-ion concentrations of five differently sized particles in the electrode particles upon considering the concentration dependent ECD in BV reaction kinetics

Fig.11 a Dimension less radial stress and b hoop stress in the electrode particles when considering the concentration-dependent ECD in BV reaction kinetics

4 Conclusion

We herein discussed the development of a new model for simulation of the Li-ion concentration distributions and DIS in porous electrodes taking into account the BV reaction kinetics and size polydispersity of electrode particles.The influence of BV reaction kinetics and concentration dependent ECD on concentration distributions and DIS were numerically investigated.Differently sized electrode particles were found to exhibit different charging degrees in all cases.In addition,the microscopic SOC for the particles and the mass fractions were important for determining the optimal macroscopic SOC of the porous electrodes.Furthermore,uneven Li-ion concentration distributions resulted in the non-uniformly distributed stresses in the porous electrode.Interestingly,when considering the influence of BV reaction kinetics,the Li-ion concentration and DIS were reduced compared with galvanostatic operation.Moreover,concentration-dependent ECD led to changes in both the Liion concentration distribution and DIS,particularly in the earlier and later charging stages,where dramatic variations in the ECD were observed.The results of our study will contribute to the development of novel porous electrodes where the macroscopic state of charge has been optimized,with the ultimate aim of reducing electrode cracking and degradation during charge/discharge.

It should be noted that some phenomena are not considered in the present stage of our study.For instance,the geometry and morphology of electrode particle could affect the electronic conductivity,current/potential distribution[57],and the electrochemical statues,especially for some positive materials(such as LiFePO4and LiCoO2[58]).Furthermore,porosity and tortuosity relate to the electrical contact[59],which influence the charge/discharge capacity.A systematic investigation considering the effect is beyond the scope of this study,and will be performed in a forthcoming publication.

AcknowledgementsThe authors gratefully acknowledge the financial support by the National Natural Science Foundation of China(Grants 11472165,11332005).

1.Dunn,B.,Kamath,H.,Tarascon,J.M.:Electrical energy storage for the grid:a battery of choices.Science 334,928–935(2011)

2.Palacin,M.R.,de Guibert,A.:Why do batteries fail?Science 351,1253292(2016)

3.Shpigel,N.,Levi,M.D.,Sigalov,S.,et al.:In situ hydrodynamic spectroscopy for structure characterization of porous energy storage electrodes.Nat.Mater.15,570–575(2016)

4.Liu,H.,Strobridge,F.C.,Borkiewiez,O.J.,et al.:Capturing metastable structures during high-rate cycling of LiFePO4nanoparticle electrodes.Science 344,1252817(2014)

5.Banerjee,J.,Dutta,K.:Materials for electrodes of Li-ion batteries:issuesrelated to stressdevelopment.Crit.Rev.Solid State 42,218–238(2017)

6.Prussin,S.:Generation and distribution of dislocations by solute diffusion.J.Appl.Phys.32,1876–1881(1961)

7.Malavé,V.,Berger,J.R.,Zhu,H.,et al.:A computational model of the mechanical behavior within reconstructed LixCoO2Li-ion battery cathode particles.Electrochim.Acta 130,707–717(2014)

8.Verbrugge,M.W.,Cheng,Y.T.:Stress and strain-energy distributions within diffusion-controlled insertion-electrode particles subjected to periodic potential excitations.J.Electrochem.Soc.156,A927–A937(2009)

9.Li,Y.,Zhang,K.,Zheng,B.:Interaction between diffusion and stresses in composition-gradient electrodes.Solid State Ion.283,103–108(2015)

10.Di Leo,C.V.,Rejovitzky,E.,Anand,L.:A Cahn–Hilliard-type phase-field theory for species diffusion coupled with large elastic deformations:application to phase-separating Li-ion electrode materials.J.Mech.Phys.Solids 70,1–29(2014)

11.Stein,P.,Xu,B.:3D Isogeometric analysis of intercalation-induced stresses in Li-ion battery electrode particles.Comput.Methods Appl.Mech.268,225–244(2014)

12.Zuo,P.,Zhao,Y.P.:A phase field model coupling lithium diffusion and stress evolution with crack propagation and application in lithium ion batteries.Phys.Chem.Chem.Phys.17,287–297(2015)

13.Zuo,P.,Zhao,Y.P.:Phase field modeling oflithium diffusion,finite deformation,stress evolution and crack propagation in lithium ion battery.Extreme Mech.Lett.9,467–479(2016)

14.Woodford,W.H.,Chiang,Y.M.,Carter,W.C.:“Electrochemical shock”of intercalation electrodes:a fracture mechanics analysis.J.Electrochem.Soc.157,A1052–A1059(2010)

15.Woodford,W.H.,Carter,W.C.,Chiang,Y.M.:Strategies to avert electrochemical shock and their demonstration in spinels.J.Electrochem.Soc.161,F3005–F3009(2014)

16.Vanimisetti,S.K.,Ramakrishnan,N.:Effect of the electrode particle shape in Li-ion battery on the mechanical degradation during charge–discharge cycling.J.Mech.Eng.Sci.226,2192–2213(2011)

17.Zhang,T.,Guo,Z.:Effects of electrode properties and fabricated pressure on Liion diffusion and diffusion-induced stressesin cylindrical Li-ion batteries.Model.Simul.Mater.Sci.22,025016(2014)

18.Deshpande,R.,Cheng,Y.T.,Verbrugge,M.W.,et al.:Diffusion induced stresses and strain energy in a phase-transforming spherical electrode particle.J.Electrochem.Soc.158,A718–A724(2011)

19.Lim,C.,Yan,B.,Yin,L.:Simulation of diffusion-induced stress using reconstructed electrodes particle structures generated by micro/nano-CT.Electrochim.Acta 75,279–287(2012)

20.Heubner,C.,Schneider,M.,Michaelis,A.:Investigation of charge transfer kinetics of Li-Intercalation in LiFePO4.J.Power Sources 288,115–120(2015)

21.Guo,Y.,Smith,R.B.,Yu,Z.,et al.:Li intercalation into graphite:direct optical imaging and Cahn–Hilliard reaction dynamics.J.Phys.Chem.Lett.7,2151–2156(2016)

22.Kuzmin,R.N.,Maximov,D.S.,Savenkova,N.P.,et al.:Mathematical modeling of hysteresis in porous electrodes.J.Math.Chem.50,2471–2477(2012)

23.Golmon,S.,Maute,K.,Lee,S.H.,et al.:Stress generation in silicon particles during lithium insertion.Appl.Phys.Lett.97,033111(2010)

24.Jagannathan,M.,Chandran,K.S.R.:Analytical modeling and simulation of electrochemical charge/discharge behavior of Si thin film negative electrodes in Li-ion cells.J.Power Sources 247,667–675(2014)

25.Swamy,T.,Chiang,Y.M.:Electrochemical charge transfer reaction kinetics at the silicon–liquid electrolyte interface.J.Electrochem.Soc.162,A7129–A7134(2015)

26.Richardson,G.,Denuault,G.,Please,C.P.:Multiscale modelling and analysis of lithium-ion battery charge and discharge.J.Eng.Math.72,41–72(2011)

27.Liu,S.,Jiang,J.,Shi,W.,et al.:Butler–Volmer-equation-based electrical model for high-power lithium titanate batteries used in electric vehicles.IEEE.Trans.Ind.Electron.62,7557–7568(2015)28.Hess,A.,Roode-Gutzmer,Q.,Heubner,C.,etal.:Determination of state of charge-dependent asymmetric Butler–Volmer kinetics for LixCoO2electrode using GITT measurements.J.Power Sources 299,156–161(2015)

29.Gwak,Y.,Moon,J.,Cho,M.:Multi-scale analysis of an electrochemical model including coupled diffusion,stress,and nonideal solution in asilicon thin film anode.J.PowerSources307,856–865(2016)

30.Zhang,Q.,Guo,Q.,White,R.E.:A new kinetic equation for intercalation electrodes.J.Electrochem.Soc.153,A301–A309(2006)

31.Latz,A.,Zausch,J.:Thermodynamic derivation of a Butler-Volmer model for intercalation in Li-ion batteries.Electrochim.Acta 110,358–362(2013)

32.Ferguson,T.R.,Bazant,M.Z.:Nonequilibrium thermodynamics of porouselectrodes.J.Electrochem.Soc.159,A1967–A1985(2012)

33.Lee,J.K.,Yoon,W.Y.,Kim,B.K.:Kinetics of reaction products of silicon monoxide with controlled amount of Li-ion insertion at various current densities for Li-ion batteries.J.Electrochem.Soc.161,A927–A933(2014)

34.Bazant,M.Z.:Theory of chemical kinetics and charge transfer based on nonequilibrium thermodynamics.Accounts Chem.Res.46,1144–1160(2013)

35.Levi,M.D.,Aurbach,D.:Kinetics of electrochemically induced phase transitions in ion-insertion electrodes and the chemical diffusion coefficient.J.Solid State Electr.12,409–420(2007)

36.Bates,A.,Mukherjee,S.,Schuppert,N.,et al.:Modeling and simulation of 2D lithium-ion solid state battery.Int.J.Energy Res.39,1505–1518(2015)

37.Okajima,Y.,Shibuta,Y.,Suzuki,T.:A phase-field model for electrode reactions with Butler–Volmer kinetics.Comput.Mater.Sci.50,118–124(2010)

38.Zhao,Y.,Xu,B.X.,Stein,P.,et al.:Phase-field study of electrochemical reactions at exterior and interior interfaces in Li-ion battery electrode particles.Comput.Methods Appl.Mech.Eng.312,428–446(2016)

39.Xu,B.X.,Zhao,Y.,Stein,P.:Phase field modeling of electrochemically induced fracture in Li-ion battery with large deformation and phase segregation.GAMM-Mitt.39,92–109(2016)

40.Newman,J.,Tobias,C.:Theoretical analysis of current distribution in porous electrodes.J.Electrochem.Soc.109,1183–1191(1962)

41.Newman,J.,Tiedemann,W.:Porous-electrode theory with battery applications.AIChE.J.21,25–41(1975)

42.Christensen,J.:Modeling diffusion-induced stress in Li-ion cells with porous electrodes.J.Electrochem.Soc.157,A366–A380(2010)

43.Lai,W.,Ciucci,F.:Mathematical modeling of porous battery electrodes—Revisit of Newman’s model.Electrochim.Acta 56,4369–4377(2011)

44.Landstorfer,M.,Jacob,T.:Mathematical modeling of intercalation batteries at the cell level and beyond.Chem.Soc.Rev.42,3234–3252(2013)

45.Zheng,J.P.,Crain,D.J.,Roy,D.:Kinetic aspects of Li intercalation in mechano-chemically processed cathode materials for lithium ion batteries:electrochemical characterization of ballmilled LiMn2O4.Solid State Ion.196,48–58(2011)

46.Chung,D.W.,Shearing,P.R.,Brandon,N.P.,et al.:Particle size polydispersity in Li-ion bateries.J.Electrochem.Soc.161,A422–A430(2014)

47.Wu,W.,Xiao,X.,Wang,M.,et al.:A microstructural resolved model for the stress analysis of lithium-ion batteries.J.Electrochem.Soc.161,A803–A813(2014)

48.Jokar,A.,Rajabloo,B.,Désilets,M.,et al.:Review of simplified pseudo-two-dimensional models of lithium-ion batteries.J.Power Sources 327,44–55(2016)

49.Aberg,S.:A simple model for the measurement of charge transfer resistances of reactions with slow kinetics.J.Electroanal.Chem.439,63–71(1997)

50.Zhang,X.,Shyy,W.,Sastry,A.M.:Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles.J.Electrochem.Soc.154,A910–A916(2007)

51.Zhang,X.,Sastry,A.M.,Shyy,W.:Intercalation-induced stressand heat generation within single lithium-ion battery cathode particles.J.Electrochem.Soc.155,A542–A552(2008)

52.Guo,Z.,Zhu,J.,Feng,J.,et al.:Direct in situ observation and explanation of lithium dendrite of commercial graphite electrodes.RSC Adv.5,69514–69521(2015)

53.Yang,L.,Yan,Y.,Ran,Z.,et al.:A new method for generating random fibre distributions for fibre reinforced composites.Compos. Sci.Technol.76,14–20(2013)

54.Takahashi,K.,Srinivasan,V.:Examination of graphite particle cracking as a failure mode in lithium-ion batteries:a model experimental study.J.Electrochem.Soc.162,A635–A645(2015)

55.Takahashi,K.,Higa,K.,Mair,S.,et al.:Mechanical degradation of graphite/PVDF composite electrodes:a model-experimental study.J.Electrochem.Soc.163,A385–A395(2016)

56.Orvananos,B.,Malik,R.,Yu,H.C.,et al.:Architecture dependence on the dynamics of nano-LiFePO4electrodes.Electrochim.Acta 137,245–257(2014)

57.Elul,S.,Cohen,Y.,Aurbach,D.:The influence of geometry in 2D simulation on the charge/discharge processes in Li-ion batteries.J.Electroanal.Chem.682,53–65(2012)

58.Jung,S.,Jung,H.Y.:Charge/discharge characteristics of Li-ion batteries with two-phase active materials:a comparative study of LiFePO4and LiCoO2cells.Int.J.Energy Res.40,1541–1555(2016)

59.Lim,C.,Yan,B.,Kang,H.,et al.:Analysis of geometric and electrochemical characteristics of lithium cobalt oxide electrode with different packing densities.J.Power Sources 328,46–55(2016)