GLOBAL STABILITY ANALYSIS FOR THE SINGLE-SPECIES ECOLOGICAL MODEL WITH THE DISPERSAL AND DISCONTINUOUS CONTROL TERM BASED ON THE THRESHOLD POLICY
GAO Yang
(Teacher Education College,Daqing Normal University,Daqing 163712,China)
1 Introduction
The study on the patch models became one central issue of concerns in the literature of ecology systems(see[1–5]),since it is an interesting problem to consider how the dispersal or migration of the species influences the global dynamics of the interacting ecological system.
Since the systems of discrete patchy models are usually high-dimensional,it is rather a challenge to study the uniqueness and stability of the positive equilibrium for patchy models from the mathematical aspect.The availably global dynamics criteria in the literatures mainly focus on the special case of two-patch(see[2])or the permanence and existence of periodic solutions(see[3–6]).
Recently,Li and Shuai(see[6])considered the following system that described growth and dispersal of a single species amongnpatches(n≥2),herexi∈R+represents population density of the species on patchi.fi∈C1(R+,R)represents the density dependent growth rate on patchi.Constantdij≥0 is the dispersal rate from patchjtoi,and constantαij≥0 can be selected to represent different boundary condition.
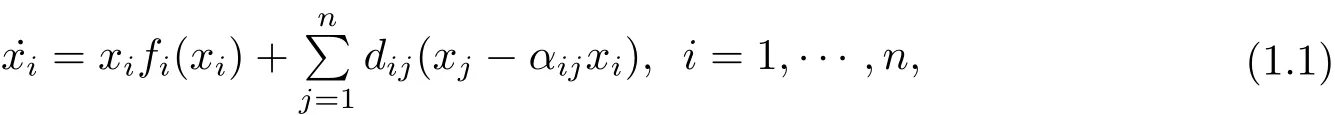
In[6],the authors studied the global stability of the coexistence equilibrium of system(1.1)by considering it as a couplednsub-models on networks.A systematic approach to construct global Lyapunov functions for large-scale coupled systems was developed.Li and Shuai obtained the following sharp result for system(1.1).
Proposition 1(see[6,Theorem 5.1])Assume that the following assumptions hold.
(1)(dij)n×nis irreducible.
(3)System(1.1)is uniformly persistent.
(4)Solutions of system(1.1)are uniformly ultimately bounded.
Then system(1.1)has a positive equilibriumE?∈Rn+which possesses globally asymptotical stability.
Although well-improved results were obtained in the above work on the single-species model with the dispersal,the model is not well studied when the discontinuous control is considered.In this paper,we will use a so-called threshold policy(TP)to control the single-species system.
In the context of fishing management,Collie and Spencer(see[8])introduced a so-called threshold policy(TP),which was intermediate between the well-known constant escapement and constant harvest rate policies.A TP is defined as follows:if estimated species abundance is below a previously chosen threshold level,harvesting is suppressed;above the threshold,harvesting is applied.TP is also an alternative strategy used in systems such as terrestrial harvesting(see[11]),grazing(see[12])and control of aquatic vegetation(see[13])etc.
A lot of researchers were interested in the threshold policy in the recent years(see[14–20,38–41]).In 2000(see[14]),authors analyzed the dynamics of two predator-prey models(Lotka-Volterra and Leslie-Gower)via the weighted escapement policy.In 2005(see[15]),stability of predator-prey models with TP was studied by using the idea of backstepping and control Lyapunov functions(CLF).In 2010(see[16]),the concept of virtual equilibria was used to design three different kinds of threshold policies.In 2011(see[17]),yield and related economic items generated by a TP were studied.In 2012(see[18]),a specific management strategy was proposed in order to control pests.In 2013(see[19]),a specific threshold policy was designed in order to control plant diseases and eventually maintain the number of infected plants below an economic threshold.In 2014(see[20]),a Filippov epidemic model with media coverage was proposed to describe the real characteristics of media/psychological impact in spread of the infectious disease.Mathematical bifurcation analyses with regard to the local,global stability of equilibria and local sliding bifurcations were performed.
In this paper,the single-species ecological system with the dispersal amongnpatches is studied.The specific TP is designed to control the increasing of the single species on patchk.
In this part,we will generalize model(1.1)into the new model(1.2).
First of all,the assumptions of model(1.2)are listed as follows.
(1)xi∈R+represents population density of the species on patchi.
(2)fi∈C1(R+,R)represents the density dependent growth rate on patchi.
(3)Constantdij≥0 is the dispersal rate from patchjtoi,and constantαij≥0 can be selected to represent different boundary condition.
(4)θk>0 represents the roguing proportional of the species on patchk.
Second,the control aim is listed as follows.
The Control Aim Through controlling the population density ofkth patch less thanETvia the TP

the number of species on each patch will be eventually stable at some corresponding positive value.
Therefore,the following single-species ecological model with the dispersal and discontinuous control term is constructed,

The network method was applied widely in recently years(see[22–30,35–37]).In this paper,we interpret system(1.2)as a coupled system on a network.Using the method of Li and Shuai[6]and Filippov system theory,we prove positive equilibrium’s existence theorems and global stability theorems.
A mathematical description of a network is a directed graph consisting of vertices and directed arcs connecting them.At each vertex,the local dynamics are given by a system of differential equations called the vertex system.The directed arcs indicate inter-connections and interactions among vertex systems.
A digraphGwithnvertices for system(1.2)can be constructed as follows.Each vertex represents a patch and(j,i)∈E(G)if and only ifdij>0,hereE(G)denotes the set of arcs(i,j)leading from inial vertexito terminal vertexj.At each vertex ofG,the vertex dynamics are described by a system
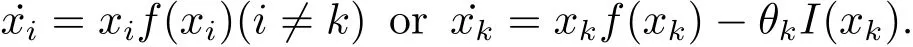
The coupling among system(1.2)is provided by dispersal of species among patches.The dispersal networkGis strongly connected if and only if the dispersal matrix(dij)n×nis irreducible.
From the ecology viewpoint,when the population density of the species on patchkexceedsET,then the control is implemented to reduce the population density of the species on patchk.While,when the population density of the species on patchkis less thanET,it is not necessary to implement control.
Remark 1 The term ofθkxkcomes from Zhao(see[19]).
On one hand,the value of the roguing rateθkis dependent on the number of available workers.
On the other hand,such a roguing term is reasonable in mathematics.
Remark 2 It is natural and reasonable to adopt the threshold policy in order to control the population density of the species on some patch.Besides,the control cost is reasonable.
Our contribution is listed as follows.
(1)Existence conditions of positive equilibria for system(1.2)are obtained by the uniform persistence theory and Filippov theory.
(2)Suffcient conditions that the positive coexistence equilibrium of the coupling model is unique and globally asymptotically stable are derived by using the method of constructing Lyapunov functions based on graph-theoretical approach for coupled systems.
This paper is organized as follows.We introduce preliminary results on graph theory based on coupled network models in Section 2.In Section 3,we obtain main results.Finally,the conclusions and outlooks are drawn in Section 4.
2 Preliminaries
In this section,we will list some definitions and theorems which will be used in the later sections.
A directed graph or digraphG=(V,E)contains a setV={1,2,···,n}of vertices and a setEof arcs(i,j)leading from initial vertexito terminal vertexj.A subgraphHofGis said to be spanning ifHandGhave the same vertex set.A digraphGis weighted if each arc(j,i)is assigned a positive weight.aij>0 if and only if there exists an arc from vertexjtoiinG.
The weightw(H)of a subgraphHis the product of the weights on all its arcs.A directed pathPinGis a subgraph with distinct verticesi1,i2,···,imsuch that its set of arcs is{(ik,ik+1):k=1,2,···,m}.Ifim=i1,we callPa directed cycle.
A connected subgraphTis a tree if it contains no cycles,directed or undirected.
A treeTis rooted at vertexi,called the root,ifiis not a terminal vertex of any arcs,and each of the remaining vertices is a terminal vertex of exactly one arc.A subgraphQis unicyclic if it is a disjoint union of rooted trees whose roots form a directed cycle.
Given a weighted digraphGwithnvertices,the weight matrixA=(aij)n×ncan be defined by their entryaijequals the weight of arc(j,i)if it exists,and 0 otherwise.For our purpose,we denote a weighted digraph as(G,A).A digraphGis strongly connected if,for any pair of distinct vertices,there exists a directed path from one to the other.A weighted digraph(G,A)is strongly connected if and only if the weight matrixAis irreducible.
The Laplacian matrix of(G,A)is denoted byL.Letcidenote the cofactor of thei-th diagonal element ofL.The following results are listed.
Theorem 2.1[6]Assumen≥2.Then
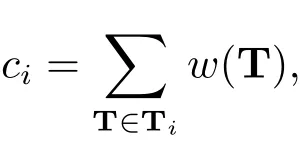
whereTiis the set of all spanning trees T of(G,A)that are rooted at vertexi,andw(T)is the weight ofT.In particular,if(G,A)is strongly connected,thenci>0 for 1≤i≤n.
Theorem 2.2[6]Assumen≥2.Letcibe given in Theorem 2.1.Then the following identity holds
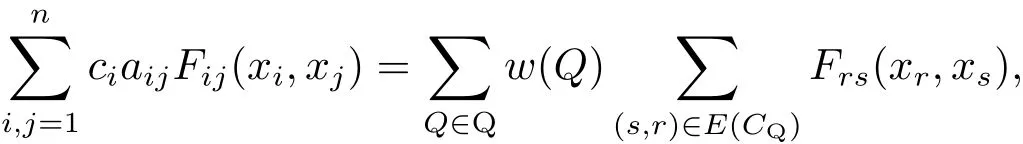
hereFij(xi,xj),1≤i,j≤n,are arbitrary functions,Qis the set of all spanning unicyclic graphs of(G,A),w(Q)is the weight ofQ,andCQdenotes the directed cycle ofQ.
Given a network represented by digraphGwithnvertices(n≥2),a coupled system can be built onGby assigning each vertex its own internal dynamics and then coupling these vertex dynamics based on directed arcs inG.Assume that each vertex dynamics are described by a system of differential equations=fi(t,ui),whereui∈Rmiandfi:R×Rmi→Rmi.Letgij:R×Rmi×Rmj→Rmirepresent the in fl uence of vertexjon vertexi,andgij≡0 if there exists no arc fromjtoiinG.Then we obtain the following coupled system on graphG:
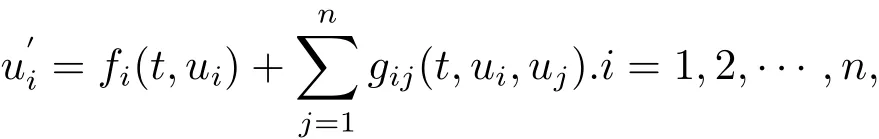
here we assume that the initial-value problem has the unique solution.
We assume that each vertex system has a globally stable equilibrium and possesses a global Lyapunov functionVi.
Theorem 2.3[6]Assume that the following assumptions are satis fi ed.
(1)There exist functionsVi(t,ui),Fij(t,ui,uj),and constantsaij≥0 such that
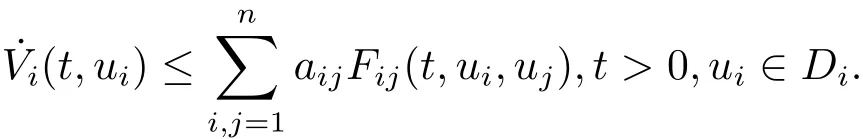
(2)Along each directed cycleCof the weighted digraph(G,A),A=(aij),
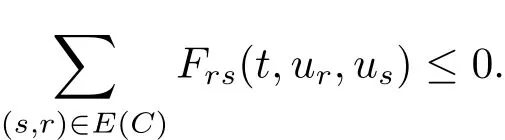
(3)Constantciis given by the cofactor of thei-th diagonal element ofL.Then the functionV(t,u)=satisfiesV˙(t,u)≤0 fort>0,andu∈D=D1×D2···×Dn.Namely,Vis a Lyapunov function for the system.
3 Main Results
Filippov solutions will be used for the discontinuous system(1.2).Consider the differential inclusion as follows
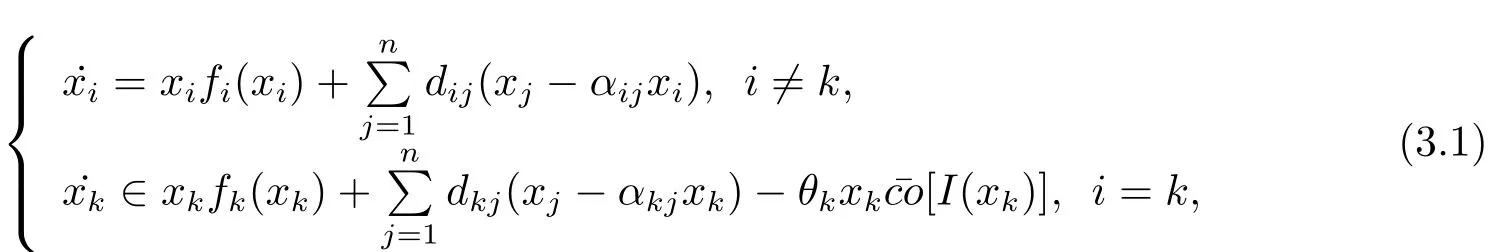
Definition 1x(t)=(x1(t),x2(t),···,xn(t))is the solution of system(1.2)with initial valuex1(0)=x10,x2(0)=x20,···,xn(0)=xn0,if
(1)x(t)is defined in the interval[0,T)withT∈(0,+∞].
(2)x(t)is absolutely continuous in any subinterval of[0,T).
(3)x(t)is the solution of system(3.1)for a.e.t∈[0,T).
We assume thatx?=is a positive equilibrium of system(1.2).By system(3.1)and measurable selection theorem(see[21]),there issuch that
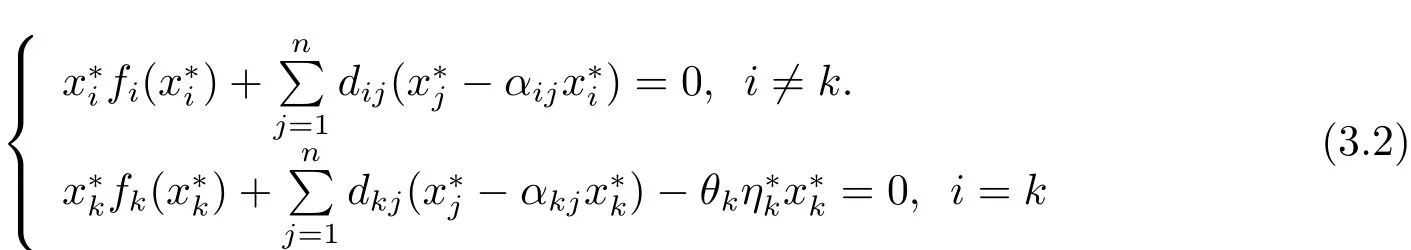
for a.e.t∈[0,T).
In this section, first of all,the existence of the positive equilibrium for system(1.2)is shown.The uniform persistence theory and Filippov theory are used to discuss the problem.Secondly,suffcient conditions that the positive coexistence equilibrium of the coupling model is unique and globally asymptotically stable inRn+as long as it exists are derived by using the method of constructing Lyapunov functions based on graph-theoretical approach for coupled systems.
3.1 The Existence Conditions of the Positive Equilibrium for System(1.2)
DefineA1(x)=diag[f1(x1),f2(x2),···,fn(xn)]and
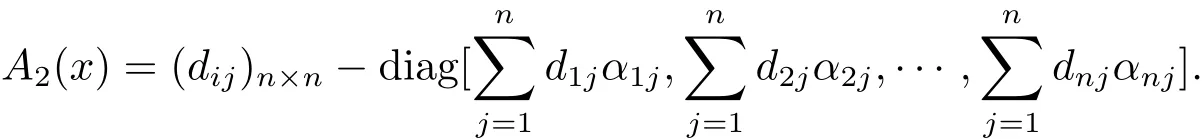
Then we obtain that the existence theorem for positive solutions of system(1.2).
Theorem 3.1 The solutionx(t)of system(1.2)satisfies that?t∈[0,t0),x(t)>0,if it is defined in the interval[0,t0)(0<t0≤+∞)and the initial value satisfies that
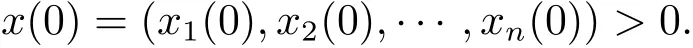
Proof By the definition ofI(xk),there existsδ>0(δ<ET),such that when|xk|<δ,I(xk)=0 holds.Considerx(t)withx(0)>0 and||x(t)||<δ,then system(1.2)can be simplified as follows˙x=[A1(x)+A2(x)]x.In the sequel,we deduce thatx(t)=x0exp[A1(x)+A2(x)]t.Therefore,we obtain thatx(t)>0,ifx(0)>0 and||x(t)||<δ.
By applying the absolutely continuous character of the solutions,it follows that?t∈[0,t0),x(t)>0 holds.This completes the proof.
Now we will consider the existence conditions for the equilibrium of system(1.2).The theorem is listed as follows.
Theorem 3.2 Assume that the following assumptions hold for system(1.1).(1)The system is uniformly persistent.
(2)Solutions are uniformly ultimately bounded.
Then system(1.2)has one positive equilibrium at least,if the suitableETis chosen.
Proof Using the Theorem 5.1 of Li and Shuai[6],we obtain that system(1.1)has one equilibrium at least.Letx?=denote the positive equilibrium of system(1.1).Then by choosingwe have{0}∈Therefore,we can chooser?=0∈such thatxifi(xi)(xj?αijxi)=0 fori=1,2,···,n.It means thatx?is the positive equilibrium of system(1.2).This completes the proof.Given the following system
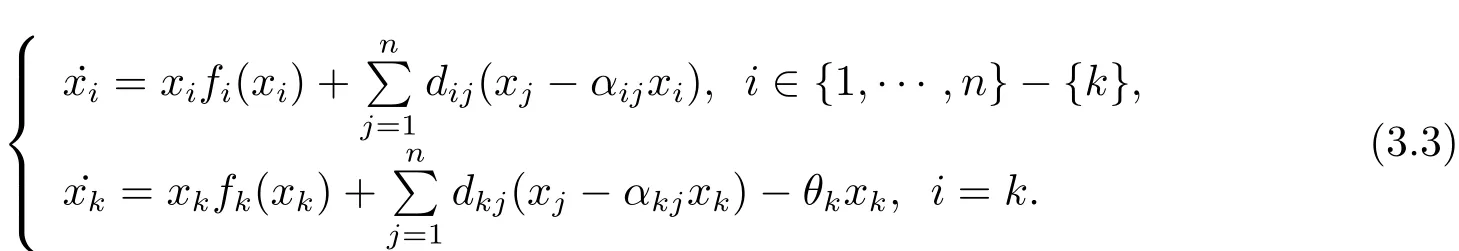
Using the uniformly persistence theory(see[34])and Theorem 3.2,the corollary is obtained naturally.
Corollary 1 Assume that the following assumptions hold for system(3.3).(1)The system is uniformly persistent.
(2)Solutions are uniformly ultimately bounded.
Then system(1.2)has one positive equilibrium at least,if the suitableETis chosen.
3.2 The Stability Analysis of the Positive Equilibrium for System(1.2)
Similar to system(3.1),whenx(t)=(x1(t),x2(t),···,xn(t))is the solution of system(1.2),then for anyv,there is a measurable functionηk(t)∈(measurable selection theorem(see[21]))such that
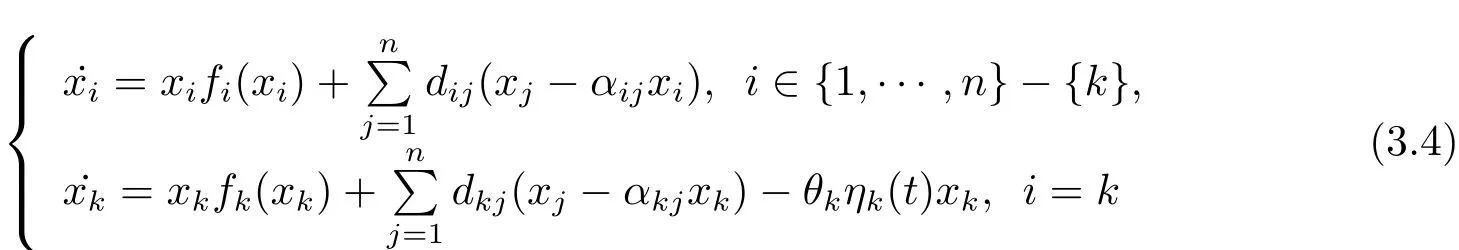
for a.e.t∈[0,T).
The main result is listed as follows.
Theorem 3.3 Assume that the following assumptions hold.
(3)There exists a positive equilibriumx?=for system(1.2).Then positive equilibriumx?of system(1.2)is unique and globally asymptotically stable inRn+.
Proof After tedious calculation,we obtain that the positive equilibriumx?satisfies
(1)(dij)n×nis irreducible.
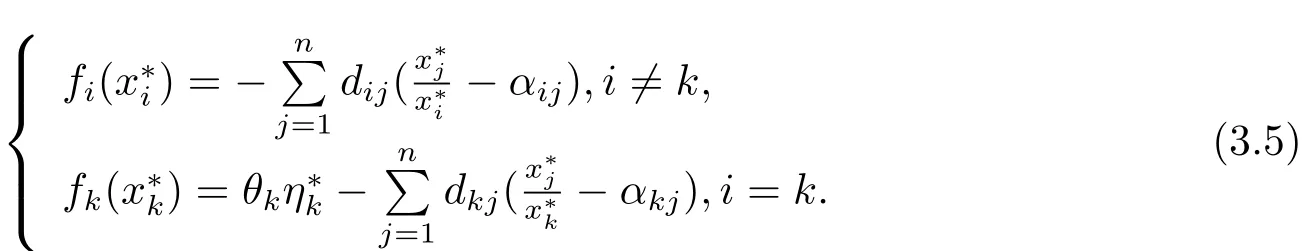
SetVi(xi)=It can be verified thatVi(xi)>0 for allxi>0 andVi(xi)=0 if and only ifAfter direct calculation,we have(i/=k)
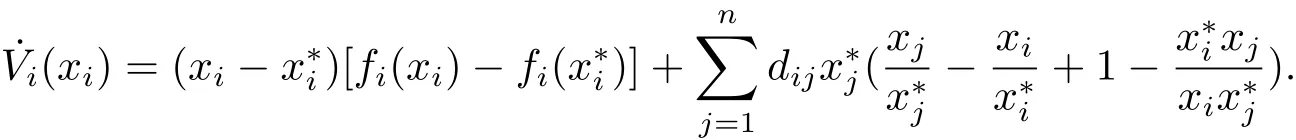
Letaij=Then we obtain that˙Vi(xi)and
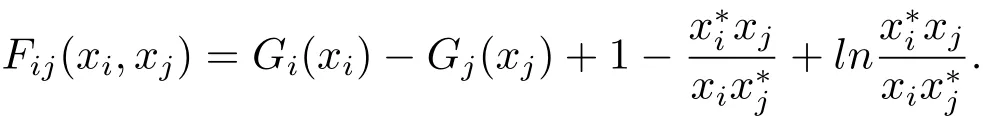
In the sequel,we obtain thatFij(xi,xj)≤Gi(xi)?Gj(xj).Wheni=k,we have
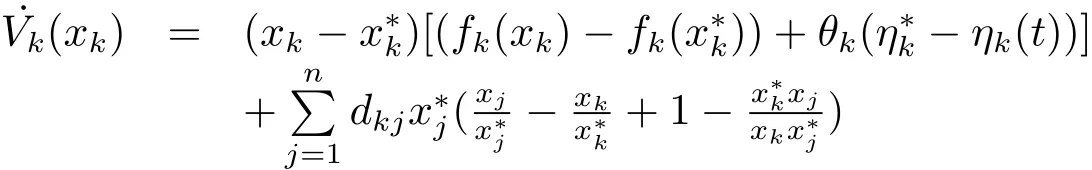
for a.e.t∈[0,T).
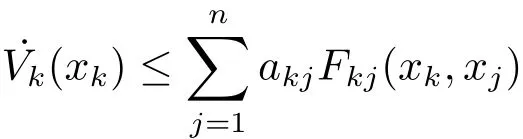
for a.e.t∈[0,T).
Letcidenote the cofactor of thei-th diagonal element of Laplacian Matrix ofG.Let Lyapunov functionV(x)=V(x1,x2,···,xn)Then we haveV˙(x(t))≤0 for a.e.t∈[0,T).If˙V=0,we obtain that=0 for a.e.t∈[0,T).Therefore,we deduce thatfor a.e.t∈[0,T).By applying the absolutely continuous character of the solutions,it follows thatBy using the strong connectivity of(G,A)and
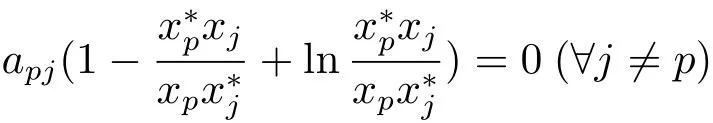
for a.e.t∈[0,T),we obtain thatfor a.e.t∈[0,T).By applying the absolutely continuous character of the solutions andit follows thatfor anyj=1,2,···,n.Furthermore,we obtain that the maximum weak invariant subset ofis the set of unique pointM={x?}.By applying the invariance principle of differential inclusion(see[21]),we obtain thatx?is globally asymptotically stable inHere
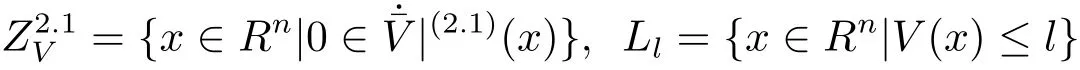
and
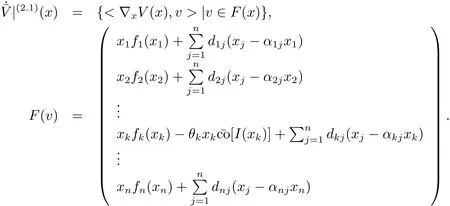
This completes the proof.
Furthermore,the control can be used on all of patches for system(1.1).Consider the following system
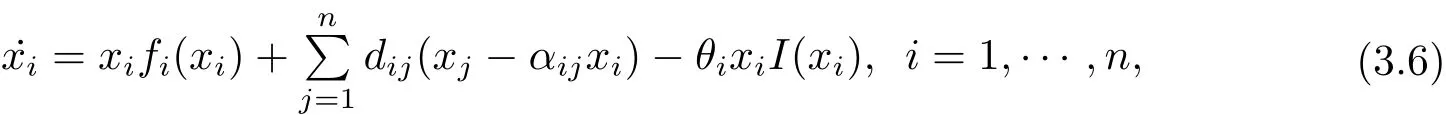
here
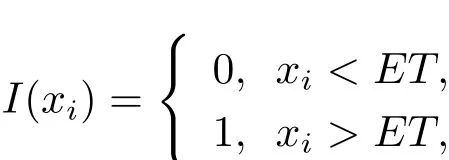
θi>0 represents the roguing proportional for the species on theith patch.
In the sequel,Corollary 2 is obtained.
Corollary 2 Assume that the following assumptions hold.
(1)(dij)n×nis irreducible.
(3)There exists a positive equilibriumx?=(x?1,x?2,···,x?n)for system(3.6).Then positive equilibriumx?of system(3.6)is unique and globally asymptotically stable inRn+.
Remark 3 Corollary 2 can be seen as the development of the Theorem 2.3.It means that network method can be applied in the Filippov system.
4 Conclusions and Outlooks
In this paper,we generalize the single-species ecological model(1.1)to the general model(1.2)with the discontinuous control term for thekth patch.Firstly,the uniform persistence and Filippov theory are used to prove the existence of positive equilibrium.We obtain the existence condition for the positive equilibrium which can be seen as the development of the Theorem 5.1 in[6].Second,the globally asymptotical stability of positive equilibria of system(1.2)and(2.6)is proved based on the network method for coupled systems of differential equations,Filippov theory and differential inclusion.Our main theorems generalize Theorem 5.1 and 3.1 in[6].
Biologically,our result Theorem 3.3 implies that,if we consider to control the population density ofkth patch less thanETby using the TP,the single-species ecological model with dispersal is dispersing among strongly-connected patches(which is equivalent to the irreducibility of the dispersal matrix),and if the system has an equilibrium at least,then the number of species in each patch will be eventually stable at some corresponding positive value.
Further studies on this subject are being carried out by the presenting authors in the two aspects:one is to study the TP with time delay;the other is to discuss the method to design control term via the TP.
[1]Freedman H I,Takeuchi Y.Global Stability and predator dynamics in a model of prey dispersal in a patchy environment[J].Nonl.Anal.-The.Meth.Appl.,1989,13(8):993–1002.
[2]Kuang Y,Takeuchi Y.Predator-prey dynamics in models of prey dispersal in 2-patch environments[J].Math.Biosci.,1994,120(1):77–98.
[3]Cui J G.The effect of dispersal on permanence in a predator-prey population growth model[J].Comput.Math.Appl.,2002,44(8-9):1085–1097.
[4]Xu R,Chaplain M A J,Davidson F A.Periodic solutions for a delayed predator-prey model of prey dispersal in two-patch environments[J].Nonl.Anal.-Real World Appl.,2004,5(1):183–206.
[5]Zhang L and Teng Z D.Permanence for a delayed periodic predator-prey model with prey dispersal in multi-patches and predator density-independent[J].J.Math.Anal.Appl.,2008,338(1):175–193.
[6]Li M Y,Shuai Z S.Global-stability problem for coupled systems of differential equations on networks[J].J.Diff.Equa.,2010,248(1):1–20.
[7]Li M Y,Shuai Z S.Global stability of an epidemic model in a patchy environent[J].Canad.Appl.Math.Quart.,2009,17:75–187.
[8]Collie J S,Spencer P D.Management strategies for fish populations subject to long term environmental variability and depensatory predation[J].Tech.Rep.93-02,Alaska Sea Grant College,1993,57:629–650.
[9]Quinn T J,Deriso R B.Quantitative fi sh dynamics,biological resource management series[M].Oxford:Oxford Univ.Press,2000.
[10]Loehle C.Control theory and the management of ecosystems[J].J.Appl.Ecol,2006,43:957–966.
[11]Jonz′en N,Ranta E,Lunberg P,Kaitala V,Linden H.Harvesting induced fl uctuations[J].Wild.Biol.,2003,9:59–65.
[12]Noy-Meir I.Stability of grazing systems:an application of predator–prey graphs[J].J.Ecol.,1975,63(2):459–481.
[13]Van Nes E H,Scheffer M,Van den Berg M S,Coops H.Aquatic macrophytes:restore,eradicate or is there a compromise[J].Aquatic Bot.,2002,72(3-4):387–403.
[14]Costa M I S,Kaszkurewicz E,Bhaya A,Hsu L.Achieving global convergence to an equilibrium population in predator-prey systems by the use of discontinuous harvesting policy[J].Ecolo.Model.,2000,128:89–99.
[15]Meza M E M,Bhaya A,Kaszkurewicz E,Costa M I S.Threshold policies control for predator-prey systems using a control Lyapunov function approach[J].The.Popul.Bio.,2005,67(4):273–284.
[16]Meza M E M,Bhaya A.Control theory and the management of ecosystems:A threshold policy with hysteresis is robust[J].Appl.Math.Comput.,2010,216:31–33.
[17]Meza M E M,Costa M I S.Exploitation of a single species by a threshold management policy[J].Math.Biosci.,2011,234:25–32.
[18]Tang S Y,Liang J H,Xiao Y N,Cheke R A.Sliding bifurcation of Filippov two stage pest control models with economic thresholds[J].SIAM J.Appl.Math.,2012,72:1061–1080.
[19]Zhao T T,Xiao Y N,Smith R J.Non-smooth plant disease models with economic thresholds[J].Math.Biosci.,2013,241:34–48.
[20]Wang A L,Xiao Y N.A Filippov system describing media effects on the spread of Infectious diseases[J].Nonl.Anal.:Hybrid Sys.,2014,11:84–97.
[21]Huang L H,Guo Z Y,Wang F J.The theory and application for the differential equations with discontinuous right side(in Chinese)[M].Beijing:Sci.Press,2013.
[22]Guo H,Li M Y,Shuai Z.A graph-theoretic approach to the method of global Lyapunov functions[J].Proc.Amer.Math.Soc.,2008,136:2793–2802.
[23]Olfati-Saber R.Flocking for multi-agent dynamic systems:algorithms and theory[J].IEEE Trans.Auto.Contr.,2006,51:401–420.
[24]Moshtagh N,Jadbabaie A,Daniilidis K.Distributed geodesic control laws for fl ocking of nonholonomic agents[C].Proc.44th IEEE Conf.Dec.Contr.,2005 and 2005 Eur.Contr.Conf.(CDCECC’05),2005:2835–2841.
[25]Freeman R A,Yang P,and Lynch K M.Distributed estimation and control of swarm formation statistics[C].Proc.2006 Am.Contr.Conf.,2006:749–755.
[26]Hong Y G,Gao L X,and Cheng Z D,Hu J P.Lyapunov-based approach to multi-agent systems with switching jointly connected interconnection[J].IEEE Trans.Auto.Contr.,2007,52(5):943–948.
[27]Olfati-Saber R,Shamma J S.Consensus filters for sensor networks and distributed sensor fusion[C].44th IEEE Conf.Dec.Contr.,2005 and 2005 Eur.Contr.Conf.(CDC-ECC’05),2005:6698–6703.
[28]Hagan M T,Demuth H B,Beale M H.Neural network design[M].Beijing:China Machine,2002.
[29]Zhou Z H,Cao C G.Neural network with applications[M].Beijing:Tsinghua Univ.Press,2004.
[30]Cheng H,Juan Y,Jiang H J,Teng Z D.Exponential stabilization and synchronization of neural networks with time-varying delays via periodically intermittent control[J].IOP Publ.Nonl.,2010,23:2369–2391.
[31]Khalil H K.Nonlinear systems(3rd ed.)[M].New Jersey:Prentice Hall,2002.
[32]Hirsch M W,Smith H L,Zhao X Q.Chain transitivity,attractivity,and strong repellors for semidynamical systems[J].J.Dynam.Diff.Equa.,2001,13:107–131.
[33]Freedman H I,Tang M X,Ruan S G.Uniform persistence and fl ows near a closed positively invariant set[J].J.Dynam.Diff.Equa.,1994,6:583–600.
[34]Wang W D,Zhao X Q.An epidemic model in a pathy environment[J].Math.Biosci.,2004,190:97–112.
[35]Gao Y,Liu S Q.Global Stability for a predator-prey model with dispersal among patches[J].Abstr.Appl.Anal.,2014,176493:1–6.
[36]Eze E C,Zhang S J,Liu E J,Eze J C.Advances in vehicular adhoc networks(VANETs):challenges and road-map for future development[J].Intern.J.Auto.Comp.,2016,13:1–18.
[37]Ma K,Li L,Yang J,Liu Z X,Li X B,Guan X P.Bandwidth allocation with minimum rate constraints in cluster-based femtocell networks[J].Intern.J.Auto.Comp.,2015,12:77–82.
[38]Zhao T T,Xiao Y N.Plant disease models with nonlinear impulsive cultural control strategies for vegetatively propagated plants[J].Math.Comp.Simul.,2015,107:61–99.
[39]Zhang X H,Tang S Y.Existence of multiple sliding segments and bifurcation analysis of Filippov prey-predator model[J].Appl.Math.Comp.,2014,239:265–284.
[40]Kuang Y Q,Qiu M Q.Qualitative analysis of a class of predator-prey model with sublinear functional response function[J].J.Math.,2010,30(1):125–130.
[41]Ke Y S,Li B W,Chen B S.Hopf bifurcation of a delayed predator-prey model with stage structure for the predator[J].J.Math.,2015,35(2):252–266.
- 數(shù)學(xué)雜志的其它文章
- A NOTE ON HILBERT TRANSFORM OF A CHARACTERISTIC FUNCTION
- THE NEHARI MANIFOLD FOR A QUSILINEAR SUB-ELLIPTIC EQUATION WITH A SIGN-CHANGING WEIGHT FUNCTION ON THE HEISENBERG GROUP
- NOTES ON STRONGLY SEPARABLE EXTENSIONS
- EXISTENCE OF SOLUTIONS TO THE INITIAL VALUE PROBLEM OF SEMI-LINEAR GENERALIZED TRICOMI EQUATION
- SOME PROPERTIES IN THE GENERALIZED MORREY SPACES ON HOMOGENOUS CARNOT GROUPS
- A NONTRIVIAL PRODUCT OFIN THE COHOMOLOGY OF THE STEENROD ALGEBRA

