A NOTE ON HILBERT TRANSFORM OF A CHARACTERISTIC FUNCTION
QU Meng,JIANG Man-ru
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)
1 Introduction
The Hilbert transform is the operatorHdefined by
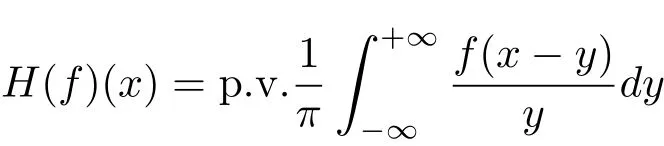
initially forf∈S(R).A very straight calculus via Fourier transform and Plancherel’s equality show thatHcan be extended to an isomorphic onL2;i.e.,

There were also several other ways to prove(1.1),see[2,7]and references therein.Halso satisfies so called Kolmogorov’s inequality;i.e.,for anyλ>0,there exists a positive constantCsuch that

The best possible constantCin(1.2)was obtained by Davis in[4].Moreover by interpolation technique and duality argument,Hcan be extended to a bounded operator onLp(R)for allp>1.We can refer to the nice textbooks[3,5]and[9]for more properties of Hilbert transform.
LetEbe a Lebesgue measurable set with|E|<∞and denoteH(χE)be the Hilbert transform of the characteristic function of the setE.In 1959,Stein and Weiss[8]proved that the distribution function ofH(χE)does not depend on the structure of the setEbut only on its measure|E|.More precisely,for anyλ>0,
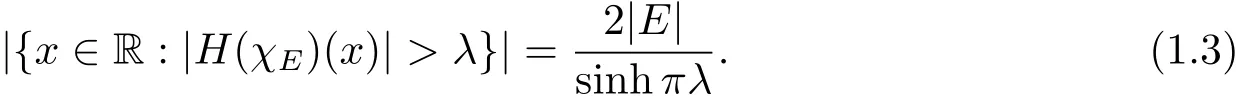
In[1],Colzani,Laeng and Monz′on gave an exact formula for theLpintegral ofH(χE).For 1<p<∞,
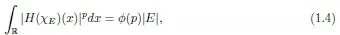

Theorem 1.1 LetEbe a Lebesgue measurable subset of R with|E|<∞and letHbe the Hilbert transform.For all 1<p<∞,
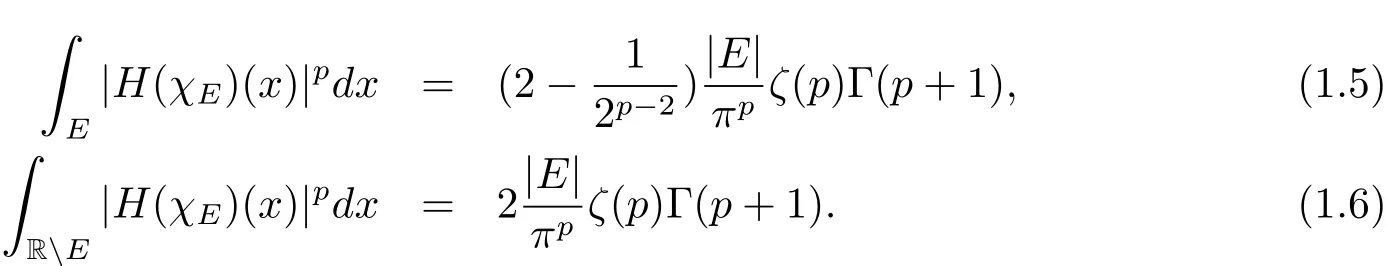
Theorem 1.2 LetEbe a Lebesgue measurable subset of R with|E|<∞and letHbe the Hilbert transform.For anyλ>0,
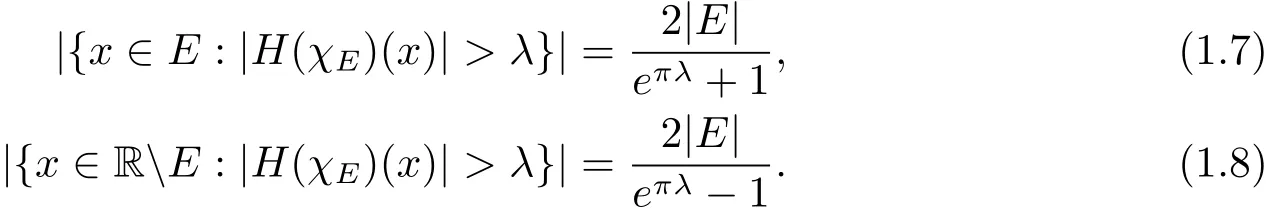
We note that in the proof of Theorem 1.2,Laeng used an argument taking Theorem 1.1 for granted.This argument(Lemma 1.4 in[1])reads
If‖f‖p=‖g‖pforp1<p<p2then the distrubtion functions offandgequals;i.e.,|{x∈E:|f(x)|>λ}|=|{x∈E:|f(x)|>λ}|for allλ>0.
Also as pointed in[1],this argument is based on a Mellin transform.However as in the usual way,theLp(X)norm has layer cake representation
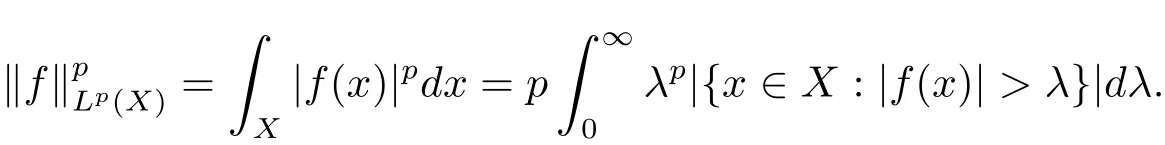
Once we proved the distribution function result(Theorem 1.2)in a direct way,Theorem 1.1 is proved with the help of“l(fā)ayer cake representation”.
This short note is just based on the upon argument.In Section 2,we prove Theorem 1.2 which relies on a refinement of the key lemma in[8]by Stein and Weiss.The proof of Theorem 1.2 also relies on a limiting argument.In Section 3,by using Theorem 1.2,we give the proof of Theorem 1.1 on the straight-forward way.
2 Proof of Theorem 1.2
We first recall the following result in[8].
Lemma 2.1 LetEbe a compact set in R withwherea1<b1<a2<b2<···<an<bn.Denotebe a rational function.Then for anyξ>1,
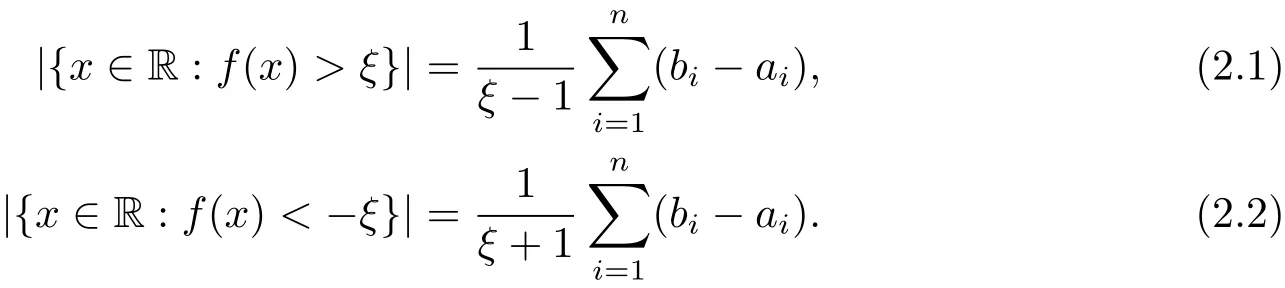
Remark 2.2 LetEas in Lemma 2.1,an observation is for anyξ>0,
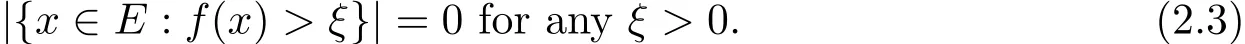
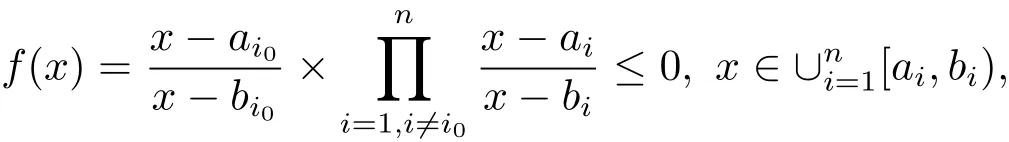
which implies that the set{x∈E:f(x)>ξ}is at most the collection of finite elementsb1,···,bnand then is a set of measure zero.
With(2.1)and(2.3),we immediately have
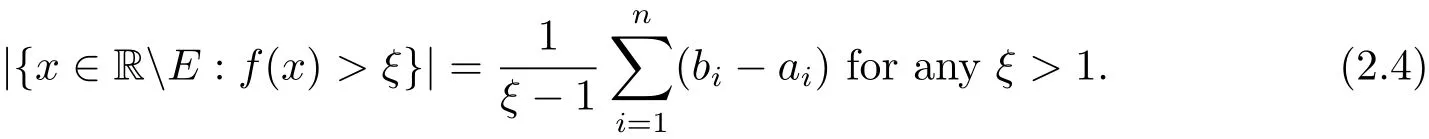
Similar way as discussed above,we also have
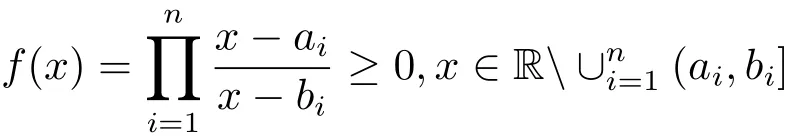
and

By(2.2)and(2.5),we have
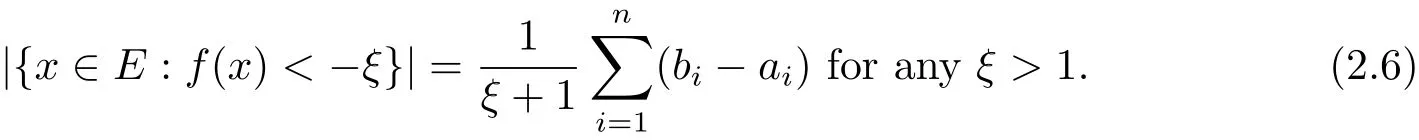
Similar to Lemma 2.1 and Remark 2.2,we immediate have
Lemma 2.3 LetEas in the Lemma 2.1.Denotewe have
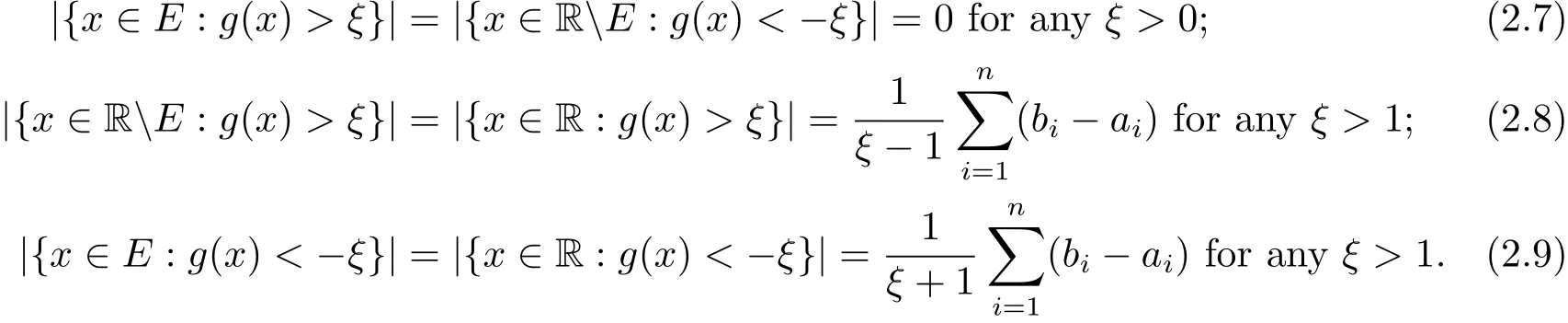
The following lemma asserts that Theorem 1.2 is right for a compact setE?R.
Lemma 2.4 LetEbe a compact set,equations(1.7)and(1.8)preserve.
Proof For any compact setE,we can writewitha1<b1<a2<b2<···<an<bn.De fi neandg(x)=as introduced in Lemma 2.1.By the property of Hilbert transformHχ[a,b](x)(see Example 5.1.3 in[5]),we have
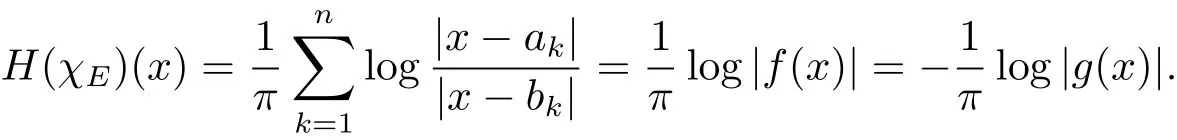
So for anyλ>0,the set{x∈R:|H(χE)(x)|>λ}can be rewrite as
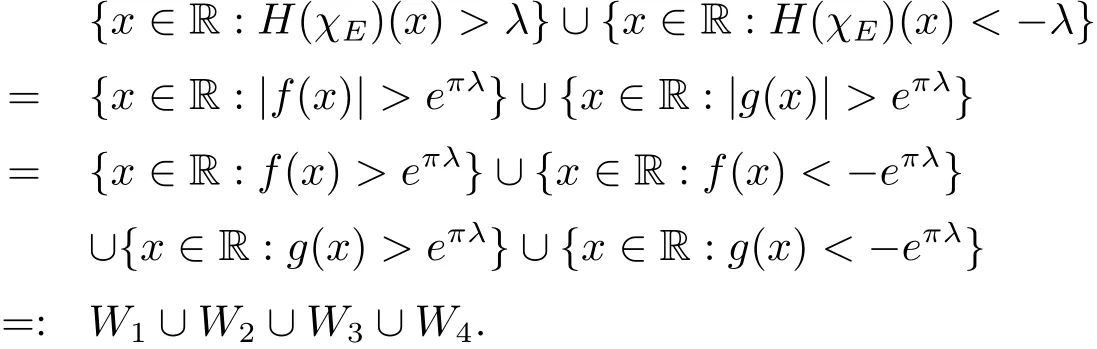
We note thatWiintersect empty each other.Therefore

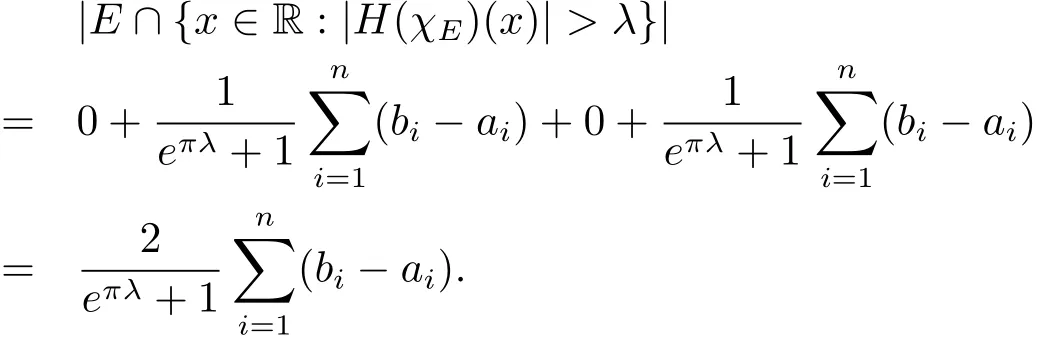
The same way,by(2.3),(2.5),(2.7)and(2.8)withξ=eπλ,
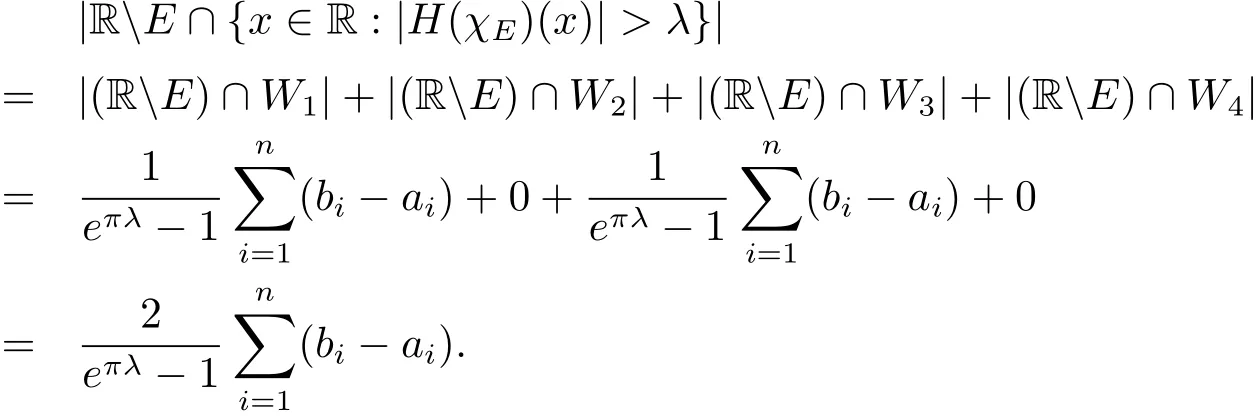
The lemma is proved.
Now we turn to the proof of Theorem 1.2.SinceEis finite measurable set,there exists a sequence of compact sets{Fn},suqch that for anyn,Fn?EandWith which we immediately getand then(1.1).Now for any fixedλ>0,we write
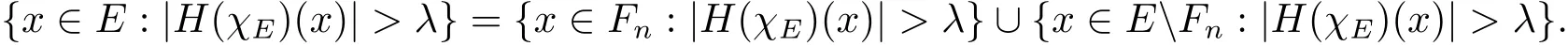
Then for anyu∈(0,1),by Chebyshev’s inequality and Lemma 2.4,we have
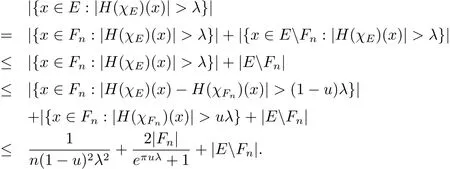
Letn→∞,and then letu→1,we have
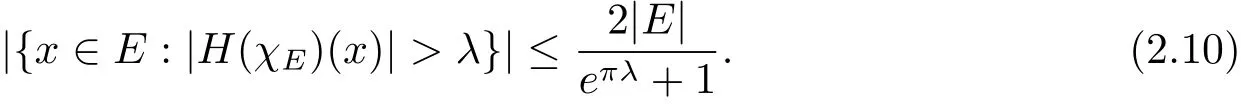
On the other hand,for anynand anyu∈(0,1),Chebyshev’s inequality and Lemma 2.4 gives
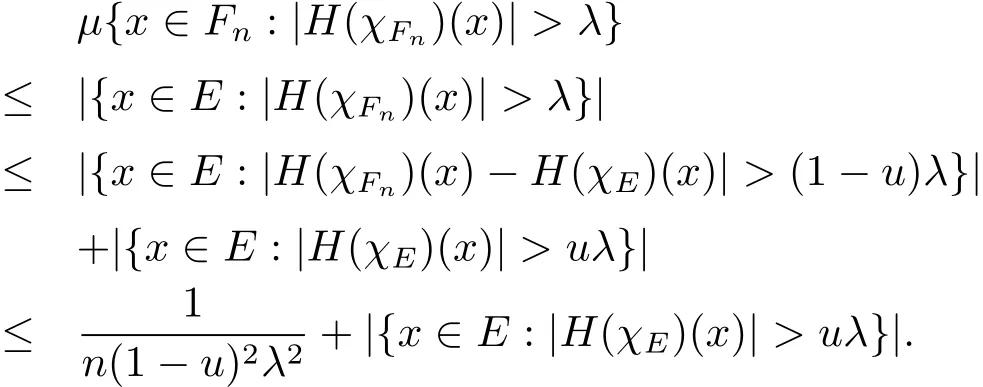
Letn→∞and then letu→1,we haveBoth(2.10)and(2.11)give|{x∈E:|H(χE)(x)|>λ}|This is just the equation(1.7).We end the proof of Theorem 1.2 since the proof of(1.8)is the similar one.
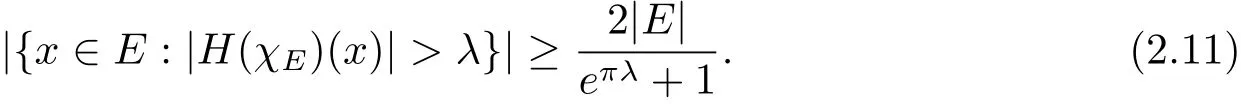
3 Proof of Theorem 1.1
Proof We only prove(1.5)since we can prove(1.6)in the similar way.Forp>1,
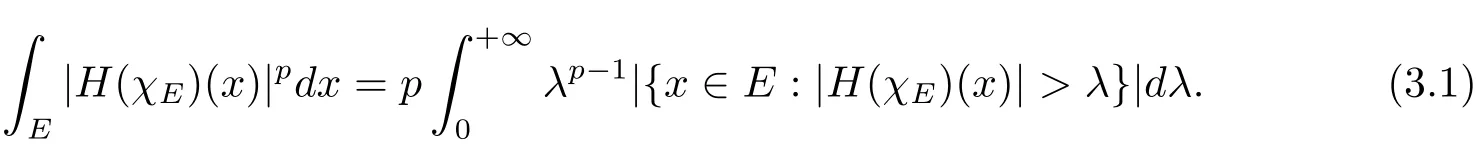
Then by Theorem 1.2,we have

and
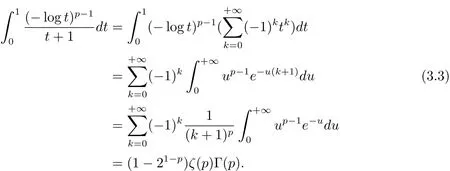
In the last equality in(3.3),we useCombining(3.1)–(3.3),(1.5)follows.
[1]Colzani L,Laeng E,Monz′on L.Variations on a theme of Boole and Stein-Weiss[J].J.Math.Anal.Appl.,2010,363:225–229
[2]Duoandikoetxea J.The Hilbert transform and Hermite functions:a real variabel proof of theL2-isometry[J].J.Math.Anal.Appl.,2008,347:592–596.
[3]Duoandikoetxea J.Fourier analysis[M].Providence,RI:American Math.Soc.,2001.
[4]Davis B.On the weak type(1,1)inequality for conjugate functions[J].P.Amer.Math.Soci.,1974,44:307–311.
[5]Grafakos L.Classical Fourier analysis(3nd ed.)[M].GTM 249,New York:Springer,2014.
[6]Laeng E.On theLpnorm of the Hilbert transform of a characteristic function[J].J.Func.Anal.,2012,262:4534–4539.
[7]Laeng E.A simple real-variable proof that the Hilbert transform is anL2-isometry[J].C.R.Math.Acad.Sci.Paris.,2010,348(17-18):977–980.
[8]Stein E,Weiss G.An extension of a theorem of Marcinkiewicz and some of its application[J].J.Math.Mech.,1959,8:263–284.
[9]Wei D.Boundedness of the Hilbert transform on Banach valued Hardy spaces[J].J.Math.,1999,19(1):117–120.
- 數(shù)學(xué)雜志的其它文章
- THE NEHARI MANIFOLD FOR A QUSILINEAR SUB-ELLIPTIC EQUATION WITH A SIGN-CHANGING WEIGHT FUNCTION ON THE HEISENBERG GROUP
- NOTES ON STRONGLY SEPARABLE EXTENSIONS
- EXISTENCE OF SOLUTIONS TO THE INITIAL VALUE PROBLEM OF SEMI-LINEAR GENERALIZED TRICOMI EQUATION
- SOME PROPERTIES IN THE GENERALIZED MORREY SPACES ON HOMOGENOUS CARNOT GROUPS
- A NONTRIVIAL PRODUCT OFIN THE COHOMOLOGY OF THE STEENROD ALGEBRA
- REGRESSION ANALYSIS OF CLUSTERED CURRENT STATUS DATA UNDER THE ADDITIVE HAZARDS MODEL

