Spatio-Temporal Deformation of Kink-Breather to the(2+1)-Dimensional Potential Boiti–Leon–Manna–Pempinelli Equation?
Li-Li Song(宋莉莉), Zhi-Lin Pu(蒲志林), and Zheng-De Dai(戴正德)School of Mathematics and Software Science,Sichuan Normal University,Chengdu 610068,China
2School of Mathematics and Statistics,Yunnan University,Kunming 650091,China
1 Introduction
The nonlinear evolution equation is one of the typical models that describes the complexity of nature,and it is better to approach the essence of object things,so the nonlinear evolution equation plays an important role in the nonlinear science field.It has broad prospect and widespread application foregrounds in some realm,such as fluid mechanics,quantum field theory,nonlinear optics,life science,communication and so on.To study nonlinear evolution equation,soliton theory is one of the most important methods.With the development of soliton theory,plenty of methods of solving soliton are put forward,for instance,the Darboux transformation method,[1?3]the Hirota bilinear method,[4?6]the Lie group method,[7?9]the homogeneous balance method,[10?11]the variable separation method,[12]the inverse scattering method,[13?15]symmetry reductions,[16?17]wronskian technique[18]etc.However,solving analytical solution of soliton dynamical systems is very diffcult,especially in the higher dimensional systems.Under these circumstances,what directly analyzing and observing the behavior of solitons is a necessary method to study soliton dynamical problem.Generally,soliton’s velocities,frequency and amplitude will not change after solitons’interaction.But when it meets some conditions,velocities,frequency and amplitude will alter,and one wave can even be drowned by another wave.In the paper,[19]the interaction between kinky solitary wave and rogue wave for(2+1)-dimensional Burgers equation is disscused,and it finds soliton fusion and fission phenomenon.And the other paper,[20]it researches the completely non-elastic interaction between kink wave and rational breather wave for(3+1)-dimensional potensional Yu–Toda–Sasa–Fukuyama equation,and it is found that rational breather wave is drowned or swallowed by kink wave.
In the paper,we consider the(2+1)-dimensional Boiti–Leon–Manna–Pempinelli(BLMP)equation as follows:

The equation(1)was most early proposed by Boiti et al.based on the relationship of weak Lax pair,and it can be regarded as asymmetrical form of the following Nizhnik–Novikov–Veselov equation in the space{x,y}.
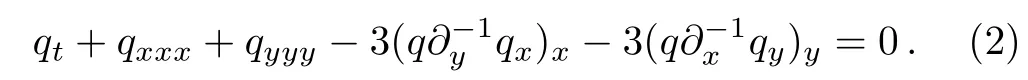
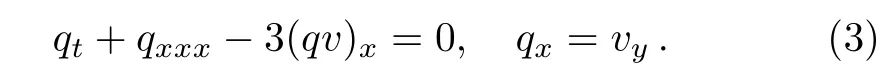
Using the potentialq=uygives the(2+1)-dimensional potential Boiti–Leon–Manna–Pempinelli(PBLMP)equation:
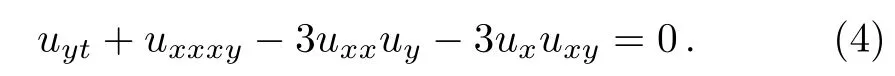
Some results of Eq.(4)have been released,for example,large of exact solutions have been gained by using variable separation method,[21?22]lie group method,[23]modified Clarkson–Krushal direct method[24]and so on.In the literature,[25]the conservation law and the correlation between symmetry and conservation law are given.The periodic-wave solutions for Eq.(4)appear in the literature.[26]However,spatio-temporal deformation of the solitary wave of the(2+1)-dimensional PBLMP equation have not been reported.In this paper,using the painleve analysis and Hirota bilinear method,we will gain the kink solitary wave and rational breather soliton of the(2+1)-dimensional PBLMP equation,and discuss their spatio-temporal deformation.Eventually,we find the fusion and degeneration of the kink solitary wave occur in this process.This is a very meaningful phenomena in researching soliton dynamical complexity in the higher dimensional system.
Now,we take the following four steps:
Step 1A transformationu=T(f)is made by Painleve analysis for some new and unknown function.
Step 2Using the transformationu=T(f)of step 1,the initial equation can be turned into the Hirota bilinear formG(Dt,Dx,Dy,f)=0,whereD-operator is defined by
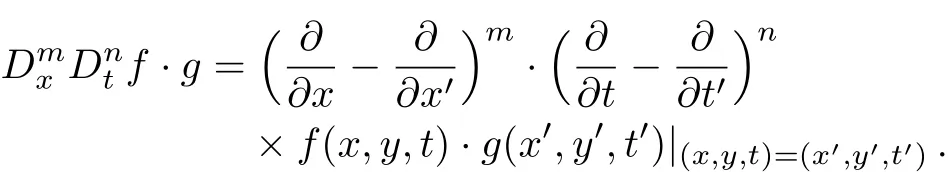
Step 3Solving the above equation to obtain kinkbreather by selecting the test function which comprises rational function and exponential function.
Step 4Under the condition of the non-singularity of kink-breather,we can get spatio-temporal deformation phenomenon at different times.
2 Kink Solitary Wave Solution
In the part,we will search for kink solitary wave solution of the(2+1)-dimensional PBLMP equation by means of Painleve analysis and Hirota bilinear method.Meanwhile,we will select suitable test function to help in the quest.
Using Painleve analysis in Eq.(4),let
3 Rational Breather Soliton
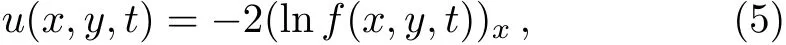
wheref(x,y,t)is unknown real function.Substituting Eq.(5)into Eq.(4),by the aid of the Hirota bilinear operatorD,we will get the following bilinear form:

that is
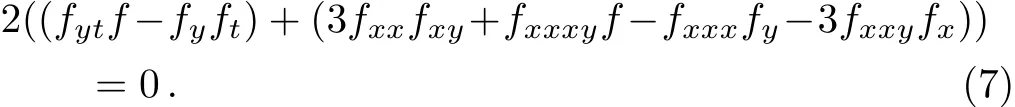
With regard to Eq.(6),we choose test function of the following form to seek for the kink solitary wave solution of(2+1)-dimensional PBLMP equation.

wherea3,b3andc3are real constants to be determined.
Substituting Eq.(8)into Eq.(6)we get
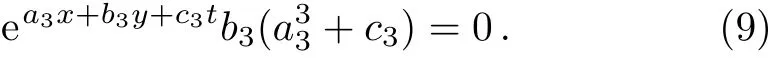
Thereby,we obtain the following dispersion relation from Eq.(9),

Meanwhile,we can also get the following solution of the(2+1)-dimensional PBLMP equation
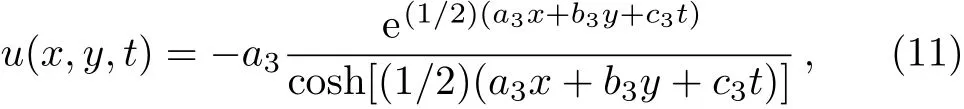
wherea3,b3andc3are contents related to the dispersion relation(10).Whent→ +∞,the solutionu→ ?2a3,and whent→ ?∞,the solutionu→ 0.So the solution(11)is the kink solitary wave solution(see Fig.1).
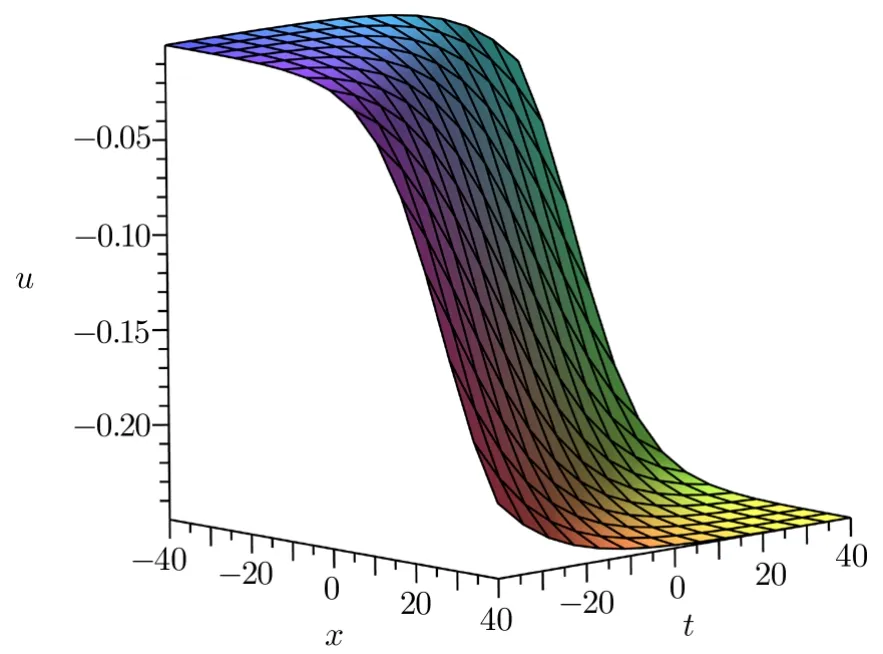
Fig.1 The kink solitary wave as a3=1/8,b3=0,and c3=1/12.
In the part,similarly,drawing support from the Hirota bilinear form and selecting the following test function to seek for the rational breather soliton of the(2+1)-dimensional PBLMP equation.
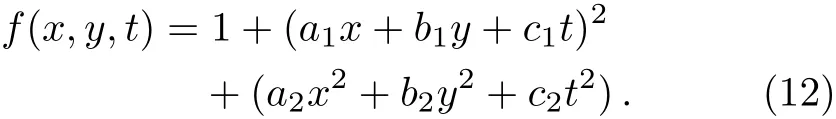
Plugging(12)into(6)with the help of Maple,and equating all coeffcient of all power ofx,y,t,we get the following algebraic equations.
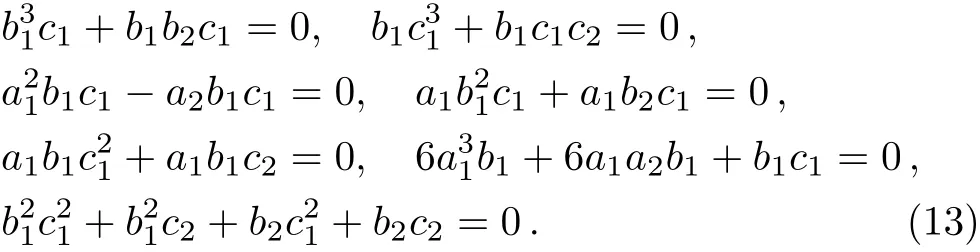
Solving algebraic Eqs.(13),we choose the following set of solutions
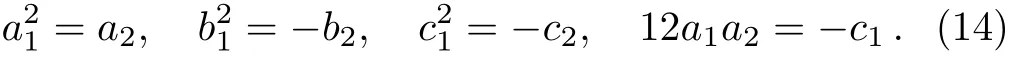
So we get the following rational breather soliton of the(2+1)-dimensional PBLMP equation by putting Eq.(14)and Eq.(12)into Eq.(5)
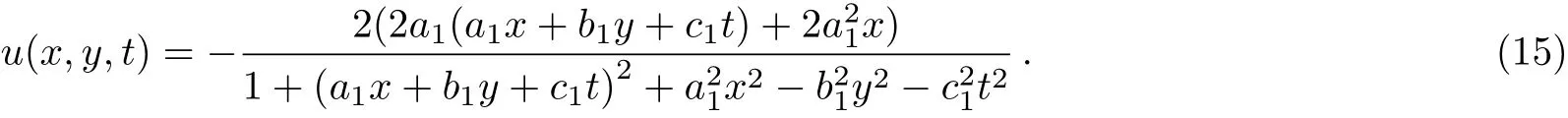
Observing the following Fig.2,we see that the shape of soliton is one convex wave upward and one concave wave downward,which are located in both sides of horizontal plane,so this soliton is described as the rational breather soliton.Further observation on the solution(15)and Fig.2,we will also find useful properties that it is not exponentially decaying but algebraically decaying.Furthermore,whenx(ory,t)→∞,u(x,y,t)→0.
Fig.2 The rationalbreathersoliton u(x,t) =?8x/(1+2x2+2t2)as y=t,a1=1,b1=i,c1=?i.
In addition,in Fig.2,we can also see the similar structure of the rogue wave which is localized in bothx-andt-directions.Thus,it shows that the solution(15)is the 2D rogue wave of(2+1)-dimensional PBLMP equation.
4 Spatio-Temporal Deformation of Kink-Breather
In the part,we will discuss spatio-temporal deformation of kink-breather for the(2+1)-dimensional PBLMP equation,and observe the process of solitons’interaction.So we will select the test function of the following form
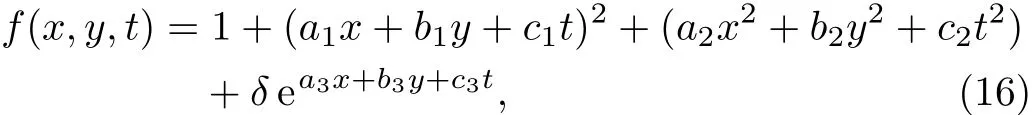
wheref(x,y,t)comprises a rational function and an exponential function,andai,bi,ci(i=1,2,3),δwill be determined later.Putting Eq.(16)in Eq.(6)by means of Maple,we obtain the following algebraic equations.
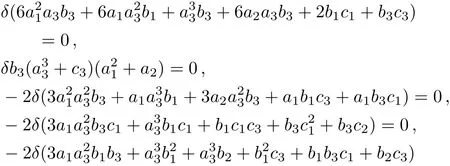
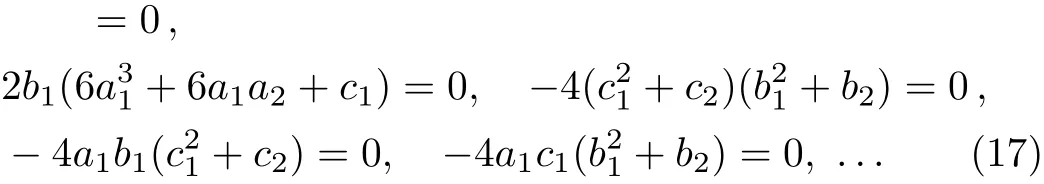
Solving Eqs.(17)we gain relations as follows
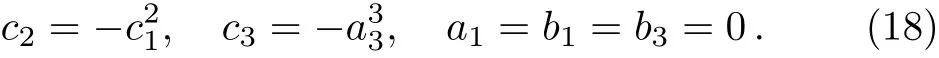
Plugging Eqs.(18)and(16)into(5),we can achieve new exact solitary wave solution of the(2+1)-dimensional PBLMP equation

wherea2,a3,b2andδare free.Pay attention to the solution(19),ifa3<0,the solutionu→?2a3ast→+∞,and the solutionu→ 0 ast→ ?∞. Conversely,ifa3>0,the solutionu→ 0 ast→ +∞,and the solutionu→ ?2a3ast→ ?∞.These asymptotic characteristics show that the solution(19)is the kink solitary wave solution.With further analysis of the solution(19),we notice that it is also the rational solution withx,y,so the solution(19)is the rational kink solitary wave solution.Therefore,the solution(19)is exponentially decaying and also algebraically decaying.It is the mixed exponential-algebraic solitary wave solution,[20]which has complex nature structure.Then critical parametersδ,a3will be analyzed about this complexity.In order to ensure the non-singularity of the solution(19),we assumeδ>0.
Whenδ>0,a3<0,we observe the following Fig.3 which shows the interaction process between the kink solitary wave and the rational breather soliton.It is found that the rational breather soliton will be drowned by the kink solitary wave finally,that is,a soliton fusion take place.
From Fig.3,we see that the rational breather soliton and the kink solitary wave are to interaction and annihilate step by step.
Whenδ>0,a3>0,we observe the following Fig.4,which is quite different from Fig.3. It is found that the kink solitary wave will degenerate into the rational breather soliton.
From Fig.4,we see that there is only the kink solitary wave at first.As time goes by,the rational breather soliton split offfrom the kink solitary wave.But at last,there is nothing except the rational breather soliton because of the kink solitary wave’s energy decay in the process of evolution over time.The kink solitary wave has become vestigial.The total energy is conserved,so the rational breather soliton absorb energy and exist.
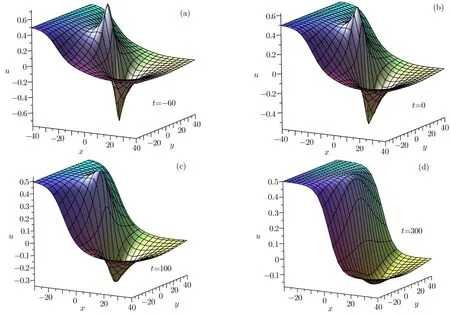
Fig.3 Spatial structure of the solution(19)at different time as a2=1,b2=1/2,a3= ?1/4,δ=16.
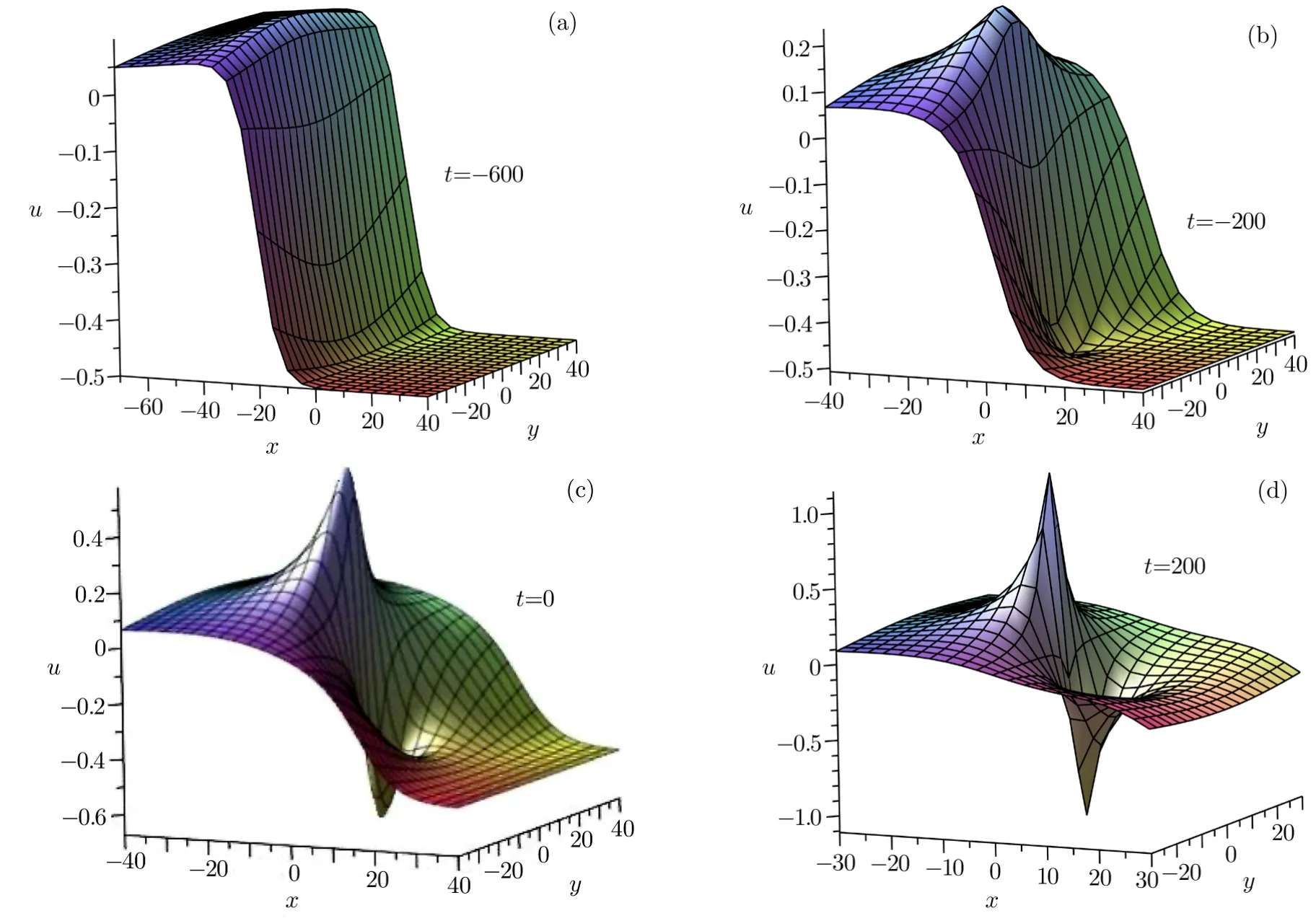
Fig.4 Spatial structure of the solution(19)at different time as a2=1,b2=1/2,a3=1/4,δ=16.
The above phenomena are necessary to study soliton dynamical complexity in the higher dimensional systems.Then,we put the focus on conditions about fusion and degeneration of soliton.At the same time,fusion and degeneration of soliton also illustrate that the solution(19)is not stable.
The solution(19)contains rational function and exponential function.Ifδ>0,a3<0,whent→ ?∞,the solution(19)stands for the rational breather soliton and the kink solitary wave.Whilet→+∞,exponential function rises faster than rational function so that the rational breather soliton is annihilated by the kink solitary wave,and the fusion of the solitary wave take place.Ifδ>0,a3>0,whent→ ?∞,the solution(19)represents the kink solitary wave solution.While in the vicinity oft=0,the kink solitary wave starts to become weak,and the rational breather soliton begins to become strong.The kink solitary wave and the rational breather soliton keep pace with each other.Whent→ +∞,exponential function goes to zero,so the kink solitary wave degenerates except for the rational breather soliton.
In addition,please note that the velocity of the kink solitary wave and the rational breather soliton in the solution(19)areandvr=0 on thex-axis.Thus we get the relation Δ(vr,vk)of betweenvrandvk:
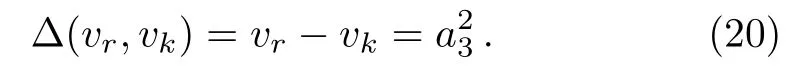
If Δ(vr,vk)=0,thenvr≡vk.At this time,a3=0,and you will find that there is no interaction of the solitary wave.They will remain the same speed along the way forward,and not affect each other.
If Δ(vr,vk)>0,thenvr>vk.Whena3<0,the solution(19)will be divided into the kink solitary wave and the rational breather soliton ast→ ?∞,but the solitary wave’s fusion will happen until only the kink solitary wave is left ast→+∞.Whena3>0,the solution(19)represents the kink solitary wave ast→ ?∞,but the kink solitary wave will degenerate into the rational breather soliton ast→ +∞.In the above process,the fusion and degeneration of the kink solitary wave occur.This also shows that the mixed algebraic-exponential solitary wave solution is unstable,and this type of solution contains rich dynamical properties of(2+1)-dimensional PBLMP equation.
5 Conclusion
In the paper,the kink solitary wave solution,the rational breather soliton and the kink-breather solitary wave are gained for the(2+1)-dimensional PBLMP equation by applying the Hirota bilinear method and selecting different test functions. Then we study spatio-temporal deformation of the kink solitary wave and the rational breather soliton,and find that the fusion and degeneration of the kink solitary wave occur in the process of evolution over time from theoretical analysis and figure display.It is found that the mixed exponential-algebraic solution is very useful in researching the soliton dynamical complexity in the higher dimensional systems.In the future,we will keep on trying to construct various types of exact solutions to discover more dynamical properties of the(2+1)-dimensional PBLMP equation.
[1]K.Kimiaki and W.Miki,Prog.Theor.Phys.53(1975)1652.
[2]C.H.Gu,H.S.Hu,and Z.X.Zhou,Darboux Transformation in Soliton Theory and Its Geometric Applications,Shanghai Science and Technology Press,Shanghai(2005).
[3]A.K.Pogrebkov,Theor.Math.Phys.181(2014)1585.
[4]R.Hirota and J.Satsuma,Phys.Lett.A 85(1981)407.
[5]H.W.Tam,W.X.Ma,X.B.Hu,and D.L.Wang,J.Phys.Soc.Jpn.69(2000)45.
[6]X.B.Hu,J.Phys.A:Math.Gen.30(1998)8225.
[7]G.Z.Tu,Sci.China(Serries A)32(1989)142.
[8]M.Jimbo and T.Miwa,Publications of the Research Institude for Mathematical Sciences Kyato University 19(1983)943.
[9]Z.H.Zhao and Z.D.Dai,Int.J.Nonl.Sci.Numer.Simulation 11(2010)679.
[10]X.Zhao,L.Wang,and W.Sun,Chaos,Solitons and Fractals 28(2006)448.
[11]M.Senthilvelan,Appl.Math.Comp.123(2001)381.
[12]J.H.He,Phys.Lett.A 335(2005)182.
[13]A.V.Mikhailov.Phys.D 3(1981)73.
[14]M.J.Ablowitz and P.A.Clarkson,Solitons,Nonlinear Evolution Equations and Inverse Scattering,Cambridge University Press,Cambridge(1991).
[15]V.O.Vakhnenko,E.J.Parkes,and A.J.Morrison,Chaos,Solitons and Fractals 17(2003)683.
[16]B.Ren,J.Yu,and X.Z.Liu,Commun.Theor.Phys.65(2016)341.
[17]L.Wang,S.F.Tian,Z.T.Zhao,and X.Q.Song,Commun.Theor.Phys.66(2016)35.
[18]D.S.Wang,X.G.Li,C.K.Chan,and J.Zhou,Commun.Theor.Phys.65(2016)259.
[19]C.J.Wang,Z.D.Dai,and C.F.Liu,Mediter.J.Math.(2015)1.
[20]W.Tan and Z.D.Dai,Nonlinear Dyn.85(2016)817.
[21]X.Y.Tang,Phys.Lett.A 314(2003)286.
[22]F.Z.Lin and S.H.Ma,Adv.Mater.Res.912–914(2014)1303.
[23]C.Tian,The Lie Group and Its Applications in Differential Equation,Science Press,Beijing(2001).
[24]Y.Li and D.Li,Appl.Math.Sci.6(2012)579.
[25]N.Liu and X.Q.Liu,Chin.J.Quant.Electr.25(2008)546.
[26]Y.N.Tang and W.J.Zai,Nonlinear Dyn.81(2015)249.
 Communications in Theoretical Physics2017年5期
Communications in Theoretical Physics2017年5期
- Communications in Theoretical Physics的其它文章
- Anharmonic Properties of Aluminum from Direct Free Energy Interpolation Method?
- Effects of Interfaces on Dynamics in Micro-Fluidic Devices:Slip-Boundaries’Impact on Rotation Characteristics of Polar Liquid Film Motors?
- Controlling Thermodynamic Properties of Ferromagnetic Group-IV Graphene-Like Nanosheets by Dilute Charged Impurity
- Elastic Deformation Analysis on MHD Viscous Dissipative Flow of Viscoelastic Fluid:An Exact Approach
- Entropy Generation Analysis in Convective Ferromagnetic Nano Blood Flow Through a Composite Stenosed Arteries with Permeable Wall
- Isotopic Effects on Stereodynamics of the C++H2→ CH++H Reaction?
