Entropy Generation Analysis in Convective Ferromagnetic Nano Blood Flow Through a Composite Stenosed Arteries with Permeable Wall
Noreen Sher Akbarand Adil Wahid Butt,?DBS&H,CEME,National University of Sciences and Technology,Islamabad,Pakistan DBS&H,MCE,National University of Sciences and Technology,Islamabad,Pakistan
1 Introduction
Blood flow is a continuous process of the circulation in the cardiovascular system.This process of flow also carries out the transportation of nutrients,hormones,metabolic wastes,O2and CO2,the temperature of whole body,the regulation of the pH and the protection from mechanical and microbial harms.[1]This complete science which describes the physics of blood flow is known as hemodynamics.For general understanding,one should be familiar with the anatomy of the cardiovascular system and hydrodynamics.However,it is pertinent to mention that blood is not a Newtonian fluid,and blood vessels are not just any rigid tubes,therefore the classic hydrodynamics is not sufficient enough for the explanation of this hemodynamics.[2]Chakravarty and Mandal[3]modelled and mathematical studied the blood flow through an overlapping arterial stenosis.They examined the characteristics of unsteady blood flow in an artery with a time dependent stenosis using the power-law fluid model.In another article,Chakravarty and Mandal[4]discussed a theoretical study on the nonlinear behaviour of blood flow over a single cardiac cycle through an arterial segment having an overlapping stenosis when it is subjected to whole body acceleration.They yield an estimate of the effects of the body acceleration,the pressure gradient,the vessel wall deformability and the severity of the stenosis on the unsteady flow characteristics of blood.Mishra and Chakravarty[5]studied flow in arteries in the presence of stenosis.In their article,the effect of the surrounding connective tissues on the motion of the wall has been incorporated.Recent literature on the topic can be viewed through Refs.[6–13].
Nano fluids are a sort of new group of fluids which consist of a base fluid with nano-sized particles(1 nm–100 nm)balanced with in them.Nano fluid was anticipated by Choi[14]at Argonne National Laboratory in 1995.Through his analysis of nano fluids,he studied the condensed pumping supremacy as compared to pure liquor to attain corresponding heat transfer strengthening and particle clogging.Xuan and Roetzel[15]carried the investigation of a nano fluid flow within a tube using a diffusion model.The enrichment of heat transfer of nano fluids in a two-dimensional enclosed space is elaborated by Khanafer et al.[16]for all concerned physical constraints.They used the model to examine heat transfer analysis of nano fluids contained by an enclosure taking into consideration of the solid constituent part of dispersion.Appraisal of convective heat transfer augmentation with nano fluids is given by Kaka?c and Pramuanjaroenkij.[17]In the peristaltic prose,nano fluid was first discussed by Nadeem and Akbar.[18]They discussed endoscopic effects on the peristaltic flow of a nano fluid.They made the analysis in two concentric tubes and discussed the applications of endoscope.Nano fluids are basically fluids with very very small size of nanoparticles,in blood these particles are inserted in blood diagnosing diseses like cancer theses nanoparticles are further useful in angiography,angioplasity etc.So nano fluids are quite useful in biomedical engineering highly connected with blood.Ellahi et al.[19]studied the blood flow of nano fluid through an artery with composite stenosis and permeable walls.They studied the velocity distribution along with impedance variation,the variation of concentration and temperature distribution,shear stress and trapping phenomenon of blood flow of nano fluids in human arteries.Recent articles on the nano fluids are cited in Refs.[19-23].
The study of entropy is the measure of the unavailable energy in a closed thermodynamic system,which isusually considered to be a measure of the system’s disorder.It is a property of the state of system which directly changes with any reversible change in heat in the system and inversely with the temperature.Bejan[24]studied the entropy generation analysis with fundamental convective heat transfer.Entropy generation in a pipe due to non-Newtonian fluid flow for constant viscosity case have been discussed by Pakdemirli and Yilbas.[25]In this regard,Nada[26]gave the idea of entropy generation due to heat and fluid flow in backward facing step flow with various expansion ratios.Oztop et al.[27]presented entropy generation through hexagonal cross-sectional duct for constant wall temperature in laminar flow.Further literature on entropy generation can be viewed through Refs.[28–38].
The recent advancements in the field of nano fluids has caught the interest of many scientists across the world to study phenomenon of peristalsis with nano fluids.However,according to the authors knowledge,the blood flow with entropy generation analysis has not been explored so far.To fill this gap,we here present the study of entropy generation analysis of the blood flow in the arteries with permeable walls.The convection through the flow is studied with compliments to the entropy generation.Governing problem is formulized and solved for low Reynold’s number and long wavelength.Exact analytical solutions have been obtained and are analyzed graphically.It is seen that temperature for pure water is lower as compared to the copper water.It gains magnitude with an increase in the slip parameters.
2 Formulation of the Problem
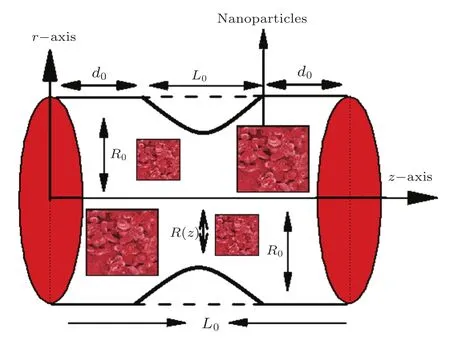
Fig.1 Geometry of the problem.
Let us consider a circular tube of finite lengthLand permeable walls as shown in Fig.1.The axisymmetric flow of blood through the arterial wall with composite stenosis is described by Srivastava et al.[8]as:
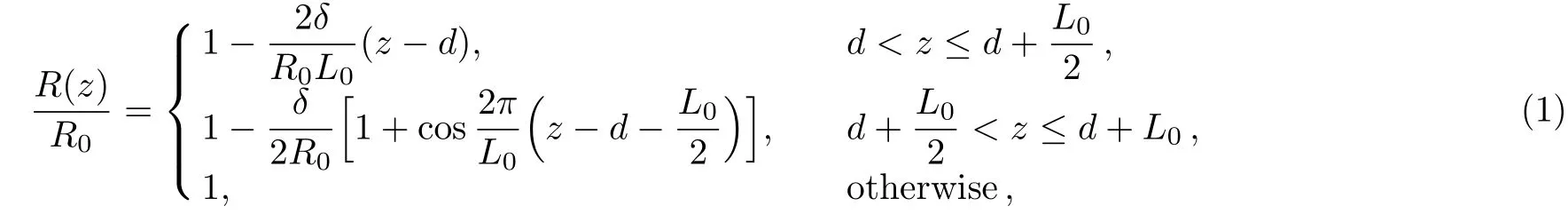
whereR0,R(z),L0,d,δare the radius of normal artery,radius of the artery in the obstructed region,the length,location and height of the stenosis respectively.The governing equations for an incompressible nano fluid can be written as
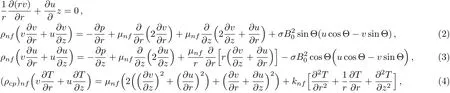
with the conditions:
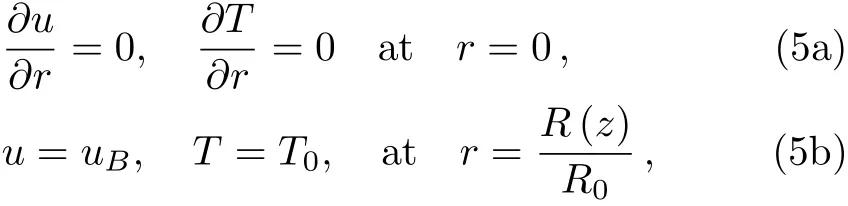
whererandzare the coordinates.zis taken as the center line of the tube andrtransverse to it,uBslip velocity,uandvare the velocity components in therandzdirections respectively,Tis the local temperature of the fluid.Further,ρnfis the effective density,μnfis the effective dynamic viscosity,(ρcp)nfis the heat capacitance,αnfis the effective thermal diffusivity,andknfis the effective thermal conductivity of the nano fluid,which are defined as in Ref.[10].
We introduce the following non-dimensional variables:
whereUis the velocity averaged over the section of the tube with radiusR0.Making use of these variables in Eqs.(2)–(5)and applying the additional condition of long wavelength and low Reynold’s number(δ/R0? 1;?=R0/L0=o(1))for the case of mild stenosis,the nondimensional governing equations after dropping the dashes can be written as:
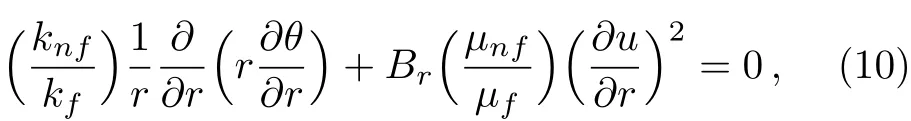
whereM,βandGrare the Hartmann number,heat absorption parameter,and Grashof number respectively.The non-dimensional boundary conditions on velocity and temperature for permeable wall are:
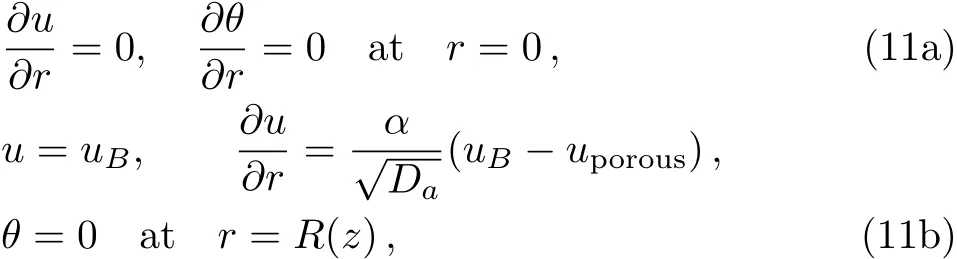
whereuBis the slip velocity yet to be determined,Dais Darcy number anduporousis given asuporous=?Da(dp/dz)and
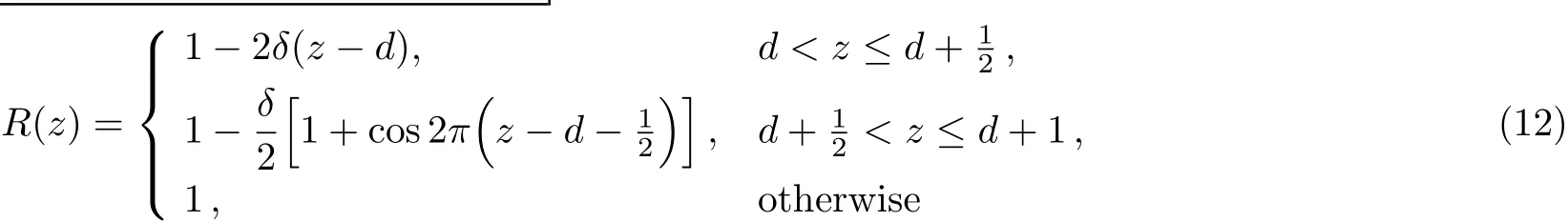
3 Viscous Dissipation and Entropy Generation Analysis
The dimensional viscous dissipation termˉΦ can be obtained from equations of motion,i.e.[24?34]
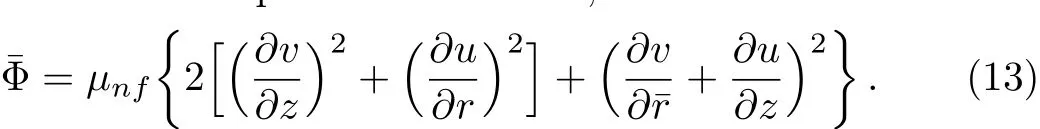
The dimensional volumetric entropy generation is defined as[24?34]
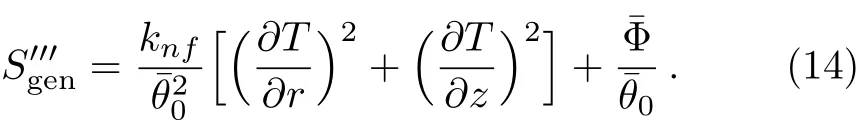
Dimensionless form of the Entropy Generation is given as:
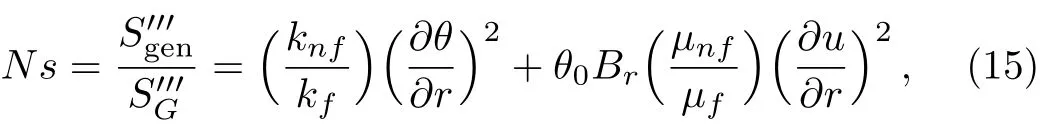
where
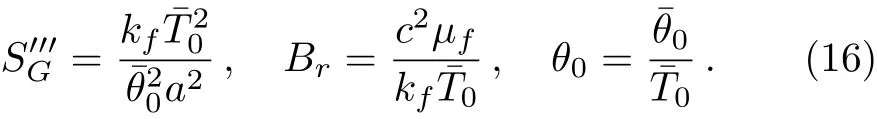
Equation(15)consists of two parts.The first part is the entropy generation due to finite temperature difference(Nscond)and the second part is the entropy generation due to viscous effects(Nscond).The Bejan number is defined as[24?34]
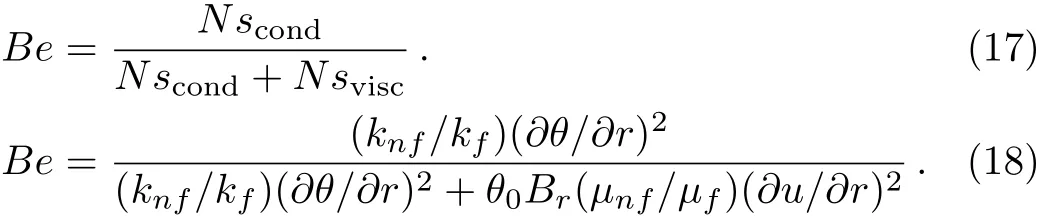
4 Exact Solutions
Solving Eqs.(9),(10)together with boundary conditions,we obtain the analytical solution of velocity profile as follows:

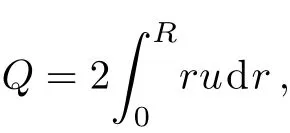
which implies:
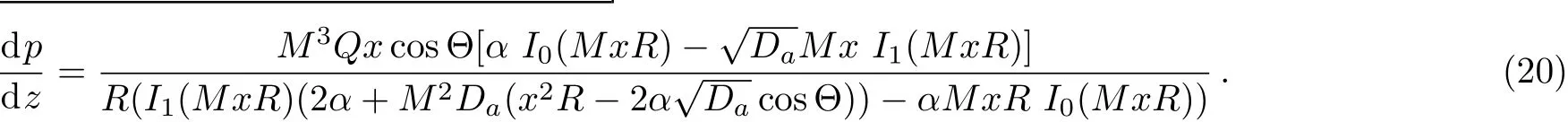
Substituting Eq.(19)in Eq.(10)and solving for the temperature profileθ,we obtain:
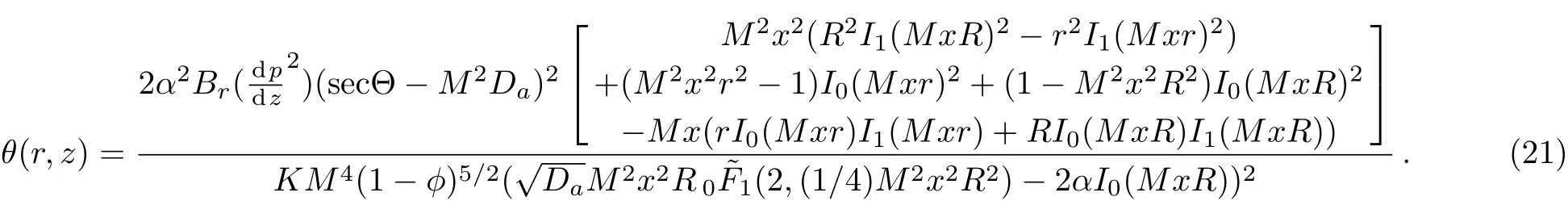
Impedance resistanceλis calculated as:
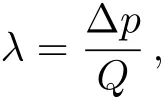
since the flow rateQis a constant for all sections of tube
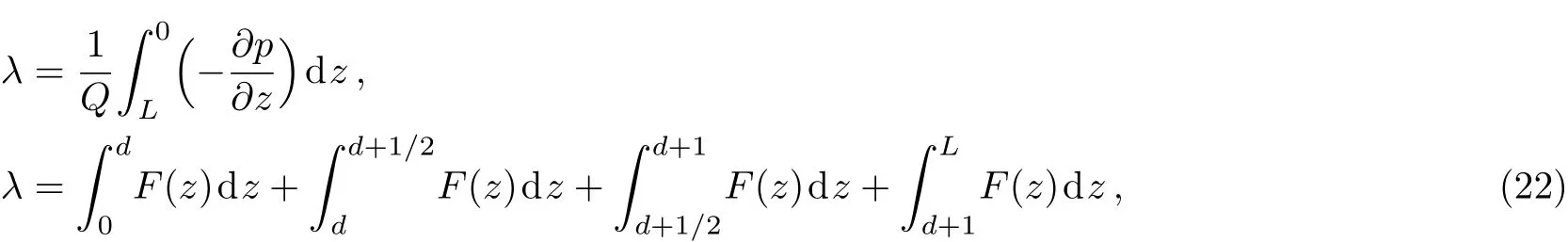
where

5 Results and Discussion
In this section,we have graphically discussed the exact solutions obtained in the previous section.The graphical results are represented with physical interpretation.The velocity profileu(r,z)is plotted against the radial axisrfor different values of the slip parameterα,Hartmann numberM, flow rateQand Darcy numberDain Figs.2(a)–2(d).It is observed that the velocity is symmetric for all the parameters and is maximum at the walls but minimum at the center of the tube.Velocity increases with an increase in Hartmann number,the flow rate,and Darcy number,whereas it decreases for higher values of the slip parameter.Also we note that the magnitude of velocity falls down as we increase the amount of copper in the base fluid.
The distribution of temperature around the tube is shown in Figs.3(a)–3(c)Temperature as it stands attains its peak values at the center of the tube and lower temperature is seen as we move towards the boundaries of the tube.We note that the addition of copper nanoparticles in the base fluid increases the heat transfer along the tube.Temperature for pure water is lower as compared to the copper water.It gains magnitude with an increase in the slip parameter and an opposite behaviour is seen for an increment Hartmann number and Darcy number.
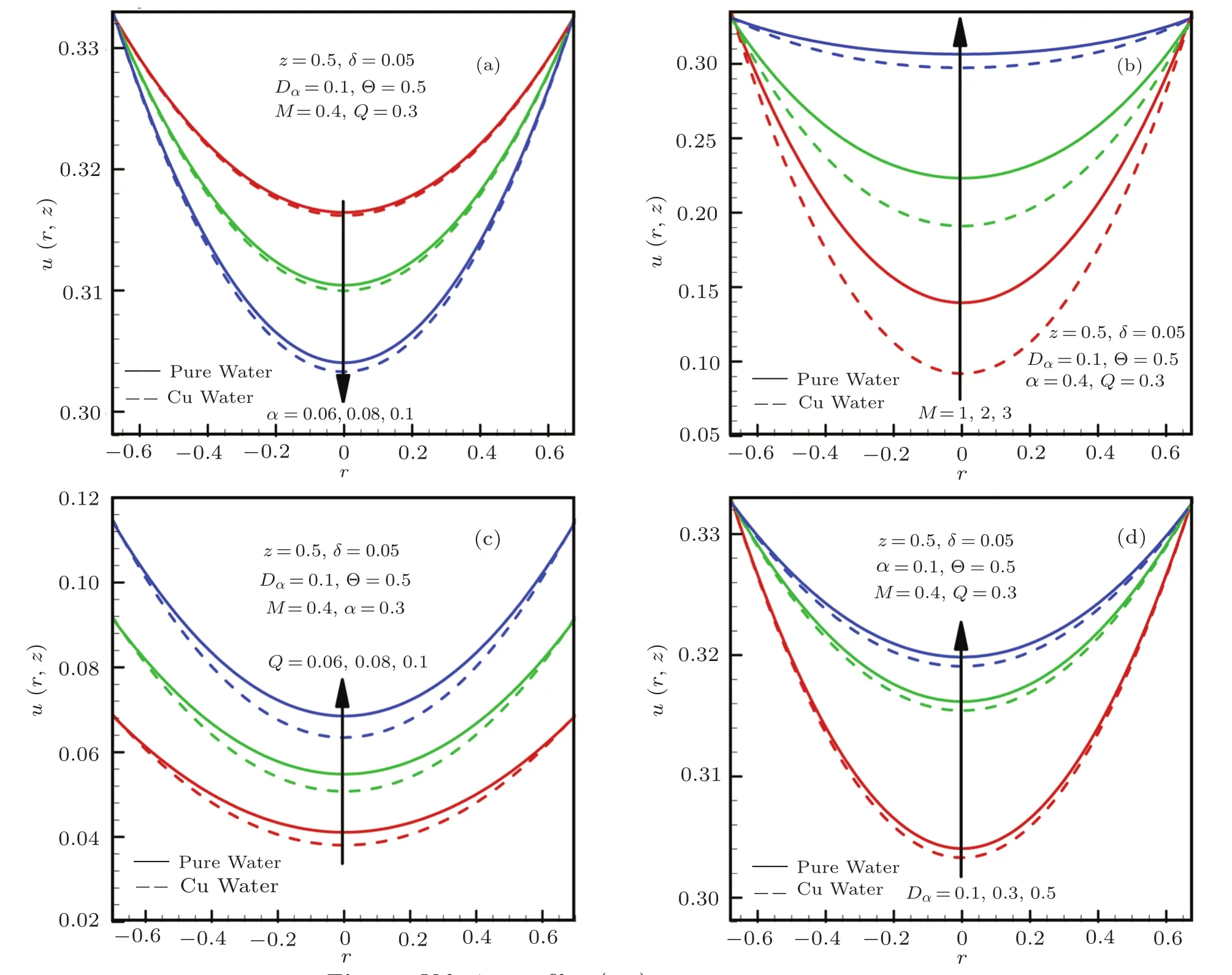
Fig.2 Velocity profile u(r,z).
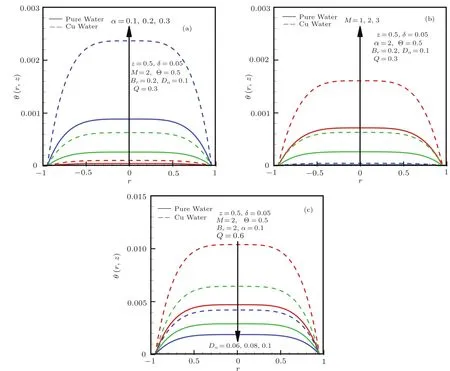
Fig.3 Temperature profile θ(r,z).
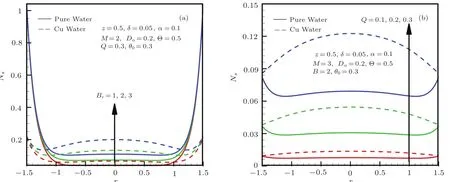
Fig.4 Entropy generation number Ns(r,z).
The entropy generation around the tube is shown in Figs.4(a)–4(b)Entropy generally has a non-uniform behaviour but its generation is rapid for cu-water in comparison to the pure water.Pressure gradient rises with an increase in the slip parameter as shown in Fig.5(a).Graphical representation depicts that when the viscous forces are lower than the electromagnetic forces,i.e.Hartmann number increases,pressure gradient decreases significantly.In both cases,pressure gradient remains greater when copper is added to the base fluid.
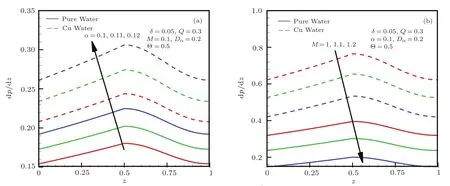
Fig.5 Pressure gradient dp/dz.
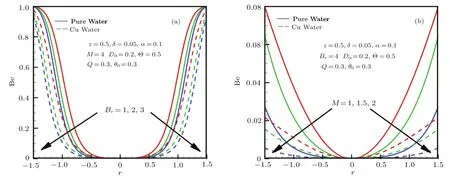
Fig.6 Bejan number Be.
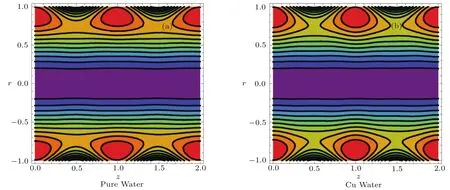
Fig.7 Streamlines.
Figures 6(a)–6(b)are prepared to see the variation of Bejan number with respect to change in different physical constraints.The pictorial representation shows a beautiful variation for Bejan number when we increase the Brinkman number and the Hartmann number.In both cases the Bejan number decreases,however more rapidly in case of the later.Bejan number is least near the center of the tube and maximum near the walls.For cu-water,it attains comparatively smaller value than that of pure water.
Figures 7(a)–7(b)depict streamlines for pure and copper water.Size of the trapped bolus for pure water is greater when compare to copper water.But number of trapped bolus for copper water are greater when compare to the pure water.
6 Conclusion
Entropy generation analysis in the convective ferromagnetic nano blood flow through a composite stenosed arteries with permeable wall is studied.Key points of the performed analysis are as follows
In this section,we have graphically discussed the exact solutions obtained in the previous section.
(i)It is observed that the velocity is symmetric for all the parameters and is maximum at the walls but minimum at the center of the tube.
(ii)Velocity increases with an increase in Hartmann number,the flow rate and Dawhereas it decreases for higher values of the slip parameter.
(iii)Temperature for pure water is lower as compared to the copper water.It gains magnitude with an increase in the slip parameter and the Hartmann number and an opposite behaviour is seen for an increment in Da.
(iv)In both cases,pressure gradient remains greater when copper is added to the base fluid.
(v)Bejan number is least near the center of the tube and maximum near the walls.For cu-water,it attains comparatively smaller value than that of pure water.
(vi)Size of the trapped bolus for pure water is greater when compared to copper water.But number of trapped bolus for copper water are greater when compared to the pure water.
[1]J.G.Tortora and B.Derrickson,The Cardiovascular System:The Blood.Principles of Anatomy&Physiology,13th.John Wiley&Sons,Inc,Mark Nielson,Shawn D.Miller(2012)729.
[2]J.Joel,S.Fieldman,D.H.Phong,Y.Saint-Aubin,and L.Vinet,Rheology.Biology and Mechanics of Blood Flows,Part II:Mechanics and Medical Aspects,Springer-Verlag,New York(2007)119.
[3]S.Chakravarty and P.K.Mandal,Math.Comp.Model 19(1994)59.
[4]S.Chakravarty and P.K.Mandal,Math.Comp.Model 24(1996)43.
[5]J.C.Mishra and S.Chakravarty,J.Biomech.19(1986)907.
[6]D.Tripathi,J.Bio.Eng.9(2012)119.
[7]S.Mishra,S.U.Siddiqui,and A.Medhavi,Int.J.Appl.Math.6(2011)58.
[8]V.P.Srivastava,Vishnovi,and Rochana,J.Sci.Tech.5(2010)55.
[9]N.S.Akbar,Int.J.Biomath 7(2014)1450004.
[10]N.S.Akbar and A.W.Butt,J.Magn.Matter 381(2015)285.
[11]R.Ellahi,S.U.Rahman,and S.Nadeem,Zeitschrift Fur Naturforschung A 68a(2013)489.
[12]R.Ellahi,S.U.Rahman,S.Nadeem,and K.Vafai,J.Appl.Math.Inf.Sci.8(2014)1.
[13]R.Ellahi,S.U.Rahman,S.Nadeem,and N.S.Akber,J.Comput.Theor.Nanosci.11(2014)1.
[14]S.U.S.Choi,Enhancing Thermal Conductivity of Fluids with Nanoparticles,in:Developments and Applications of Non-Newtonian Flows,Vol.66,eds.D.A.Siginer and H.P.Wang,ASME,New York(1995)99.
[15]Y.Xuan and W.Roetzel,Int.J.Heat Mass Transf.43(2000)3701.
[16]K.Khanafer,K.Vafai,and M.Lightstone,Int.J.Heat Mass Transf.46(2003)3639.
[17]K.Sadik and A.Pramuanjaroenkij,Int.J.Heat Mass Transf.52(2009)3187.
[18]N.S.Akbar and S.Nadeem,Commun.Theor.Phys.56(2011)761.
[19]R.Ellahi,S.U.Rahman,S.Nadeem,and N.S.Akbar,Appl.Nanosci.4(2014)919.
[20]M.Sheikholeslami,M.G.Bandpy,R.Ellahi,M.Hassan,and S.Soleimani,J.Magn.Matter 349(2014)188.
[21]M.Sheikholeslami,D.D.Ganji,M.Y.Javed,and R.Ellahi,J.Magn.Matter 374(2015)36.
[22]W.Ibrahim and O.D.Makinde,Comput.Fluids 86(2013)433.
[23]W.Ibrahim and O.D.Makinde,J.Nano fluids 4(2015)1.
[24]A.Bejan,J.Heat Transf.101(1979)718.
[25]M.Pakdemirli and B.S.Yilbas,Indian Academy of Science,Sadhana 31(2006)21.
[26]E.Abu-Nada,Int.J.Energy 3(2006)419.
[27]H.F.Oztop,A.Z.Sahin,and I.Dagtekin,Int.J.Energy Res.28(2004)725.
[28]I.Dagtekin,H.F.Oztop,and A.Z.Sahin,Int.J.Heat Mass Transf.48(2005)171.
[29]T.Basak,R.Anandalakshmi,P.Kumar,and S.Roy,Energy 37(2012)514.
[30]I.Dagtekin,H.F.Oztop,and A.Bahloul,Int.Commun.Heat Mass 34(2007)502.
[31]H.F.Oztop and K.Al-Salem,Ren.Sust.En.Reviews 16(2012)911.
[32]R.Ellahi,M.Hassan,and A.Zeeshan,Int.J.Heat Mass Transf 81(2015)449.
[33]N.S.Akbar,Entropy 17(2015)1411.
[34]R.Ellahi,Sha fiq Ur Rahman,S.Nadeem,and K.Vafai,Commun.Theor.Phys.63(2015)353.
[35]N.S.Akbar,Energy 82(2015)23.
[36]R.Ellahi,M.M.Bhatti,C.Fetecau,and K.Vafai,Commun.Theor.Phys.65(2016)66.
[37]N.S.Akbar,J.Bionic Eng.12(2015)656.
[38]N.S.Akbar,IEEE Trans.NanoBioscience 14(2015)780.
 Communications in Theoretical Physics2017年5期
Communications in Theoretical Physics2017年5期
- Communications in Theoretical Physics的其它文章
- Elastic Deformation Analysis on MHD Viscous Dissipative Flow of Viscoelastic Fluid:An Exact Approach
- Inverse Scattering Transform of the Coupled Sasa–Satsuma Equation by Riemann–Hilbert Approach?
- Magnetic Effect Versus Thermal Effect on Quark Matter with a Running Coupling at Finite Densities?
- Borromean Windows for Three-Particle Systems under Screened Coulomb Interactions?
- Isotopic Effects on Stereodynamics of the C++H2→ CH++H Reaction?
- Effects of Interfaces on Dynamics in Micro-Fluidic Devices:Slip-Boundaries’Impact on Rotation Characteristics of Polar Liquid Film Motors?
