Numerical simulation of three-dimensional breaking waves and its interaction with a vertical circular cylinder *
Zhihua Xie, Lin Lu (呂林), Thorsten Stoesser, Jian-guo Lin (林建國), Dimitrios Pavlidis,
Pablo Salinas3, Christopher C. Pain3, Omar K. Matar4
1. School of Engineering, Cardiff University, Cardiff, CF24 3AA, UK, E-mail: zxie@cardiff.ac.uk
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,Dalian 116023, China
3. Department of Earth Science and Engineering, Imperial College London, London, SW7 2AZ, UK
4. Department of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK
5. College of Environmental Science and Engineering, Dalian Maritime University, Dalian 116026, China
Numerical simulation of three-dimensional breaking waves and its interaction with a vertical circular cylinder*
Zhihua Xie1,2,3,4, Lin Lu (呂林)2, Thorsten Stoesser1, Jian-guo Lin (林建國)5, Dimitrios Pavlidis3,
Pablo Salinas3, Christopher C. Pain3, Omar K. Matar4
1. School of Engineering, Cardiff University, Cardiff, CF24 3AA, UK, E-mail: zxie@cardiff.ac.uk
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology,Dalian 116023, China
3. Department of Earth Science and Engineering, Imperial College London, London, SW7 2AZ, UK
4. Department of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK
5. College of Environmental Science and Engineering, Dalian Maritime University, Dalian 116026, China
Wave breaking plays an important role in wave-structure interaction. A novel control volume finite element method with adaptive unstructured meshes is employed here to study 3-D breaking waves. The numerical framework consists of a “volume of fluid” type method for the interface capturing and adaptive unstructured meshes to improve computational efficiency. The numerical model is validated against experimental measurements of breaking wave over a sloping beach and is then used to study the breaking wave impact on a vertical circular cylinder on a slope. Detailed complex interfacial structures during wave impact, such as plunging jet formation and splash-up are captured in the simulation, demonstrating the capability of the present method.
Breaking waves, volume of fluid method, 3-D simulation, Navier-Stokes equation, adaptive unstructured mesh
Introduction
Wave breaking plays an important role in marine hydrodynamics,wave-structureinteraction,air-sea interaction, surf zone dynamics, and nearshore sediment transport.Severalcomprehensivereviewsof breaking waves and wave mechanics can be found in Refs.[1-3].
Wave-structure interaction is a key aspect in the safe and cost-effective design of coastal and offshore structures, and marine renewable devices. In order to roughly predict the hydrodynamic loads on structures,the Morison equation and potential flow theory have been widely used in the literatures.However,it is challenge toconsider breaking wave impact on the structures by using these two approaches, especially when there are splash-up and air entrainment[4].
With developments of computational fluid dynamics (CFD) and increases in computer power, recent modelsfor studying free surfaceflows,including breaking waves,solve the Navier-Stokesequations coupled with a free surface calculation (see Lin[5]for comprehensivemodelling applicationsand methodologies for water waves and McSherry et al.[6]for large-eddy simulation of free surface flows). There are several numerical studies on breaking wavesin the literature based on one-phase flow model in 2-D[7-10]and 3-D[11,12], in which only the flow in the water is considered in the computations. The pressure in the air is taken as a constant, and the boundary conditions are approximately specified at the free surface. In order to take theeffect of air phaseintoaccount for wave breaking, several 2-D two-phase flow model, in which both flows in the air and water are solved, have been developed to study the details of breaking waves in thesurf zone[13,14],overturning jet during wave breaking[15]and the effect of wind on breaking waves[16,17]. Several 3-D two-phase flow models have alsobeen developed tounderstand 3-Dbreaking wavesin a periodicspacedomain[18],over a planebeach[19]and over a complex topography[20],which have provided much insight into the kinematics and dynamicsof breaking waves,including theoverturning jet and thesubsequent splash-upprocess.Previousinvestigationshavegreatly improved our knowledge of breaking waves, however, little attention has been given for the numerical study on the 3-D waveaction on a vertical circular cylinder over a slope.
In this study, a 3-D two-phase flow model with adaptive unstructured meshes is developed to investigate3-Dbreaking waveinteraction with a vertical circular cylinder along a constant sloping beach,which can provide detailed information on the impact forceduring wave breaking. The usageof adaptive unstructured meshes is helpful to reduce the computational efforts in CFD simulations and is also easy to deal with the problems with irregular boundaries. The description of the mathematicalmodel for the twophase flow is described in next section. The numerical method is presented after that. Both 2-D overturning waves and 3-D breaking wave impacting on a cylinder aresimulated in the resultsand discussion section.Detailed computationalresultsof thewater surface profilesassociated with theadaptiveunstructured meshes are shown and discussed. Finally, conclusions are drawn.
1. Mathmatical model
A multi-fluid modelling framework hasbeen developed based on the multi-component modelling approach with information on interfacesembedded into the continuity equations. In two-phase flows, let iα be the mass fraction of phase i, where=1,2i,the density and dynamic viscosity of phaseiareiρ andiμ, respectively. A constraint on the system is

For each fluid component i, the conservation of mass may be denoted as
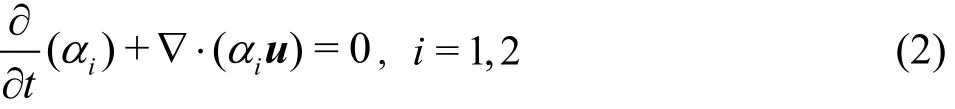
and the equations of motion of an incompressible fluid can be written as

wheretis the time,uis velocity vector,pis the pressure,thebulk density isρ = ρ1α1+ ρ2α2,the bulk dynamicviscosity is μ = μ1α1+ μ2α2, is thegravitational acceleration vector,isthe surfacetension coefficient,κ=▽·n isthe interfacial curvature,nis the interface unit normal,and δis the Dirac delta function.
2. Numerical method
In the present study, a transient, mixed, controlvolume and finite-element formulation isused to discretise the governing equations (Eq.(2) and Eq.(3)).A finitevolumediscretisation of thecontinuity equations and a linear discontinuous Galerkin (DG)[21]discretisation of the momentum equationsare employed with backward Euler time stepping. Within each time-step, the equations are iterated upon using a projection-based pressure determination method until all equations are simultaneously balanced. The main numerical framework includesa finite element type P1DG-P2(linear discontinuousvelocity between elements and quadratic continuous pressure between elements)for multi-fluid flow problems,which ensuresexact balancebetween buoyancy forceand pressure gradient.Theframework alsofeaturesa novel interfacecapturingscheme based on compressive control volume advection method[21], involving a high-order accuratefinite element method toobtain fluxes on the control volume boundaries, where these fluxes are subject to flux-limiting using a normalised variablediagram approach toobtain bounded and compressive solutionsfor theinterface.The implementation of capillary/surfacetension forcein the framework using an unstructured mesh minimises spurious velocities often found in interfacial flows[22].Finally,useof anisotropicunstructured mesh adaptivity[23]allowsthe grid resolution tobe concentrated in relatively important regions, such as the vicinity of interfaces, while lower resolution can be used in other regions; this leads to a significant gain in computationalefficiency without sacrificing accuracy.
The numerical framework has been validated and employed tostudy variousmultiphaseflow problems[24-27].Thedetailed modelling of three-dimensional bubbles, droplet and liquid films can be found in Xie et al.[22,28].
3. Results and discussion
3.1 2-D breaking wave over a sloping beach
In thissection,wesimulatea 2-Doverturning solitary wave and compare quantitatively with the experiment[29]for a breaking solitary wave splash-up on a 1:15sloping beach.Wefollowed thesame computational setupin our previousstudieswith a two-phase flow solver based on the finite volume method on a fixed grid[15,20]. At the inlet, the solitary wave is generated by giving the water surface profile and the water particle velocities[15], whereas the noslip wall boundary condition is applied at the sloping beach and zero-gradient boundary conditionsare applied at thetopand outlet of the computational domain.
Figure 1 shows the evolution of zoom in region for the solitary wave before and after wave breaking.It can be seen that the development of plunging jet, jet impingement and generation of splash-up are reproduced in the simulation. Sharp air-water interface is captured by the adaptive unstructured mesh, with fine mesh in the vicinity of the interface and coarse mesh away from the interface. A detailed comparison of the plunging jet, at the time of wave overturning, between the simulation and experimental results isshown in Fig.2. Good agreement is obtained in the present study in terms of wave shape and breaking location, demonstrating the capability of the present method in simulation wave breaking problems.
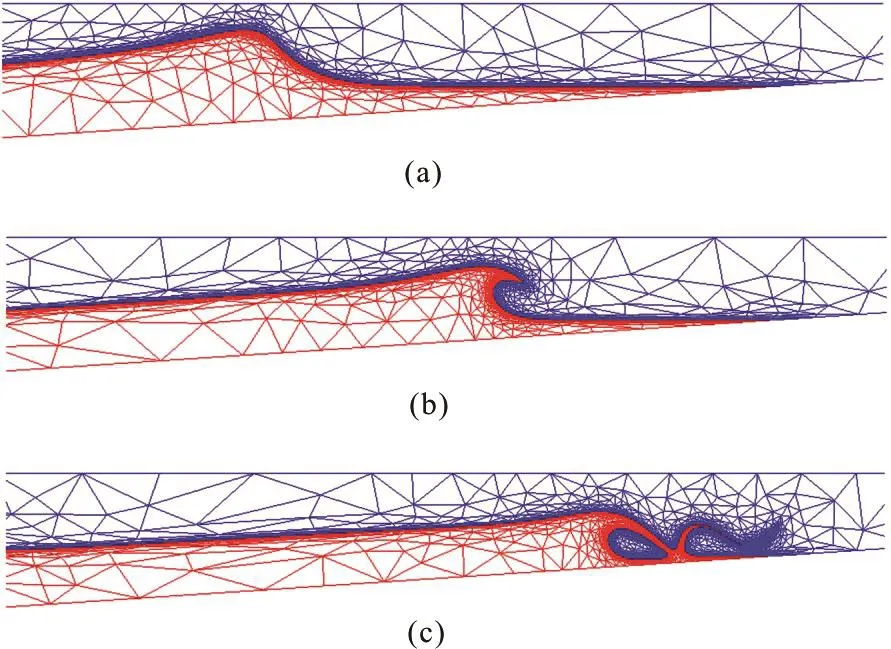
Fig.1 (Color online) Evolution of a solitary breaking wave with H / D = 0 .45along a 1: 1 5 sloping bea ch. W ater and air andtheirassociatedfullyunstructuredmeshareshown in red and blue colors
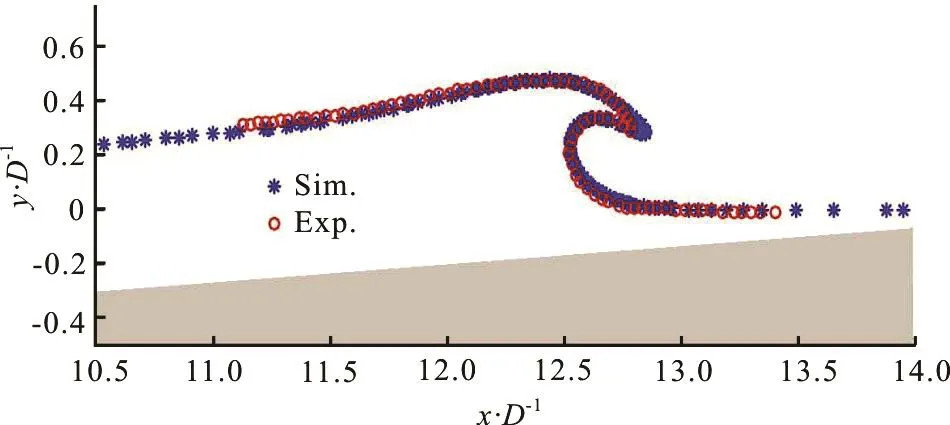
Fig.2 (Color online) Comparison between simulation and experimental measurements[29]for the wave surface profile during wave overturning on a sloping beach
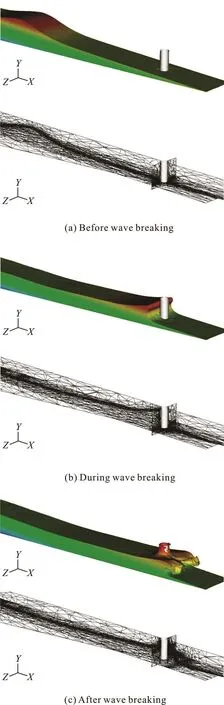
Fig.3 (Color online) Detailed views of the water wave surface.Top pannel shows the water surfaces colored based on local values of /yDand bottom pannel shows the fully-unstructured mesh corresponded to the top pannel along three slices
3.23-D Breaking wave impact on a vertical circular cylinder
A 3-Dsolitary breaking waveover a constant slopeisinvestigated here.In thecomputation,the origin of the coordinates is located at the still water levelin thecentre of the toeof theslopeand all lengthsarenormalized by thewater depth D=0.3048m . The computational setup is similar to the case for a 3-D breaking wave without a cylinder[20],in which theslope is1:15and theincident plane solitary wave with the ratio of wave height to water depth is H / D = 0.45.A verticalcircular cylinder with a diameter of d /D = 0.33is considered here and it is located at a distance of =12.5x D from the toeof theslope.Thecomputationaldomain, which has a length of 19.75D, width of 1.3D, and height of 1.75D, is discretized by an adaptive fully-unstruc-thestreamwise,verticaland spanwisedirections,respectively.
Figure 3 shows snapshots of detailed views of the solitary wave before, during and after wave breaking.Before wave breaking, it can be seen that the wave crest becomessteepdue totheshoaling effect(Fig.3(a)). A typical three-dimensional overturning jet just ahead of thecylinder can beseen in Fig.3(b)during wavebreaking.Thebreaking waveimpacts with the vertical cylinder and 3-D complex plunging jet isdeveloped in Fig.3(c).Theadaptivefullyunstructured meshes are also shown in Fig.3 and it can be seen that fine mesh is used in the vicinity of the interfaceand theregion near thecylinder whereas coarse mesh is used away from the interface. This has the advantage of reducing computational effort without sacrificing accuracy.
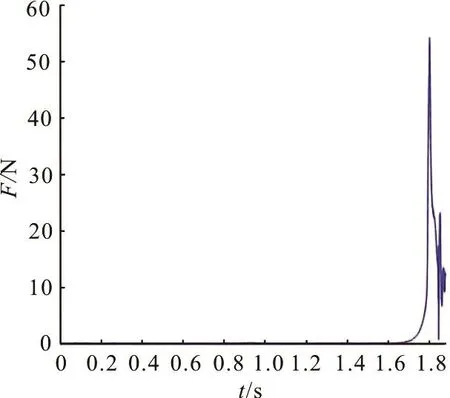
Fig.4 (Color online) Streamwise impact force on the vertical circular cylinder for the breaking wave along the sloping beach
Figure 4showsthe streamwise-component impact forceon the vertical cylinder during wave propagation along thesloping beach. It can be seen that the force is very small when the wave is far away from the cylinder. It gradually increases and obtains themaximum value when the plunging jet hits the cylinder. Then impact force gradually decreases when thebreaking wave passesby and there issome oscillation duetothree-dimensionaleffect of the breaking waves.
4. Conclusions
In thispaper,a controlvolumefiniteelement method with adaptive anisotropic unstructured meshes hasbeen used for 3-D breakingwaves,which can modify and adapt unstructured meshestobetter represent theunderlying physicsof interfacial problems and reduce computational effort without sacrificing accuracy.
The numerical framework has been validated for a 2-D breaking wave over a sloping beach, in which a good agreement of the water surface profile between thesimulation and experimental measurementsis obtained.The present framework hasbeen further employed to investigate a 3-D breaking wave and its impact on a vertical cylinder along a slope. Development of plunging jet formation and complex interfacial structures during wave impact have been captured by the present method. The results presented hereestablished with sufficient confidencethat this method can be used to successfully model breaking waves and wave-structure interaction in a wide range of applications.
Acknowledgements
The first and second authorswould liketo acknowledge thefinancialsupport by the National Natural ScienceFoundation of China (Grant No.51490673),the Open Awardsof theState Key Laboratory of Coastal and Offshore Engineering. This work wasalsofunded by theEPSRC MEMPHIS multiphaseProgramme(Grant No.EP/K003976/1)and funding from the European Union Seventh Framework Programme (FP7/20072013) under grant agreement No.603663for the research project PEARL (Preparing for Extremeand Rareeventsin coastaL regions).
[1]Peregrine D. H. Breaking waves on beaches [J]. Annual Review of Fluid Mechanics, 1983, 15: 149-178.
[2]Banner M. L., Peregrine D. H. Wave breaking in deepwater [J]. Annual Review of Fluid Mechanics, 1993, 25:373-397.
[3] Mei C. C., Liu P. L. F. Surface-waves and coastal dynamics [J]. Annual Review of Fluid Mechanics,1993, 25:215-240.
[4]Kiger K. T., Duncan J. H. Air-entrainment mechanisms in plunging jets and breaking waves [J]. Annual Review of Fluid Mechanics, 2012, 44: 563-596.
[5]Lin P. Numericalmodeling of water waves:An introduction to engineersand scientists[M].London,UK:Taylor and Francis, 2008.
[6]McSherry R.J.,Chua K.V.,Stoesser T.Largeeddy simulation of free-surfaceflows [J]. Journal of Hydrodynamics, 2017, 29(1): 1-12.
[7]Lin P., Liu P. L. F. A numerical study of breaking waves in thesurf zone[J]. Journal of Fluid Mechanics,1998,359: 239-264.
[8]Bradford S. F. Numerical simulation of surf zone dynamics [J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2000, 126(1): 1-13.
[9]Zhao Q., Armfield S., Tanimoto K. Numerical simulation of breaking waves by a multi-scale turbulence model [J].Coastal Engineering, 2004, 51(1): 53-80.
[10] Shao S. Simulation of breaking wave by SPH method coupled with kε-model [J].Journal of Hydraulic Research, 2006, 44(3): 338-349.
[11] Christensen E. D., Deigaard R. Large eddy simulation of breaking waves[J].Coastal Engineering,2001,42(1):53-86.
[12] Watanabe Y., Saeki H., Hosking R. J. Three-dimensional vortex structuresunder breaking waves[J]. Journal of Fluid Mechanics, 2005, 545: 291-328.
[13] Wang Z., Zou Q., Reeve D. E. Simulation of spilling breaking wavesusing a twophaseflow CFDmodel [J].Computers and Fluids, 2009, 38(10): 1995-2005.
[14] Xie Z. Two-phase flow modelling of spilling and plunging breaking waves [J].Applied Mathematical Modelling,2013, 37(6): 3698-3713.
[15] Xie Z. Numerical study of breaking waves by a two-phase flow model [J].International Journal for Numerical Methods in Fluids, 2012, 70(2): 246-268.
[16] Xie Z. Numerical modelling of wind effects on breaking solitary waves [J].EuropeanJournal of Mechanics-B/Fluids, 2014, 43: 135-147.
[17] Xie Z. Numerical modelling of wind effects on breaking waves in the surf zone [J]. Ocean Dynamics, 2017, DOI:10.1007/s10236-017-1086-8(in Press).
[18] Lubin P., Vincent S., Abadie S. et al. Three-dimensional large eddy simulation of air entrainment under plunging breaking waves[J].Coastal Engineering,2006,53(8):631-655.
[19] Lakehal D., Liovic P. Turbulence structure and interaction with steep breaking waves [J]. Journal of Fluid Mechanics,2011, 674: 522-577.
[20]Xie Z.A two-phase flow model for three-dimensional breaking waves over complex topography [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2015, 471(2180): 20150101.
[21] Pavlidis D., Gomes J. L. M. A., Xie Z. et al. Compressive advection and multi-component methodsfor interfacecapturing [J]. International Journal of Numerical Methods in Fluids, 2016, 80(4): 256-282.
[22] Xie Z.,Pavlidis D.,SalinasP.et al. A balanced-force control volume finite element method for interfacial flows with surface tension using adaptive anisotropic unstructured meshes [J].Computersand Fluids,2016,138:38-50.
[23] Pain C. C., Umpleby A. P., de Oliveira C. R. E.et al.Tetrahedral mesh optimisation and adaptivity for steady-state and transient finite element calculations[J].Computer Methods in Applied Mechanics and Engineering, 2001, 190(29-30): 3771-3796.
[24] Xie Z., Pavlidis D., Percival J. R. et al. Adaptive unstructured mesh modelling of multiphase flows [J]. International Journal of Multiphase Flow, 2014, 67: 104-110.
[25] Pavlidis D., Xie Z., Percival J. R. et al. Two- and threephase horizontal slug flow simulations using an interfacecapturing compositional approach [J]. International Journal of Multiphase Flow, 2014, 67: 85-91.
[26] Nowak E., Xie Z., Kovalchuk N. M. et al. Bulk advection and interfacial flows in the binary coalescenceof surfactant-laden and surfactant-free drops [J]. Soft Matter,2017, 13: 4616-4628.
[27] Adebayo I., Xie Z.,Che Z.et al.Doubly-excited pulse waves on thin liquid films flowing down an inclined plane:An experimental and numerical study [J]. Physical Review E, 2017, 96: 013118.
[28] Xie Z., Hewitt G. F., Pavlidis D. et al. Numerical study of three-dimensional droplet impact on a flowing liquid film in annular two-phase flow [J]. Chemical Engineering Science, 2017, 166: 303-312.
[29] Li Y. Tsunamis: Non-breaking and breaking solitary wave run-up[D]. Doctoral Thesis, Pasadena, USA: California Institute of Technology, 2000.
June 6, 2017, Revised July 29, 2017)
* Biography: Zhihua Xie (1980-), Male, Ph. D., Lecturer
- 水動力學研究與進展 B輯的其它文章
- On the clean numerical simulation (CNS) of chaotic dynamic systems *
- BEM for wave interaction with structures and low storage accelerated methods for large scale computation *
- Flow-pipe-soil coupling mechanisms and predictions for submarine pipeline instability *
- Simulation of flows with moving contact lines on a dual-resolution Cartesian grid using a diffuse-interface immersed-boundary method *
- On the hydrodynamics of hydraulic machinery and flow control *
- A 3-D SPH model for simulating water flooding of a damaged floating structure *

