云南省玉溪第一中學(xué)(653100)武增明

函數(shù)中兩動(dòng)點(diǎn)間的距離的最值問(wèn)題

云南省玉溪第一中學(xué)(653100)武增明

函數(shù)中兩個(gè)動(dòng)點(diǎn)之間的距離的最值(取值范圍)問(wèn)題歸納起來(lái)主要有三類型:(1)兩個(gè)動(dòng)點(diǎn)分別在兩個(gè)函數(shù)圖象上;(2)兩個(gè)動(dòng)點(diǎn)分別在一個(gè)函數(shù)圖象和一個(gè)圓錐曲線上;(3)兩個(gè)動(dòng)點(diǎn)分別在一個(gè)函數(shù)圖象和一條直線上.下面通過(guò)例子具體談一談函數(shù)中兩動(dòng)點(diǎn)間的距離的最值(取值范圍)的三種類型的探求方法.

1.兩個(gè)動(dòng)點(diǎn)分別在兩個(gè)函數(shù)圖象上

兩個(gè)動(dòng)點(diǎn)P,Q分別在兩個(gè)函數(shù)圖象上,求這兩個(gè)動(dòng)點(diǎn)P,Q之間的距離的最值(取值范圍).解決這類問(wèn)題的方法是,把問(wèn)題轉(zhuǎn)化為求直線l1和直線l2平行且直線l1與函數(shù)圖象相切的切點(diǎn)到直線l2的距離,即把問(wèn)題轉(zhuǎn)化為求切點(diǎn)到直線的距離.

例1.(2012年高考全國(guó)新課標(biāo)卷理科第12題)設(shè)點(diǎn)P在曲線y=ex上,點(diǎn)Q在曲線y=ln(2x)上,則|PQ|的最小值為( )

例2.設(shè)點(diǎn)P在曲線y=ex上,點(diǎn)Q在曲線

(x＞0)上,則|PQ|的最小值是( )

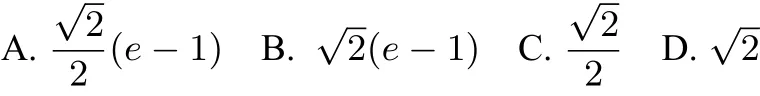
解析 因?yàn)閥=ex的反函數(shù)是y=lnx,兩個(gè)函數(shù)的圖象關(guān)于直線y=x對(duì)稱,如圖1.所以曲線y=ex上的點(diǎn)P到直線 y=x的距離等于點(diǎn)P關(guān)于直線y=x的對(duì)稱點(diǎn)P′到直線y=x的距離.

圖1

當(dāng)0＜ x ＜ 1時(shí),f′(x)＜ 0;當(dāng)x ＞ 1時(shí),f′(x)＞ 0,所以函數(shù)f(x)在 (0,+∞)上有最小值f(1)=0,則當(dāng)x＞0時(shí),除(1,0)點(diǎn)外函數(shù) y=lnx的圖象恒在的圖象的上方,在 (1,0)處兩曲線相切.

求曲線y=ex上的點(diǎn)P與曲線上的點(diǎn)Q的距離的最小值,可看作是求曲線 y=lnx上的點(diǎn)P′與點(diǎn)Q到直線y=x的距離的和的最小值,而函數(shù)y=lnx與在x=1處的導(dǎo)數(shù)都是1,說(shuō)明與直線y=x平行的直線與兩曲線切于同一點(diǎn)(1,0),則|PQ|的最小值為點(diǎn)(1,0)到直線y=x距離的2倍,所以|PQ|的最小值為故選D.

評(píng)注 求兩個(gè)函數(shù)圖象上兩個(gè)動(dòng)點(diǎn)間的距離的最小值,顯然沒(méi)法利用兩點(diǎn)間的距離公式計(jì)算,結(jié)合函數(shù)y=ex圖象上的點(diǎn)關(guān)于直線y=x的對(duì)稱點(diǎn)在其反函數(shù)的圖象上把問(wèn)題轉(zhuǎn)化為求曲線y=lnx上的點(diǎn)與上的點(diǎn)到直線y=x的距離之和的最小值問(wèn)題,而與直線y=x平行的直線同時(shí)與曲線y=lnx和切于同一點(diǎn)(1,0),所以P,Q間的距離的最小值為點(diǎn)(1,0)到直線y=x距離的2倍.

2 兩個(gè)動(dòng)點(diǎn)分別在一個(gè)函數(shù)圖象和一個(gè)圓錐曲線上

兩個(gè)動(dòng)點(diǎn)P,Q分別在一個(gè)函數(shù)圖象和一個(gè)圓錐曲線上,求這兩個(gè)動(dòng)點(diǎn)P,Q之間的距離的最值(取值范圍).解決此類問(wèn)題的方法有二種,方法1:若兩個(gè)動(dòng)點(diǎn)P,Q分別在一個(gè)函數(shù)圖象和一個(gè)圓上,則把問(wèn)題轉(zhuǎn)化為求直線l與函數(shù)圖象相切于點(diǎn)A,且l垂直于點(diǎn)A與圓心B連線時(shí),A和圓心B之間的距離.方法2:若兩個(gè)動(dòng)點(diǎn)P,Q分別在一個(gè)函數(shù)圖象和一個(gè)橢圓或雙曲線或拋物線上,則把問(wèn)題轉(zhuǎn)化為求與函數(shù)圖象相切的直線l1和與橢圓(雙曲線或拋物線)相切的直線l2,和平行線l1,l2的之間的距離.

例3.已知點(diǎn)P為函數(shù)f(x)=lnx的圖象上任意一點(diǎn),點(diǎn)Q為圓上任意一點(diǎn),則線段PQ的長(zhǎng)度的最小值為( )

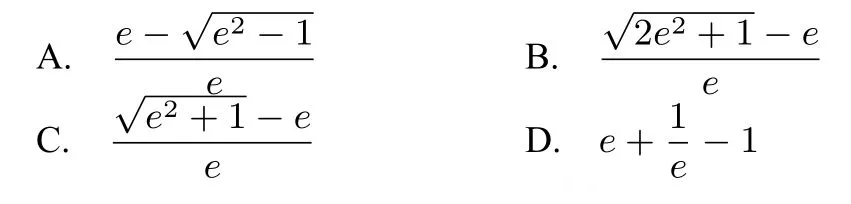
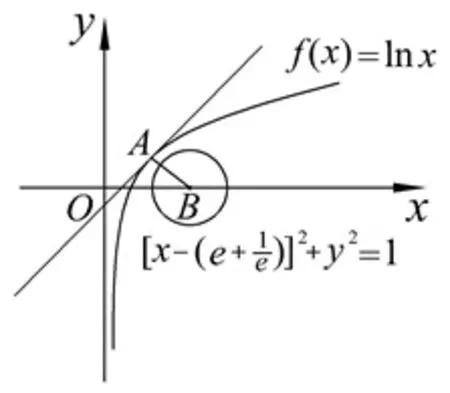
圖2

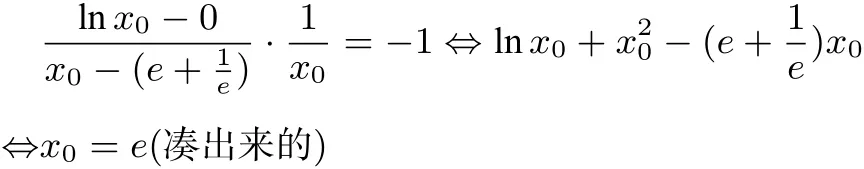
故A(e,1).從而

故而選C.

例4. 如果P是函數(shù)y=f(x)圖象上的點(diǎn),Q是函數(shù)y=g(x)圖象上的點(diǎn),且P,Q兩點(diǎn)之間的距離|PQ|能取到最小值,那么將d稱為函數(shù)y=f(x)與y=g(x)之間的距離.按這個(gè)定義,函數(shù)之間的距離是___.

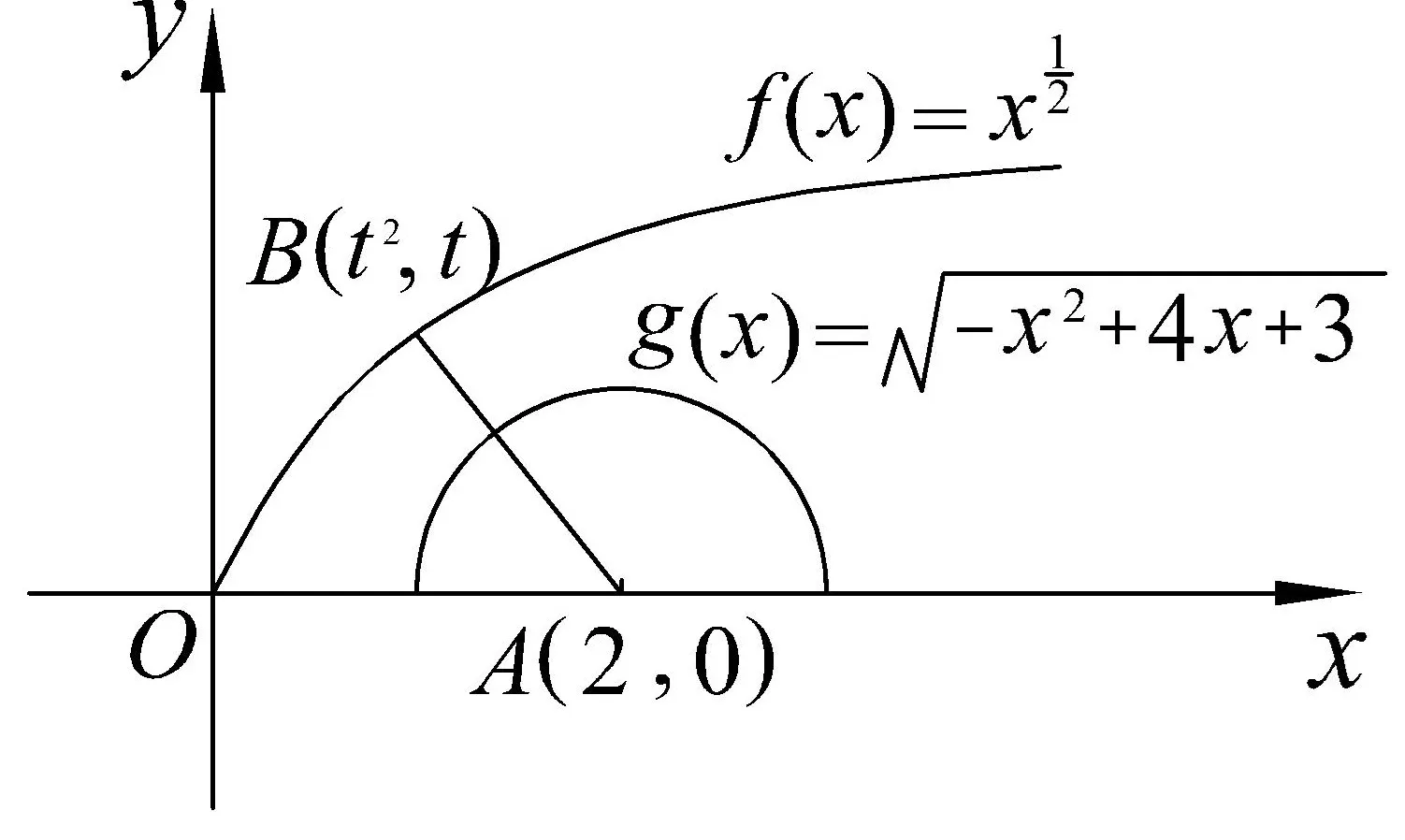
圖3

設(shè)動(dòng)點(diǎn)B(t2,t)是y=f(x)圖象上任意一點(diǎn),則|AB|=當(dāng)|AB|取得最小值

評(píng)注 此題用上述例3的解法很易求解.

3 兩個(gè)動(dòng)點(diǎn)分別在一個(gè)函數(shù)圖象和一條直線上

兩個(gè)動(dòng)點(diǎn)P,Q分別在一個(gè)函數(shù)圖象和一條直線l上,求這兩個(gè)動(dòng)點(diǎn)P,Q之間的距離的最值(取值范圍).解決這類問(wèn)題的方法是,把問(wèn)題轉(zhuǎn)化為求直線l1與函數(shù)圖象相切,且 l1平行l(wèi)的切點(diǎn)到直線l的距離.

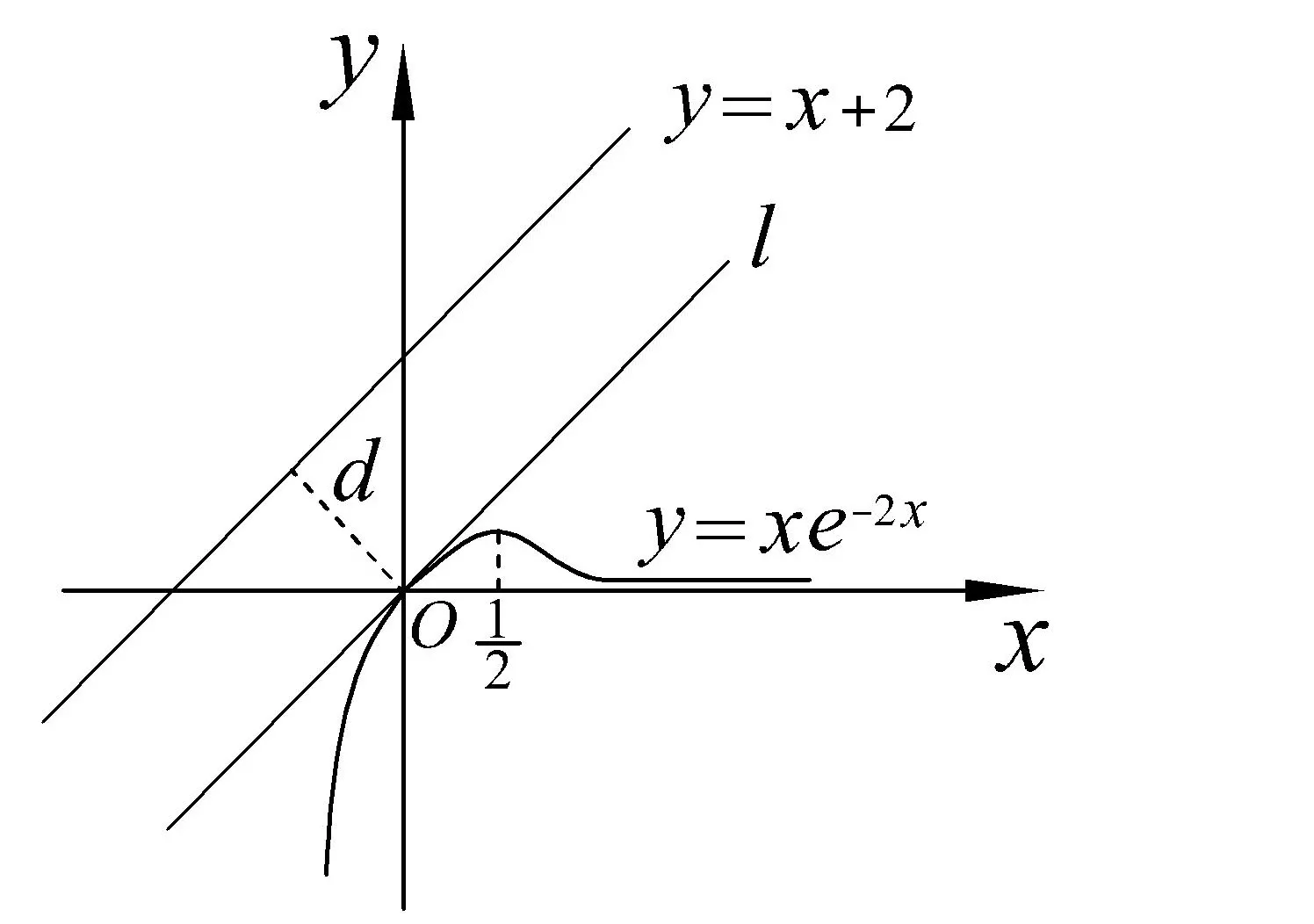
圖4

例5設(shè)點(diǎn)P,Q分別是曲線y=xe?2x和直線y=x+2上的動(dòng)點(diǎn),則P,Q兩點(diǎn)間的距離的最小值是_____.e?2x0?2x0e?2x0,故e?2x0?x0e?2x0=1,由此湊出 x0=0,從而A(0,0),于是點(diǎn)A(0,0)到直線y=x+2的距離為故而

簡(jiǎn)解 設(shè)與直線y=x+2平行的直線l和曲線y=xe?2x相切的切點(diǎn)為A(x,xe?2x),如圖4,則因?yàn)?y′=(xe?2x)′=e?2x?2xe?2x,所以 kl=

4 問(wèn)題變式

在這里,筆者給出如下一組變式題,旨在供同仁在教學(xué)過(guò)程中作參考和同學(xué)們?cè)趯W(xué)習(xí)此問(wèn)題時(shí)作練習(xí).

1.若點(diǎn)P,Q分別在函數(shù)y=ex和函數(shù)y=lnx的圖象上,則P,Q兩點(diǎn)間的距離的最小值是___

2.若P,Q分別是函數(shù)y=lnx?x2,y=x+2的圖象上的動(dòng)點(diǎn),則|PQ|2的最小值為____.(8)

3.在函數(shù)f(x)=ln(2x?1)圖象上求一點(diǎn)P,使得點(diǎn)P到直線y=x+3的距離最短____

4.若P,Q分別是函數(shù)y=x2?lnx,y=x?2的圖象上的動(dòng)點(diǎn),則|PQ|的最小值為____

5.函數(shù)f(x)=ex+x2+x+1的圖象M關(guān)于直線2x?y?3=0對(duì)稱的圖象為N,P,Q分別是兩圖象上的動(dòng)點(diǎn),則|PQ|的最小值為___

6.如果P是函數(shù)y=f(x)圖象上的點(diǎn),Q是函數(shù)y=g(x)圖象上的點(diǎn),且P,Q兩點(diǎn)之間的距離|PQ|能取到最小值d,那么將d稱為函數(shù)y=f(x)與y=g(x)之間的距離.按這個(gè)定義,函數(shù)f和之間的距離是____

以上變式題解略,各題后面括號(hào)內(nèi)為答案.