傅金波,陳蘭蓀

(1.福建師范大學(xué)閩南科技學(xué)院,福建泉州362332)

(2.中國科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院數(shù)學(xué)研究所,北京100080)

具有垂直傳染和接觸傳染的傳染病模型的穩(wěn)定性研究

傅金波1,陳蘭蓀2

(1.福建師范大學(xué)閩南科技學(xué)院,福建泉州362332)

(2.中國科學(xué)院數(shù)學(xué)與系統(tǒng)科學(xué)研究院數(shù)學(xué)研究所,北京100080)

本文研究了一類具有垂直傳染和接觸傳染的傳染病模型.利用常微分方程定性與穩(wěn)定性方法,分析了該模型非負平衡點的存在性及其局部穩(wěn)定性.同時,利用LaSalle不變性原理和通過構(gòu)造適當(dāng)?shù)腖yapunov函數(shù),獲得了平凡平衡點、無病平衡點和地方病平衡點全局漸近穩(wěn)定的充分條件.結(jié)果表明當(dāng)基本再生數(shù)小于等于1時,所有種群趨于滅絕;當(dāng)基本再生數(shù)大于1和病毒主導(dǎo)再生數(shù)小于1時,病毒很快被清除;當(dāng)基本再生數(shù)大于1和病毒主導(dǎo)再生數(shù)大于1以及滿足一定條件時,病毒持續(xù)流行并將成為一種地方病.

傳染病模型;非負平衡點;全局漸近穩(wěn)定性

1　引言

生物動力系統(tǒng)的動力學(xué)性質(zhì)歷來受到學(xué)術(shù)界的重視[1-5].然而,考慮疾病對生物種群影響的相對較少.近年來,在生物動力系統(tǒng)中含有疾病影響因素的傳染病模型已有了可喜的研究成果[6-12].在帶有常數(shù)輸入率的傳染病模型中,基本再生數(shù)是一個重要的閥值,當(dāng)基本再生數(shù)小于1時,疾病將趨于滅絕;當(dāng)基本再生數(shù)大于1時,疾病將持續(xù)存在[13-14].但在輸入率不是常數(shù)情形下的傳染病模型中,系統(tǒng)卻存在著后向分支現(xiàn)象[15].基于上述文獻的建模機理,本文用N(t)=S(t)+I(t)表示t時刻的生物種群總數(shù),S(t)表示該種群中的易感類,I(t)表示該種群中的染病類,建立具有垂直傳染和接觸傳染的傳染病模型如下

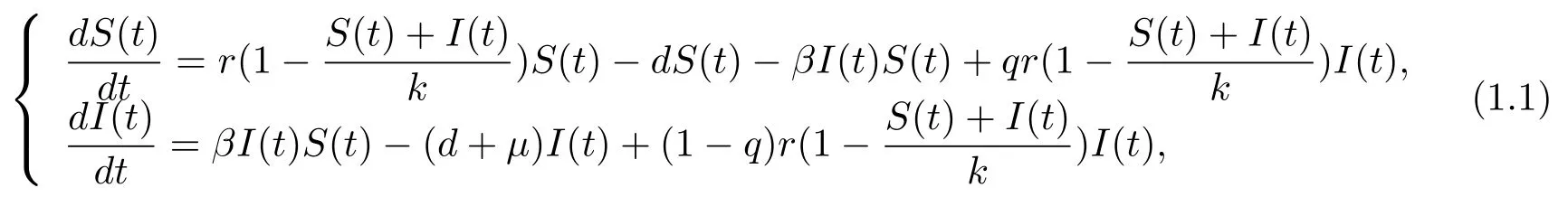
其中r為增長率,k為環(huán)境容納量,d為自然死亡率,β為接觸的比例系數(shù),q為染病類中新生個體未染病的比例系數(shù)0＜q＜1,1-q為染病類中新生個體的染病速率,μ為因病死亡率,并且所有參數(shù)均為正數(shù).

由N(t)=S(t)+I(t),模型(1.1)可化為如下等價系統(tǒng)

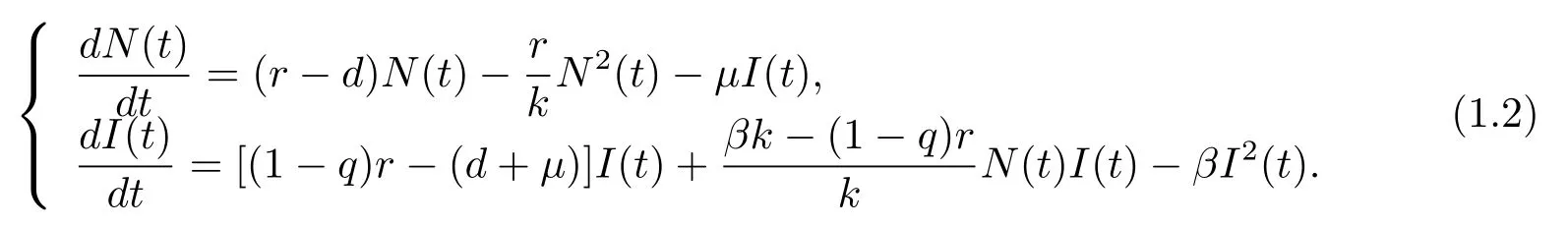
易見,系統(tǒng)(1.2)的可行域為D={(N(t),I(t))∈R2|0≤N(t)≤k,0≤I(t)≤k}.本文主要在可行域D內(nèi)研究系統(tǒng)(1.2)的動力學(xué)性質(zhì).

2　平衡點的存在性

系統(tǒng)(1.2)的非負平衡點應(yīng)滿足下面的代數(shù)方程組

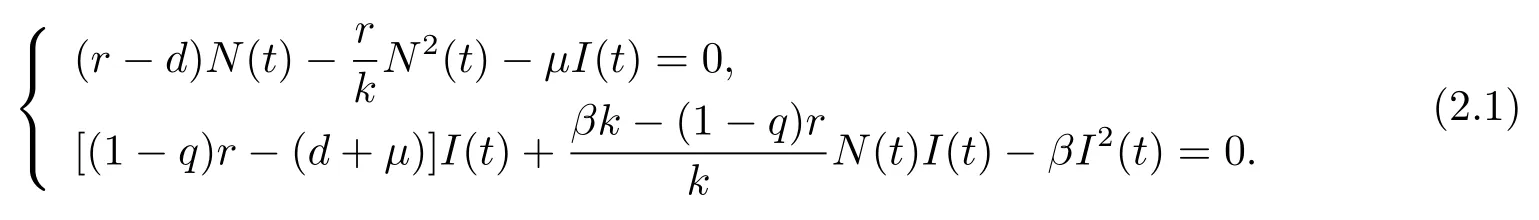
為著以下證明,定義基本再生數(shù)和病毒主導(dǎo)再生數(shù)分別為

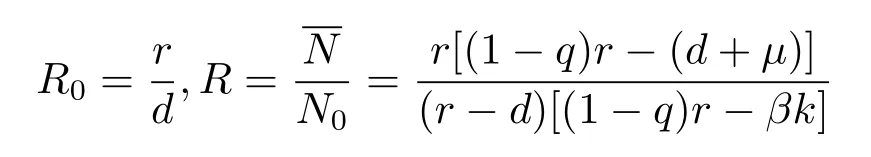
以及如下記號

由方程組(2.1)易得如下結(jié)論.

定理2.1系統(tǒng)(1.2)存在平凡平衡點O(0,0);當(dāng)R0＞1時,還存在無病平衡E0(N0,0).

下面討論系統(tǒng)(1.2)在域D內(nèi)地方病平衡點的存在性.一方面,當(dāng)N0,I0時,由方程組(2.1)的第一個方程得等傾線

可見,當(dāng)R0＞1時,f(N)是過O(0,0)和E0(N0,0)的開口向下拋物線.

情形1若σ2＞1＞σ1或σ1＞1＞σ2,則＜0.

(I)當(dāng)R0＞σ2＞1＞σ1時,直線g(N)的斜率為正數(shù).

(II)當(dāng)R0＞σ1＞1＞σ2時,直線g(N)不在第一象限,此時f(N)與g(N)沒有正交點.

情形2若σi＜1或σi＞1,i=1,2,則＞0.

(III)當(dāng)R0＞1＞σi,i=1,2,時,直線g(N)的斜率為正數(shù).

(IV)當(dāng)R0＞σi＞1,i=1,2時,直線g(N)的斜率為負數(shù).

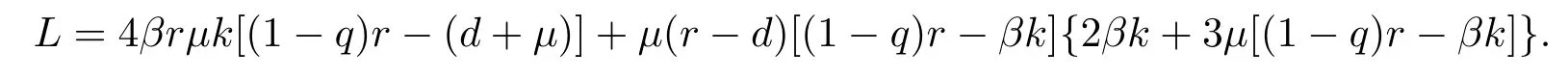
另一方面,由f(N)=g(N)得代數(shù)方程a2N2-a1N+a0=0,其中

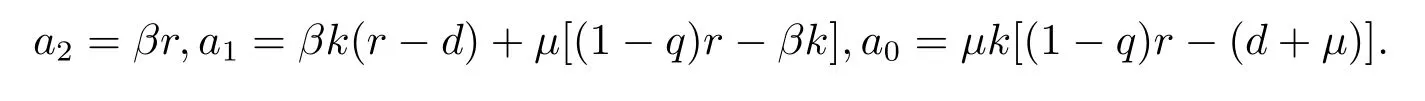
令

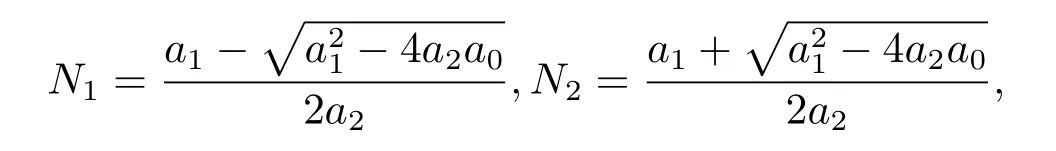
記正交點為E(N?,I?),記兩個正交點為Ωi(Ni,Ii),i=1,2.綜上分析,有如下結(jié)論.

定理2.2如果滿足下列條件

(1)R0＞σ2＞1＞σ1,βk(r-d)=2+μ[βk-(1-q)r];

(2)R0＞1＞σi,R＜1,i=1,2;

(3)R0＞σi＞1,R＜1,i=1,2;

(4)R0＞σi＞1,R＞1,{βk(r-d)}2=L,i=1,2

之一,系統(tǒng)(1.2)在域D內(nèi)部存在一個地方病平衡點E(N?,I?).

如果滿足下列條件

(1)R0＞σ2＞1＞σ1,βk(r-d)＞2+μ[βk-(1-q)r];

(2)R0＞σi＞1,R＞1,{βk(r-d)}2＞L,i=1,2

之一,系統(tǒng)(1.2)在域D內(nèi)部存在兩個地方病平衡點Ωi(Ni,Ii),i=1,2.

推論2.1如果R0＞σi＞1,R＞1,{βk(r-d)}2＞L,i=1,2或

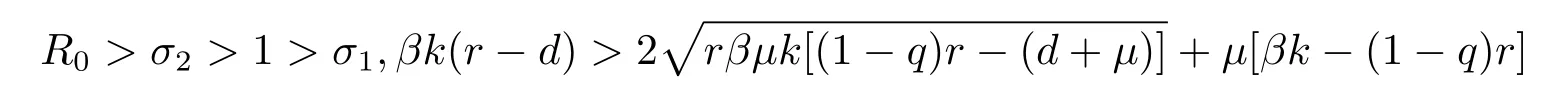
成立,系統(tǒng)(1.2)在域D內(nèi)存在一個后向分支.

3　平衡點的局部穩(wěn)定性

下面討論系統(tǒng)(1.2)的平凡平衡點、無病平衡點和地方病平衡點局部穩(wěn)定性.

定理3.1如果R0＜1(R0＞1),則系統(tǒng)(1.2)在域D上的平凡平衡點O(0,0)是局部穩(wěn)定(不穩(wěn)定).

證在點O(0,0)處,系統(tǒng)(1.2)的Jacobian矩陣為

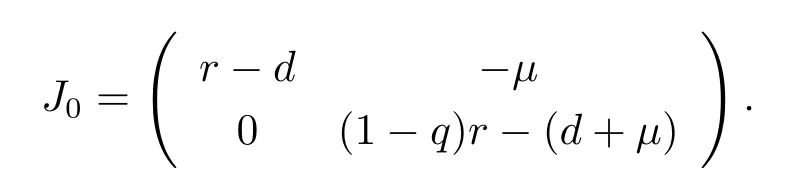
特征方程為(λ-r+d)[λ-(1-q)r-(d+μ)]=0,特征值為

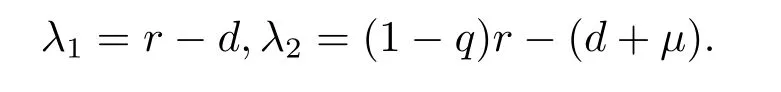
當(dāng)R0＜1時λ1＜0,λ2＜0,平凡平衡點O(0,0)是局部穩(wěn)定的;當(dāng)R0＞1時,因λ1＞0,平凡平衡點O(0,0)是不穩(wěn)定的.證畢.

定理3.2當(dāng)R0＞1＞σi,i=1,2時,若R＞1(R＜1),則系統(tǒng)(1.2)在域D上的無病平衡點E0(N0,0)是局部穩(wěn)定(不穩(wěn)定);當(dāng)R0＞σi＞1,i=1,2時,若R＜1(R＞1),則系統(tǒng)(1.2)在域D上的無病平衡點E0(N0,0)是局部穩(wěn)定(不穩(wěn)定).

證在點E0(N0,0)處,系統(tǒng)(1.2)的Jacobian矩陣為

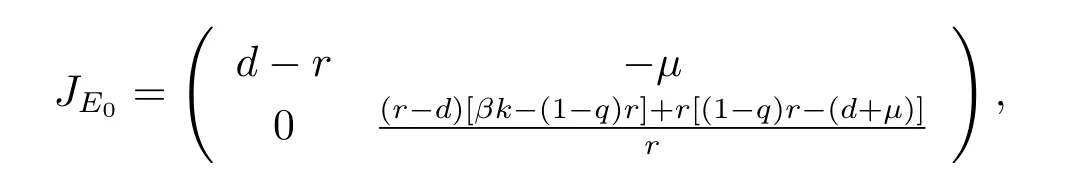
特征方程為

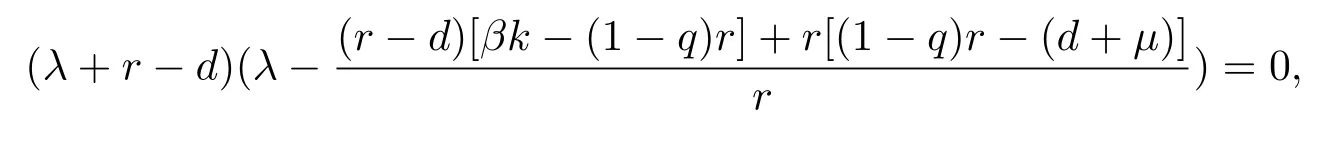
得特征值

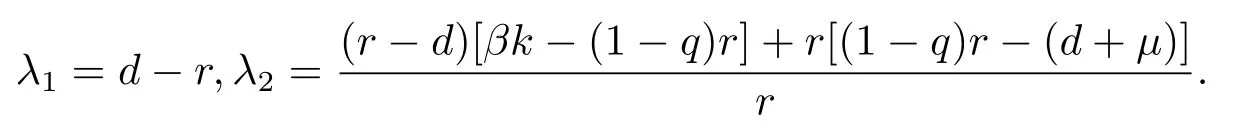
當(dāng)R0＞1＞σi,i=1,2且R＞1時,總有

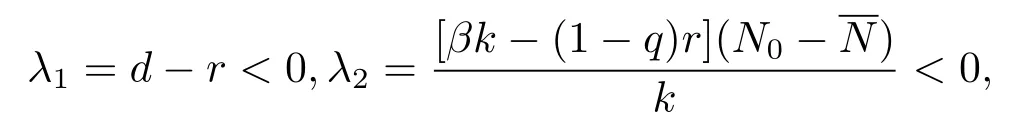
或者當(dāng)R0＞σi＞1,i=1,2且R＜1時,也總有

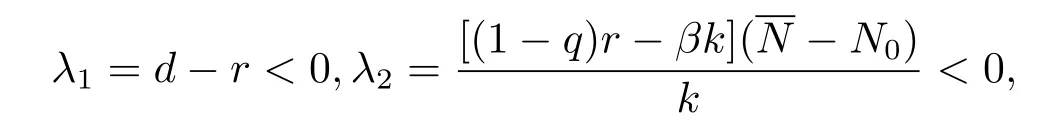
故無病平衡點E0(N0,0)是局部穩(wěn)定的;當(dāng)R0＞1＞σi,i=1,2且R＜1或R0＞σi＞1,i= 1,2且R＞1時,λ2＞0無病平衡點E0(N0,0)是不穩(wěn)定的.證畢.

定理3.3如果R0＞σi＞1,R＜1,i=1,2且rβ(2N?-N0)＞μ[(1-q)r-βk]或R0＞1＞σi,R＜1,i=1,2且2N?＞N0,則系統(tǒng)(1.2)在域D內(nèi)的地方病平衡點E(N?,I?)是局部穩(wěn)定的;否則,地方病平衡點E(N?,I?)是不穩(wěn)定的.

證在E(N?,I?)點處,系統(tǒng)(1.2)的Jacobian矩陣為

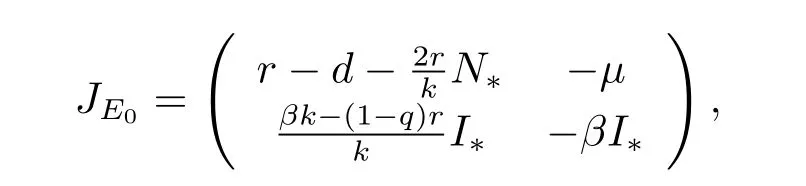
特征方程為λ2+b1λ-b0=0,其中

特征值為

同時,注意y1=λ2是開口向上拋物線,y2=-b1λ+b0是直線,如果R0＞1＞σi,R＜1,i= 1,2且2N?＞N0或R0＞σi＞1,R＜1,i=1,2且rβ(2N?-N0)＞μ[(1-q)r-βk]成立,則b1＞0,b0＜0,進而特征方程具有兩個負實根或一對帶負實部的復(fù)根,系統(tǒng)(1.2)在域D內(nèi)的地方病平衡點E(N?,I?)是局部穩(wěn)定的.否則,即不滿足上述條件中任意一條,系統(tǒng)(1.2)在域D內(nèi)的地方病平衡點E(N?,I?)是不穩(wěn)定的.證畢.

4　平衡點的全局漸近穩(wěn)定性

定理4.1如果R0≤1且σi＞1,i=1,2或R0≤1且σi＜1,i=1,2,則系統(tǒng)(1.2)在域D內(nèi)的平凡平衡點O(0,0)是全局漸近穩(wěn)定的.

證當(dāng)R0≤1且σi＞1,i=1,2時,定義Lyapunov函數(shù)V(t)=沿著系統(tǒng)(1.2)的解直接計算V(t)的右上導(dǎo)數(shù)有

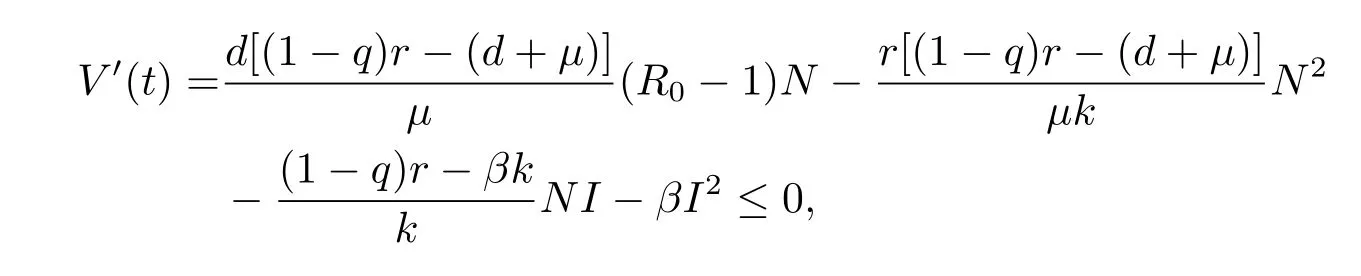
使得V＇(t)=0只有平凡平衡點O(0,0),即系統(tǒng)(1.2)的最大不變集是平凡平衡點O(0,0)且它是全局吸引的.根據(jù)定理3.1和LaSalle不變性原理[16],系統(tǒng)(1.2)在域D內(nèi)的平凡平衡點O(0,0)是全局漸近穩(wěn)定的.

當(dāng)R0≤1且σi＜1,i=1,2,時,定義Lyapunov函數(shù)V0(t)=N(t)+I(t),沿著系統(tǒng)(1.2)的解直接計算V0(t)的右上導(dǎo)數(shù)有

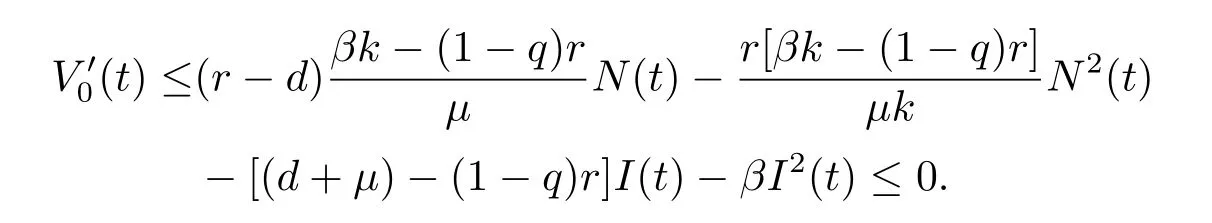
類似于上述方法,可知系統(tǒng)(1.2)在域D內(nèi)的平凡平衡點O(0,0)是全局漸近穩(wěn)定的.證畢.

定理4.2如果R0＞σi＞1,R＜1,i=1,2或R0＞1＞σi,R＞1,i=1,2,則系統(tǒng)(1.2)在域D內(nèi)的無病平衡點E0(N0,0)是全局漸近穩(wěn)定的.

證將系統(tǒng)(1.2)改寫為等價系統(tǒng)

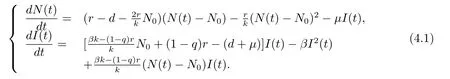
(1)當(dāng)R0＞σi＞1,R＜1,i=1,2時,構(gòu)造Lyapunov函數(shù)

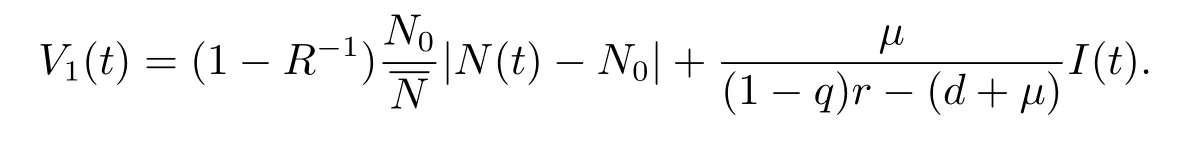
沿著系統(tǒng)(4.1)的解直接計算V1(t)的右上導(dǎo)數(shù)有

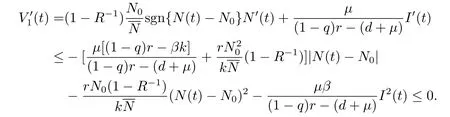
易見{(N,I)T∈D:(t)=0}={(N0,0)},即無病平衡點E0(N0,0)為最大不變集,而且它是全局吸引的.根據(jù)定理3.2和LaSalle不變性原理[16],系統(tǒng)(1.2)在域D內(nèi)的無病平衡點E0(N0,0)是全局漸近穩(wěn)定的.

(2)當(dāng)R0＞1＞σi,R＞1,i=1,2時,構(gòu)造Lyapunov函數(shù)

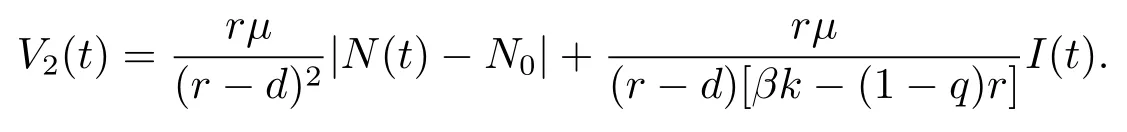
沿著系統(tǒng)(4.1)的解直接計算V2(t)的右上導(dǎo)數(shù)有

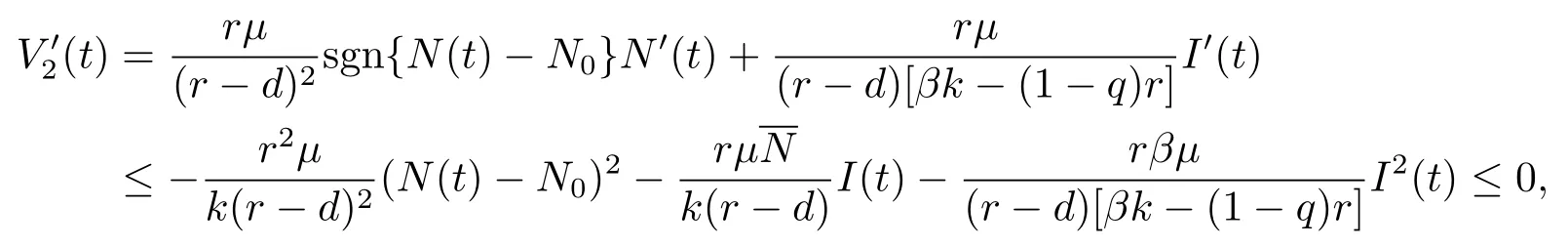
同樣地,系統(tǒng)(1.2)在域D內(nèi)的無病平衡點E0(N0,0)是全局漸近穩(wěn)定的.證畢.

定理4.3如果(1)R0＞σi＞1,R＜1,i=1,2,rβ(2N?-N0)＞μ[(1-q)r-βk]且σi,R＜1,i=1,2,2N?＞N0且[(d+μ)-(1-q)r]+2βI?≥[βk-(1-q)r]則系統(tǒng)(1.2)在域D內(nèi)的地方病平衡點E(N?,I?)是全局漸近穩(wěn)定的.

證將系統(tǒng)(1.2)改寫為如下等價系統(tǒng)

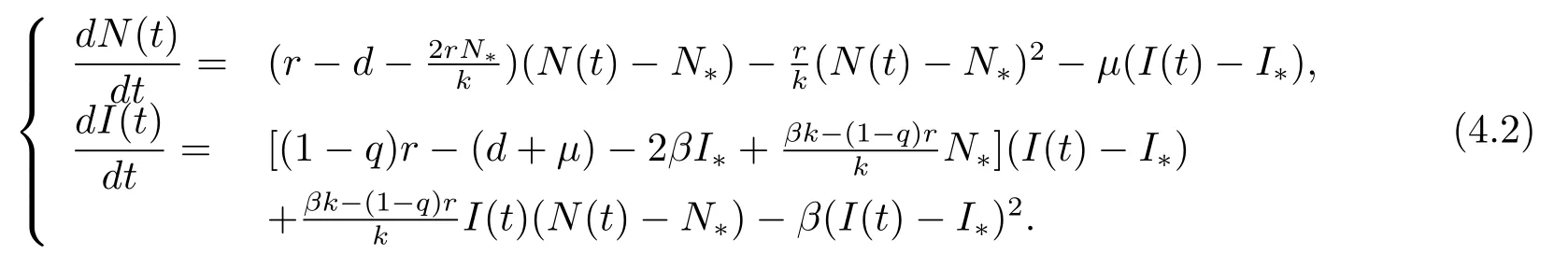
在條件(1)下,定義Lyapunov函數(shù)

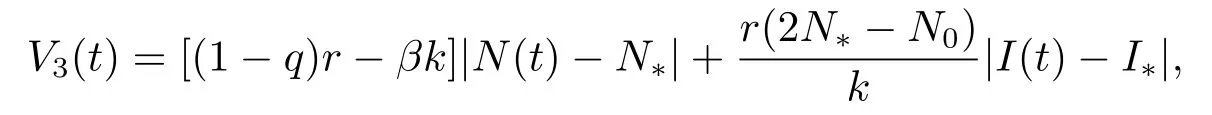
沿著系統(tǒng)(4.2)的解計算V3(t)的右上導(dǎo)數(shù)有

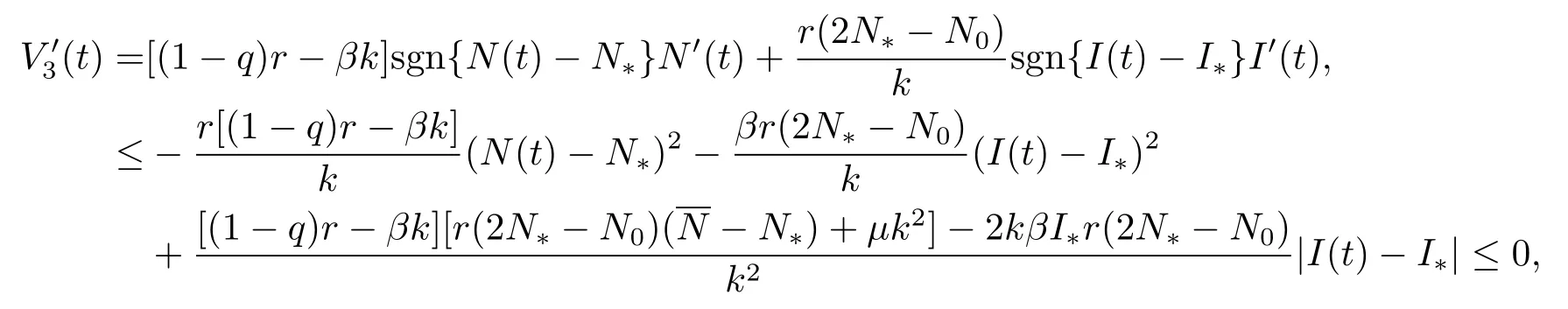
在條件(2)下,定義Lyapunov函數(shù)

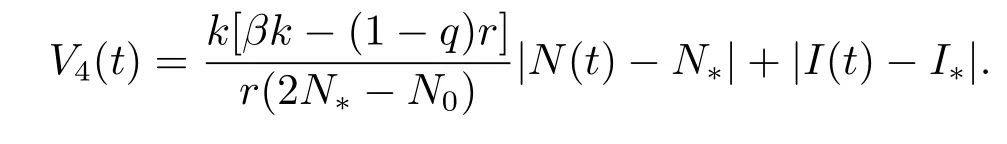
沿著系統(tǒng)(4.2)的解計算V4(t)的右上導(dǎo)數(shù)有

其中在條件(2)下

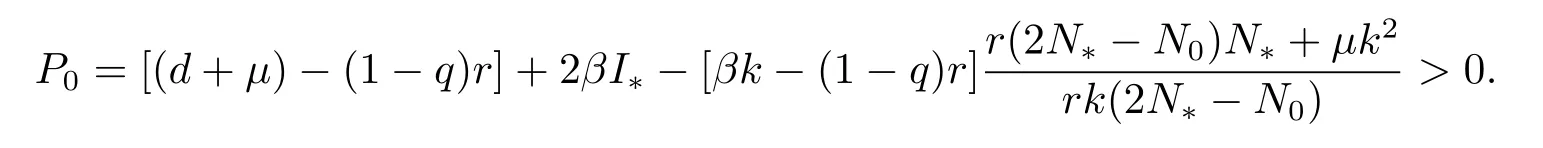
同樣地,在條件(2)下系統(tǒng)(1.2)在域D內(nèi)的地方病平衡點E(N?,I?)是全局漸近穩(wěn)定的.

5　結(jié)論

研究結(jié)果表明:基本再生數(shù)是該系統(tǒng)中生物種群持續(xù)生存的閥值,病毒主導(dǎo)再生數(shù)是疾病在該系統(tǒng)中是否流行的閥值.如果滿足定理4.1的條件,則該系統(tǒng)中的生物種群將趨于滅絕;如果滿足定理4.2的條件,則該系統(tǒng)中的病毒很快將被清除;如果滿足定理4.3的條件,則該系統(tǒng)的易感類和染病類均將持續(xù)存在,并將趨于一組穩(wěn)定的定值上,此時流行性疾病成為一種地方病.關(guān)于有兩個地方病平衡點情況不予討論,顯然它們是不穩(wěn)定的.據(jù)此,在生物動力系統(tǒng)的流行病學(xué)分析中,要持續(xù)關(guān)注基本再生數(shù)和疾病流行的閥值,尤其是垂直傳染和接觸傳染等影響因素.

[1]崔景安.時滯Lotka-Volterra系統(tǒng)的持久性和周期解[J].數(shù)學(xué)學(xué)報,2000,47(1):511-519.

[2]惠靜,陳蘭蓀.脈沖時滯微分方程的周期性和穩(wěn)定性[J].數(shù)學(xué)學(xué)報,2005,48(6):1137-1144.

[3]Chen Fengde,Shi Jinlin,Chen Xiaoxing.Periodicity in a Lotka-Volterra Facultative Mutualism system with several delays[J].Chinese J.Engin.Math.,2004,21(3):1005-3085.

[4]葉丹,范猛.具有脈沖的三種群捕食者-食餌鏈系統(tǒng)正周期解的存在性[J].東北師大學(xué)報(自然科學(xué)版), 2004,36(4):1-10.

[5]趙明,程榮福.一類具生物控制和比率型功能反應(yīng)的食物鏈系統(tǒng)周期解的存在性[J].吉林大學(xué)學(xué)報(理學(xué)版),2009,47(4):730-736.

[6]Ma Zhien,Liu Jiangping,Li Jia.Stability analysis for differential infectivity epidemic models[J]. Nonl.Anal.:Real World Appl.,2003,4:841-856.

[7]Wang Wendi,Ruan S.Bifurcation in an epidemic model with constant removal rate of the infectives[J].Math.Anal.Appl.,2004,291:775-793.

[8]Huang Yunjin,Chen Fengde,Li Zhong.Stability analysis of a prey-predator model with holling type III response function incorporating a prey refuge[J].Appl.Math.Comput.,2006,182(1):672-683. 47(5):511-517.

[9]Wang Wendi.Backward bifurcation of an epidemic model with treatment[J].Math.Bios.,2006,201: 58-71.

[10]Cui Jingam,Mu Xiaoxia,Wan Hui.Saturation recovery leads to multiple endemic equilibria and backward bifurcation[J].J.The.Biol.,2008,254:275-283.

[11]Chen Liujuan,Chen Fengde.Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge[J].Nonl.Anal.:Real World Appl.,2010, 11(1):246-252.

[12]劉細憲,李必文,陳伯山.食餌帶疾病的捕食模型的全局穩(wěn)定性[J].數(shù)學(xué)雜志,2015,35(1):85-94.

[13]Ma Zhien,Liu Jiangping,Li Jia.Stability analysis for differential infectivity epidemic models[J]. Nonl.Anal.:Real World Appl.,2003,4:841-856.

[14]朱璣,李維德,朱凌峰.基于SIR傳染病模型的不同控制策略比較[J].北華大學(xué)學(xué)報(自然科學(xué)版), 2011,12(3):265-269.

[15]唐曉明,薛亞奎.具有飽和治療函數(shù)與密度制約的SIS傳染病模型的后向分支[J].數(shù)學(xué)的實踐與認識, 2010,40(24):241-246.

[16]馬知恩,周義倉.傳染病動力學(xué)的數(shù)學(xué)建模與研究[M].北京:科學(xué)出版社,2004.

2010 MR Subject Classification:34D20;34D23

ON THE STABILITY PROPERTY OF A EPIDEMIC MODEL WITH VERTICAL TRANSMISSION AND CONTACT TRANSMISSION

FU Jin-bo1,CHEN Lan-sun2
(1.Minnan Science and Technology Institute Fujian Normal University,Quanzhou 362332,China)
(2.Academy of Mathematics and Systems Science,Chinese Academy of Sciences, Beijing 100080,China)

In this paper,a class of epidemic model with vertical transmission and contact transmission is established.By means of qualitative method and stability method of ordinary differential equations,the model and the existence of nonnegative equilibrium point are analyzed. And by constructing proper Lyapunov function and LaSalle invariance principle,sufficient conditions of the global asymptotic stability of the trivial equilibrium point,disease-free equilibrium point and endemic equilibrium point are obtained.The results show that when the basic reproduction number is less than or equal to 1,all populations tend to be extinct;when the basic reproduction number is greater than 1 and virus dominant reproduction number is less than 1, the viruses was quickly cleared;when the basic reproduction number is greater than 1 and virus dominant reproduction number is greater than 1 and satisfy certain conditis,the viruses continue to prevail and will become a local disease.

epidemic model;nonnegative equilibrium point;global asymptotic stability

MR(2010)主題分類號:34D20;34D23O175.13

A

0255-7797(2016)06-1283-08

?2015-11-30接收日期:2016-06-28

國家自然科學(xué)基金(11371306);福建省教育廳自然科學(xué)基金(JA13370;JAT160676);福建師范大學(xué)閩南科技學(xué)院青年骨干教師重點培養(yǎng)對象(mkq201006).

傅金波(1978-),男,福建南安,副教授,主要研究方向:生物數(shù)學(xué).