Laplacian Spectral Characterization of Graphs with Exactly Two Laplacian Eigenvalues Greater than Two?
MA Xiaoling,WEN Fei
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
Abstract: In this paper,we prove that all connected graphs with exactly two Laplacian eigenvalues greater than two are determined by their Laplacian spectra.
Key words:Laplacian spectrum;L-cospectral graph;two Laplacian eigenvalues greater than two;determined by the Laplacian spectrum
0 Introduction
The graphs considered in this paper are simple and undirected.LetG=(V(G),E(G))be a simple undirected graph with vertex setV(G)={v1,v2,…,vn}and edge setE(G),where its order and size are|V(G)|=n(G)=nand|E(G)|=m(G)=m.Denote bydi(G)the degree of a vertexviinG.We denote the diagonal matrix of vertex degrees byD(G)and denote the adjacency matrix byA(G).ThenL(G)=D(G)?A(G)is called the Laplacian matrix ofG.We use Φ(G;x)to denote the Laplacian characteristic polynomial ofL(G).Its eigenvalues will be called the Laplacian eigenvalues of graphG.Assume thatμ1(G)≥μ2(G)≥…≥μn(G)=0 are the Laplacian eigenvalues of the graphG.
TheLaplacian spectrumof the graphG,denoted by SpecL(G),is the multiset of its Laplacian eigenvalues.Two graphsGandHare said to beL-cospectral,denoted by SpecL(G)=SpecL(H)if they share the same Laplacian spectrum(i.e.,equal Laplacian characteristic polynomial).A graphGis said to bedetermined by the Laplacian spectrum(DLSfor short)if for any graphH,Φ(G;x)=Φ(H;x)implies thatHis isomorphic toG.The background of spectral graph theory and terminology not de fined can be found in[1]for references.
In 2003,van Dam and Haemers[2]proposed the question that which graphs are determined by their spectra?This seemstobeadifficultprobleminthetheoryofgraphspectra.Theexactcharacterizationofgraphswithsomeeigenvalue exceeding a given value is extensively studied,however,whether they are determined by their Laplacian spectra or not is less considered.Recently,Ma,Huang and Liu[3]proved that all unicyclic graphs with second largest eigenvalue does not exceed 1 are determined by their adjacency spectra except for four graphs.Ma and Wen[4]considered the problem ofDLSabout all connected graphs with second largest Laplacian eigenvalue at most θ,where θ=3.2470 is the largest root of the equation μ3?5μ2+6μ?1=0.Li,Guo and Shiu[5]showed that graphs with second largest Laplacian eigenvalue at most 3 are determined by their Laplacian spectra.For the detailed background and some known results on this subject,we refer the readers to the excellent surveys[6-8]and the references therein.
In this paper,we prove that all connected graphs with exactly two Laplacian eigenvalues greater than two are determined by their Laplacian spectra.
1 Preliminaries
We first present some well known results which will play an important role throughout this paper.
Lemma 1[2]LetGandHbeL-cospectral graphs.Then
(i)GandHhave the same number of vertices;
(ii)GandHhave the same number of edges;
(iii)GandHhave the same number of spanning trees;
(iv)GandHhave the same number of components;
Theorem 1[9]LetH(p,q)(p≥1,q≥0)be a double star tree(see Fig 1).ThenH(p,q)is determined by its Laplacian spectrum.
Now we quote a theorem due to Zhang in[10]which characterizes all connected graphs with exactly two Laplacian eigenvalues great than two.
Theorem 2[10]A connected graphGhas exactly two Laplacian eigenvalues greater than two if and only ifGis one of the following graphs shown in Tables 1,2 and Fig 1.

Table 1 Graphs with order n=3,4,5

Fig 1 Graphs H(p,q),F(p,q,m),Q(p,q,m)
Remark 1By Lemma 1(v),the graphsGin Tables 1 and 2 are not L-cospectral except forOn the other hand,by a direct calculation,
SpecL()=[4.3028,2.6180,2,0.6972,0.3820,0];SpecL()=[4.2143,3,1.4608,1,0.3249,0];
SpecL()=[4.5616,3,2,2,0.4384,0];SpecL()=[4.3028,3.6180,2,1.3820,0.6972,0];
SpecL()=[4.3028,4.3028,2,0.6972,0.6972,0]and SpecL()=[5.2361,3,2,1,0.7639,0].
Thus all graphs in Tables 1 and 2 are not L-cospectral.Finally,we conclude that all graphs in Tables 1 and 2 areDLS.

Table 2 Graphs with order n=6
2 The Laplacian spectral characterization of F(p,q,m)and Q(p,q,m)
In this section,we will consider the Laplacian spectral characterization ofF(p,q,m)andQ(p,q,m).In the following,we first compute the Laplacian polynomial ofF(p,q,m)andQ(p,q,m)respectively,and then prove those graphs areDLS.Before proceeding,we need the following Lemma 2.
Lemma 2[11]LetGbe a connected graph withnvertices which consists of a subgraphH(with at least two vertices)andn?|V(H)|distinct pendent edges(not inH)attached to a vertexvinH.Then

Φ(Lv(H);x)denotes the principal submatrix ofL(H)obtained by deleting the row and column corresponding to the vertexv.
Lemma 3LetF(p,q,m)be a graph with ordern=p+q+m+2(see Fig 1).Then

where
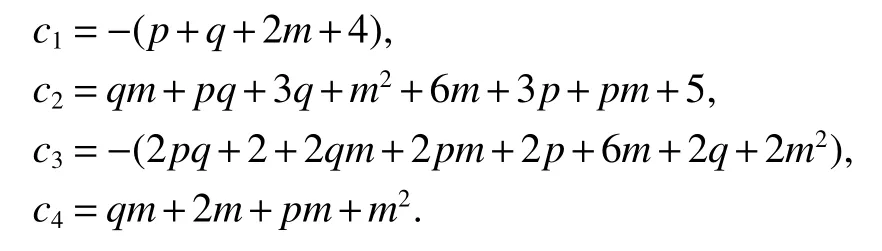
ProofLetHdenote the connected graph ofF(p,q,m)obtained by deleting thepandqdistinct pendent edges attached to a vertexuandvinF(p,q,m)(see Fig 1),respectively.Then

while

Thus by Lemma 2,

Substituting(1)and(2)into(3),we obtain

whereGdenotes the connected graph withm+2+qvertices ofF(p,q,m)obtained by deleting thepdistinct pendent edges attached to a vertexuinF(p,q,m).Also from Lemma 2,we obtain
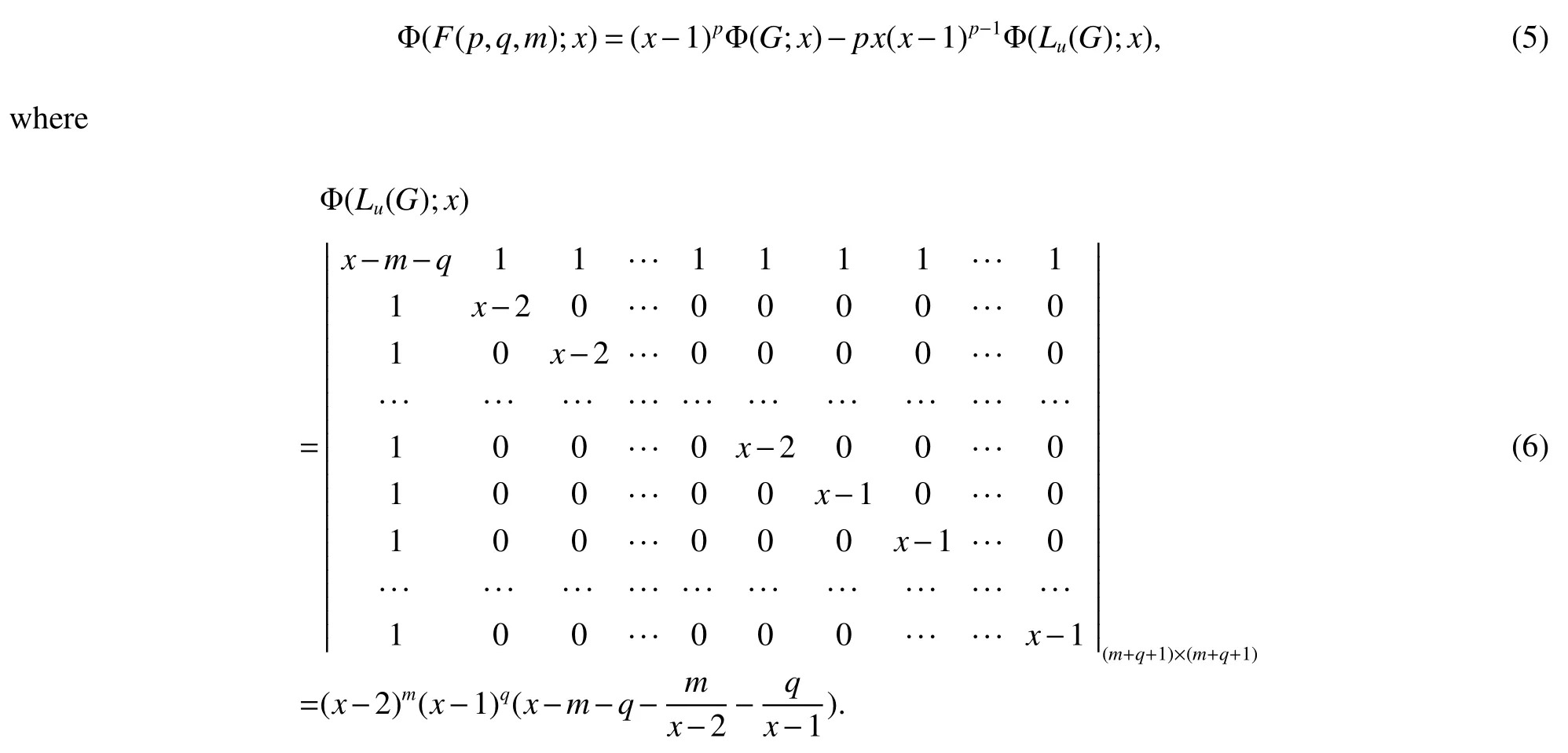
Substituting(4)and(6)into(5),thus we obtain
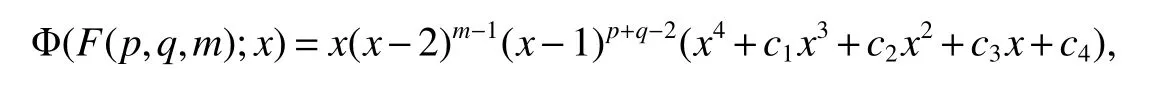
where
c1=?(p+q+2m+4),
c2=qm+pq+3q+m2+6m+3p+pm+5,
c3=?(2pq+2+2qm+2pm+2p+6m+2q+2m2),
c4=qm+2m+pm+m2.
By similar arguments,it is not difficult to obtain that the Laplacian polynomial ofQ(p,q,m)as the following lemma.
Lemma 4LetQ(p,q,m)be a graph with ordern=p+q+m+2(see Fig 1).Then

where
d1=?(p+q+2m+6),
d2=m2+pm+qm+8m+4p+4q+pq+13,
d3=?(2m2+2qm+2pm+10m+5p+5q+2pq+12),
d4=qm+4m+pm+m2+2p+2q+4.
Obviously,the graphF(p,q,m)andQ(p,q,m)(see Fig 1)are not L-cospectral by the Lemmas 3 and 4.
Theorem 3The graphF(p,q,m)(p≥0,q≥0,m≥1 andp+q+m≥5)displayed in Fig 1 is determined by its Laplacian spectrum.
ProofForF(p,q,m)withn≥7,if there exists a graphHwhich is L-cospectral withF(p,q,m).Then from Theorem 2,we haveHmay beH(p0,q0),F(p0,q0,m0)orQ(p0,q0,m0).Note thatH(p0,q0)is not L-cospectral withF(p,q,m)by Theorem 2.ThusHmay beF(p0,q0,m0)orQ(p0,q0,m0).From Lemmas 3 and 4,we may writeH=F(p0,q0,m0).Moreover,it is well known that the number of edges(or vertices)of a graph can be determined by its L-spectrum by Lemma 1.Then by Lemma 3 we have

In addition,from Eq.(8),we have
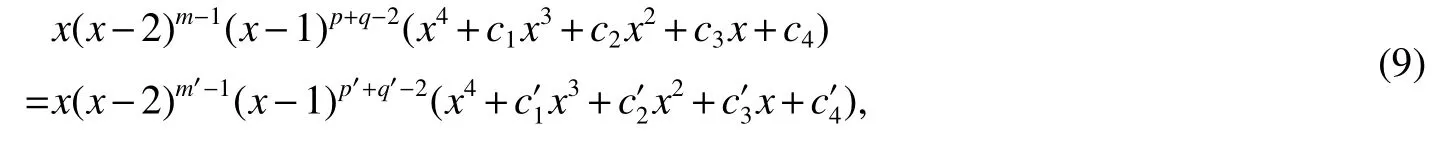
where
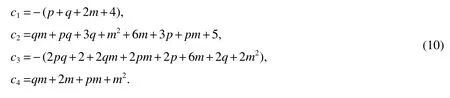
And
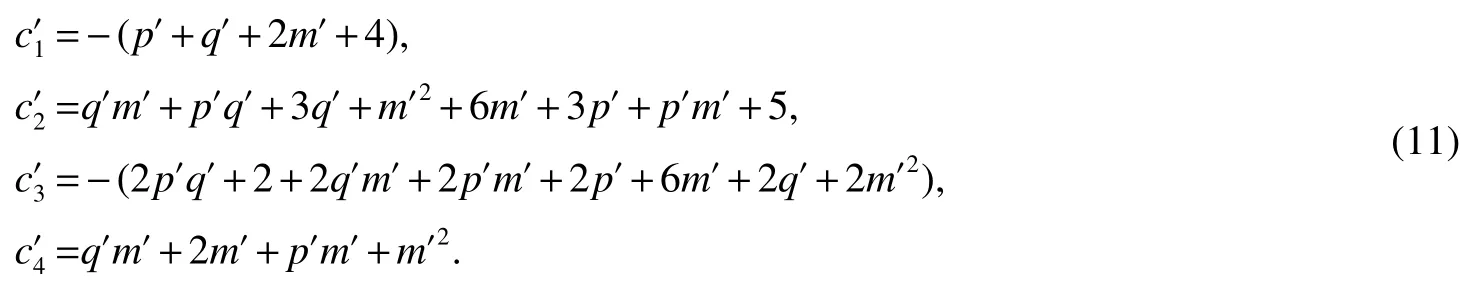
By Eq.(9),we get

Clearly,the left term in above Equation with the largest exponent isx4,and similarly for the right.So Eq.(12)impliesThat isp=p0andq=q0.Therefore,F(p,q,m)=F(p0,q0,m0)withn≥7.SoF(p,q,m)is determined by its Laplacian spectrum.We complete this proof.
By similar arguments,we have the following Theorem for graphQ(p,q,m).
Theorem 4The graphQ(p,q,m)(p≥0,q≥0,m≥1 andp+q+m≥5)displayed in Fig 1 is determined by its Laplacian spectrum.
Combining the results in Section 1 with the Theorems 3 and 4 in Section 2,we obtain:
Theorem 5All connected graphs with exactly two Laplacian eigenvalues greater than two are determined by their Laplacian spectra.
 新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2016年1期
新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)2016年1期
- 新疆大學(xué)學(xué)報(bào)(自然科學(xué)版)(中英文)的其它文章
- On the Page Number of Lexicographic Product of Paths and Cycles in Books?
- Community Diversity and its Seasonal Dynamics of Soil Mites in Oasis of the Sangong River Watershed of Xinjiang,China?
- 新疆伊犁鐵列克特金礦床流體包裹體特征分析?
- 工業(yè)企業(yè)規(guī)模、分布與區(qū)域經(jīng)濟(jì)增長(zhǎng)?
- Hartman-Wintner Theorem on the Noncommutative Hardy Spaces?
- 具有隨機(jī)干擾的單種群間歇擴(kuò)散模型?
