一類分數(shù)階復雜網(wǎng)絡混沌系統(tǒng)的投影同步*
毛北行 李慶賓
(鄭州航空工業(yè)管理學院理學院, 鄭州 450015)
?
一類分數(shù)階復雜網(wǎng)絡混沌系統(tǒng)的投影同步*
毛北行?李慶賓
(鄭州航空工業(yè)管理學院理學院, 鄭州450015)
根據(jù)分數(shù)階系統(tǒng)的相關理論研究了一類分數(shù)階復雜網(wǎng)絡混沌系統(tǒng)的投影同步問題,給出了分數(shù)階復雜網(wǎng)絡以及分數(shù)階時滯復雜網(wǎng)絡系統(tǒng)實現(xiàn)投影同步的充分性條件,仿真結(jié)果表明了方法的正確性.
投影同步,分數(shù)階系統(tǒng),復雜網(wǎng)絡
引言
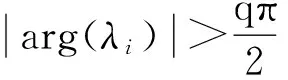
定義1[14]:Caputo分數(shù)階導數(shù)定義為:
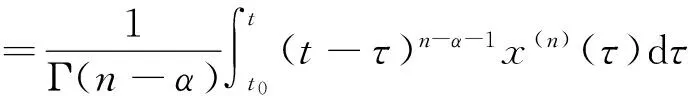
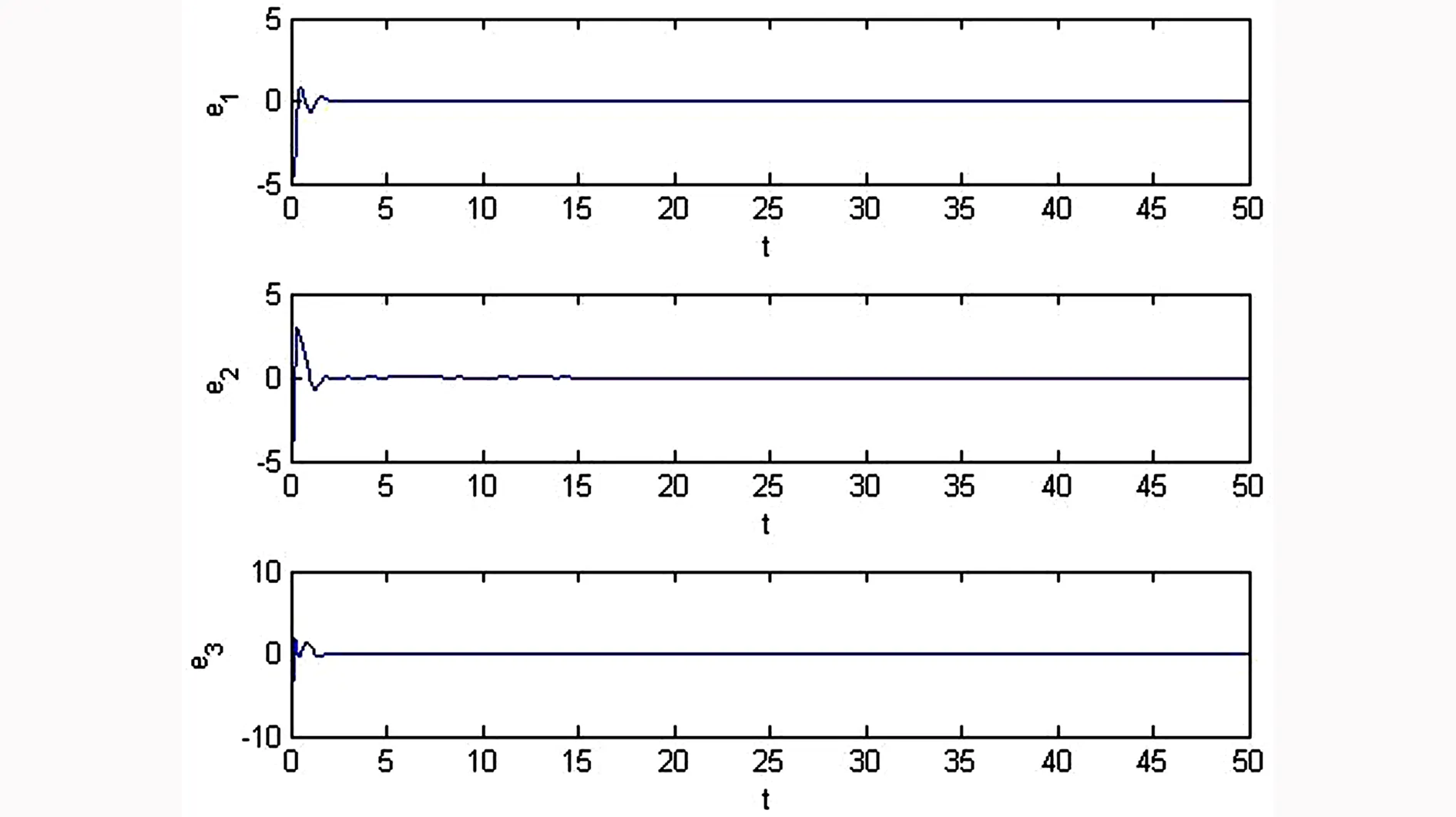
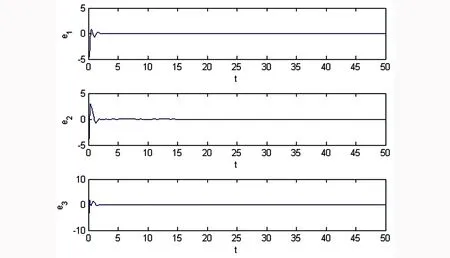
n-1<α 考慮如下一類分數(shù)階復雜網(wǎng)絡系統(tǒng): ui(t)(i=1,2,…,N), (1) A為適當維數(shù)的常數(shù)矩陣,ui為控制輸入,Γ是網(wǎng)絡的內(nèi)部耦合矩陣,C=(cij)N×N是外部耦合矩陣,滿足cij=0,(i≠j),cij≥0(i≠j),對角線元素定義為: (2) 假設1:復雜網(wǎng)絡的孤立節(jié)點的解滿足: Dtqs(t)=As(t)+f(s(t)) (3) s(t)可以是一個穩(wěn)定點,或者周期解,也可以是混沌軌跡. 定義1: 對給定的分數(shù)階系統(tǒng)(1),若存在一個非零矩陣Λ,使得 假設2:非線性函數(shù)滿足條件: ‖f(xi(t))-Λf(s(t))‖≤li‖xi(t)-Λs(t)‖,其中l(wèi)i為大于零的常數(shù). 定義系統(tǒng)誤差為: ei(t)=xi(t)-Λs(t), (i=1,2,…,N), 則有: Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ 引理1[15]:對于一般的分數(shù)階自治非線性微分方程Dtαx(t)=f(x(t)),當系統(tǒng)的階數(shù)0<α≤1時,如果存在實對稱正定矩陣P,使得J(x(t))=xT(t)PDtαx(t)<0,則上述分數(shù)階系統(tǒng)漸近穩(wěn)定. 定理1:設計控制器ui(t)=-kiei(t),若滿足條件(A+(li-ki)IN)+C?Γ<0則分數(shù)階復雜網(wǎng)絡系統(tǒng)(1)可以實現(xiàn)投影同步. 證明:由 Dtqei(t)=Aei(t)+f(xi(t))-Λf(s(t))+ C?Γ]ei(t)<0, 根據(jù)引理1,很容易得到定理1. 考慮如下一類分數(shù)階時滯復雜網(wǎng)絡系統(tǒng): Dtqxi(t)=Axi(t)+f(xi(t-τ))+ (i=1,2,…,N), (5) A為適當維數(shù)的常數(shù)矩陣,ui為控制輸入,τ為時滯常數(shù),Γ是網(wǎng)絡的內(nèi)部耦合矩陣,C=(cij)N×N是外部耦合矩陣,滿足cij≥0(i≠j),同時對角線元素定義為: (6) 假設3:復雜網(wǎng)絡的孤立節(jié)點的解滿足: Dtqs(t)=As(t)+f(s(t-τ)) (7) s(t)可以是一個穩(wěn)定點,或者周期解,也可以是混沌軌跡. 假設4:非線性函數(shù)滿足條件: ‖f(xi(t-τ))-Λf(s(t-τ))‖≤ li‖xi(t-τ)-Λs(t-τ)‖ 定義系統(tǒng)誤差為: ei(t)=xi(t)-Λs(t),(i=1,2,…,N), 則有: Dtqei(t)=Aei(t)+f(xi(t-τ))-Λf(s(t-τ))+ (8) 引理2[16]:分數(shù)階時滯系統(tǒng) Dtαx(t)=f(x(t),x(t-τ)),如果有正定的矩陣P和半正定矩陣Q滿足 xT(t)PDtαx(t)+xTQx(t)- xT(t-τ)Qx(t-τ)≤0, 則上述分數(shù)階時滯系統(tǒng)是Lyapunov穩(wěn)定的. 定理2:設計控制器ui(t)=-kiei(t),若滿足如下矩陣不等式(9),則分數(shù)階復雜網(wǎng)絡系統(tǒng)(5)可以實現(xiàn)投影同步. (9) 證明:根據(jù)引理2: 其中 e(t-τ)=[‖e1(t-τ)‖,‖e2(t-τ)‖,…, ‖eN(t-τ)‖]T. 選取分數(shù)階Lorenz系統(tǒng)為例,系統(tǒng)描述為 Dtqx1=a(x2-x1) Dtqx2=bx1-x1x3-x2 Dtqx3=x1x2-cx3, Dtqs1=a(s2-s1) Dtqs2=bs1-s1s3-s2 Dtqs3=s1s2-cs3 其中x1,x2,x3為狀態(tài)變量,a,b,c為系統(tǒng)參數(shù),當q=0.93,a=10,b=28,c=8/3時系統(tǒng)處于混沌狀態(tài).為了方便,取含三個節(jié)點的網(wǎng)絡進行仿真. 圖1 定理1中的系統(tǒng)誤差曲線Fig. 1 The system errors for Theorem 1 圖2 定理2中的系統(tǒng)誤差曲線Fig. 2 The system errors for Theorem 2 定理1中選取控制器ui(t)=-kiei(t),Λ=diag(-1,1,1),Γ=I3,li=1.2ki=1,從系統(tǒng)的誤差曲線如圖1所示, 定理2中選取控制器ui(t)=-kiei(t), Λ=diag(-1,1,1),Γ=I3,τ=0.5,li=1.5,ki=1.5,系統(tǒng)的誤差曲線如圖2所示. 研究了一類分數(shù)階復雜網(wǎng)絡混沌系統(tǒng)及其時滯系統(tǒng)的投影同步問題,基于Lyapunov穩(wěn)定性理論和分數(shù)階微積分的相關理論,給出了分數(shù)階復雜網(wǎng)絡以及分數(shù)階時滯復雜網(wǎng)絡實現(xiàn)投影同步的充分性條件,將系統(tǒng)實現(xiàn)投影同步的充分性條件轉(zhuǎn)化為矩陣不等式,從而更容易MATLAB求解,仿真結(jié)果表明了方法的正確性. 1徐爭輝,劉友金,譚文等.一個對稱分數(shù)階經(jīng)濟系統(tǒng)混沌特性分析.系統(tǒng)工程理論與實踐,2014,34(5):1237~1242 (Xu Z H, Liu Y J,Tan W,et al. Chaotic dynamics in a commensurate fractional-order nonlinear economic system.SystemsEngineeringandThroryPractice,2014,34(5):1237~1242 (in Chinese)) 2郝建紅,賓虹,姜蘇娜等.分數(shù)階線性系統(tǒng)穩(wěn)定理論在混沌同步中的簡單應用.河北師范大學學報自然版,2014,38(5):469~475 (Hao J H,Bin H,Jiang S N,et al. Stability theorem for fractional linear systems and its application in chaos synchronization.JournalofHebeiNormalUniversity(NaturalScuenceEdition),2014,38(5):469~475 (in Chinese)) 3鐘啟龍,邵永輝,鄭永愛.基于TS模型的分數(shù)階混沌系統(tǒng)同步.揚州大學學報(自然版),2012,17(2):46~49 ( Zhong Q L,Shao Y H,Zheng Y A. Synchronization of the fractional order chaotic systems based on TS models.JournalofYangzhouUniversity(NaturalScienceEdition),2012,17(2):46~49 (in Chinese)) 4張云雷,吳超然.基于反饋控制的分數(shù)階時滯神經(jīng)網(wǎng)絡的同步.重慶工商大學學報(自然版),2014,31(12):49~53(Zhang Y L ,Wu C R. Synchronization of fractional -order neural network with delay based on feedback control.JournalofChongqingTechnolBusinessUniversity(NaturalScienceEdition), 2014,31(12):49~53 (in Chinese)) 5韓敏,張雅美,張檬.具有雙重時滯的時變耦合復雜網(wǎng)絡的牽制外同步.物理學報,2015,64(7):5061~5069 (Han M,Zhang Y M,Zhang M. Outer syncronization analysis of two time-varying networks with double delays based on pinning control.ActaPhysicaSinica, 2015,64(7):5061~5069 (in Chinese)) 6Lü L, Li G,Guo Y. Generalized chaos synchronization of a weighted complex network with different nodes.ChinesePhysicsB,2010,19(8):5071~5077 7Mei J, Jiang M H, Wang J. Finite-time structure identification and synchronization of drive-response systems with uncertain parameter.CommunicationsinNonlinearScienceandNumericalSimulation,2013,(18):999~1015 8余明哲,張友安.一類不確定分數(shù)階混沌系統(tǒng)的滑模自適應同步.北京航空航天大學學報,2014,40(9):1276~1280 (Yu M Z, Zhang Y A. Sliding mode adaptive synchronization for a class of fractional-order chaotic systems with uncertainties.JournalofBeijingUniversityofAeronauticsandAstronautics, 2014,40(9):1276~1280 (in Chinese)) 9嚴勝利,張昭晗.一類不確定分數(shù)階混沌系統(tǒng)的同步控制.系統(tǒng)仿真技術(shù),2013,9(4):366~370 (Yan S L,Zhang Z H. Synchronization control of a class of uncertain fractional order chaotic systems.SystemSimulationTechnology, 2013,9(4):366~370 (in Chinese)) 10潘廣,魏靜.一種分數(shù)階混沌系統(tǒng)同步的只適應滑模控制器設計.物理學報,2015,64(4):5051~5057 (Pan G,Wei J. Design of an adaptive sliding mode controller for synchronization of fractional-order chaotic systems.ActaPhysicaSinica,2015,64(4):5051~5057 (in Chinese)) 11張燕蘭.分數(shù)階Rayleigh-Duffing-like系統(tǒng)的自適應追蹤廣義投影同步.動力學與控制學報,2014,12(4):348~352 (Zhang Y L. Adaptive tracking generalized projective synchronization of fractional Rayleigh-Duffing-like system.JournalofDynamicsandControl,2014,12(4):348~352 (in Chinese)) 12董俊,張廣軍,姚宏,王玨,許根.分數(shù)階異結(jié)構(gòu)超混沌系統(tǒng)完全同步與反相同步控制.動力學與控制報,2014,12(2):119~126 (D J, Z G J, Yao H, Wang J, Xu G. The control of complete synchronization and anti-phase synchronization for fractional-order hyper-chaotic systems of different structures.JournalofDynamicsandControl,2014,12(2):119~126 (in Chinese)) 13楊麗新,江俊.分數(shù)階復雜網(wǎng)絡系統(tǒng)的混合投影同步研究.動力學與控制學報,2015,13(1):52~55 (Yang L X,Jiang J. Hybrid projective synchronization of fractional-order complex dynamical networks.JournalofDynamicsandControl,2015,13(1):52~55 (in Chinese)) 14Podlubny. Fractional differential equation. Academic Press:San Diego,CA ,USA,1999 15胡建兵,趙靈冬.分數(shù)階系統(tǒng)穩(wěn)定性理論與控制研究.物理學報,2013,62(24):5041~5047 (Hu J B, Zhao L D. Stability theorem and control of fractional systems.ActaPhysicaSinica,2013,62(24):5041~5047 (in Chinese)) 16趙靈冬.分數(shù)階非線性時滯系統(tǒng)的穩(wěn)定性理論及控制研究[博士學位論文].上海:東華大學,2014 (Zhao L D. The stability theory of fracional nonlinear tiem-delay systems and its control[PhD Thesis]. Shanghai:Donghua University,2014 (in Chinese)) *The project supported by the National Natural Science Foundation of Tianyuan (11226337) ? Corresponding author E-mail: bxmao329@163.com 18 May 2015,revised 18 September 2015. PROJECTIVE SYNCHRONIZATION OF A CLASS OF FRACTIONAL-ORDER COMPLEX NETWORK CHAOS SYSTEMS* Mao Beixing?Li Qingbin (DepartmentofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China) The paper studied the projective synchronization problem of a class of fractional-order complex network chaos systems based on fractional order systems theory. The sufficient conditions for fractional-order complex network and its time-delayed systems to realize the projective synchronization was proposed. Numerical simulations of chaotic system verified the validity of the proposed method. projective synchronization,fractional order systems,complex networks E-mail: bxmao329@163.com 10.6052/1672-6553-2015-72 2015-05-18收到第1稿,2015-09-18收到修改稿. *國家自然科學基金數(shù)學天元基金資助項目(11226337)1 分數(shù)階復雜網(wǎng)絡系統(tǒng)的投影同步
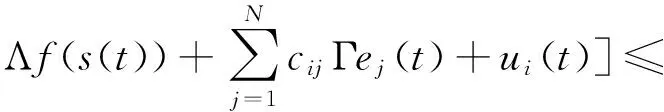
2 分數(shù)階時滯復雜網(wǎng)絡系統(tǒng)的投影同步
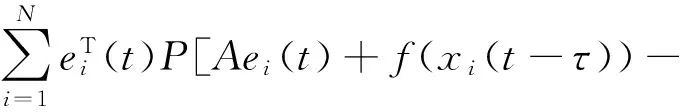
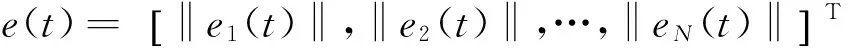
3 數(shù)值仿真
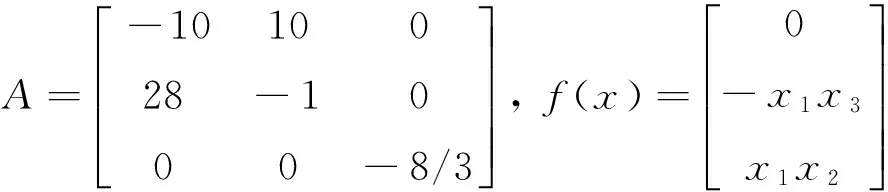
4 結(jié)論

