張海燕

(赤峰學院 數學與統(tǒng)計學院,內蒙古 赤峰 024001)

局部序列自同構

張海燕

(赤峰學院 數學與統(tǒng)計學院,內蒙古 赤峰 024001)

證明了維數大于等于3的可分Hilbert空間H上的所有有界線性算子全體B(H)的效應代數E(H)上滿的2-局部序列自同構是序列自同構以及Hilbert空間H上的投影算子全體P(H)上滿的2-局部序列自同構是序列自同構.

2-局部序列自同構; 序列自同構; 效應代數

0 引言

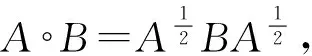
設映射φ:E(H)→E(H)是雙射,如果滿足φ(A°B)=φ(A)°φ(B),我們稱φ為序列自同構.利用上述運算,人們自然地可以研究效應代數上保這些運算的映射.Lajos Moln[1]證明了維數大于等于3的可分Hillbert空間H上的有界線性算子全體B(H)上的效應代數,簡記E(H),其上的序列自同構φ形如φ(A)=UAU*的形式,其中U為酉算子或反酉算子.本文在此基礎上研究了效應代數E(H)上的2-局部序列自同構的情況.并證明了E(H)上滿的2-局部序列自同構是序列自同構以及Hilbert空間H上的投影算子全體P(H)上滿的2-局部序列自同構是序列自同構.

1 主要結論

首先我們給出2-局部序列自同構的定義,設M=E(H) 或P(H),P(H)表示B(H)中投影算子的全體.設φ:M→M的映射,如果對于任意P,Q∈M,都存在M的一個序列自同構φP,Q,使得φP,Q(P)=φ(P),φP,Q(Q)=φ(Q).我們則稱φ為2-局部序列自同構.

引理1[2]設P∈E(H),若P是投影,則當且僅當P°P=P;P,Q是投影,若P≤Q,則當且僅當Q°P=P.

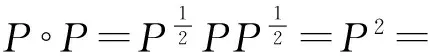
定理2 設φ:為P(H)→P(H)上滿的2-局部序列自同構,則φ是P(H)→P(H)上的序列自同構.

證明首先證明φ是單射.如果φ(P)=φ(Q),則存在P(H)的序列自同構φP,Q,使得,φP,Q(P)=φ(P),φP,Q(Q)=φ(Q),因此φP,Q(P)=φP,Q(Q).又因為φP,Q是單射,所以P=Q.因此φ是單射.

下面證明φ保投影.如果P是投影,則P°P=P,因為φ是2-局部序列自同構,所以存在P(H)的一個序列自同構φP,P使得φP,P(P)=φ(P).因此有φ(P)°φ(P)=φP,P(P)°φP,P(P)=φP,P(P°P)=φP,P(P)=φ(P),即φ(P)是投影.反之,如果φ(P)°φ(P)=φ(P),則φ(P)°φ(P)=φP,P(P)°φP,P(P)=φP,P(P°P)=φP,P(P)因為φP,P是單射,所以P°P=P.因此φ保投影.

下證φ對投影雙邊保序.如果P≤Q,則Q°P=P,又存在P(H)的一個序列自同構φP,Q,使得,φP,Q(P)=φ(P)φP,Q(Q)=φ(Q).所以φ(Q)°φ(P)=φP,Q(Q)°φP,Q(P)=φP,Q(Q°P)=φP,Q(P)=φ(P),由引理1知,φ(P)≤φ(Q).反之如果φ(P)≤φ(Q),則φ(Q)°φ(P)=φ(P).又存在P(H)的一個序列自同構φP,Q,使得

φ(Q)°φ(P)=φP,Q(Q)°φP,Q(P)=φP,Q(Q°P)=φ(P)=φP,Q(P),

即φP,Q(Q°P)=φP,Q(P).

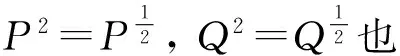
綜上證明可知φ又是單射和滿射,因此φ為P(H)→P(H)上的序列自同構.

定理3 設φ:E(H)→E(H)是滿的2-局部序列自同構,則φ是E(H)→E(H)的序列自同構.

證明我們先證φ是單射.如果φ(A)=φ(B),A,B∈E(H).則存在E(H)上的序列自同構φA,B使得,φA,B(A)=φ(A),φA,B(B)=φ(B).因此可得φA,B(A)=φA,B(B).又因為φA,B是單射,所以A=B.因此φ是單射.且易證φ(I)=I.對于任意A,B∈E(H).則ABA∈E(H).由中推論[4]可知,對于任意A∈E(H).有φ(A)=UAU*,其中U是酉算子或反酉算子.因此可得φ(ABA)=UABAU*.又因為φ是2-局部序列自同構,則存在序列自同構φA,B使得,

φA,B(A)=φ(A),φA,B(B)=φ(B).

進一步可得

φ(ABA)=UABAU*=UAU*UBU*UAU*=φ(A)φ(B)φ(A).

因此有

綜上證明可知φ又是單射和滿射,因此φ是φ:E(H)→E(H)上的序列自同構.

[3]Stan Gudder,Richard Greechie.Uniqueness and order in sequential effect algebras[J].International Journal of the oretical physics,2005,44(7):755-770.

[4]張海燕.2-局部序列自同構[J].赤峰學院學報,2011,27(6),20-21.

[責任編輯：李春紅]

LocalSequentlalAutomorphisms

ZHANG Hai-yan

(School of Mathematics and Statistics,Chifeng College,Chifeng Inner Mongolia 024001,China)

In this paper,It was proved that every surjective two-local sequential automorphism on effect algebrasE(H) ofB(H) which denoted all the bounded linear operators on separable Hilbert spaceHis sequential automorphism,If dimHis equal or more three.and prove that each surjective two-local sequential automorphism onP(H) which denoted all the projections on separable Hilbert spaceHis sequential automorphism.

two-local sequential automorphism; sequential automorphism; effect algebra

2014-11-04

張海燕(1981-),女,吉林長春人,講師,碩士,研究方向為泛函分析.E-mail:12300741@qq.com

O177.1

:A

:1671-6876(2015)01-0021-03