Numerical simulation of effects of operating conditions on the molecular weight of polypropylene using a response surface method
HONG Dong-feng(洪東峰), SUI Shu-hui(隋述會(huì)), WU Wen-hui(吳文輝)
(School of Materials Science and Engineering, Beijing Institute of Technology, Beijing 100081, China)
?
Numerical simulation of effects of operating conditions on the molecular weight of polypropylene using a response surface method
HONG Dong-feng(洪東峰), SUI Shu-hui(隋述會(huì)), WU Wen-hui(吳文輝)
(School of Materials Science and Engineering, Beijing Institute of Technology, Beijing 100081, China)
A L4635Box-Behnken design was used for developing a model to predict and optimize the molecular weight (Mw) of polypropylene (PP); a second-order polynomial regression equation was derived to predict responses. The significance of variables and their interactions were tested by means of the ANOVA with 95% confidence limits; the standardized effects were investigated by Pareto chart, the optimum values of the selected variables were obtained by analyzing the response surface contour plots. The optimizedMwvalue of 1.217×105g/mol was very close to the industrial value ((1.22±0.004)×105g/mol) at the optimum values.
molecular weight (Mw); propylene polymerization; Box-Behnken design (BBD); optimization modeling; loop reactor
Nowadays, the requirement of product properties of the PP are increasing continuously, and the properties of PP were significantly affected by their molecular weight (Mw) or melt flow rate (MFR). There were many methods to predictMwor MFR[1-2]. In case of a limited removal of H2, molecular weight distribution (MWD) can be widen limitedly, and the forced removal of H2could potentially double the polydispersity index (PDI) of PP[1]. A comprehensive mathematical model using the method of moments was developed to simulate the dynamic behavior of an industrial slurry-phase olefin multi-sites Z-N catalytic polymerization loop reactor[2]. These methods were able to simulate the dynamic operation of an industrial PP loop reactor. However, these methods only considered the effect of one single factor on theMwof PP, but polymerization of PP is very complex, when multi-factors (i.e.,T,P, mass flow, etc.) affect theMwsimultaneously, and/or there exist a response action, these methods seem to have some limitations.
To investigate multi-factor’s effect to theMwof PP and their response action, and to predict the real-timeMw, Box-Behnken design (BBD) combined with response surface modeling (RSM)[3]is used for studying the effect of multi-factor’s influence on theMwof PP by varying the factors simultaneously. In this work, we analyzed the ASPEN simulation results by the RSM for the first time, and obtained an equation including multi-factor’s interplay, as well as 3D surfaces. The response surface can be explored to determine important characteristics when there are multiple responses[4].
RSM is to optimize the response surface that is influenced by various process parameters, andalso to quantify the relationship between the controllable input parameters and the obtained response surfaces[5]. A method to the BBD algorithm provides the design-expert, and a combinatorial approach for multi-parameter problems, such as the effect of operating conditions on theMwof PP. This methodology was developed mainly for quality control and process optimization[6].
The main objectives of this study were: firstly, to investigate the effects of selected operational variables viz. polymerization temperature (T, ℃), polymerization pressure (P, MPa), mass flow of propylene (qP, t/h), mass flow of catalyst (qC, kg/h), and volume fraction of hydrogen (φH, 10-4%) onMwof PP, and secondly to develop a quadratic model for prediction and optimization ofMwof PP. Accordingly, BBD-based simulations were carried out in ASPEN Plus.
1 Method and analysis
1.1 RSM modeling forMwof PP
BBD was found to be a suitable designs to minimize the number of tests while obtain the highest correlation between the observed data and predicted values. In all, 46 (L4635) batch simulations were conducted by Aspen Plus, instead of having 243 experimental points if the run was done in 35complete factorial design[7]. Consequently, the research was determined by a L4635BBD combining with RSM and quadratic programming (QP)[8]. In the step of RSM, a suitable approximation was introduced to find true relationship between the response and the factors, then, the behavior of the system was expressed by the following quadratic equation[8-9]:
(1)
whereyis the process response,nis the number of the patterns,iandjare the index numbers for pattern,a0is the intercept term,x1,x2, …,xnare the independent variables,ai,aiiandaijare the linear, quadratic and interaction effect respectively, andεis the random error.
In this study, the effects ofT,P,qP,qC, andφHwere investigated. Each independent variables was consecutively coded asx1,x2, …,x5at three levels. The experimental range and levels of independent variables are presented in Tab.1.

Tab.1 Experimental range and levels of independent variables
1.2 Simulation of propylene polymerization with Aspen Plus
Based on propylene polymerization mechanism which catalyzed by Z-N catalyst and its corresponding rate constants, simulate the industry-scale propylene polymerization process by Aspen Plus, and search the impact of operating conditions on theMwof PP. Aspen Plus is a process modeling software that is widely used in a variety of steady state or dynamic modeling applications[10-11]. In this paper, PC-SAFT equation of state is used as property method.
1.3 Optimization of theMwof PP by RSM
The adequacy of the quadratic model and statistical significance of the regression coefficients were tested by ANOVA and the student’sttest statistics. The observed and the model-predicted values of the response variable (Mw) were used to compute correlation coefficient (R), root mean square error (RMSE), and relative standard error (RSE). The RMSE and RSE values may be used to evaluate the predictive ability of the selected model. RMSE and RSE are measure of the goodness of fit[9]; best describe an average measure of the error in predicting the dependent variable by the selected model. These analyses were performed with SPSS Statistics.
1.4 Statistical analysis

2 Result and discussion
2.1 Determination of the model
By applying multiple regression analysis on the design matrix and the responses, a quadratic model was selected for developing the mathematical relationship between the response and the condition variables of PP polymerization. Based on the requirements of product performance, theMwof PP was 1.22×105g/mol. Quadratic regression modeling was performed between the response variable (Mw) and the corresponding values (T,P,qP,qC, andφH) of the five different variables, the following quadratic equation was established to explain theMwof PP:
Mw=12.284-4.385×10-4T2-0.848P2-
0.375T+2.265P+91.63qC-5.284qP+9.544×
10-2φH-0.726TP+0.112TqC+0.239TqP+4.778×10-2PφH-22.66qCqP-0.778qCφH
(2)
whereMwis the predictedMw. The optimum values of the selected test variables were obtained by solving Eq.(2). It is essential to analyze the variance to test the significance of the model[8], therefore, the ANOVA was conducted to test the significance of the fit of the quadratic equation for the experimental data as presented in Tab.2.

Tab.2 Determination of the regression model and statistical evaluation
The ANOVA of the regression model (Eq. (2)) showed that the quadratic model was highly significant, which was evident from theF-Value with a very lowp-value. The goodness of fit of the model was checked by theR2between the observed and predicted values of the response variable (Fig.1). The points cluster around the diagonal line indicates a good fit of the model, since the deviation between the observed and predicted values was very small[12]. A plot of normal probability of the residuals is depicted in Fig.2 to de-tect and explain the systematic departures from
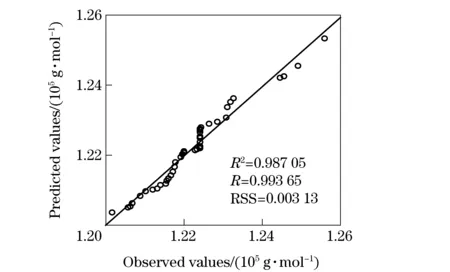
Fig.1 Plot of the observed and predicted values of the response variable
the assumptions, where the normal probability of residuals displays a satisfactory normal distribution, confirming the normality assumptions made earlier and the independence of the residuals[13]. All the other detections mentioned in Tab.2 shown that the regression model was sufficient to describe the effects of the operating conditions on theMwof PP.

Fig.2 Normal probability of the raw residuals
2.2 Effects of model components and their interactions onMwof PP
The standardized effects of the independent variables and their interactions on the dependent variable were investigated by a Pareto chart[9](Fig.3). The significance order of process variables is as follows:φH>qP>qC>P?T,φHhad the highest level of significance with a contribution of 49.85%, and first-order terms had the highest level of significance with a total contribution of 60.86%, this shown the model had some linear relationship to a certain extent.

SE-Standardized effect; TPC-Total percentage contributions; CE-Cumulative effectFig.3 Pareto chart and a detailed schematic
2.3 3D response surfaces plots of the relationship betweenMwand condition parameters
The regression model has five independent variables. Fig.4 shows the 3D response surfaces as the functions of two variables at the center level of other variables. The nonlinear nature of all 3D response surfaces demonstrated that there were considerable interactions between each independent variables and theMwof PP.

Fig.4 3D response surface diagrams of the impact of different factors on the Mw
Fig.4 shows that theMwof PP increased with the increase ofqP, and reduced with the increase ofT. For a givenMw=1.226 5×105g/mol appears inT=69.95 ℃,qP=7.08 t/h; asφHchanged, theMwchanged with a quadratic curve at the extreme ofφH=1.3×10-4% approximately. Meanwhile, with the increase ofP, theMwchanged slightly. WhenP=3.357 MPa,φH=1.24×10-4%,Mwwould reach the optimal value of 1.228 8×105g/mol; theMwof PP changed in the parabolic behavior with the increase inφH, and changed approximately linearly with the increase inqC. The optimal valueMw=1.225 5×105g/mol appears inφH=0.19,qC=0.19 kg/h. Whereas, the effects ofT,P,qP, andqConMware not significantly asφHdoes. These trends indicate that the catalyst displays a high hydrogen response.
2.4 Validation of the regression model
Optimization modeling use the developed quadratic model to assess the appropriateMw, and the quadratic prediction model was validated by the statistical analysis. The results indicated that theMwobtained from the model response (1.217×105g/mol) was in good agreement with that of the industrial value ((1.22±0.004)×105g/mol). From the engineering point of view, the proposed model to describe theMwof PP was also validated by means of various descriptive statistics considered in this work.
3 Conclusion
The L4635BBD combined with RSM and QP was used for optimizing theMwof PP produced by the loop reactor. The proposed model also provided a critical analysis of the simultaneous interactive effects of independent variables, viz.,T,P,qP,qCandφH. The regression model was detected by ANOVA,χ2test, etc. All the detections shown that the quadratic regression model is sufficient to describe the effects of the operating conditions on theMwof PP. At the same time, there also has a certain liner characteristic in the model. The optimum process variables were:T=69.54 ℃,P=3.31 MPa,qP=7.08 t/h,qC=0.19 kg/h, andφH=1.24×10-4%, and with a predictedMwabout 1.217×104g/mol, which was clearly in good agreement with that of the industrial value ((1.22±0.004)×105g/mol). The model can be applied to predict theMwof the PP in real time according to the operating conditions, or adjust the operating conditions when theMwof PP deviates from the target value.
[1] Ali M A H, Stroomer J, Betlem B, et al. Molecular weight distribution broadening of polypropylene by periodic switching of hydrogen and catalyst additions[J]. Journal of Applied Polymer Science, 2008, 108(4): 2446-2457.
[2] Touloupides V, Kanellopoulos V, Pladis P, et al. Modeling and simulation of an industrial slurry-phase catalytic olefin polymerization reactor series[J]. Chemical Engineering Science, 2010, 65(10): 3208-3222.
[3] Box G E P, Wilson K B. On the experimental attainment of optimum conditions[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1951, 13(1): 1-45.
[4] Mason R L, Gunst R F, Hess J L. Statistical design and analysis of experiments[M]. Hoboken: John Wiley & Sons Inc, 2003.
[5] Gunaraj V, Murugan N. Application of response surface methodology for predicting weld bead quality in submerged arc welding of pipes[J]. Journal of Materials Processing Technology, 1999, 88(1-3): 266-275.
[6] Leardi R. Experimental design in chemistry: A tutorial[J]. Analytica Chimica Acta, 2009, 652(1-2): 161-172.
[7] Negi L M, Jaggi M, Talegaonkar S. A logical approach to optimize the nanostructured lipid carrier system of irinotecan: efficient hybrid design methodology[J]. Nanotechnology, 2013, 24(1): 015104.
[8] Can M Y, Kaya Y, Algur O F. Response surface optimization of the removal of nickel from aqueous solution by cone biomass of Pinus sylvestris[J]. Bioresource Technology, 2006, 97(14): 1761-1765.
[9] Singh K P, Rai P, Pandey P, et al. Modeling and optimization of trihalomethanes formation potential of surface water (a drinking water source) using Box-Behnken design[J]. Environmental Science and Pollution Research, 2012, 19(1): 113-127.
[10] Sadeghifar H, Sadeghifar A. A new method to calculate efficiency of randomly-packed distillation columns and its comparison with the methods utilized in ASPEN Plus[J]. Fuel Processing Technology, 2012, 96: 65-73.
[11] Yi Qun, Feng Jie, Li Wenying. Optimization and efficiency analysis of polygeneration system with coke-oven gas and coal gasified gas by Aspen Plus[J]. Fuel, 2012, 96(1): 131-140.
[12] Imandi S B, Bandaru V R, Somalanka S R,et al. Optimization of medium constituents for the production of citric acid from byproduct glycerol using Doehlert experimental design[J]. Enzyme and Microbial Technology, 2007, 40(5): 1367-1372.
[13] Liu Hsuanliang, Lan Yannwen, Cheng Yangchu. Optimal production of sulphuric acid by thiobacillus thiooxidans using response surface methodology[J]. Process Biochemistry, 2004, 39(12): 1953-1961.
(Edited by Cai Jianying)
10.15918/j.jbit1004- 0579.201524.0218
TQ 322.2 Document code: A Article ID: 1004- 0579(2015)02- 0254- 06
Received 2013- 08- 21
Supported by the R & D Program of Catalyst Company, SINOPEC (G8101-11-ZS-0016*)
E-mail: wuwh@bit.edu.cn
 Journal of Beijing Institute of Technology2015年2期
Journal of Beijing Institute of Technology2015年2期
- Journal of Beijing Institute of Technology的其它文章
- Nonlinear symbolic LFT model for UAV
- Novel scheme of high precision inertial measurement for high-speed rotating carriers
- Study on influencing factors of adapters separating with the underwater missile
- Fast-solving method for air-to-surface guided bombs’ allowable attack area
- Design and analysis of mechanical self-destruction and self-neutralization mechanism for submunition fuze
- Resilience approach for heterogeneous distributed networked unmanned weapon systems
