Iyd S.Alkroosh,Mohmmd Bhdori,Hmid Nikrz,Alirez Bhdori

aDepartment of Civil Engineering,College of Engineering,Al-Qadissiya University,Al Diwaniyah,Iraq

bSchoolof Soil Science and Engineering,University of Tehran,Tehran,Iran

dSchoolof Environment,Science and Engineering,Southern Cross University,Lismore,New South Wales,Australia

Full length article

Regressive approach for predicting bearing capacity of bored piles from cone penetration test data

Iyad S.Alkroosha,Mohammad Bahadorib,Hamid Nikrazc,Alireza Bahadorid,*

aDepartment of Civil Engineering,College of Engineering,Al-Qadissiya University,Al Diwaniyah,Iraq

bSchoolof Soil Science and Engineering,University of Tehran,Tehran,Iran

cDepartment of Civil Engineering,Curtin University,Perth,Australia

dSchoolof Environment,Science and Engineering,Southern Cross University,Lismore,New South Wales,Australia

A R T I C L E I N F O

Article history:

Received 27 April2015

Received in revised form

12 June 2015

Accepted 30 June 2015

Available online 5 August 2015

Bored piles Cone penetration test(CPT) Bearing capacity Least square support vector machine (LSSVM) Training Validation

In this study,the least square support vector machine(LSSVM)algorithm was applied to predicting the bearing capacity of bored piles embedded in sand and mixed soils.Pile geometry and cone penetration test(CPT)results were used as input variables for prediction of pile bearing capacity.The data used were collected from the existing literature and consisted of 50 case records.The application of LSSVM was carried out by dividing the data into three sets:a training set for learning the problem and obtaining a relationship between input variables and pile bearing capacity,and testing and validation sets for evaluation ofthe predictive and generalization ability of the obtained relationship.The predictions ofpile bearing capacity by LSSVM were evaluated by comparing with experimental data and with those by traditionalCPT-based methods and the gene expression programming(GEP)model.It was found that the LSSVMperforms wellwith coef fi cientofdetermination,mean,and standard deviation equivalent to 0.99, 1.03,and 0.08,respectively,for the testing set,and 1,1.04,and 0.11,respectively,for the validation set.The low values of the calculated mean squared error and mean absolute error indicated that the LSSVMwas accurate in predicting the pile bearing capacity.The results of comparison also showed that the proposed algorithm predicted the pile bearing capacity more accurately than the traditional methods including the GEP model.

?2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

1.Introduction

Bearing capacity is one of the most important factors that govern the design of pile foundations.Therefore,it has been the subject of interest for many researchers throughout the history of the geotechnical engineering profession.As a result,numerous theoretical and experimental procedures have been proposed to predict the pile behavior and bearing capacity.However,accurate evaluation ofpile bearing capacity and certain interpretation ofpile load transfer mechanism are still far from being accomplished due to the complexity of the problem.

The theoretical solutions,which employ the theory of bearing capacity to calculate the pile shaft and tip resistance,involve shortcomings resulting from considerable uncertainty over the factors that in fl uence the bearing capacity.Among those factors are the effect of installation method,stress history and soil compressibility.For bored piles embedded in layered soil,the problem is more complex due to sensitivity of the factors that affect the behavior of the pile and the dif fi culty in quantifying those factors. For instance,the friction angle between pile and the surrounding soil cannot be exactly determined because of the effect of installation procedure and the dif fi culty in fi nding the real soil properties.

The experimental solutions that correlate the results of in-situ tests such as standard penetration test(SPT)or cone penetration test(CPT)with pile bearing capacity also involve setbacks.That may be attributed to that the SPT has substantially inherent variability and does not re fl ect soil compressibility(Abu-Kiefa,1998).Moreover,the SPT results are affected by many factors,such as operator, drilling,hammer ef fi ciency,and rate of blows.Hence,the accuracy of the proposed correlations between SPT data and pile bearing capacity is not assured.Although the correlation between pile capacity and CPT data can be a better alternative to the SPT correlation,comparative studies of the available CPT-based methods carried out by a number of researchers(e.g.Briaud,1988;Roberston et al.,1988;Eslami,1997;Abu-Farsakh and Titi,2004;Cai et al., 2008)have shown that the capacity predictions can be verydifferent for the same case depending on the method employed.It is also found that these methods cannot provide consistent and accurate prediction of pile bearing capacity.

Considering the limitations of the proposed procedures for predicting pile bearing capacity and the limited success that they have achieved in terms of providing accurate prediction of pile bearing capacity,further research is required to overcome the complications associated with the problem.Arti fi cial intelligence techniques may be better alternatives,due to the capability ofbeing able to deal with complex and highly nonlinear functions,and employing the considerable capacity of computers to perform enormously iterated work.The modeling advantage of these techniques is their ability to capture the nonlinear and complex relationships between the targeted output and the factors affecting it, without having to assume a priori formula describing this relationship.A number of researchers(e.g.Teh et al.,1997;Abu-Kiefa, 1998;Das and Basudhar,2006;Ardalan et al.,2009;Shahin,201 Ornek et al.,2012;Tarawneh,2013)have successfully applie arti fi cial neural network(ANN),which is a form of arti fi cial inte ligence,to solving engineering problems.Genetic programmin (GP),which is another form of arti fi cialintelligence,has been use successfully in solving engineering problems(Rezania and Javad 2007;Alavi et al.,2011;Alkroosh and Nikraz,2011a,b;Gandom 2011;Gandomi and Alavi,2012).Recently,an emerging alg rithm,i.e.the least square support vector machine(LSSVM),which is a developed version of support vector machine(SVM),has been found successfulin solving engineering problems(Das et al.,2011a, b;Samui and Kothari,2011).This study investigates the feasibility of using the LSSVM to predict the bearing capacity of bored piles embedded in sand and mixed soils more accurately than the available methods.

2.Support vector machine(SVM)

The SVM is a method developed using the statistical learning concept(Suykens and Vandewalle,1999).It has been widely used across the world(Cortes and Vapnik,1995;Bazzani et al.,2001; Suykens et al.,2002;Amendolia et al.,2003;Baylar et al.,2009; übeyli,2010;Chen et al.,2011;Chamkalani et al.,2013;Ra fi ee-Taghanaki et al.,2013;Shokrollahi et al.,2013).

If we have training samples with given data xi∈Rnand result data yi∈R with labels-1 and 1,respectively,the SVMestimates the function shown below(Suykens and Vandewalle,1999;Suykens et al.,2002):

whereΦ（x）is the function that maps x,and w and b are the weight vector and bias variable.When the data are separable,we will have (Suykens and Vandewalle,1999;Suykens et al.,2002):

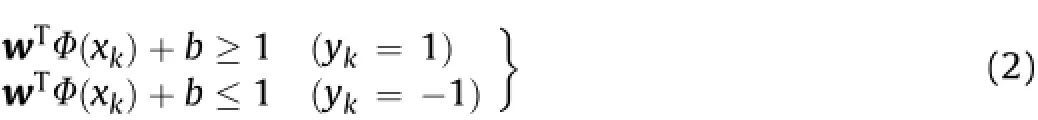
Eq.(2)is nearly equal to(Das et al.,2011a,b;Chamkalani et al., 2013):

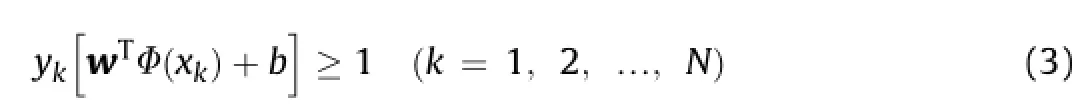
The further development of linear SVM to non-independent case was also created by Cortes and Vapnik(1995).Simply,it is done by presenting extra variables into Eq.(3)(Suykens and Vandewalle,1999;Suykens et al.,2002):

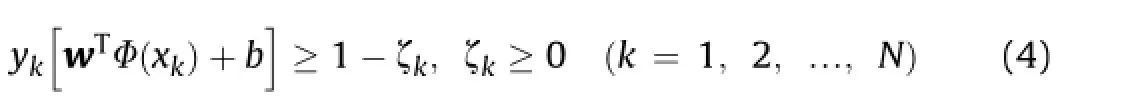
whereζkis the deviation factor.

The optimalseparating hyperplane is predicted using the vector w that minimizes the functional conditions using the constraints (Eq.(4))(Suykens and Vandewalle,1999;Suykens et al.,2002; übeyli,2010):

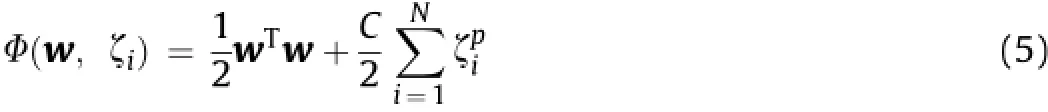
where p is the upper limit,and C is a coef fi cient.

In the SVM,optimal separating hyperplane is calculated using the quadratic method(Cortes and Vapnik,1995):

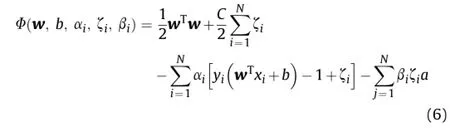
where a is the adjustable parameter,αiandβiare the Lagrange multipliers(Suykens and Vandewalle,1999;Suykens et al.,2002).

In contrast to the SVM,the LSSVM is developed using minimization of cost equation(Suykens and Vandewalle,1999;Suykens et al.,2002):

To derive the dual problem for the nonlinear classi fi cation problem of LSSVM,the Lagrange function is de fi ned as(Suykens and Vandewalle,1999;Suykens et al.,2002):

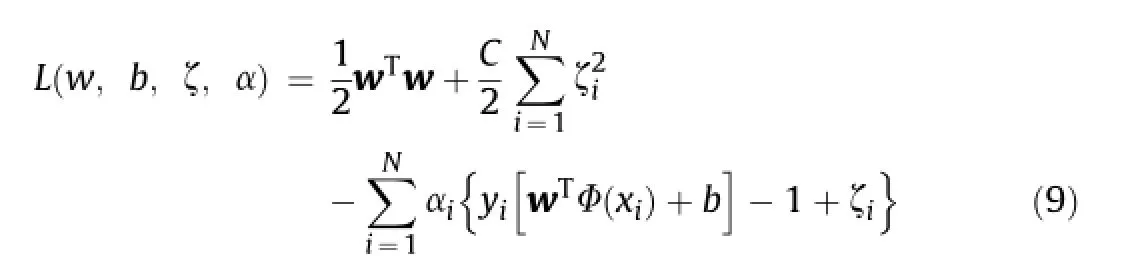
The conditions for optimality can be obtained as

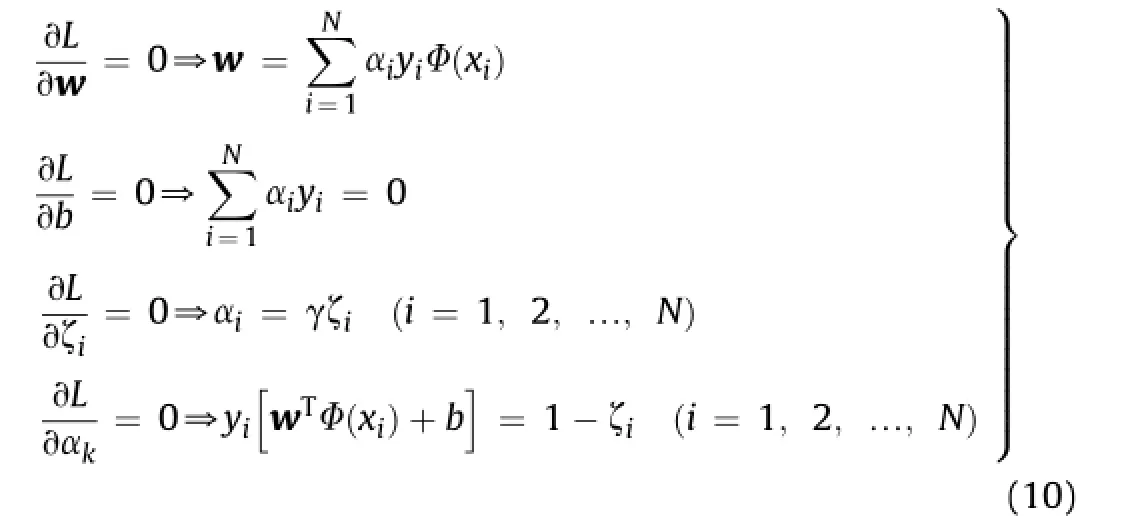
By de fi ning ZT=［ΦT（x1）y1,ΦT（x2）y2,…,ΦT（xN）yN］,Y=［y1,y2,…,yN］,［1,1,…,1］,ζ=［ζ1,ζ2,…,ζN］,α=［α1,α2,…,αN］,Eq.(10)is fi nally converted into the below form (Minoux,1986;Suykens and Vandewalle,1999):

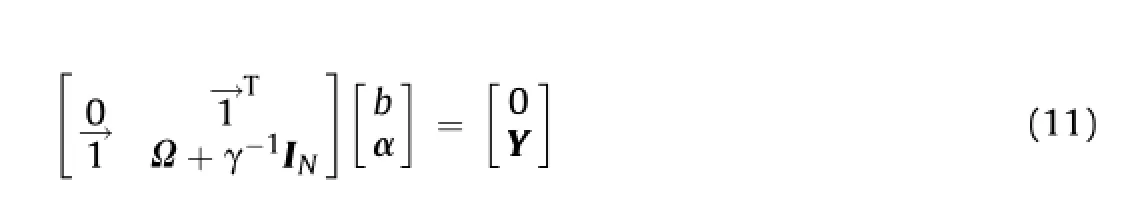
where INis an N×N identity matrix,andΩ∈RN×Nis the kernel matrix de fi ned by

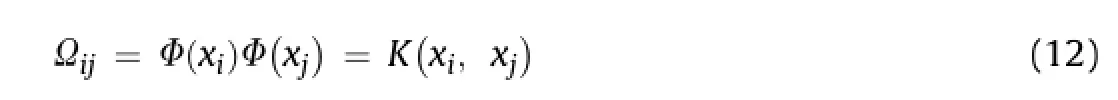
Most extensively used kernelfunctions are radialbasis function (RBF)(Eq.(13))and polynomial function(Eq.(14))(Gunn,1998; Müller et al.,2001):

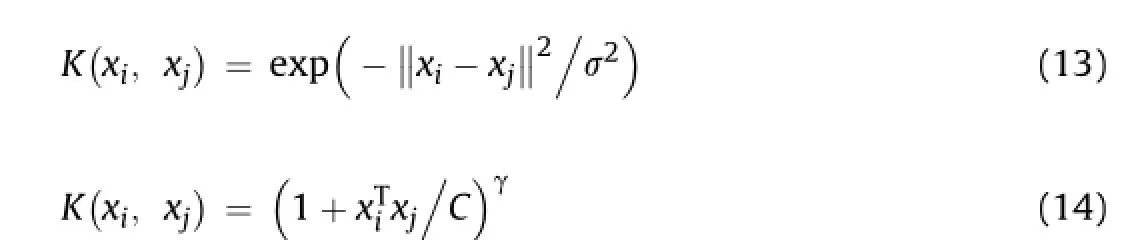
whereσis an independent variable.

This work uses the RBF(Baylar et al.,2009;Xavier-de-Souza et al.,2009;Deng and Yeh,2010;Chamkalani et al.,2013;Ra fi ee-Taghanaki et al.,2013;Shokrollahi et al., 2013)kernel,which is suitable for the LSSVM mathematical modeling.

3.Application of LSSVM for predicting pile bearing capacity

3.1.Database used

The application of LSSVM in this work is based on pile load test and CPT data,reported in Alsamman(1995),Eslami(1997)and Alkroosh and Nikraz(2011a,b).The case records were collected from a wide spectrum of geographic locations all over the world. Most of the piles embedded in layered soil of sand and clay.The piles were tested under slow maintained compression loads.According to Ng et al.(2004),the piles were classi fi ed into small diameter piles(diameter＜600 mm)and large diameter piles (diameter＞600 mm).

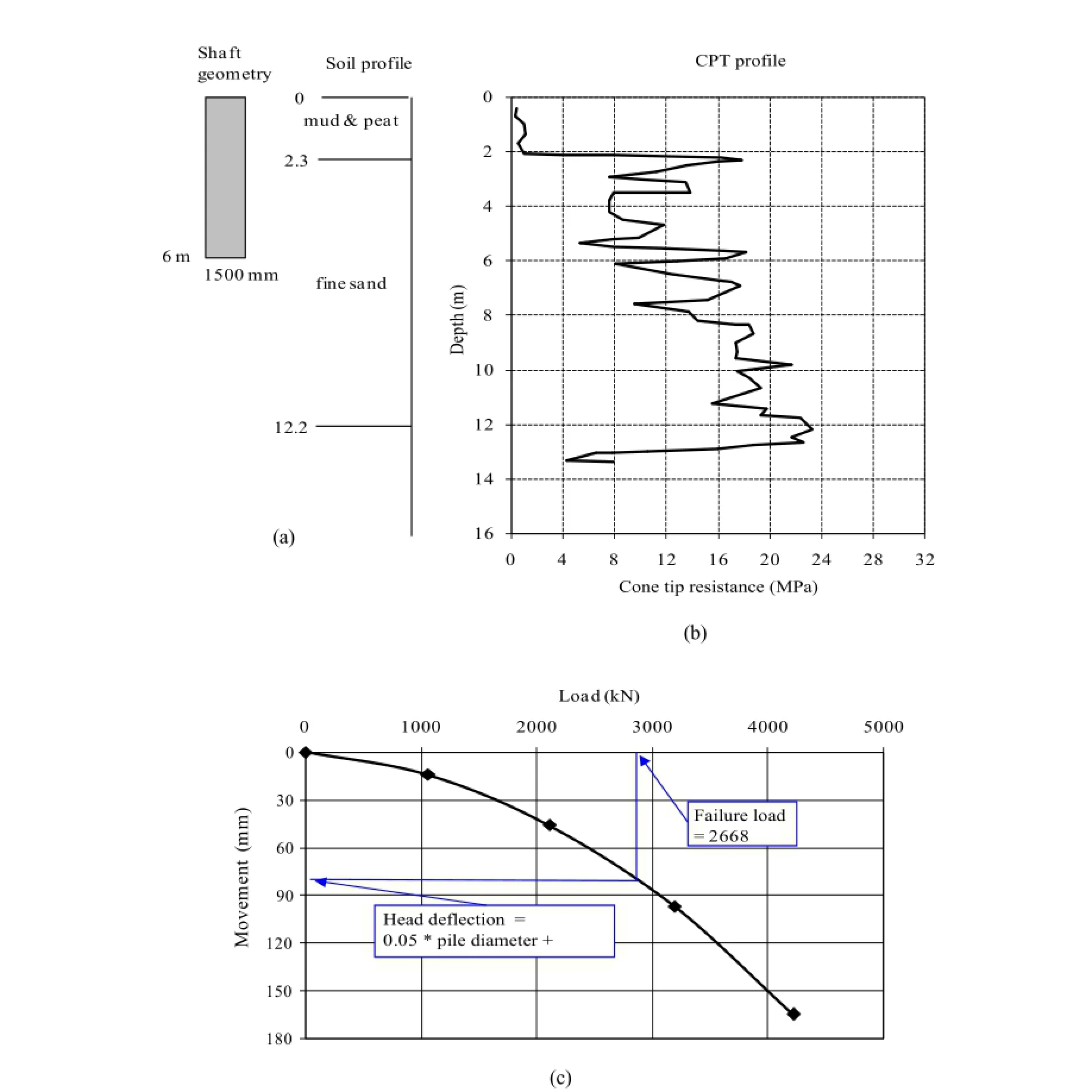
Fig.1.Summary sheet for selected case record:(a)pile geometry and soil pro fi le;(b)cone tip resistance pro fi le;(c)load-movement plot(Alkroosh and Nikraz,2011a,b).

3.2.Input and output variables

A proper estimation of bearing capacity of pile foundation requires the identi fi cation of the factors that in fl uence the pile-soil interaction.An extensive study of relevant existing literature was carried out and concluded that pile geometry and soil properties are the signi fi cant factors that affect the pile bearing capacity.

(1)Pile geometry

Allgeotechnicalengineering sources con fi rm that pile diameter and length have signi fi cant in fl uence on bearing capacity of pile foundations.Therefore,these factors were selected to represent pile geometry for input of LSSVM model(Eslami,1997;Teh et al., 1997;Abu-Kiefa,1998).

(2)Soil properties

The soil properties that have principal in fl uence on pile bearing capacity are mainly interpreted as the angle of internal friction,φ, relative density,Dr,earth pressure coef fi cient,K0,and cohesion,c. Many researchers have suggested correlations between these factors and CPT data,and proposed solutions for prediction of pile bearing capacity.However,indirect correlations of CPT data with pile bearing capacity have been found to give inaccurate estimate of pile bearing capacity due to considerable uncertainty resulting from the intermediate steps and correlations.Consequently,direct correlations of CPT results with pile bearing capacity have been suggested and found to give better results.

Thus,in this work,the CPT results were directly used as input variables based on the suggestions provided by the current CPT-based methods(e.g.Alsamman,1995;Eslami,1997).According to the methods,the cone point resistance measurements are averaged within pile tip in fl uence zone,which is a function of pile diameter, and used for calculating pile tip resistance.For smalldiameter piles, the in fl uence zone was taken based on the work done by Eslami (1997),while for large diameter piles the in fl uence zone was taken based on Alsamman(1995).The average cone point resistance along pile shaft was included as input,as most ofthe methods also suggest it to calculate pile shaft resistance.

In fact,the use of sleeve friction in calculation of bearing capacity is not recommended by number of commonly used CPT-based methods,such as Laboratoire Central des Pont et Chausees (LCPC),due to the unreliability of sleeve friction measurements (Alkroosh and Nikraz,2011a,b).

The mechanical cone point resistance was converted to equivalent electric values using Eq.(15)which was developed by Kulhawy and Mayne(1990):

where q c is the cone point resistance;p a is the atmospheric pressure,which is 101 kPa.

3.3.Pile bearing capacity,Qu

The interpreted failure load,Qu,was considered as the pile bearing capacity and calculated according to Alsamman(1995).The failure load was de fi ned as the measured axial load that corresponds to a displacement equal to 5%of pile diameter plus the elastic compression of the pile.Fig.1 presents the de fi nition of the failure load for a case record selected from the database.

3.4.LSSVM for predicting pile bearing capacity

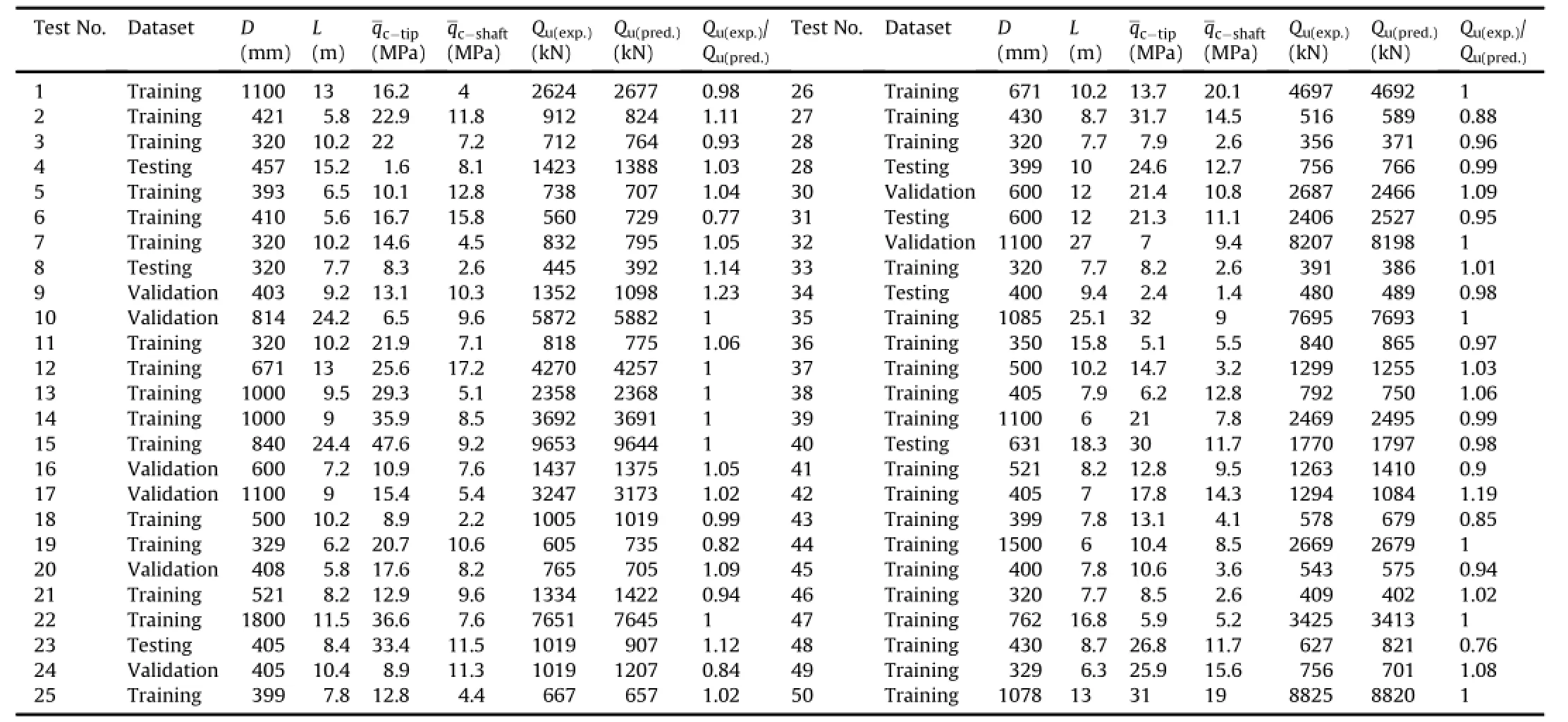
Table 1 Summary of database used in the application of LSSVM and the output results(Alkroosh and Nikraz,2011a,b).

The data were mapped into range[-1,1]using below equation:where x and xnare the original and normalized desired variables, respectively;xminand xmaxare the extreme values of the variable x. This pre-processing procedure was applied to obtain the parameters of the LSSVM algorithm.Later,these values were changed to their original values.

In the next step,the database was divided into three subsets including the training,testing and validation sets.The division of database into three subsets was normally performed randomly but considering the statisticalconsistency ofthe data ofthe subsets.For this purpose,70%,15%and 15%of the main dataset were randomly selected for building the LSSVM models(i.e.training,testing and validation sets,respectively).The allocated data for each subset are shown in Table 1.The effect of the percent allocation of the three subsets from the database on the accuracy of the fi nal model has been studied(Gharagheiziet al.,2011).As for the distribution of the data through the three subsets,we generally performed many distributions to avoid the local accumulations of the data in the feasible region of the problem.As a result,the acceptable distribution is the one with homogeneous accumulations of the data on the domain of the three subsets(Eslamimanesh et al.,2011).

4.Results and discussion

The ability of the LSSVMto predict the pile bearing capacity was evaluated primarily during the training phase by comparing the measured values of pile bearing capacity with the predicted values obtained by the LSSVM.When training phase was completed,it was expected that the proposed algorithm would correctly reproduce the targeted output values presuming the error is minimal.However,this was insuf fi cient to conclude that the trained LSSVM can predict the pile bearing capacity accurately as this technique,in general,has a high tendency towards over-fi tting.Over-fi tting refers to the large error in predictions when new data are presented to the trained LSSVM(i.e.ability of the LSSVM to memorize rather than generalize the form of the relationship between input and output data).Generally,over-fi tting is expected when data points in training sets are scanty(Das,2013).To overcome this setback,a testing dataset,not included in training data,was used to examine the predictive ability of LSSVM.If it was found to give accurate predictions,further evaluation was made to verify its generalization ability.This was done by examining the predictions of LSSVM through the use of validation dataset which was neither included among training nor testing datasets.Once the training testing and validation steps were successfully completed,the trained LSSVM can be recommended as a design tool for this type of application.

The predictions of pile bearing capacity by the LSSVMas well as other CPT-based methods including Schmertmann(1978), Bustamante and Gianeselli(1982),Alsamman(1995),and Alkroosh and Nikraz(2011a,b)were evaluated.A brief description of the compared methods is provided in Table 2.The results ofcomparison are shown numerically in Table 3 and graphically in Figs.2 and 3. Table 3 also presents the results ofstatisticalanalysis used to evaluate the accuracy ofthe proposed method.Five statisticalindices including coef fi cient of determination,R,mean,μ,standard deviation,σ,mean absolute error,MAE,and mean squared error,MSE,were used in the analysis.The coef fi cient ofdetermination is calculated by

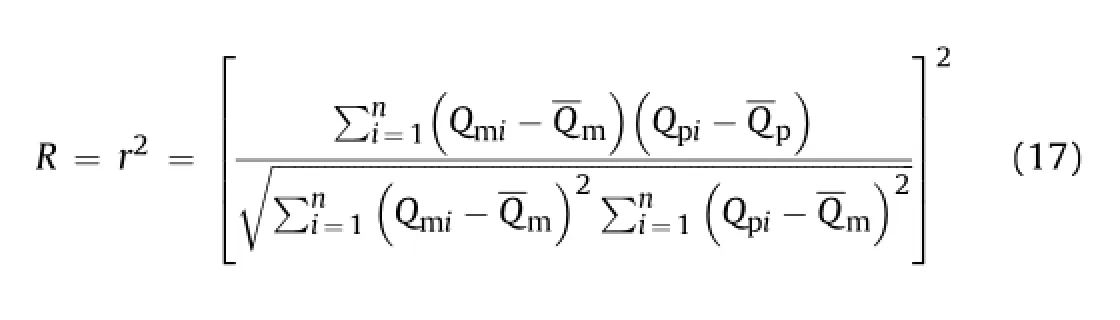
where r is the coef fi cient of correlation;Q m i and Q p i are the measured and predicted pile bearing capacity of case i,respec-are the averages of measured and predicted pile bearing capacity,respectively;n is the number of observations.

The optimalvalue of R is unity,which means that a perfect fi t is achieved between predicted and measured values.Table 3 shows that the calculated R=1 for the training and validation sets and R=0.99 for the testing set indicate that the LSSVMcan achieve an accurate correlation between predicted and measured pile bearing capacity.Table 3 also shows that the proposed method is more accurate than other methods.

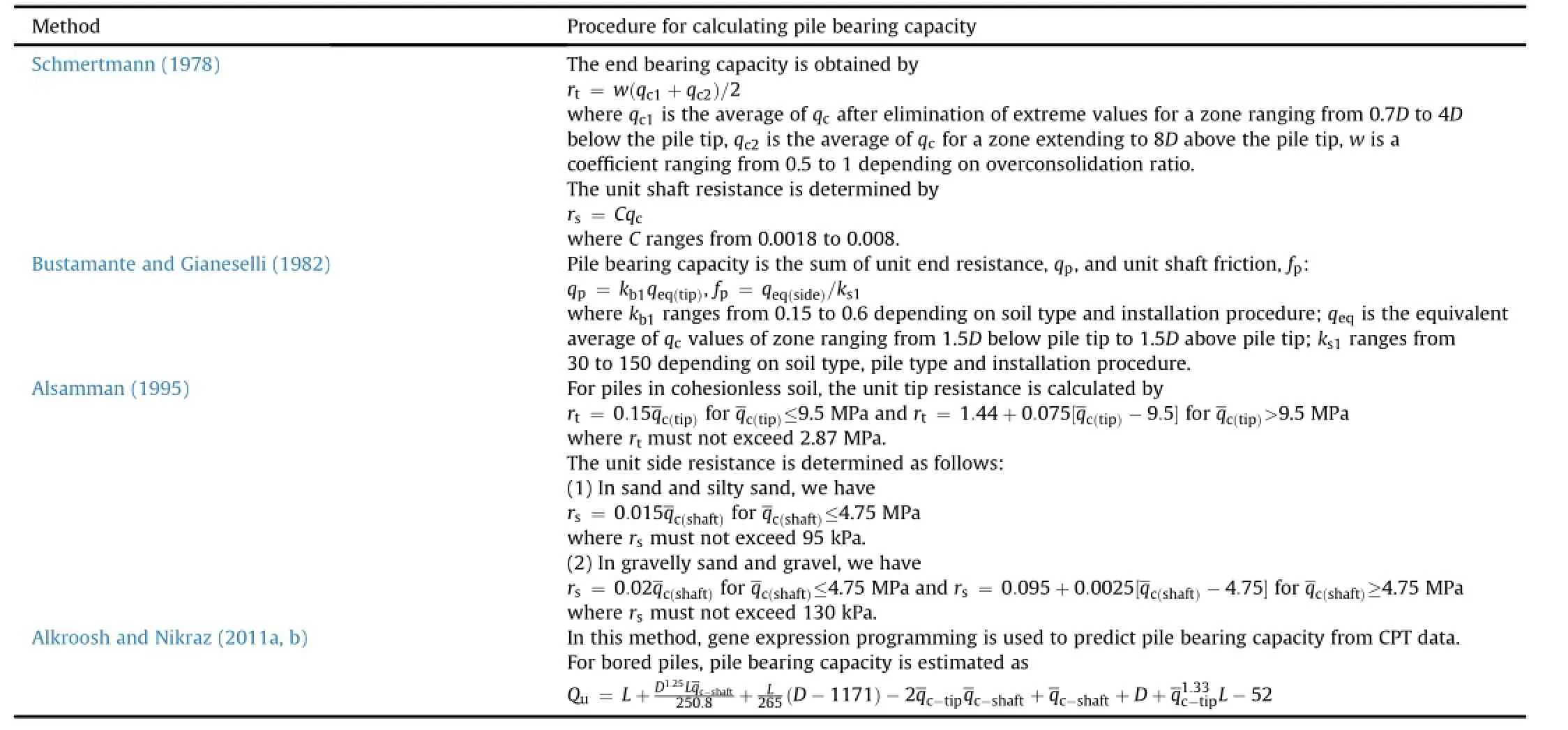
Table 2 Some CPT methods versus the LSSVM.

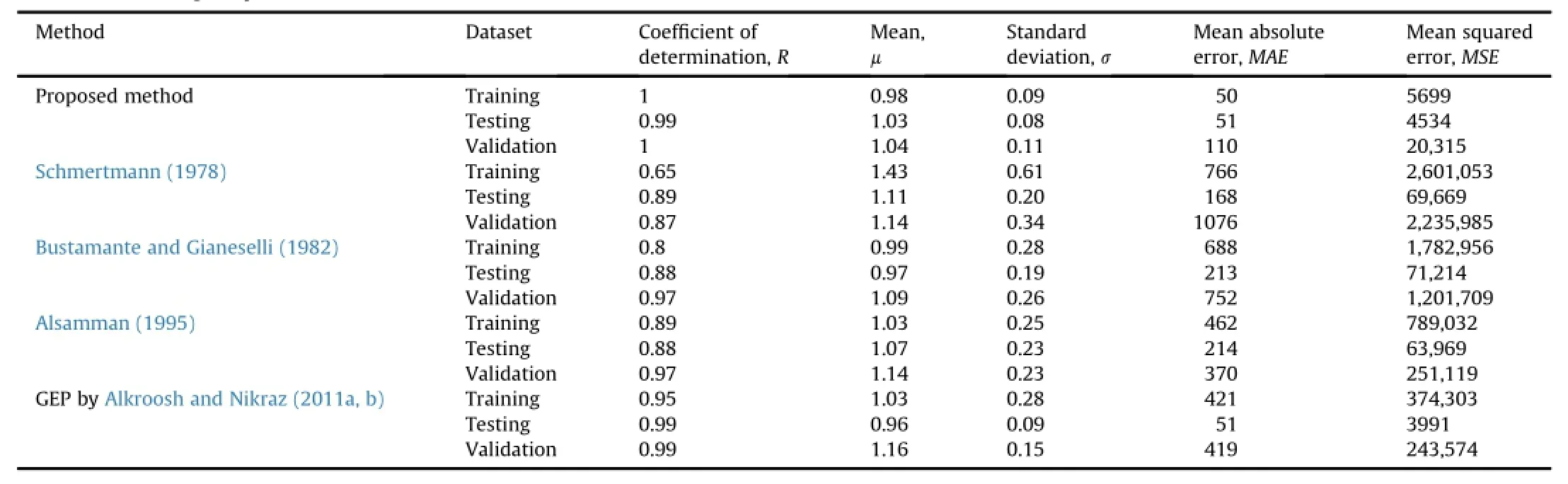
Table 3 Results of evaluating the performance of LSSVM.

Then the mean and standard deviation were respectively calculated by

If the mean value is unity,the predicted values of pile bearing capacity are on average equivalent to the measured values.A mean value of less than unity indicates that the method tends to underpredict the pile bearing capacity.Conversely,more than unity is an indication of over-prediction.The optimum value of standard deviation is zero;the closer the standard deviation approaches to zero,the greater the accuracy is.As presented in Table 3,the calculated mean values of the proposed method are 0.98,1.03 and 1.04 for the training,testing and validation sets,respectively,which indicate that the LSSVM possesses a high capability in predicting pile bearing capacity.The results also indicate that,on average,the proposed method may tend to over-predict the pile bearing capacity in testing and validation sets,whereas under-predict it in training set.In comparison with other methods,the calculated mean values indicate that the LSSVM provides better estimate for pile bearing capacity.

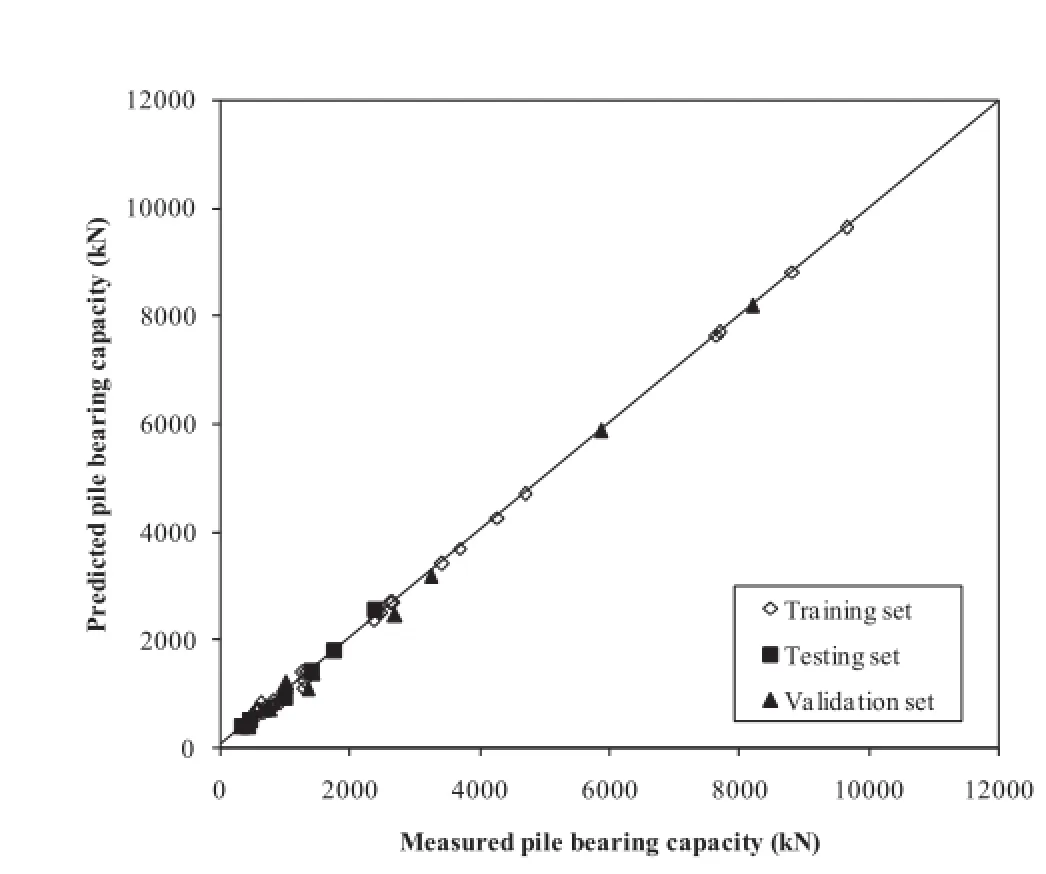
Fig.2.Performance of the LSSVM model in training,testing and validation sets.

The predictive ability of the LSSVM is also evaluated by calculating the error.Table 3 shows that the calculated MSE and MAE are low when using the proposed method to predict pile bearing capacity.The table also shows that the proposed method has the lowest error in comparison with other methods.

As shown in Fig.2,the strong ability of LSSVM to predict the pile bearing capacity is obvious.All the points in training,testing and validations sets are situated on or very close to the line of equality,suggesting that the proposed method is accurate in predicting the pile bearing capacity.Fig.3 shows that the LSSVM achieves very high correlation between predicted and measured values and it has the lowest scatter around the line of equality in comparison with other methods.From Fig.3,it is most evident that the LSSVM provides best prediction of total pile bearing capacity.

In order to verify whether or not the results of the proposed method agree with those in the existing literature and experimental results,the sensitivity analysis was carried out.In this analysis,values of one input variable were allowed to change within the range of the training data whereas the values of other input variables were set constant.The data were then input in the developed LSSVM and the outputs were evaluated.The results,as presented in Fig.4,have shown that the proportion between each input variable and the predicted pile bearing capacity is incremental,and the variations of pile diameter and average cone point resistance within pile tip infl uence zone and along pile shaft have great in fl uence on pile bearing capacity.The variation of pile length slightly affects pile bearing capacity.

5.Conclusions

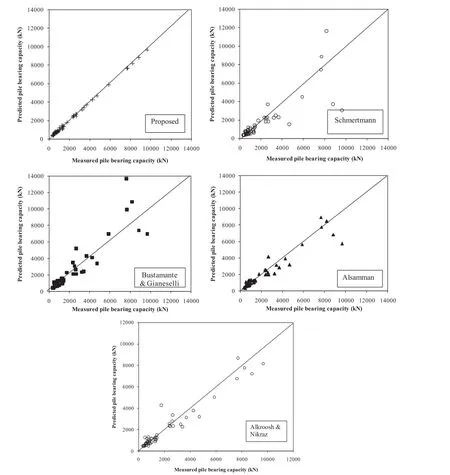
Fig.3.Comparisons ofthe performance of the LSSVM modelwith CPT-based methods.

The results of this study indicate that the proposed LSSVMcan accurately predict the bearing capacity of bored piles from CPT data.The statistical analysis of the results reveals that this technique can obtain coef fi cient of determination and mean close to unity for all training,testing and validation sets.It has also achieved standard deviation less than 0.2 and low error values. The comparisons of the predictive ability of LSSVM with traditional CPT-based methods as well as the GEP model have shown that this technique predicts pile bearing capacity better.The relationship of pile bearing capacity with each of pile diameter, length,average of cone point resistance is incremental.The average cone point resistance within pile tip zone is the most in fl uential factor on pile bearing capacity.The output of this study suggests that LSSVM can be used as a design tool forpredicting the bearing capacity of bored piles installed in sand and mixed soils.

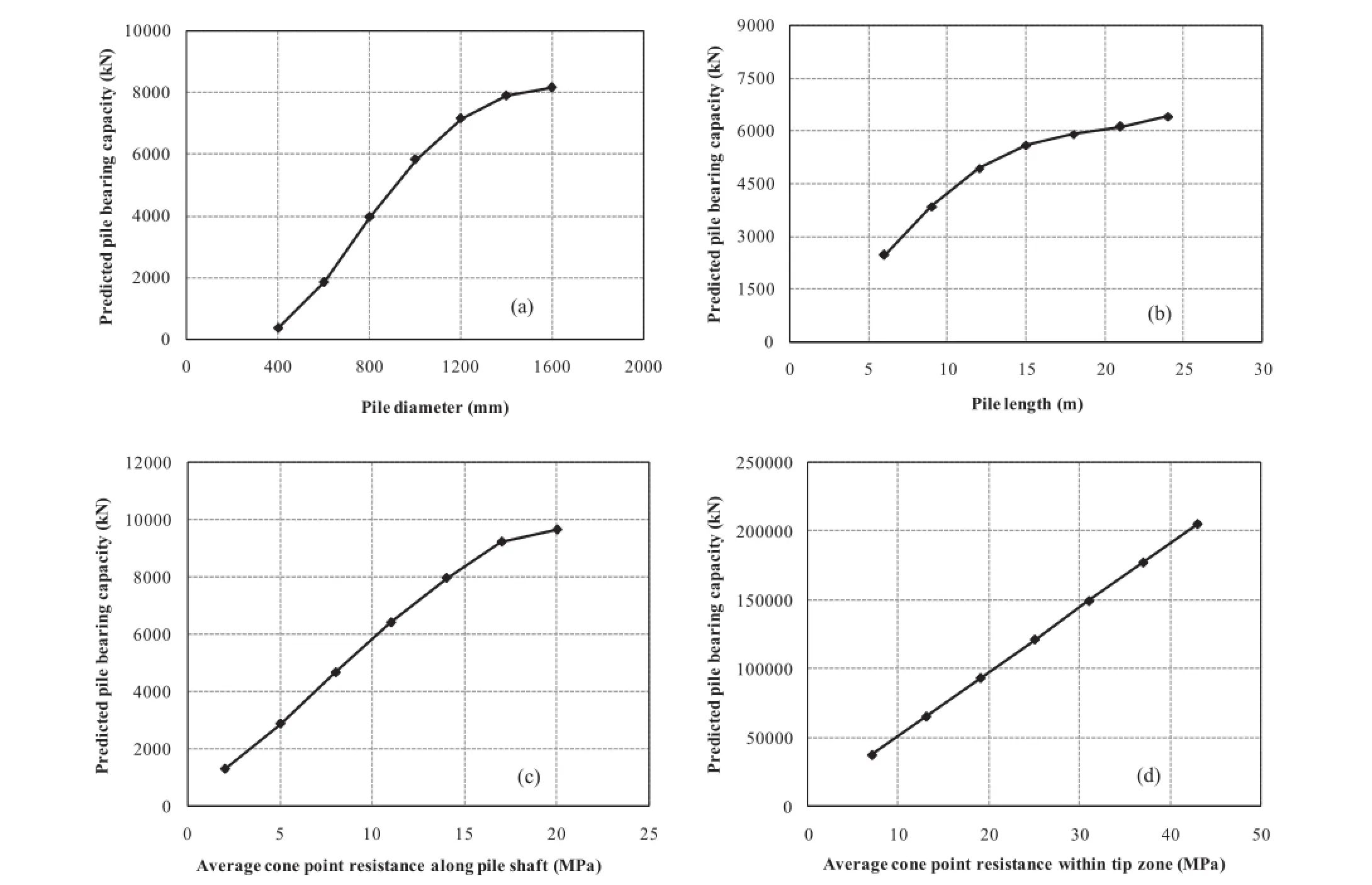
Fig.4.Effects of variations of input variables on pile bearing capacity:(a)pile diameter;(b)pile length;(c)average cone point resistance along shaft;(d)average cone point resistance within tip zone.

Con fl ict of interest

The authors con fi rm that there are no known con fl icts of interest associated with this publication and there has been no signi fi cant fi nancialsupportforthis work thatcould have in fl uencedits outcome.

Abu-Farsakh M,Titi H.Assessment of direct cone penetration test methods for predicting the ultimate capacity offriction driven piles.Journalof Geotechnical and Environmental Engineering 2004;130(9):935-44.

Abu-Kiefa MA.General regression neural networks for driven piles in cohesionless soils.Journalof Geotechnicaland GeoenvironmentalEngineering 1998;124(12): 1177-85.

Alavi AH,Aminian P,Gandomi AH,Esmaeili MA.Genetic based modeling of uplift capacity of suction caissons.Expert Systems with Applications 2011;38(10): 12608-18.

Alkroosh I,Nikraz H.Correlation of pile axial capacity and CPT data using gene expression programming.Geotechnical and Geological Journal 2011a;29(5): 725-48.

Alkroosh I,Nikraz H.Predicting axialcapacity ofdriven piles in cohesive soils using intelligent computing.Engineering Applications of Arti fi cial Intelligence 2011b;25(3):618-27.

Alsamman O.The use of the CPT for calculating axial capacity of drilled shafts.PhD Thesis.Urbana,USA:University of Illinois at Urbana;1995.

Amendolia SR,Cossu G,Ganadu ML,Golosio B,Masala GL,Mura GM.A comparative study of K-nearest neighbour,support vector machine and multi-layer perceptron for Thalassemia screening.Chemometrics and Intelligent Laboratory Systems 2003;69(1-2):13-20.

Ardalan H,EslamiA,Nariman-Zadeh N.Piles shaftcapacity from CPT and CPTU data by polynomial neural networks and genetic algorithms.Computers and Geotechnics 2009;36(4):616-25.

Baylar A,Hanbay D,Batan M.Application ofleastsquare support vector machines in the prediction of aeration performance of plunging overfall jets from weirs. Expert Systems with Applications 2009;36(4):8368-74.

Bazzani A,Bevilacqua A,Bollini D,Brancaccio R,Campanini R,Lanconelli N, Riccardi A,Romani D.An SVM classi fi er to separate false signals from microcalci fi cations in digital mammograms.Physics in Medicine and Biology 2001;46(6):1651.

Briaud J.Evaluation of cone penetration test methods using 98 pile load tests.In: Proceedings of the 1st International Symposium on Penetration TestingVol.2. Rotterdam,Netherlands:A.A.Balkema;1988.p.687-97.

Bustamante M,Gianeselli L.Pile bearing capacity prediction by means of static penetrometer CPT.In:Proceedings of the 2nd European Symposium on Penetration Testing,ESOPT-II,Amsterdam,The Netherland;1982.p.493-500.

Cai G,Liu S,Tong L,Du G.Assessment of direct CPT and CPTU methods for predicting the ultimate bearing capacity of single piles.Engineering Geology 2008;104(3-4):211-22.

Chamkalani A,Amani M,Kiani MA,Chamkalani R.Assessment of asphaltene deposition due to titration technique.Fluid Phase Equilibria 2013;339:72-80.

Chen TS,Chen J,Lin YC,Tsai YC,Kao YH,Wu KS.A novel knowledge protection technique based on support vector machine model for anti-classifi cation.In:Electricalengineering and control.Berlin,Germany:Springer;2011. p.517-24.

Cortes C,Vapnik V.Support-vector networks.Machine Learning 1995;20(3):273-97.

Das S,Samui P,Kim D,Sivakugan N,Biswal R.Lateral displacement of liquefaction induced ground using least square support vector machine.International Journal of Geotechnical Earthquake Engineering 2011b;2(2):29-39.

Das S,Samui P,Kothari D.Site characterization model using machine learning.In: Machine tools:design,reliability and safety.New York,USA:Nova Science Publishers Inc.;2011a.p.175-85.

Das SK,Basudhar PK.Undrained lateral load capacity of piles in clay using arti fi cial neural network.Computers and Geotechnics 2006;33(8):454-9.

Das SK.Arti fi cial neural networks in geotechnical engineering:modeling and application issues.In:Yan X,Gandomi AH,Talatahati S,Alavi AH,editors. Metaheuristics in water;2013.p.231-70.

Deng S,Yeh TH.Applying least squares support vector machines to the airframe wing-box structural design cost estimation.Expert Systems with Applications 2010;37(12):8417-23.

Eslami A.Bearing capacity of piles from cone penetration data.PhD Thesis.Ottawa, Canada:University of Ottawa;1997.

Eslamimanesh A,Gharagheizi F,Mohammadi AH,Richon D.Phase equilibrium modeling of structure H clathrate hydrates of methane+water“insoluble”hydrocarbon promoter using group contribution-support vector machine technique.Industrial and Engineering Chemistry Research 2011;50(20): 12807-14.

Gandomi AH,Alavi AH.A new multi-gene genetic programming approach to nonlinear system modeling.Part II:geotechnical and earthquake engineering problems.Neural Computing and Applications 2012;21(1):189-201.

Gandomi AH.Nonlinear genetic based models for prediction of fl ow number of asphalt mixtures.Journal of Materials in Civil Engineering 2011;23(3):248-63. Gharagheizi F,Eslamimanesh A,Farjood F,Mohammadi AH,Richon D.Solubility parameters of nonelectrolyte organic compounds:determination using quantitative structure-property relationship strategy.Industrial and Engineering Chemistry Research 2011;50(19):11382-95.

Gunn SR.Support vector machines for classi fi cation and regression.Technical report.Southampton,UK:Faculty of Engineering,Science and Mathematics, Schoolof Electronics and Computer Science,University of Southampton;1998. Kulhawy F,Mayne P.Manual on estimating soil properties for foundation design. Palo Alto,CA,USA:Electric Power Research Institute;1990.

Minoux M.Mathematical programming:theory and algorithms.New York,USA: Wiley;1986.

Müller KR,Mika S,R?tsch G,Tsuda K,Sch?lkopf B.An introduction to kernel-based learning algorithms.IEEE Transactions on Neural Networks 2001;12(2):181-201.

Ng C,Simons W,Menzies B.Soil-structure engineering of deep foundations,excavations and tunnels.London,UK:Thomas Telford Ltd.;2004.

Ornek M,Laman M,Demir A,Yildiz A.Prediction of bearing capacity of circular footings on soft clay stabilized with granular soil.Soils and Foundations 2012;52(1):69-80.

Ra fi ee-Taghanaki S,Arabloo M,ChamkalaniA,AmaniM,ZargariMH,Adelzadeh MR. Implementation of SVM framework to estimate PVT properties of reservoir oil. Fluid Phase Equilibria 2013;346:25-32.

Rezania M,Javadi A.A new genetic programming model for predicting settlement of shallow foundations.Canadian Geotechnical Journal 2007;44(12):1462-73. Roberston P,Campanella R,Davies M,Sy A.Axialcapacity ofdriven piles in deltaic soils using CPT.In:Proceedings of the 1st International Symposium on Penetration TestingVol.2.Rotterdam,Netherlands:A.A.Balkema;1988.p.919-28. Samui P,Kothari DP.Utilization of a least square support vector machine(LSSVM) for slop stability analysis.Scientia Iranica 2011;18(1):53-8.

Schmertmann JH.Guidelines for cone penetration test,performance and design. Washington D.C.,USA:US Department of Transportation;1978.

Shahin M.Intelligent computing for modeling axial capacity of pile foundations. Canadian Geotechnical Journal 2010;47(2):230-43.

Shokrollahi A,Arabloo M,Gharagheizi F,Mohammadi AH.Intelligent model for prediction of CO2-reservoir oil minimum miscibility pressure.Fuel 2013;112: 375-84.

Suykens JA,Van Gestel T,De Brabanter J,De Moor B,Vandewalle J.Least squares support vector machines.Singapore:World Scienti fi c Publishing Company; 2002.

Suykens JA,Vandewalle J.Least squares support vector machine classi fi ers.Neural Processing Letters 1999;9(3):293-300.

Tarawneh B.Pipe pile setup:database and prediction modelusing arti fi cialneural network.Soils and Foundations 2013;53(4):607-15.

Teh CI,Wong KS,Goh AT,Jaritngam S.Prediction of pile capacity using neural networks.Journal of Computing in Civil Engineering 1997;11(2):129-38.

übeyli ED.Least squares support vector machine employing model-based methods coef fi cients for analysis of EEG signals.Expert Systems with Applications 2010;37(1):233-9.

Xavier-de-Souza S,Suykens JA,Vandewalle J,Bolle D.Coupled simulated annealing. IEEE Transactions on Systems,Man,and Cybernetics.Part B:Cybernetics 2009;40(2):320-35.

Dr.Iyad Alkrooshbegan his career as a civilengineer after graduation from University of Technology Baghdad in 1987.He received his MSc and PhD degrees in civilengineering from Curtin University,Western Australia in 2000 and 2011,respectively.Currently he has been a lecturer at Department of Civil Engineering,College of Engineering, Al-Qadisiya University,Iraq.Since 2011,Dr.Alkroosh has been working as a consultant for the Scienti fi c and Engineering Bureau,Al-Qadisiya University.His fi eld ofinterest includes but not limited to modeling using arti fi cial intelligence,load transfer behavior of piles,soil improvement, and structural design of shallow and deep foundations. Dr.Alkroosh is the author of 15 publications in international journals and conferences.

Mohammad Bahadoriis a research student in the Department of Soil Science and Engineering at the University of Tehran,Iran.He received his BSc degree from Shahaid Chamran University,Ahwaz,Iran and his MSc degree from the University of Tehran,Iran.

Dr.Hamid Nikrazis a professor at the Department of Civil Engineering,School of Engineering,Curtin University, Australia.Prior to his academic career he had many years’experience working in industry in the Middle East,Europe and Australia.He has provided numerous consultancy services in his fi eld to over 200 organizations nationally and internationally.He obtained his PhD at Curtin University of Technology in 1989.Dr.Nikraz is a Fellow Member of the Institution of Engineers,Australia.He has guided 75 PhD theses,30 Master students and published over 500 publications in various journals,books and conference proceedings.Prof.Nikraz has initiated research works in the area of Geopolymers,Concrete,Soil Stabilisation and Pavement Engineering.Prof.Nikraz is also the reviewer of many national and international journals.

Alireza Bahadori,PhD,P.Eng,MIEAust.,is a research staff member and lecturer in the School of Environment,Science and Engineering at Southern Cross University,Lismore,NSW,Australia.He received his PhD from Curtin University,Perth,Western Australia.During the past twenty years,Dr.Bahadori has held various process and petroleum engineering positions and was involved in many large-scale projects at National Iranian Oil Co. (NIOC),Petroleum Development Oman(PDO),and Clough AMEC Pty Ltd.He is the author of several articles and books.His books have been published by multiple major publishers,including Elsevier,Springer,John Wiley& Sons,and Taylor and Francis Group.Dr.Bahadori is the recipientofthe highly competitive and prestigious Australian Government’s Endeavour International Postgraduate Research Award as part of his research in oiland gas area.He also received a Top-Up Award from the State Government of Western Australia through Western Australia Energy Research Alliance in 2009.Dr.Bahadori serves as a member of the editorial board and reviewer for a large number ofjournals.He is member ofthe Institution of Engineers Australia as a professional engineer and IChemE,UK.

*Corresponding author.Tel.:+61 2 6626 9347.

E-mail address:Alireza.bahadori@scu.edu.au(A.Bahadori).

Peer review under responsibility of Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.

1674-7755?2015 Institute of Rock and Soil Mechanics,Chinese Academy of Sciences.Production and hosting by Elsevier B.V.All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2015.06.011