Xue Gaoping; Weng Huixin; Thybaut Joris W.; Marin Guy B.

(1. Research Institute of Petroleum Processing, East China University of Science and Technology, Shanghai 200237; 2. Laboratory for Chemical Technology, Ghent University, Ghent, B-9000, Belgium)

Catalytic Cracking of Cycloparaffins Admixed with Olefins: 1. Single-Event Microkinetic (SEMK) Modeling

Xue Gaoping1,2; Weng Huixin1; Thybaut Joris W.2; Marin Guy B.2

(1. Research Institute of Petroleum Processing, East China University of Science and Technology, Shanghai 200237; 2. Laboratory for Chemical Technology, Ghent University, Ghent, B-9000, Belgium)

Single-event microkinetic (SEMK) model of the catalytic cracking of methylcyclohexane admixed with 1-octene over REUSY zeolites at 693 K—753 K in the absence of coke formation is enhanced. To keep consistency with the wellknown carbenium ion chemistry, hydride transfer forming and consuming allylic carbenium ions in the aromatization of cycloparaffins are further investigated and differentiated. The reversibility of endocyclic β-scission and cyclization reactions is refined by accounting explicitly for the reacting olefins and resulting cycloparaffins in the corresponding thermodynamics. 24 activation energies for the reactions involved in the cracking of cycloparaffins are obtained by the regression of 15 sets of experimental data upon taking the resulting 37 main cracking products,i. e., responses into account. The enhanced SEMK model can adequately describe the catalytic behavior of 37 main products with conversion and temperature.

catalytic cracking; single-event microkinetic model; cycloparaffin; olefin; catalysis

1 Introduction

As one of the most important refinery processes, fluid catalytic cracking (FCC) has been receiving continuous attention over the past 50 years[1]. The performance of a FCC unit is mainly determined by three factors, viz.: (i) the feedstock’s characteristics, (ii) the operating conditions, and (iii) the nature of the catalyst. It has been qualitatively pointed out that the properties of the feedstock do affect the performance of FCC process mostly[2].

In general acyclic hydrocarbons, cyclic hydrocarbons and aromatics are the three main components in typical FCC feedstocks. Due to the relatively simple reaction networks, the cracking of acyclic hydrocarbons and aromatics has been extensively studied by different groups[3-5], while the cracking of cyclics received less attention[6-13]. During the cracking of cyclic hydrocarbons, ring-opening cracking and aromatization reactions play significant roles, in addition to the reactions occurring in the cracking of acyclic hydrocarbons and aromatics. Because of the pronounced differences between octane numbers of acyclic hydrocarbons and aromatics, the relative contribution of the ring-opening cracking and aromatization reactions in the cracking of cyclic hydrocarbons is of primary importance to the quality of the FCC gasoline. Moreover, aromatics tend to be converted into other aromatics and acyclic hydrocarbons into other acyclic hydrocarbons while cyclics can be significantly converted into acyclic hydrocarbons and aromatics. Hence, it can be said that the cracking of cyclics plays a decisive role in the production of high-quality gasoline via FCC reactions.

Till now, only a few studies have paid attention to the catalytic conversion of cyclic hydrocarbons under industrially relevant conditions[6-13]. Particularly, methylcyclohexane has been recognized as a suitable model molecule for representing the catalytic cracking of cycloparaffins due to its simple structure and relatively less complex cracking network[14-17]. Cerqueira, et al.[14]studied the conversion of methylcyclohexane at 450 ℃ over HFAU, HBEA and HMFI zeolites to address the effect of the acidity and pore structure of the catalyst on the transformation of methylcyclohexane. Al-Sabawi, et al.[15]investigated the cracking of methylcyclohexane under industrially relevant FCC conditions and developed a lumped kinetic model which accounted for the effect of the adsorption and dif-fusion of hydrocarbons in the USY zeolite. Marques, et al.[16]carried out methylcyclohexane cracking experiments over dealuminated HBEA samples treated by three different methods and correlated the methylcyclohexane protolytic scission and carbenium ion chain cracking rate to the concentration of protonic sites and Lewis sites, respectively. From the above, it can be seen that kinetic studies on the cracking of cycloparaffins are relatively scarce compared to the cracking of acyclic hydrocarbons. Moreover, most of the reported kinetic models were in lumped form where the parameters of the model strongly depend on the feedstock properties[7,14-15]. The singleevent microkinetic (SEMK) methodology is one of the most effective approaches to investigate the detailed catalytic reaction behavior at the molecular level[17-20], with the model parameters being invariant to the nature of the feedstock[21]. The methodology was first applied to the catalytic cracking of paraffins by Feng, et al.[3]. Quintana-Solórzano, et al.[22]further extended its application to the catalytic cracking of cycloparaffins. However, Quintana-Solórzano, et al.[22]only concerned the easier formation of allylic carbenium ions and did not consider their more difficult conversion compared to non-allylic carbenium ions. In this work, we describe the development of an enhanced SEMK model that has been applied in the simulation of catalytic cracking of cycloparaffins admixed with olefins. The emphasis is put on differentiating between all reactions involving allylic carbenium ions and those involving simple carbenium ions. The enhanced SEMK model has been validated by comparing the calculated yields of the main products with the experimental ones and by analyzing the obtained parameters in physical and statistical terms.

2 Procedures

2.1 Experimental

Experiments have been performed previously on a commercial REUSY zeolite in a TEOM?microbalance reactor[23]. Methylcyclohexane was used as the feedstock admixed with 17.65% (molar fraction) of 1-octene to initiate feedstock conversion more easily. The reaction temperature ranged from 693 K to 753 K where thermal cracking was confirmed to play a negligible role in the cracking system. A space-time between 12.09 and 42.30 kgcat·s/mol was applied to cover a broad range of methylcyclohexane conversions, i.e., between 9.7% and 54.5%. Under these reaction conditions, the absence of transport limitations in the pores of the catalyst has been con firmed. More experimental details can be found elsewhere[23]. The molar yields of various products collected at a time on stream of 1.5 min, which was close to time zero, were assumed not to be affected by coke formation and used to estimate the parameters.

2.2 Parameter determination

2.2.1 Calculation of the pre-exponential factors

In order to reduce the number of parameters to be determined, the pre-exponential factors were calculateda prioriusing statistical thermodynamics and transition state theory by making some reasonable assumptions about the mobility and chemical bonding of the transition state involved in each elementary reaction to the catalyst surface[22,24-25]. One pre-exponential factor was calculated and assigned to each reaction family. Typical values calculated by Quintana-Solórzano, et al.[22]were used and fixed during the estimation of activation energies for the relevant reactions.

2.2.2 Regression of the activation energies to experimental data

The SEMK model parameters were estimated by minimizing the objective function defined as the weighted residual sum of squares of the experimental molar yieldsand the calculated onesof the various responses.

15 sets of experimental data with a mixture of methylcyclohexane and 1-octene serving as the feedstock at three different temperatures were used to estimate the activation energies for the elementary reactions involving cyclic species. The values obtained by Gaoping, et al[26]were adopted for the activation energies of the elementary reactions involving acyclic hydrocarbon species and kept fixed in the regression procedure.

Lumps, the molar yields of which were below 5×10-3mol·s-1/ (mol·s-1), were not considered in the objective function due to their relatively low concentrations in the reactor effluent.The weighting factors are calculated from an empirical formula as shown below[3]:

in whichαis equal to 0.4.

The reactor was assumed to be operating isothermally without any pressure drop. By assuming a pseudo-homogeneous one-dimensional plug flow model, a set of ordinary differential equations (ODEs) for all products were obtained.

Integration of these ODEs were performed by means of LSODE subroutine at Netlib[27]. The objective function SSQ was minimized by a combination of the Rosenbrock[28]and Levenberg-Marquardt[29]algorithm.

3 Single-Event Microkinetic Model Development

3.1 Network generation

The complex reaction networks of hydrocarbon catalytic cracking comprise hundreds, if not thousands, of elementary reactions and is automatically generated by a computer algorithm[21]. In addition to the elementary reactions occurring on acyclic hydrocarbon species, i.e., olefin (de) protonation, hydride transfer, carbenium ion isomerization including PCP-branching, hydride shift and methyl shift, β-scission and alkylation, more reactions can take place on cyclic hydrocarbon species (see Table 1). At present, the maximum carbon atom number of hydrocarbons in the reaction network generation is 12. This means that all the elementary reactions involving hydrocarbons containing less than 12 carbon atoms are explicitly accounted for in the reaction network.

Table 1 Single-event rate coefficients relevant to cyclic hydrocarbons and aromatics in the enhanced SEMK model of the catalytic cracking of methylcyclohexane

3.2 SEMK model parameters specifically accounting for reactions involving allylic carbenium ions

According to the single-event concept, the contribution of the symmetry of the reactant and the transition state to rate coefficientkis accounted for by the number of single events,ne. The remainder of the coefficient,i.e., the single-event rate coefficient,k～, is assumed to be only dependent on the reaction families and the type of the participating carbenium ions[21]. The single-event rate coefficients of the elementary reactions involving acyclic hydrocarbons have been well defined by Feng, et al.[3]and were used as such in this work. Similarly, Quintana-Solórzano, et al.[22]defined the single-event rate coefficients of the elementary reactions involving cyclic and aromatic hydrocarbons, i.e., those shown in Table 1 without asterisks. However, no distinction was made between reactions involving allylic carbenium ions and non-allylic carbenium ions in the work of Quintana-Solórzano, et al[22]. This simplification was not fully consistent with carbenium ion chemistry and further exploration of these reactions is thus required.

Being different from normal carbenium ions, allylic carbenium ions have a special structure in which the double bond and the positive charge conjugate together. Therefore, the elementary reactions involving allylic carbenium ions are expected to be different from those involving normal carbenium ions. In comparison with (de)protonation reactions involving normal carbenium ions, (de)protonation reactions involving allylic carbenium ions,andas shown in Table 1, are proposed in this work. With respect to hydride transfer reactions involving allylic carbenium ions, reactions relating to formation and consumption of these carbenium ions,as shown in Table 1, need to be distinguished. In general, the aromatization of cycloparaffins is viewed as a sequence of hydride transfer and deprotonation reactions[16](see Figure 1 for the aromatization of methylcyclohexane as an example). Methylcyclohexane at first undergoes hydride transfer with any available carbenium ion to form methylcyclohexyl. The latter subsequently transforms into methylcyclohexene via deprotonation. The second hydride transfer reaction from the scheme takes place on methylcyclohexene to yield methyl cyclic olefinic carbenium ion, which is a cyclic allylic carbenium ion that can be deprotonated to methylcyclohexadiene. The resulting cyclic diolefin undergoes again the same elementary reactions via an allylic carbenium ion, i.e., hydride transfer followed by deprotonation to ultimately form toluene. The reverse reaction, i.e., dearomatization of aromatics, follows the same sequence in the reverse direction to produce cycloparaffins.

Figure 1 Schematic representation of methylcyclohexane aromatization as a sequence of hydride transfer and deprotonation reactions

Among all the elementary reactions in the aromatization process, (de)protonation of cyclic hydrocarbons were found to be prone to occur in the cracking of alkylcyclohexane as referred to by Watson, et al.[17]. Along this line of thought, hydride transfer reactions involved in the aromatization are the key steps to account for the high tendency of cycloparaffins yielding aromatics and the refractoriness of aromatics to withstand further cracking reactions.

Owing to the charge delocalization and resonance effect of the allylic structure, allylic carbenium ions can be considered to be more stable than non-allylic ones. Hence, it is reasonable to assume that hydride transfer reactions consuming allylic carbenium ions, denoted as htr_c in Figure. 1, are energetically more demanding and, hence, more difficult, than those forming allylic carbenium ions, represented as htr_a. In this way the easier tendency of aromatization than that of dearomatization should be reasonably explained by the difference between hydride transfer reactions consuming and forming allylic carbenium ions. As a consequence, a distinction between thesehydride transfer reactions consuming and forming allylic species is made and the activation energy of the former is expected to exceed that of the latter.

The disproportionation reactions between aromatics are also included in this work to comprehensively account for the reactions involving aromatics.

3.3 Relumping scheme

Due to the limitations of the present day analytical techniques, the complete characterization of individual molecules that are present in the feed and products of FCC process is not possible yet[23]. Thus it is unrealistic to fully address the catalytic behavior of hydrocarbons at the molecular level. Hence, some degree of lumping of the giant reaction network is inevitable[3,22].

3.3.1 Definition of lumps

For cyclic hydrocarbons, lumps are defined by the ring size,i.e., the 5- or 6-membered ring and the number of substituents on the ring, as well as by its carbon number. Aromatics lumps are determined by the number of substituents on the aromatic ring and the carbon number. The acyclic hydrocarbons lumps are dictated by the carbon number and the branching degree. When grouping acyclic hydrocarbons into a lump based on the above method, thermodynamic equilibrium is assumed to be established in this lump because of the fast isomerization reactions between the components in the lump compared to the isomerization and cracking reactions occurring between the lumps[3], and upon grouping cyclics and aromatics to their corresponding lumps, an equimolar composition in this lump is assumed for simplicity purpose. A lumped reaction rate is calculated by summation of the rates of all elementary steps occurring between the lumps involved in the reaction. The details with respect to relumping have been reported elsewhere[3,21,30-31].

3.3.2 Thermodynamic consistency on the reversibility between cyclization and endocyclic β-scission

In the relumping scheme, thermodynamic consistency has been explicitly accounted for in the case of reversible reactions. Analogous to the reversibility between β-scission and alkylation reactions of acyclic hydrocarbons, cyclization reactions are the reverse reactions of endocyclic β-scissions in the cracking of cyclic hydrocarbons[3,32].

Upon considering the cyclization of olefinshown in Figure 2 as an example, the ole finundergoes hydride transfer yielding an allylic carbenium ionwhich goes through hydride shift reaction to break down the allylic structure to an ole finic carbenium ionThe latter then subsequently undergoes a conventional hydride shift reaction to yield another olefinic carbenium ionin which there are at least two carbon atoms between the double bond and the positive charge. Such a structure can undergo cyclization towards a cyclic carbenium ionwhich can produce cycloalkanevia hydride transfer or cycloalkenevia deprotonation.

Figure 2 The cyclization of olefins to cycloparaffins or cyclic olefins in elementary terms

The derivation of the constraints on the model parameters due to the thermodynamic consistency with respect to cyclization and endocyclic β-scission starts by considering the actual, elementary cyclization reaction betweenand, i.e., cyc and edβ as shown in Figure 2:

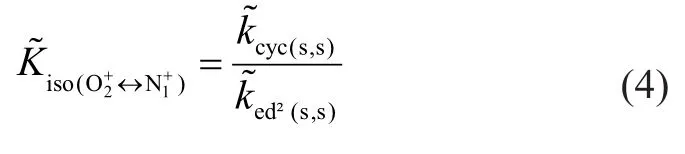
Then this reversibility relationship for the whole process incorporating O1and N1can be written as:

In this way, the cyclization single-event rate coefficientcould be expressed in terms of that of hydride transfer reactions on paraffins and cycloparaffins as well as that of endocyclic β-scission reactions. The analogous relations can be derived and applied to the other singleevent rate coefficients of cyclizationAs a consequence, the cyclization rate coefficients do not explicitly appear in the SEMK model but are implicitly expressed in terms of the rate coefficients of the corresponding endocyclic β-scission reactions.

4 Results and Discussion

Table 2 lists the estimated activation energies and corresponding individual confidence intervals at the 95% probability level for the reactions involved in the cycloparaffins cracking. Since the endocyclic β-scission (t, t) reaction does not occur in the cracking of methylcyclohexane, its rate coefficient cannot be estimated.

By taking into account the individual confidence intervals, all the estimated activation energies in the enhanced SEMK model are in accordance with what can be expected from free carbenium ion chemistry. Activation energies of reactions, such as pro_n and htr_n that form secondary cyclic carbenium ions, are higher than those of the same reaction family that form tertiary intermediates, whereas the deprotonation of tertiary cyclic carbenium ions requires higher activation energy than that of secondary ones. With respect to the reactions involving two types of cyclic carbenium ions, i.e., PCP_n and edβ, reactions transforming tertiary cyclic carbenium ions are more difficult to take place than those converting secondary ones.

Table 2 Estimated activation energies (kJ/mol) and their corresponding 95% confidence intervals obtained via the regression of the cracking data of methylcyclohexane and 1-octene

Besides being qualitatively assessed by carbenium ion chemistry, the obtained activation energies are also quantitatively in line with the relevant literature. For protolytic scission, the obtained activation energies were practically independent of the type of carbenium ions formed. The actual values agree quite well with those reported by Quintana-Solórzano, et al.[22]Moreover, there is no signif icant difference between the activation energy resulted from protolysis of cycloparaffins obtained in this work and that of protolysis of paraffins as reported by Corma, et al.[33].

The activation energies for (de)protonation involving secondary cyclic carbenium ions agree with those reported by Quintana-Solórzano, et al.[22]. Although those activation energies for (de)protonation involving tertiary cyclic carbenium ions deviate somewhat more pronouncedly, the (de)protonation enthalpy remains the same. The protona-tion enthalpy towards secondary cycloalkyl carbenium ions amounts to -56.7 kJ/mol, while that towards tertiary intermediates amounts to -105.9 kJ/mol. This leads to a difference in stability of 49.2 kJ/mol between secondary and tertiary cycloalkyl carbenium ions, resulting in a higher concentration of the latter than the former. The protonation enthalpy towards secondary and tertiary alkyl carbenium ions were estimated to be -66.6 kJ/mol and -125.5 kJ/mol by Gaoping, et al.[26]Upon comparing the protonation enthalpy towards cyclic carbenium ions with that towards alkyl ones, it can be seen that the protonation enthalpy towards secondary or tertiary cyclic carbenium ions is very close to that towards secondary or tertiary alkyl carbenium ions.

The activation energies for PCP-isomerization of cyclic carbenium ions agree quite well with those reported by Quintana-Solórzano, et al.[22]. Furthermore, upon comparing PCP-isomerization of cyclic carbenium ions to those of alkyl carbenium ions, the activation energies for PCP-isomerization of cyclic carbenium ions obtained in this work are relatively higher than those of alkyl carbenium ions obtained in the catalytic cracking of acyclic hydrocarbons[22]. With respect to endocyclic β-scission, the activation energies estimated in this work fall in the range of 162—235 kJ/mol as reported by Quintana-Solórzano, et al.[22]

With respect to allylic cyclic carbenium ions, the activation energies for (de)protonation involving allylic species have significantly changed compared to those obtained by Quintana-Solórzano, et al.[22]The activation energies obtained in this work for pro_a(s) and pro_a(t) partially overlap with those obtained by Quintana-Solórzano, et al.[22], while the activation energies for dep_a(s) and dep_ a(t) obtained in this work are respectively higher and lower compared to the previously reported ones[22]. The more pronounced stability of allylic carbenium ions is well reflected in the difference in protonation enthalpies towards alkyl cyclic carbeninm ions and allylic cyclic carbenium ions. The protonation enthalpy towards secondary allylic cyclic carbenium ions is estimated at -89.7 kJ/mol, while that towards tertiary ones amounts to -84.0 kJ/mol. This minor difference in protonation enthalpy indicates that the allylic character dominates the type of carbon atom which is accepting the charge. It can be attributed to a strong resonance effect caused by the double bond and the positive charge in the allylic structure. The modelling results suggest that this effect is so intense that it can compensate for the difference in stabilities of secondary and tertiary cyclic carbenium ions.

With respect to hydride transfer reactions involving allylic carbenium ions, the activation energy for htr_a is very close to that obtained by Quintana-Solórzano, et al.[22], and it is much lower than that for htr_n, indicating that allylic cyclic carbenium ions are more easily formed than cyclic carbenium ions via hydride transfer reaction. Moreover, the activation energy for htr_c, incorporated in the SEMK model for the first time in this work, was found to be not only higher than that for htr_a, but even higher than that for htr_n. As it has been already anticipated previously, this indicates that the consumption of allylic carbenium ions via hydride transfer is much more difficult than the formation of allylic and cyclic carbenium ions via hydride transfer reactions.

Figure 3 shows the parity diagrams for the unconverted feed and main products, i.e., paraffins, olefins, cycloparaffins, cyclic olefins, and aromatics under various operating conditions. It can be seen that all these five types of hydrocarbons were well predicted by the enhanced SEMK model, particularly the paraffins and cycloparaffins. Compared to the previous implementation of the SEMK model[22], improvements were mainly exhibited in the simulation of benzene and cyclohexene on the one hand and that of 8-carbon-atom containing hydrocarbons on the other hand. While the improvement for the C6hydrocarbons could be attributed to the changes with respect to hydride transfer reactions involving allylic carbenium ions, that for the C8hydrocarbons can be attributed to the implementation of the thermodynamic consistency of cyclization and endocyclic β-scissions.

Based on the parity diagrams shown in Figure 3, it can be seen that the enhanced SEMK model is adequate in de-scribing the product distributions of the catalytic cracking of cycloparaffins admixed with olefins, and the enhancement to the previous SEMK model is successful.

Figure 3 Parity diagrams for the feedstock and various products of catalytic cracking of methylcyclohexane and 1-octene

5 Conclusions

The single-event microkinetic (SEMK) model that has been enhanced with respect to accounting for allylic carbenium ions and thermodynamic consistency in the ring opening reactions, is able to adequately describe the catalytic cracking of methylcyclohexane admixed with 1-octene over REY zeolite at industrially relevant temperature 693 K—753 K in the absence of coke formation. In particular the simulation of cyclic C6and C8species formation has significantly improved. Differences in carbenium ion stability depending on their secondary or tertiary type were pronounced in relation to acyclic carbenium ions as well as to cyclic carbenium ions, but were not pronounced in relation to allyllic ones. The resonance effect of the allylic structures dominates the stability of the carbenium ion as compared to the type of carbon atom which is accepting the charge.

Nomenclature

cyc——cyclization

dep_a——deprotonation of allylic cyclic carbenium ions

dep_n——deprotonation of cyclic carbenium ions

disp——disproportionation of aromatics

edβ——endocyclic β-scission

HS——hydride shift

HS_a——hydride shift forming allylic structures

HS_c——hydride shift breaking allylic structures

htr——all hydride transfer reactions

htr_a——hydride transfer forming allylic cyclic carbenium ions

htr_c——hydride transfer consuming allylic cyclic carbenium ions

htr_n——hydride transfer of cycloparaf fins

htr_o——hydride transfer of olefins yielding non-allylic olefinic carbenium ions

htr_ol——hydride transfer of ole fins yielding allylic ole finic carbenium ions

k——rate coef ficient [s-1] or [(s·Pa)-1]

p——primary carbenium ion

PCP_n——protonated cyclopropane intermediated isomerization of cycloparaf fins

pro_a——protonation of cyclic diole fins or aromatics

pro_n——protonation of cyclic ole fins

prsc_n——protolysis of cycloparaf fins

R——net production rate [mol/(kg·s)]

res——allylic resonance

s——secondary carbenium ion

SSQ——sum of squares

t——tertiary carbenium ion

Acknowledgements:The authors acknowledge financial support from the China Scholarship Council and the Long Term Structural Methusalem Funding by the Flemish Government.

Reference

[1] Stocker M. Gas Phase Catalysis by Zeolites[J]. Microporous and Mesoporous Materials, 2005, 82(3): 257-292

[2] Quintana-Solórzano R. Single-Event Microkinetics for Coking in Catalytic Cracking: Development and Application[D]. Ghent: Ghent University, 2007

[3] Feng W, Vynckier E, Froment G F. Single-event kinetics of catalytic cracking[J]. Industrial & Engineering Chemistry Research, 1993, 32(12): 2997-3005

[4] Corma A, Miguel P J, Orchilles A V, et al. Cracking of longchain alkyl aromatics on USY zeolite catalysts[J]. Journal of Catalysis, 1992, 135(1): 45-59

[5] Kotrel S, Kn?zinger H, Gates B C. The Haag–Dessau mechanism of protolytic cracking of alkanes[J]. Microporous and Mesoporous Materials, 2000, 35-36: 11-20

[6] Abbot J. Active sites and intermediates for isomerization and cracking of cyclohexane on HY[J]. Journal of Catalysis, 1990, 123(2): 383-395

[7] Corma A, Mocholi F, Orchilles V, et al. Methylcyclohexane and methylcyclohexene cracking over zeolite Y catalysts[J]. Applied Catalysis, 1991, 67(1): 307-324

[8] De La Puente G, Sedran U. Conversion of methylcyclopentane on rare earth exchanged Y zeolite FCC catalysts[J]. Applied Catalysis A: General, 1996, 144(1–2): 147-158

[9] Mostad H B, Riis T U, Ellestad O H. Shape selectivity in Y-zeolites: catalytic cracking of decalin-isomers in fixed bed micro reactors[J]. Applied Catalysis, 1990, 58(1): 105-117

[10] Sousa-Aguiar E F, Mota C J A, Valle M L M, et al. Catalytic cracking of decalin isomers over ReHY-zeolites with different crystallite sizes[J]. Journal of Molecular Catalysis A: Chemical, 1996, 104(3): 267-271

[11] Corma A, Gonzalez-Alfaro V, Orchilles A V. Decalin and tetralin as probe molecules for cracking and hydrotreating the light cycle oil[J]. Journal of Catalysis, 2001, 200(1): 34-44

[12] Kubi?ka D, Kumar N, M?ki-Arvela P, et al. Ring opening of decalin over zeolites: I. Activity and selectivity of protonform zeolites[J]. Journal of Catalysis, 2004, 222(1): 65-79

[13] De La Puente G, Sedran U. Evaluation of hydrogen transfer in FCC catalysts. A new approach for cyclohexene as a test reactant[J]. Chemical Engineering Science, 2000, 55(4): 759-765

[14] Cerqueira H S, Mihindou-Koumba P C, Magnoux P, et al. Methylcyclohexane transformation over HFAU, HBEA, and HMFI zeolites: I. Reaction scheme and mechanisms[J]. Industrial & Engineering Chemistry Research, 2001, 40(4): 1032-1041

[15] Al-Sabawi M, De Lasa H. Kinetic modeling of catalytic conversion of methylcyclohexane over USY zeolites: adsorption and reaction phenomena[J]. AIChE Journal, 2009, 55(6): 1538-1558

[16] Marques J P, Gener I, Lopes J M, et al. Methylcyclohexane transformation over dealuminated HBEA samples: Mechanisms and active sites[J]. Applied Catalysis A-General, 2006, 301(1): 96-105

[17] Watson B A, Klein M T, Harding R H. Catalytic cracking of alkylcyclohexanes: Modeling the reaction pathways and mechanisms[J]. International Journal of Chemical Kinetics, 1997, 29(7): 545-560

[18] Liguras D K, Allen D T. Structural models for catalytic cracking. 1. Model-compound reactions[J]. Industrial & Engineering Chemistry Research, 1989, 28(6): 665-673

[19] Quann R J, Jaffe S B. Structure-oriented lumping - describing the chemistry of complex hydrocarbon mixtures[J]. Industrial & Engineering Chemistry Research, 1992, 31(11): 2483-2497

[20] Mcdermott J B, Libanati C, Lamarca C, et al. Quantitative use of model compound information: Monte Carlo simulation of the reactions of complex macromolecules[J]. Industrial & Engineering Chemistry Research, 1990, 29(1): 22-29

[21] Baltanas M A, Vanraemdonck K K, Froment G F, et al. Fundamental kinetic modeling of hydroisomerization and hydrocracking on noble-metal-loaded faujasites. 1. Rate parameters for hydroisomerization[J]. Industrial & Engineering Chemistry Research, 1989, 28(7): 899-910

[22] Quintana-Solórzano R, Thybaut J W, Marin G B. A singleevent microkinetic analysis of the catalytic cracking of (cyclo)alkanes on an equilibrium catalyst in the absence of coke formation[J]. Chemical Engineering Science, 2007,62(18–20): 5033-5038

[23] Quintana-Solórzano R, Thybaut J W, Marin G B. Catalytic cracking and coking of (cyclo)alkane/1-octene mixtures on an equilibrium catalyst[J]. Applied Catalysis A: General, 2006, 314(2): 184-199

[24] Yaluris G, Rekoske J E, Aparicio L M, et al. Isobutane cracking over Y-zeolites: I. Development of a kineticmodel[J]. Journal of Catalysis, 1995, 153(1): 54-64

[25] Martens G G, Thybaut J W, Marin G B. Single-event rate parameters for the hydrocracking of cycloalkanes on Pt/ USY zeolites[J]. Industrial & Engineering Chemistry Research, 2001, 40(8): 1832-1844

[26] Xue Gaoping, Thyabut J W, Weng Huixin, et al. Single-Event Microkinetic (SEMK) assessment of the catalytic cracking of alkanes admixed with alkenes[C]. Accepted, the 23 rd International Symposium on Chemical Reaction Engineering (ISCRE23), 2014

[27] Netlib. http://www.netlib.org

[28] Rosenbrock H H. An automatic method for finding the greatest or least value of a function[J]. Computer Journal, 1960, 3(3): 175-184

[29] Marquardt D W. An algorithm for least-squares estimation of nonlinear parameters[J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431-441

[30] Dewachtere N V, Santaella F, Froment G F. Application of a single-event kinetic model in the simulation of an industrial riser reactor for the catalytic cracking of vacuum gas oil[J]. Chemical Engineering Science, 1999, 54(15-16): 3653-3660

[31] Moustafa T M, Froment G F. Kinetic modeling of coke formation and deactivation in the catalytic cracking of vacuum gas oil[J]. Industrial & Engineering Chemistry Research, 2003, 42(1): 14-25

[32] Corma A, Wojciechowski B W. The chemistry of catalytic cracking[J]. Catalysis Reviews-Science and Engineering, 1985, 27(1): 29-150

[33] Corma A, Miguel P J, Orchilles a V. The role of reaction temperature and cracking catalyst characteristics in determining the relative rates of protolytic cracking, chain propagation, and hydrogen-transfer[J]. Journal of Catalysis, 1994, 145(1): 171-180

Recieved date: 2013-10-22; Accepted date: 2013-12-30.

Weng Huixin, Telephone: +86-21-64252816; E-mail: hxweng@ecust.edu.cn.