CAO Xiao-shuang,XU Shao-yuan

(1.School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China;2.Department of Mathematics and Statistics,Hanshan Normal University,Chaozhou 521041,China)

Some Notes on G-cone Metric Spaces

CAO Xiao-shuang1,XU Shao-yuan2

(1.School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China;2.Department of Mathematics and Statistics,Hanshan Normal University,Chaozhou 521041,China)

In this paper,we introduce a G metric on the G-cone metric space and then prove that a complete G-cone metric space is always a complete G metric space and verify that a contractive mapping on the G-cone metric space is a contractive mapping on the G metric space.At last,we also give a new way to obtain the unique f i xed point on G-cone metric space.

G-cone metric space;G metric;contractive mapping

§1.Introduction

In last two decades,many authors focused on f i xed point theory for contractive or generalized contractive mappings in abstract spaces(see[1-19]).To overcome fundamental f l aws in Dhage’s theory of generalized metric space[23].Mustafa and Sims[15]introduced a more appropriate generalization of metric space,that is,G metric space.Then,a concept of G-cone metric space,which we can consider to be the generalization of G metric space,was introduced by replacing the set of real numbers by an ordered Banach space[4].What’s more,in[5-9, 11-13],the authors extended some f i xed point theorems on metric space to cone metric space.

In this paper,we introduce a G metric D on the G-cone metric space(X,d)and due to the relevant results[13],we point out that a complete G-cone metric space is always a complete G metric space and show that contractive mappings on a G-cone metric space(X,d)are contractive on the G metric space(X,D).Besides,at last,we also give a new way to obtain the unique f i xed point on G-cone metric space.

§2.Preliminaries

The following def i nitions and results will be needed in the sequel.

Let E be a real Banach space.A subset P of E is called a cone if and only if

(a)P is closed,non empty and P/={θ};

(b)a,b∈?,a,b≥0,x,y∈P?ax+by∈P;More generally,if a,b,c∈?,a,b,c≥0, x,y,z∈P?ax+by+cz∈P;

(c)P∩(?P)={θ}.

Given a cone P?E,we def i ne a partial ordering≤with respect to P by x≤y if and only if y?x∈P,while x?y stands for y?x∈intP(interior of P).

Def i nition 2.1[4]Let X be a nonempty set.Suppose a mapping G:X×X×X→E satisf i es

(G1)G(x,y,z)=0 if x=y=z;

(G2)0＜G(x,x,y),whenever x/=y,for all x,y∈X;

(G3)G(x,x,y)≤G(x,y,z),whenever y/=z;

(G4)G(x,y,z)=G(x,z,y)=G(y,x,z)=···(symmetric in all three variables);

(G5)G(x,y,z)≤G(x,a,a)+G(a,y,z),for all x,y,z,a∈X.

Then G is called a generalized cone metric on X and X is called a generalized cone metric space or more specif i cally a G-cone metric space.

Remark 2.2(1)It is clear that if G(x,y,z)=0,then x=y=z.That is,G(x,y,z)=0 if and only if x=y=z.

(2)In Def i nition 2.1,if we replace G:X×X×X→E by G:X×X×X→R,then G cone metric space is reduced to G metric space.

Def i nition 2.3[15]A G metric space(X,G)is symmetric if

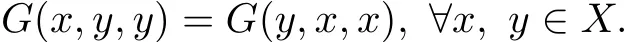
Lemma 2.4[15]Let(X,G)be a G metric space and def i ne dG:X×X→E by

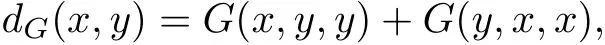
then(X,dG)is a metric space.

It can be noted that G(x,y,y)≤dG(x,y).If(X,G)is a symmetric G metric space,then

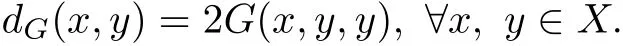
Def i nition 2.5[4]Let X be a G-cone metric space and{xn}be a sequence in X.We say that{xn}is

(a)Cauchy sequence if for every c∈E with 0?c,there is N such that for all n,m,l＞N,G(xn,xm,xl)?c.

(b)Convergent sequence if for every c in E with 0?c,there is N such that for all m,n＞N,G(xm,xn,x)?c for some f i xed x in X.Here x is called the limit of a sequence {xn}and is denoted by=x or xn→x as n→∞.

A G-cone metric space X is said to be complete if every Cauchy sequence in X is convergent in X.

Lemma 2.6[15]Let X be a G metric space.If we suppose that{xn},{yn}and{zn}are sequences in X such that xn→x,yn→y and zn→z,then G(xm,yn,zl)→G(x,y,z)as m,n,l→∞(G metric is jointly continuous).

Lemma 2.7[15]Let X be a G metric space.Then for a sequence{xn}?X and a point x∈X,the following statements are equivalent

(i){xn}is convergent to x;

(ii)G(xn,xn,x)→0 as n→∞;

(iii)G(xn,x,x)→0 as n→∞;

(iv)G(xm,xn,x)→0 as m,n→∞.

Lemma 2.8[1]Let(X,d)be a complete metric space.Suppose the mapping T:X→X satisf i es the contractive condition

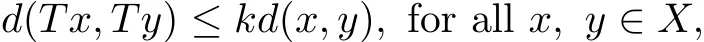
where k∈[0,1)is a constant.Then T has a unique f i xed point in X.And for any x∈X, iterative sequence{Tnx}converges to the f i xed point.

Lemma 2.9[16]Let(X,G)be a complete G-metric space and T:X→X be a mapping satisfying the following condition for all x,y,z∈X

where k∈[0,1).Then T has a unique f i xed point.

§3.Main Results

Theorem 3.1Let(X,d)be a G-cone metric space,then

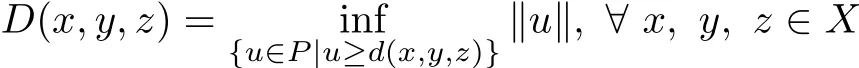
is a G metric on X.

Proof(G1)and(G2)are obvious.

(G3)Let x,y,z∈X,by the def i nition of G-cone metric,we have

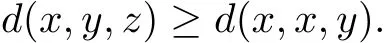
Noting that

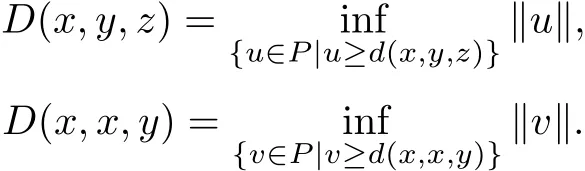
Then for arbitrary u,v∈P,suppose that u≥d(x,y,z),v≥d(x,x,y),we see

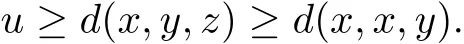
Obviously,we can get D(x,x,y)≤‖u‖,which implies

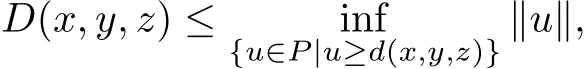
that is,

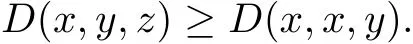
(G4)By the chain of equalities d(x,y,z)=d(x,z,y)=d(y,z,x)=···,we have

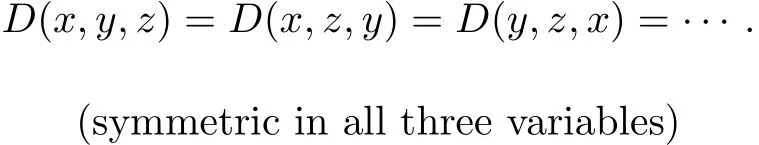
(G5)Let x,y,z∈X,by the def i nition of G-cone metric,we have

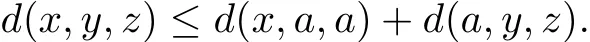
Noting that

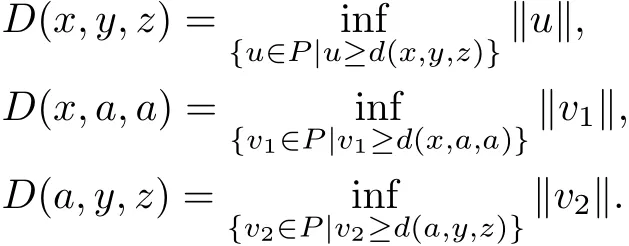
Then for arbitrary v1,v2∈P,suppose that v1≥d(x,a,a),v2≥d(a,y,z),we see

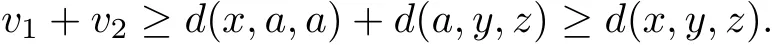
Obviously,we can get D(x,y,z)≤‖v1+v2‖,which implies

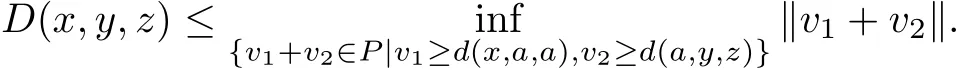
Considering

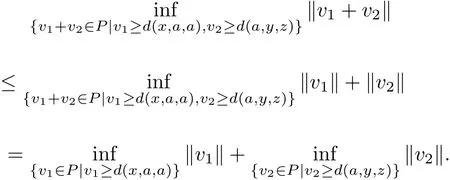
Therefore,we obtain

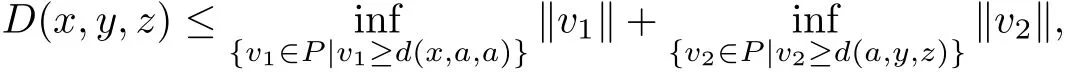
that is,

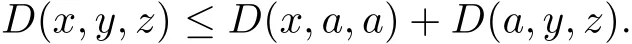
(G1)～(G5)show that D is a G metric on X.

(2){xn}is a Cauchy sequence on the G-cone metric space(X,d)if and only if{xn}is a Cauchy sequence on the G metric space(X,D).

(3)The G-cone metric space(X,d)is complete if and only if the G metric space(X,D)is complete.

Proof(1)Suppose that{xn}is convergent to x on the G-cone metric space(X,d).For each ε＞0,c?0,then

?0.Then for each c∈E with c?θ,there exists n0such that

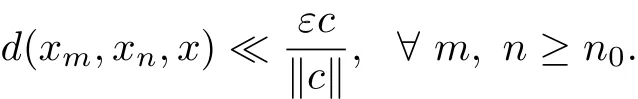
Therefore,we have

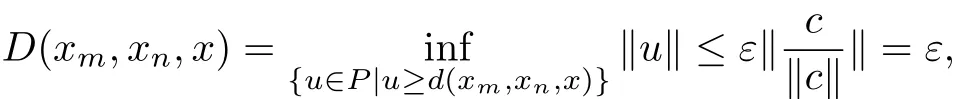
which implies that

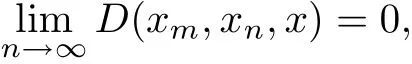
that is,{xn}is convergent to x on the G metric space(X,D).

Conversely,suppose that{xn}is convergent to x on the G metric spaces(X,D).For each c?0,there exists ε＞0 such that c+B(0,ε)?P.For this ε,there exists n0such that

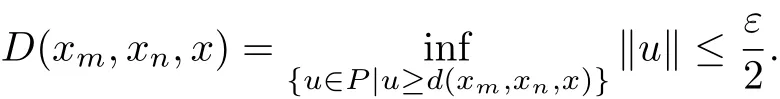
Then,there exists v∈P,‖v‖≤ε such that d(xm,xn,x)≤v.Noting that v?c,we see

It is obvious that we can get d(xm,xn,x)?c,which implies that{xn}is convergent to x on the G-cone metric spaces(X,d).

(2)Suppose that{xn}is a Cauchy sequence on the G-cone metric spaces(X,d).For each ε＞0,if c?θ,then?θ.Then for each c∈E with c?θ,there exists n0such that

Therefore,we have

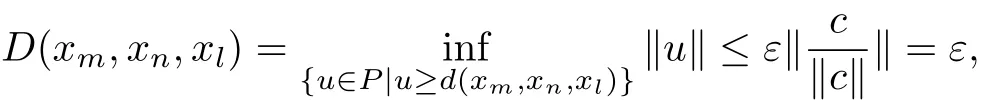
which shows that{xn}is a Cauchy sequence on the G metric spaces(X,D).

Conversely,suppose that{xn}is a Cauchy sequence on the G metric spaces(X,D).Then we get

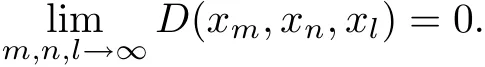
For each c?θ,there exists ε＞0 such that c+B(0,ε)?P.For this ε,there exists n0such that

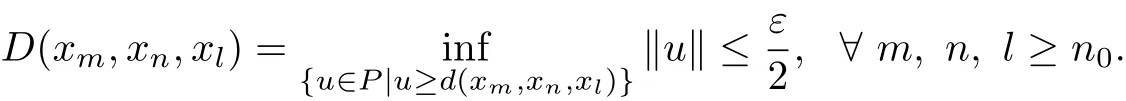
Then,there exists v∈P,‖v‖≤ε,such that d(xm,xn,xl)≤v.Noting that v?c,we have

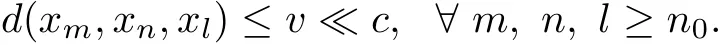
It is obvious that we can get d(xm,xn,xl)?c,which shows that{xn}is a Cauchy sequence on the G-cone metric spaces(X,d).

(3)It is a direct consequence of(1)and(2).

As a consequence of Theorem 3.2,we easily get the following.

Corollary 3.3(X,d)is a sequentially compact G-cone metric space if and only if(X,D) is a compact G metric space.

Another result of this paper says that a contractive mapping on G-cone metric space is always contractive on G metric space.More precisely,we have

Theorem 3.4Let(X,d)be a complete G-cone metric space.If T:X→X satisf i es the contractive condition

where k∈[0,1)is a constant,then T is a contractive mapping on(X,D),i.e.,

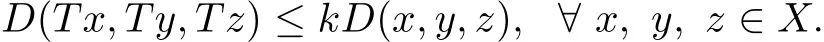
Hence,T has a unique f i xed point in X.

ProofLet v∈P,suppose that v≥d(x,y,z),then kv≥d(Tx,Ty,Tz),which implies that

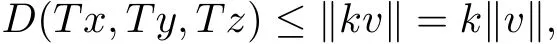
we get

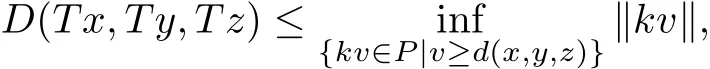
that is,

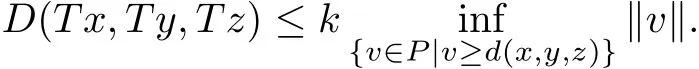
Therefore,we have

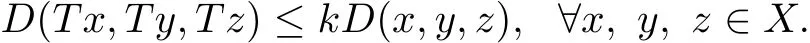
Corollary 3.5Let(X,d)be a complete G-cone metric space and T:X→X be a mapping satisfying one of the following conditions

(1)d(Tx,Ty,Tz)≤λ1d(x,y,z)+λ2d(x,Tx,Tx)+λ3d(y,Ty,Ty)+λ4d(z,Tz,Tz);

(2)d(Tx,Ty,Tz)≤λ1d(x,y,z)+λ2d(x,x,Tx)+λ3d(y,y,Ty)+λ4d(z,z,Tz),for all x,y,z∈X,where λ1+λ2+λ3+λ4∈[0,1),then T is a contractive mapping on(X,D).

That is,

(3)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,Tx,Tx)+λ3D(y,Ty,Ty)+λ4D(z,Tz,Tz);

(4)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,x,Tx)+λ3D(y,y,Ty)+λ4D(z,z,Tz).

Hence T has a unique f i xed point in X.

ProofLet v1,v2,v3,v4∈P,suppose that v1≥d(x,y,z),v2≥d(x,Tx,Tx),v3≥d(x,Ty,Ty),v4≥d(z,Tz,Tz),then we have

which implies

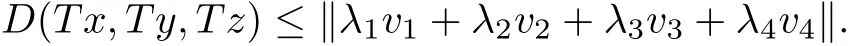
Therefore,we easily get

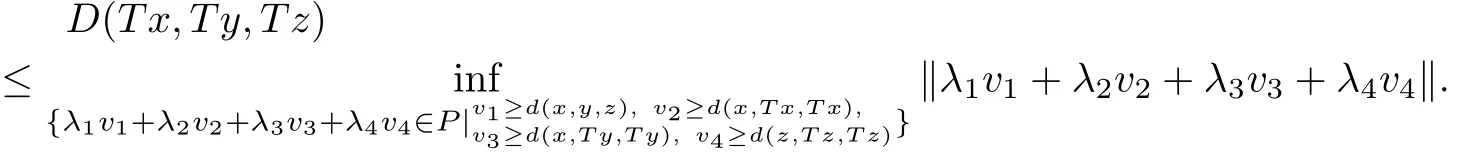
Noting that

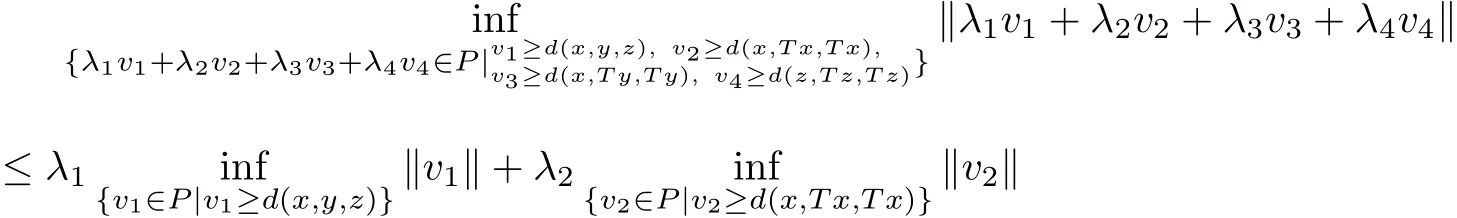
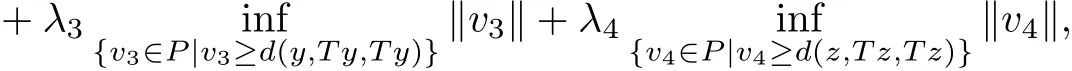
we have

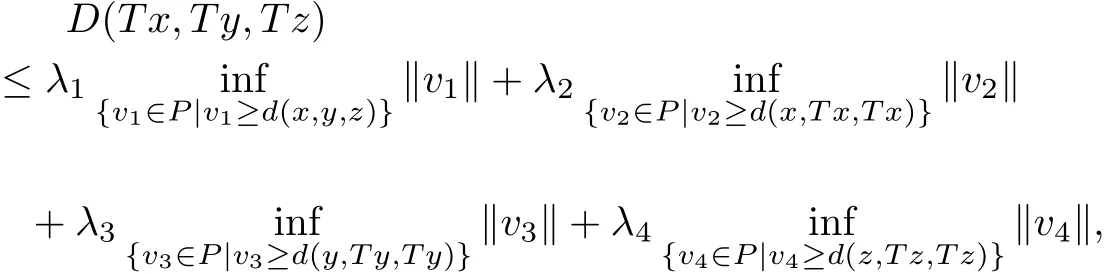
that is,?x,y,z∈X,we obtain

D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,Tx,Tx)+λ3D(y,Ty,Ty)+λ4D(z,Tz,Tz).

Similarly,if T satisf i es condition(2),the result can be proved in the same way.

Theorem 3.6Let(X,D)be a complete G metric space and T:X→X be a mapping satisfying one of the following conditions

(3)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,Tx,Tx)+λ3D(y,Ty,Ty)+λ4D(z,Tz,Tz);

(4)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,x,Tx)+λ3D(y,y,Ty)+λ4D(z,z,Tz),for all x,y,z∈X,where λ1+λ2+λ3+λ4∈[0,1),then T has a unique f i xed point in X.

ProofSuppose that T satisf i es condition(3),then for all x,y∈X,we have

(5)D(Tx,Ty,Ty)≤λ1D(x,y,y)+λ2D(x,Tx,Tx)+(λ3+λ4)D(y,Ty,Ty);

(6)D(Ty,Tx,Tx)≤λ1D(y,x,x)+λ2D(y,Ty,Ty)+(λ3+λ4)D(x,Tx,Tx). If(X,D)is symmetric,then by def i nition of metric(X,DG),we can get

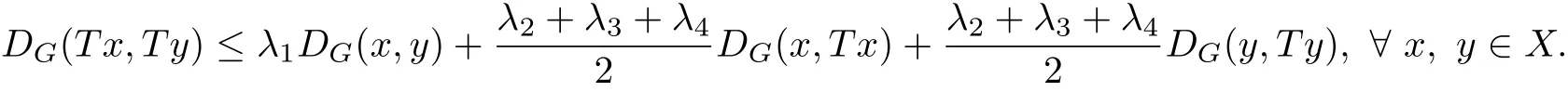
Since λ1+λ2+λ3+λ4∈[0,1),then the existence and uniqueness of the f i xed point follows from well-known theorem on metric space(X,DG).

However,if(X,D)is not asymmetric.Let x0∈X be an arbitrary point,and def i ne the sequence{xn}by xn=Txn?1.

By condition(3),we have

D(xn,xn+1,xn+1)≤λ1D(xn?1,xn,xn)+λ2D(xn?1,xn,xn)+(λ3+λ4)D(xn,xn+1,xn+1), that is,

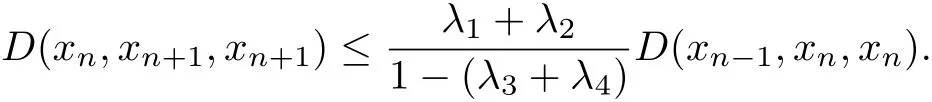
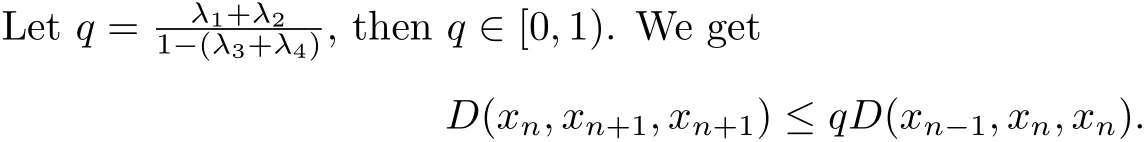
Continuing in the same argument,we will get

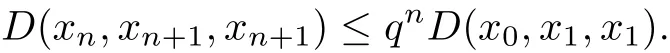
Moreover,for all m,n∈?,m＞n,we have by rectangle inequality that

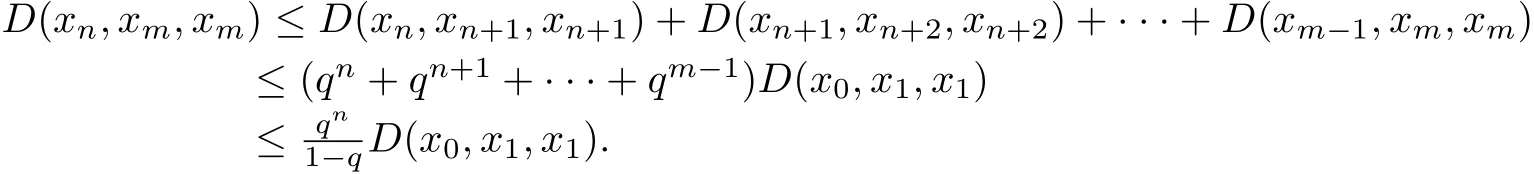
Taking the limit as n→∞,then for all ε＞0,there exists a N＞0 such that for all n＞N

which implies that D(xn,xm,xm)≤ε.

Therefore,{xn}is a Cauchy sequence.Due to the completeness of(X,D),there exists u∈X such that xnis convergent to u.Suppose that Tu/=u,then we obtain

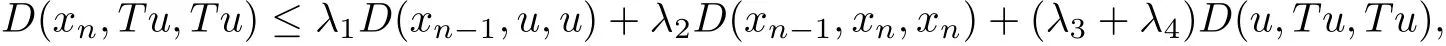
taking the limit as n→∞and using the fact that D is jointly continuous,we get

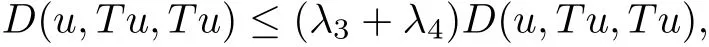
which implies that u=Tu.

To prove uniqueness,suppose that u/=v such that Tv=v,we have

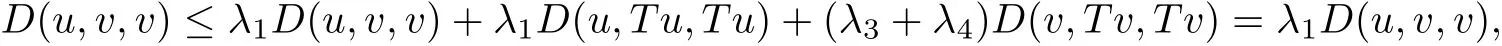
which implies that u=v.

Similarly,if T satisf i es condition(4),the result can be proved in the same way.Therefore, T has a unique f i xed point.

Remark 3.7If(X,D)is not asymmetric.By def i nition of metric DG,we can getThen the metric condition gives no information about this mapping sinceneed not be less than 1.Therefore we choose to use G metric to prove it.

Theorem 3.8Let(X,d)be a complete G-cone metric space and T:X→X be a mapping satisfying one of the following conditions

(1)d(Tx,Ty,Tz)≤λ1d(x,y,z)+λ2d(x,Tx,Tx)+λ3d(y,Ty,Ty)+λ4d(z,Tz,Tz);

(2)d(Tx,Ty,Tz)≤λ1d(x,y,z)+λ2d(x,x,Tx)+λ3d(y,y,Ty)+λ4d(z,z,Tz),for all x,y,z∈X,where λ1+λ2+λ3+λ4∈[0,1),then T has a unique f i xed point in X.

ProofLet D:X×X×X→[0,+∞)be def i ned byz∈X,then Theorem 3.1 shows that D(x,y,z)is a G metric space on X.Also,by Corollary 3.5,in G metric space(X,D)the mapping T satisf i es the following conditions

(3)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,Tx,Tx)+λ3D(y,Ty,Ty)+λ4D(z,Tz,Tz);

(4)D(Tx,Ty,Tz)≤λ1D(x,y,z)+λ2D(x,x,Tx)+λ3D(y,y,Ty)+λ4D(z,z,Tz)for all x,y,z∈X,where λ1+λ2+λ3+λ4∈[0,1).This ensures that T satisf i es the assumption of Theorem 3.6,which implies that T has a unique f i xed point in X.

[1]BANACH S.Sur les oprations dans les ensembles abstraits et leur application aux quations intgrales[J]. Fundam Math,1922,3:133-181.

[2]DHAGE B C.Gneneralized metric spaces and mapping with f i xed point[J].Bull Calcutta Math Soc,1992, 84:329-336.

[3]DHAGE B C.On contunity of mapping in D-metric spaces[J].Bulletin of the Calcutta Mathematical Society, 1994,86:503-508.

[4]BEG I,ABBAS M,NAZIR T.Gneneralized cone metric spaces[J].J Nonlinear Sci Appl,2010,3:21-31.

[5]RAO K P R,LAKSHMI K B,RAJU V C C.A unique common f i xed point theorem for three mappings in G-cone metric spaces[J].The Journal of Mathematics and Computer Science/TJMCS,2012,4:585-590.

[6]HUANG Long-guang,ZHANG Xian.Cone metric spaces and f i xed point theorems of contractive mappings[J].J Math Anal Appl,2007,332:1468-1476.

[7]ASGARI M S,ABBASBIGI Z.Generalizations of the Suzuki and Kannan f i xed point theorems in G-cone metric spaces[J].Anal Theory Appl,2012,28:248-262.

[8]OZTURK M,BASARR M.On some coincidence and common f i xed point theorems in G-cone metric spaces[J].Thai Journal of Mathematics,2011,9:647-657.

[9]VARGHESE P G,DERSANAMBIKA K S.Fixed point theorems on complete G-cone metric space[J].R J P A,2011,1:256-261.

[10]MOHANTA S K.Some f i xed point theorems in G-metric spaces[J].An S Univ O C,2012,20:285-306.

[11]MOHANTA S K.Common f i xed points for mappings satisfying ? and F-maps in G-cone metric spaces[J]. Bulletin of Mathematical Analysis and Applications,2012,4:133-147.

[12]REZAPOUR S,HAMLBARANI R.Some notes on the paper“Cone metric spaces and f i xed point theorems of contractive mappings”[J].J Math Anal Appl,2008,345:719-724.

[13]FENG Yu-qing,MAO Wei.The equivalence of cone metric spaces and metric spaces[J].Fixed Point Theory, 2010,11:259-264.

[14]MUSTAFA Z.Fixed point results on complete G-metric spaces[J].Stud Sci Math Hungar,2011,48:304-319.

[15]MUSTAFA Z,SIMS B.A new approach to gneneralized metric spaces[J].J Nonlinear and Convex Anal, 2006,7:289-297.

[16]MUSTAFA Z.A New Structure for Generalized Metric Spaces with Applications to Fixed Point Theory[D]. Australia:the University of Newcastle,2005.

[17]WANG Yun-jie,ZHU Jiang.Common f i xed points under contractive conditions in cone metric spaces[J]. Chinese Quarterly Journal of Mathematics,2013,28(1):47-52.

[18]WEN Kai-ting.A new browder f i xed point theorem in noncompact hyperconvex metric spaces and its applications to section questions and intersection questions[J].Chinese Quarterly Journal of Mathematics, 2009,24(1):112-116.

[19]WU Jian-rong,LIU Hai-yan.Common f i xed point theorems for sequences of-type contraction set-valued mappings[J].Chinese Quarterly Journal of Mathematics,2009,24(4):504-510.

tion:47H10,54H25

1002–0462(2014)04–0602–10

date:2013–08–06

Supported by the Natural Science Foundation of Hubei Province Education Department (Q20132505);SupportedbythePhDStart-upFundofHanshanNormalUniversityofGuangdong Province(QD20110920)

Biographies:CAO Xiao-shuang(1988-),female,native of Zhongxiang,Hubei,a postgraduate of Hubei Normal University,engages in nonlinear analysis;XU Shao-yuan(1964-),male,native of Wuhan,Hubei,a professor of Hanshan Normal University,engages in nonlinear analysis(corresponding author).

CLC number:O177.91Document code:A