A Kind of Identities for Products Reciprocals of q-binomial Coefficients
YANG Ji-zhen,WANG Yun-peng
(1.Department of Mathematics,Luoyang Normal College,Luoyang 471022,China;2.Department of Mathematics and Physical,Luoyang Institute of Science and Technology,Luoyang 471023,China)
A Kind of Identities for Products Reciprocals of q-binomial Coefficients
YANG Ji-zhen1,WANG Yun-peng2
(1.Department of Mathematics,Luoyang Normal College,Luoyang 471022,China;2.Department of Mathematics and Physical,Luoyang Institute of Science and Technology,Luoyang 471023,China)
The purpose of this paper is to establish some identities with products of q-Hermite polynomials,q-ultraspherical polynomials and reciprocals of q-binomial coefficients.
q-gamma function;q-beta function;q-integral;q-binomial coefficients
§1.Introduction
Let 0<q<1,q-gamma function Γq(x)is def i ned by

It is easy to see that

The generalized q-binomial coefficient is def i ned by
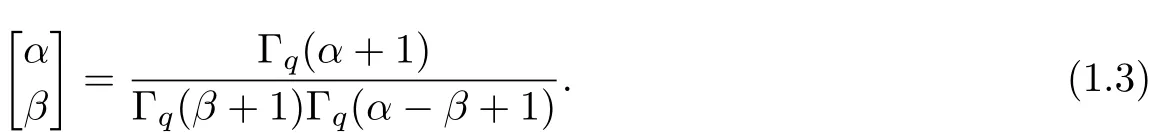
The q-Beta function is def i ned by

Thomae and Jackson introduced the q-intergral
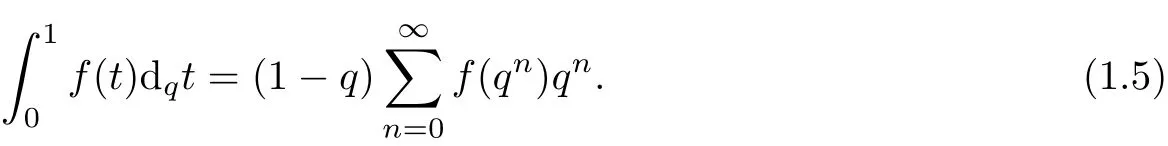
Then
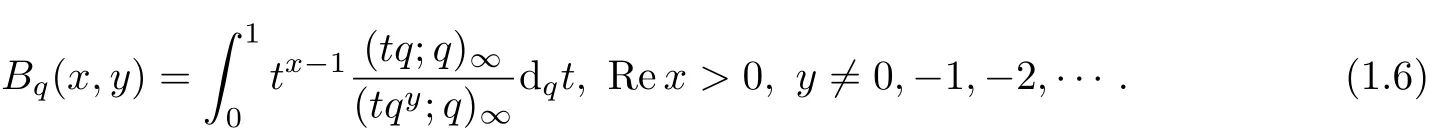
The details of above content,see[1,pages 20-24].
In[2-4],the integral representations and closed form representations for products reciprocals of binomial coefficients were discussed.The purpose of this paper is to get some identities with products of q-Hermite polynomials,q-ultraspherical polynomials and reciprocals of q-binomial coefficients.
§2.Main Results and Their Proofs
Theorem 1Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|···<1.Then

ProofApplying(1.1)~(1.6),we have

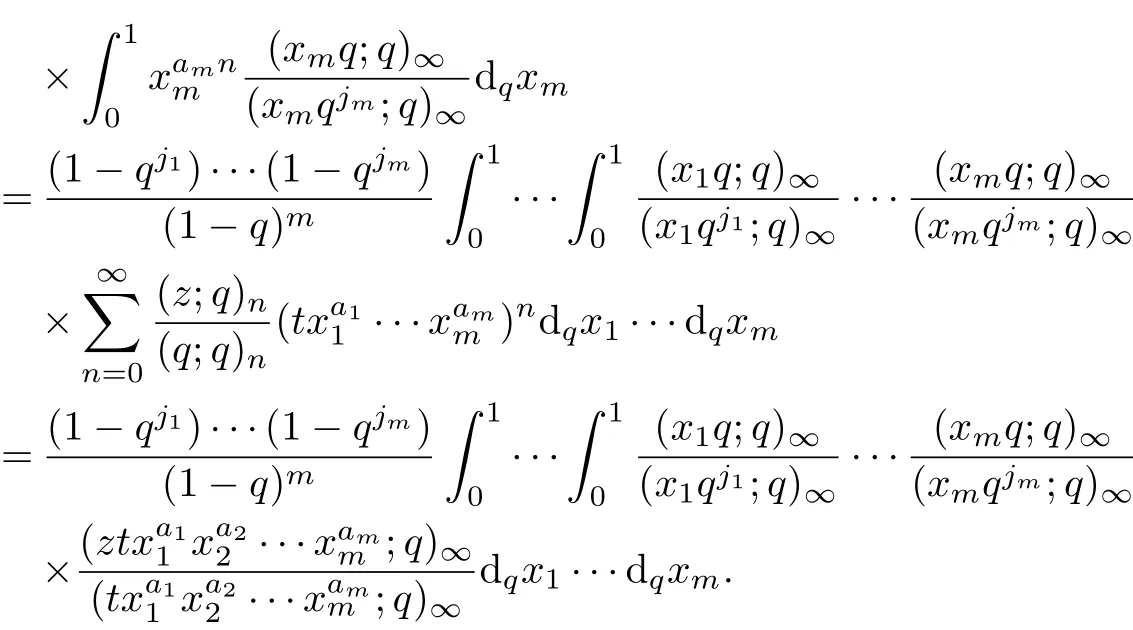
The proof of the theorem is completed.
If we take z→q and q→1 in Theorem 0.1,we can get the following identity. Corollary 1Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1
1···xamm|<1.Then

Let m=1 in Corollary 1,we can get the following identity.
Corollary 2Let a be real numbers,j≥0 and|txa|<1.Then
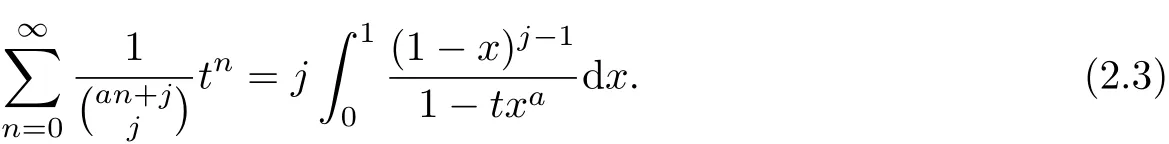
We can also obtain another result.
Theorem 2Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|<1. Then
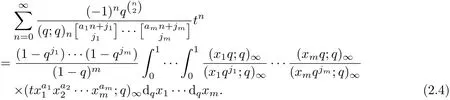
ProofApplying(1.1)~(1.6),we have
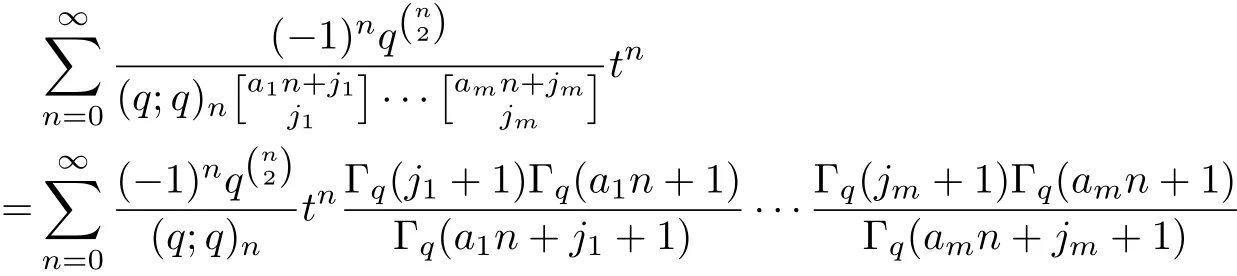
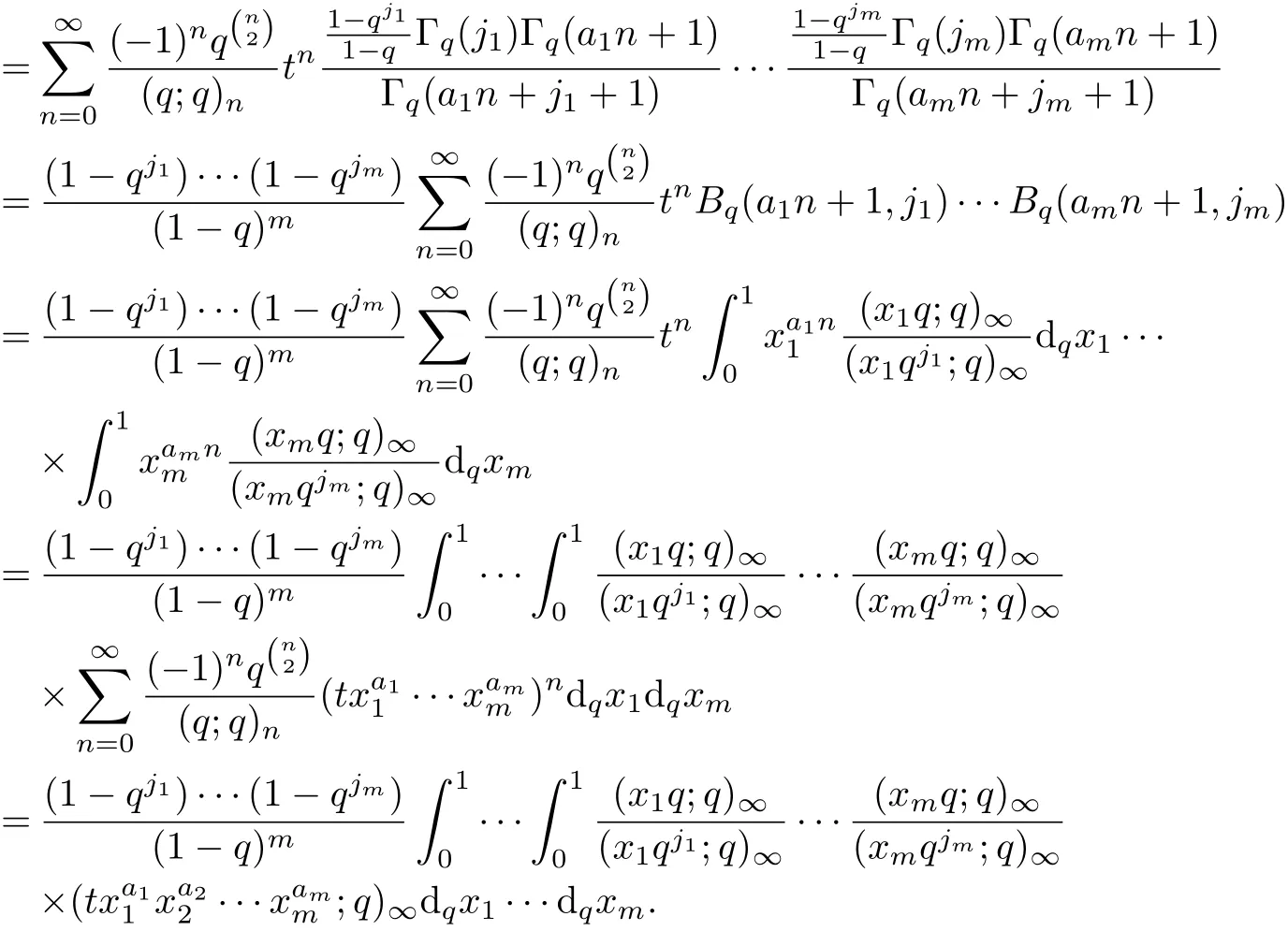
The proof of Theorem 2 is completed.
The continuous q-Hermite polynomials[1]are def i ned by
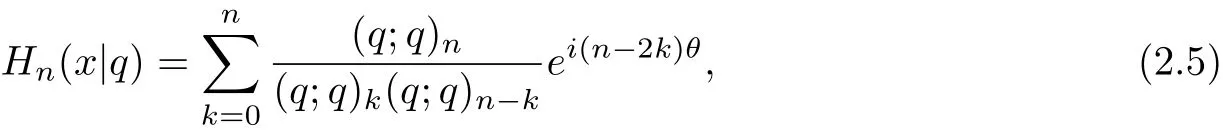
where x=cosθ.
By the excise 1.28 of[1]
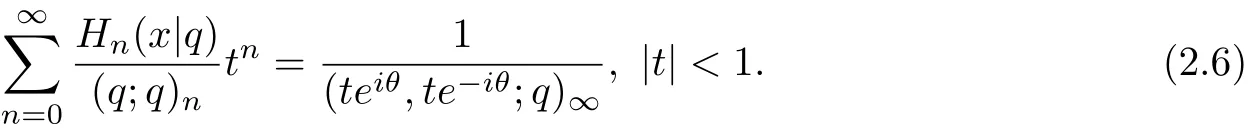
We can obtain the following identity.
Theorem 3Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|<1. Then
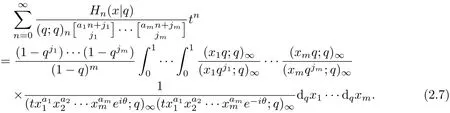
ProofBy equation(2.6),and using the same method in Theorem 1 and Theorem 2,we can get equation(2.7).
The continuous q-ultraspherical polynomials[1]are def i ned by
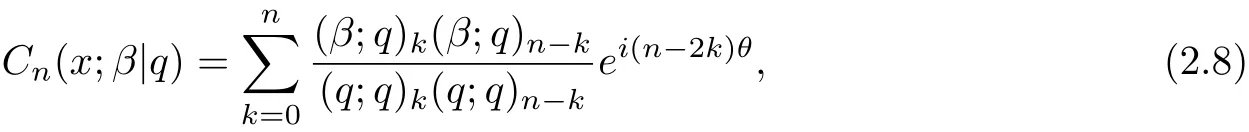
where x=cosθ.
By the excise 1.29 of[1]
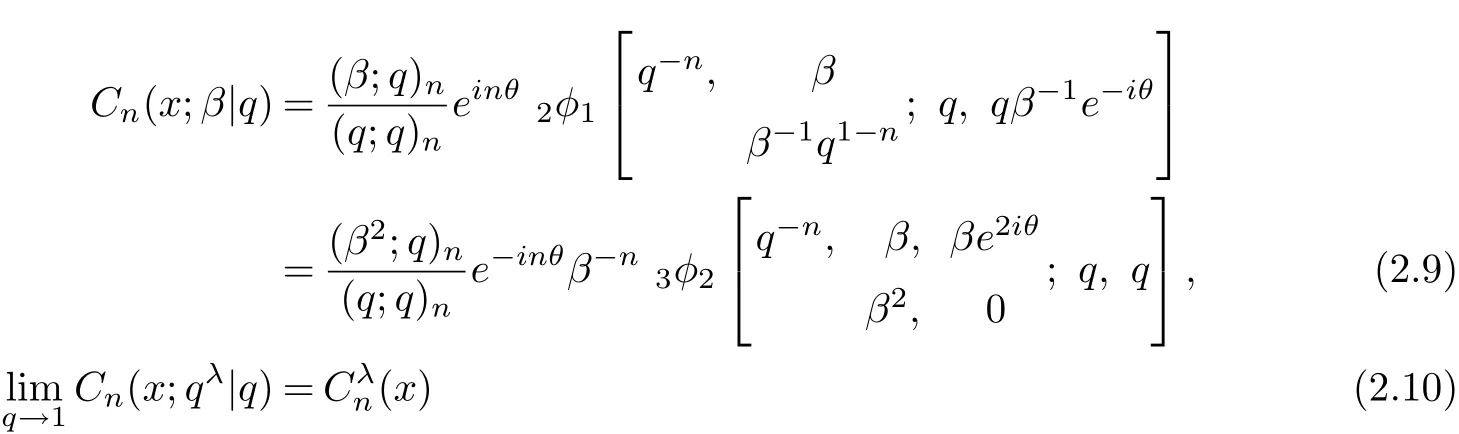
and
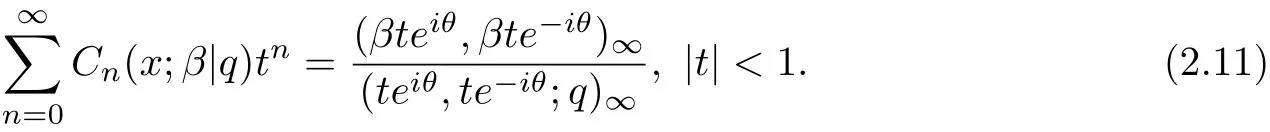
We can obtain the following identity.
Theorem 4Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|<1.Then
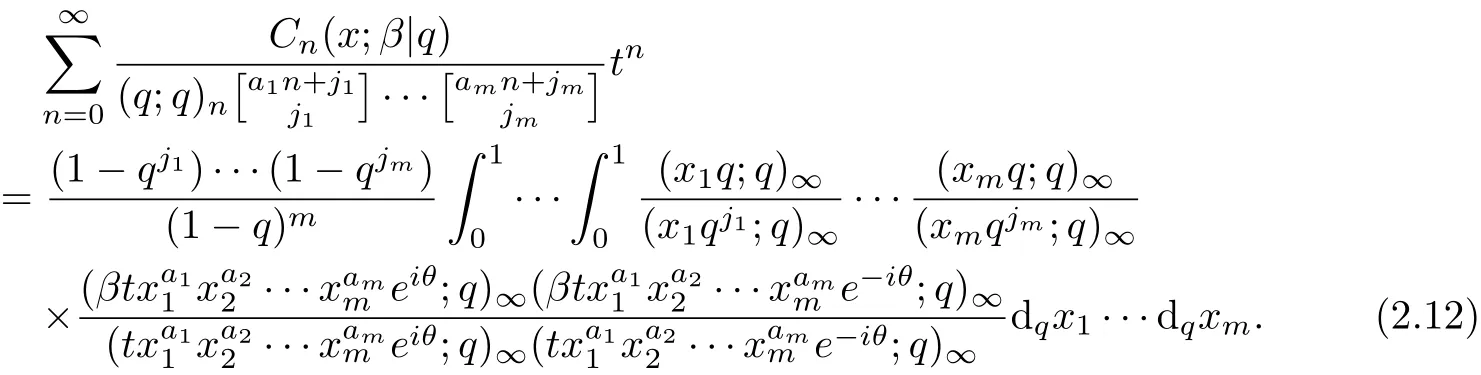
ProofSimilarly to Theorem 3,we can get the theorem.
§3.Summation Rormula Involving q-harmonic Numbers
The q-harmonic numbers are def i ned by

The generalization q-harmonic numbers can be def i ned by
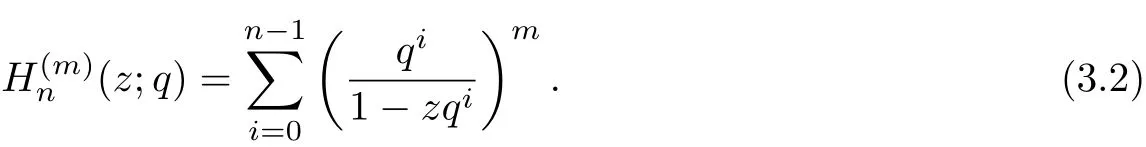
Observed that,let m=1 in the above identity,then
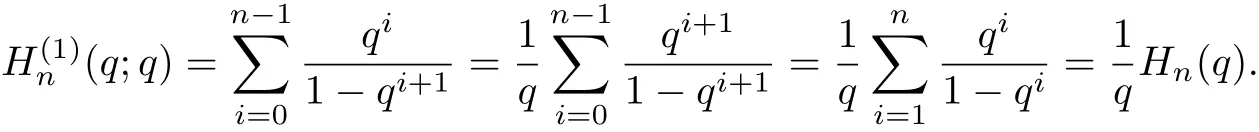
Dif f erentiating the identity of Theorem 1 with respect to the variable z,we can get the following identity.
Theorem 5Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1
1···xam
m|<1.Then
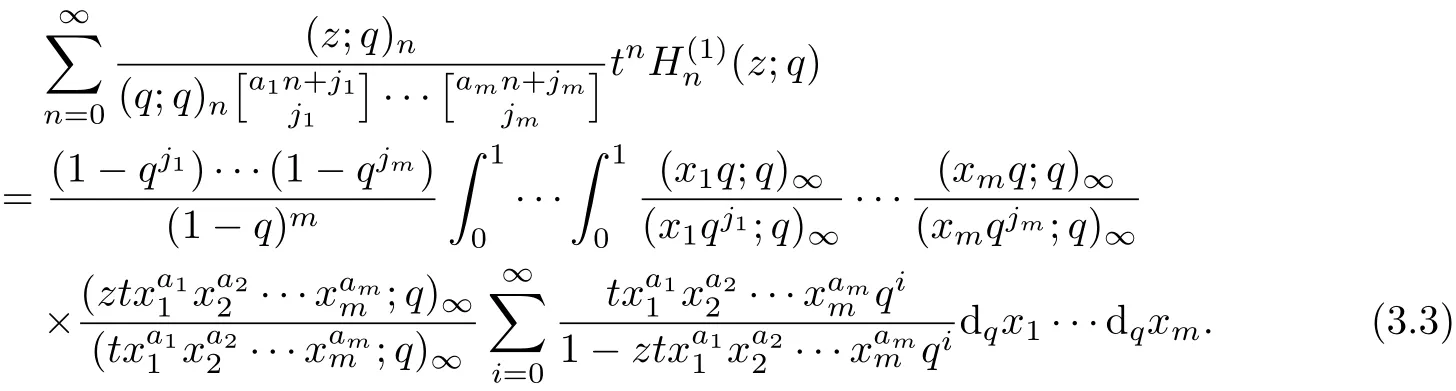
ProofSince(z;q)n=(1?z)(1?zq)···(1?zqn?1),then
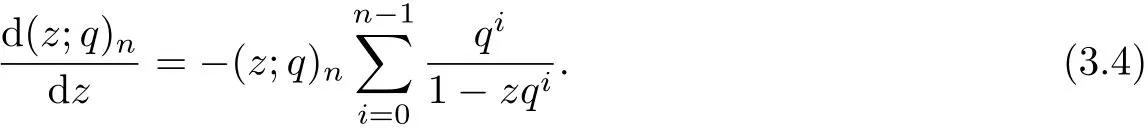
By the expansion of
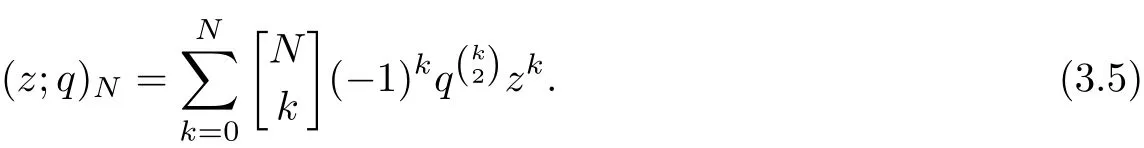
Dif f erentiating the equation(3.5)with respect to the variable z,we have

Let N→∞in the above identity,we get
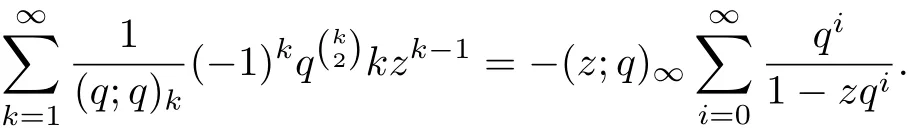
Applying the Euler expansion of
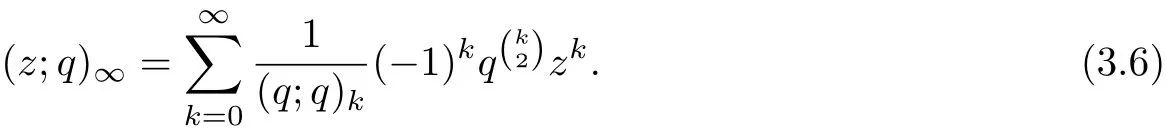
Then
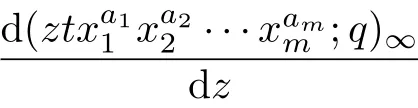
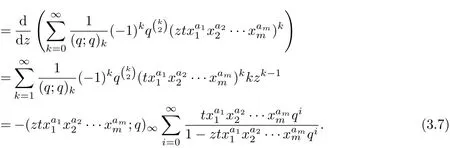
Dif f erentiating the equation(2.1)with respect to the variable z,then
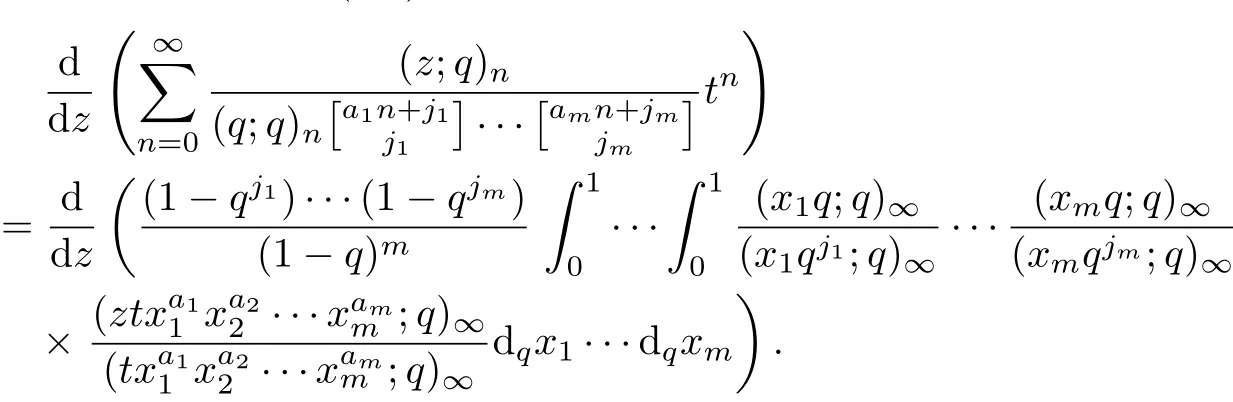
Using the identity(3.4)and(3.7),the result can be obtained.
Let m=2 in Theorem 5,then we can get the following identity.
Corollary 3Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|t|<1. Then
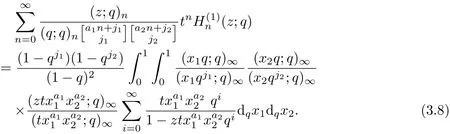
Dif f erentiating the identity of Theorem 1 with respect to the variable z twice,we can get the following identity.
Theorem 6Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1
1···xamm|<1. Then
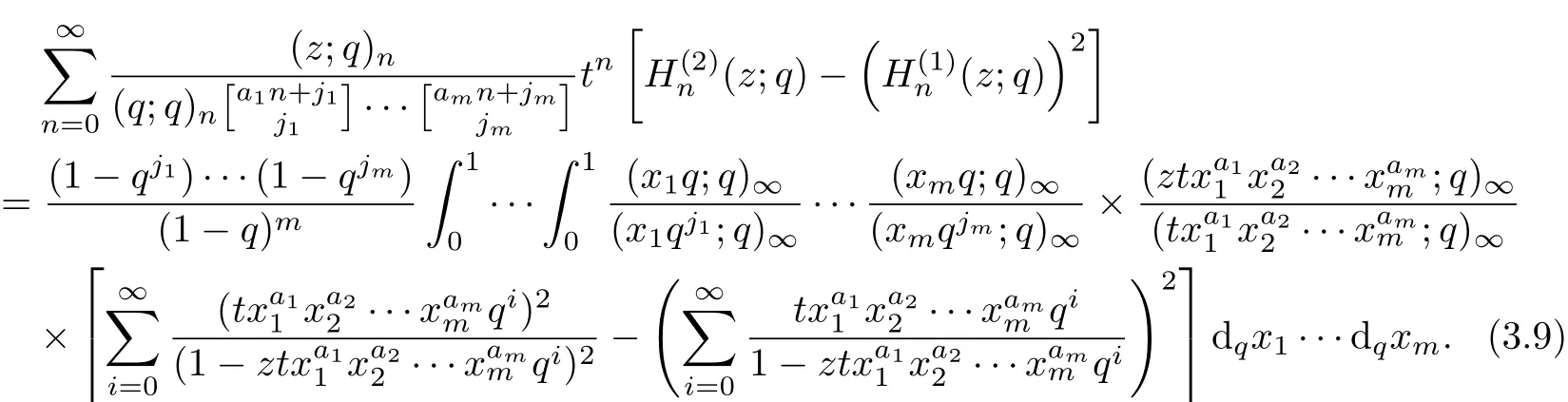
ProofDif f erentiating the equation(3.3)with respect to the variable z
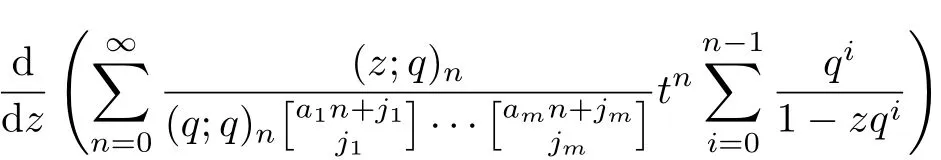
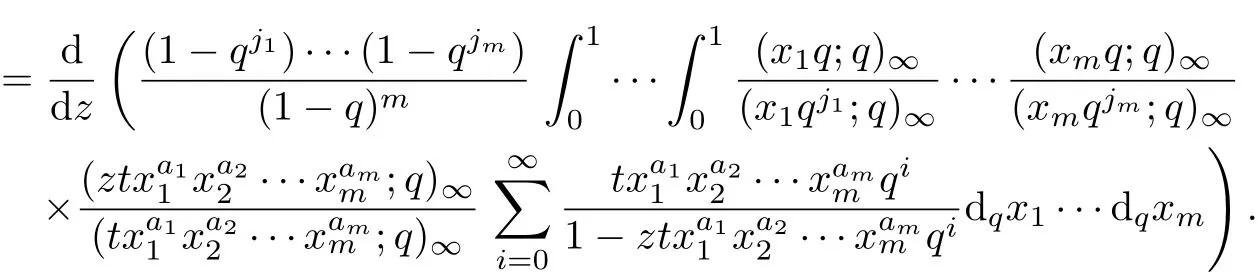
Since
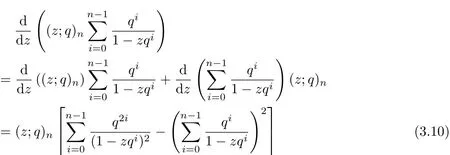
and

By equation(3.10)and(3.11),the result can be obtained.
Let m=2 in Theorem 0.6,we can get the following identity.
Corollary 4Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|tx|<1. Then
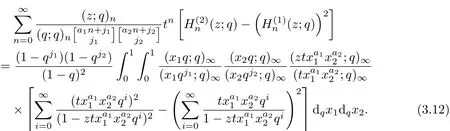
Dif f erentiating the identity of Theorem 1 with respect to the variable z for three times,the following identity can be deduced.
Theorem 7Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1
1···xam
m|<1.Then
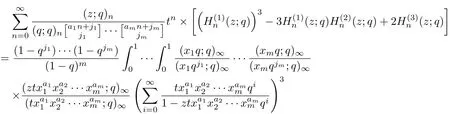
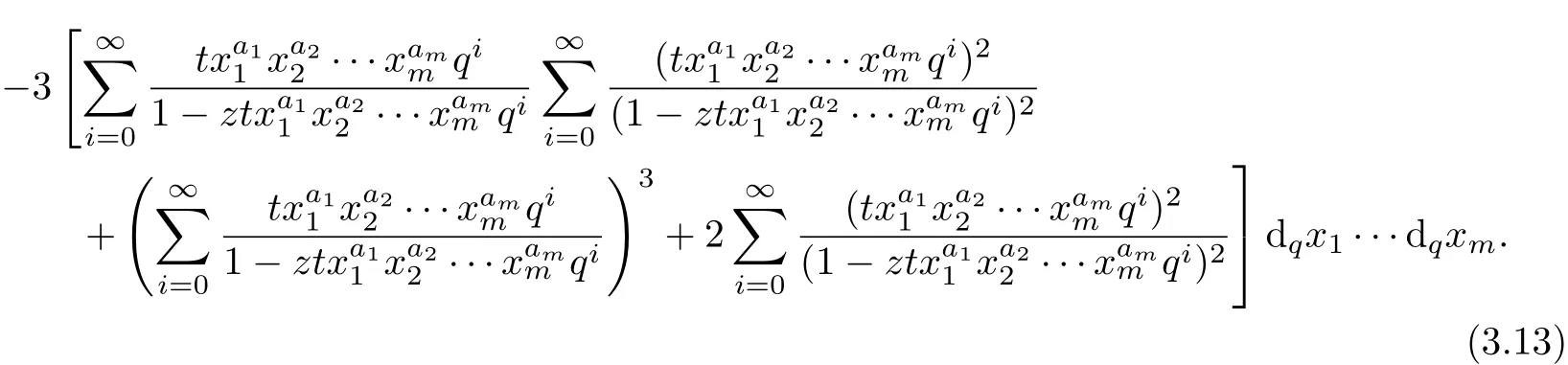
ProofDif f erentiating the equation(3.9)with respect to the the variable z
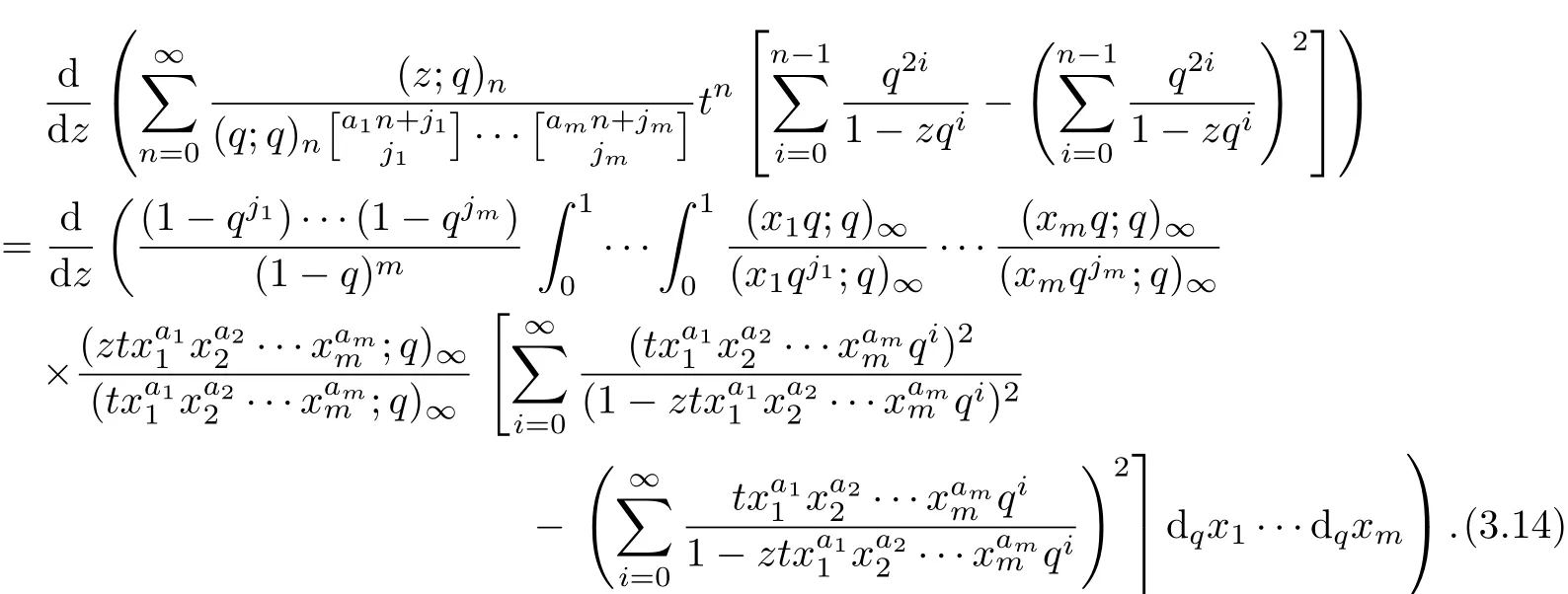
By
and

The result can be obtained.
Let m=2 in Theorem 7,we can get the following identity.
Corollary 5Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|tx|<1.
Then
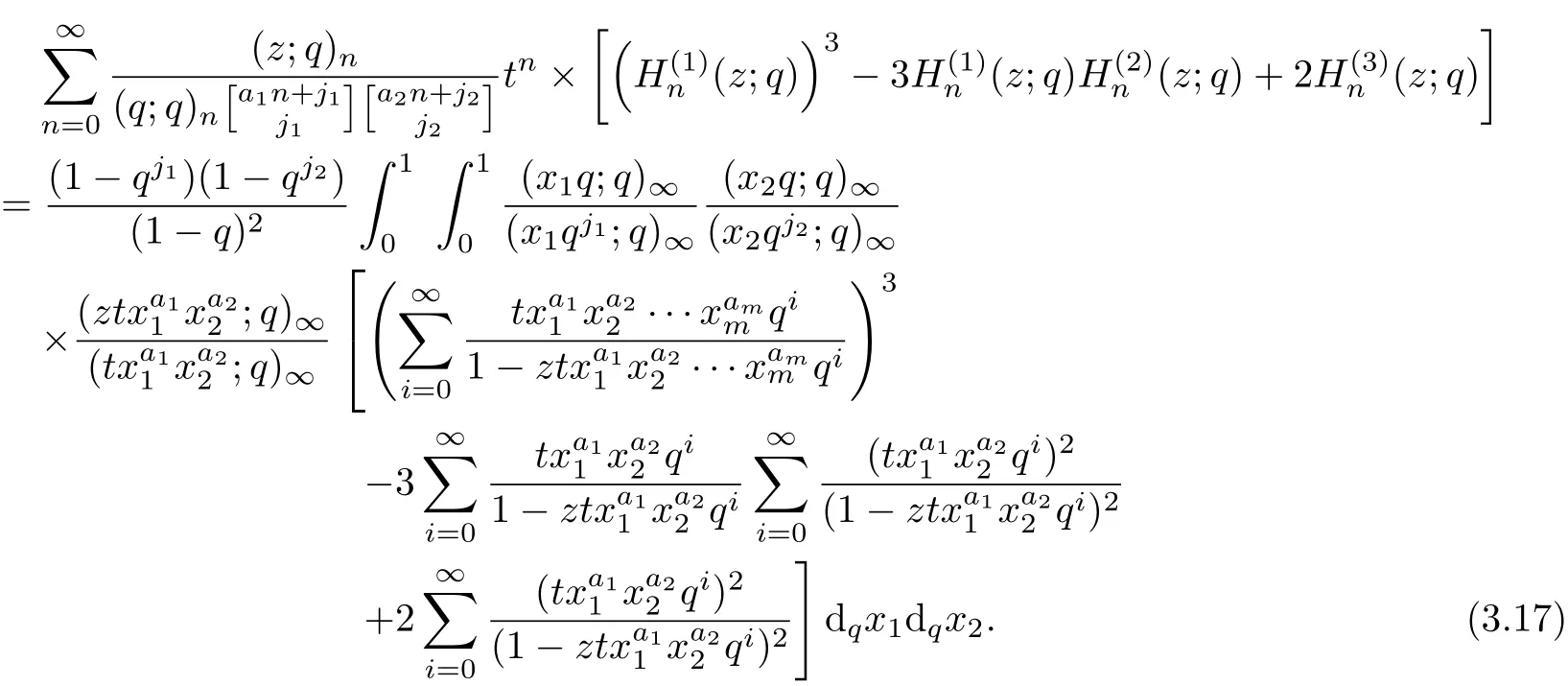
[1]GEORGE G,Mizan R.Basic Hypergeometric Series[M].Cambridge:Cambridge University Press,2004: 24-33.
[2]ANTHONY S.Sums of derivatives of binomial coefficients[J].Adv Appl Math,2009,42(1):123-134.
[3]ANTHONY S.Summation formula involving harmonic numbers[J].Analysis Math,2011,37(1):51-64.
[4]ANTHONY S.Integral forms of sums associated with harmonic numbers[J].Appl Math Comput,2009, 207(2):305-372.
tion:33D05,33C60,34A25
1002–0462(2014)04–0573–10
date:2013-03-03
Supported by the National Natural Science Foundation of China(10771093);Supported by the Youth Foundation of Luoyang Normal College(2013-QNJJ-001);Supported by the Youth Foundation of the Luoyang Institute of Science and Technology(2012QZ05)
Biographies:YANG Ji-zhen(1984-),female,native of Luoyang,Henan,a lecturer of Luoyang Normal College, M.S.D.,engages in combinatorial mathematics;WANG Yun-peng(1981-),male,native of Yingkou,Liaoning,a lecturer of Luoyang Institute of Science and Technology,M.S.D.,engages in combinatorial mathematics.
CLC number:O157.1Document code:A
 Chinese Quarterly Journal of Mathematics2014年4期
Chinese Quarterly Journal of Mathematics2014年4期
- Chinese Quarterly Journal of Mathematics的其它文章
- The Jacobi Elliptic Function Method for Solving Zakharov Equation
- Fast Parallel Method for Polynomial Evaluation at Points in Arithmetic Progression
- On the Cycle Structure of Iteration Graphs over the Unit Group
- On a Discrete Fractional Boundary Value Problem with Nonlocal Fractional Boundary Conditions
- On Laguerre Isopararmetric Hypersurfaces in ?7
- Some Notes on G-cone Metric Spaces
