Robust Adaptive Model Tracking for Distributed Parameter Control of Linear Infinite-dimensional Systems in Hilbert Space
Mark J. Balas Susan A. Frost
I.INTRODUCTION
M differen AdtiiNma l Y en esq iuo canotani oltr n os wl(hPe sDn yEs ts teh)m.e ysC u ar arreer e ntl d ye isn tchhreeirbreee nd itsl y b ay r ien npfieanwr ittieead-l interest in the control of these kinds of systems especially in flt heex i qbul e an a tuer mos cpoanc e tro s ltr fiuc etl u d[r2e,s1,2,s1m8]a.r tN ee lwe ct grei c ne p roa w l re ers u glrtisd s i,n a tnh de control theory of PDEs can be found in[11,19?20].And a very different approach to adaptive control of specifically parabolic PDEs can be seen in[21].In this paper,we want to consider how to make a linear infinite-dimensional system track the output of a finite-dimensional referencemodel in a robust fashion in the presence of persistent disturbances.
In our previous work[3?6],we have accomplished direct model reference adaptive control and disturbance rejection w ith very low order adaptive gain laws formulti-inputmultioutput(M IMO)finite-dimensionalsystems.When systemsare subjected to an unknown internaldelay,these systemsare also infinite-dimensional in nature.Direct adaptive control theory can bemodified to handle this time delay situation for infinitedimensional spaces[7].However,thisapproach doesnothandle the situation when PDEs describe the open-loop system.
This paper w ill provide a foundation for the topic of direct adaptive control on infinite-dimensional spaces.This paper considers the effect of infinite-dimensionality on the adaptive control approach of[3?6].We w ill prove here a robust stability theorem for infinite-dimensional spaces.We w ill show that the adaptively controlled system is robustly globally asymptotically stable using this new result.In order to accommodate robust behavior,we must give up the idea of all errors converging to zero and replace it w ith the idea of convergence to a prescribed neighborhood of zero whose radius is determined by the magnitude of the unmodeled disturbance.
Wewant to apply this robust theory to linear PDEsgoverned by self-adjointoperatorsw ith compact resolventsuch as linear diffusion systems.And we w ill also see some of the new technical difficultiesencountered in infinite-dimensionaldirect adaptive control and find out that the devil really is in the details.
II.ADAPTIVE ROBUST TRACK INGW ITH DISTURBANCE REJECTION
LetXbe an infinite-dimensional separable Hilbert space w p ith inner product(x,y)and corresponding norm‖x‖ ≡Also letAbe a closed linear operator with domainD(A)dense inX.Consider the linear infinite-dimensional plantw ith persistent disturbances:
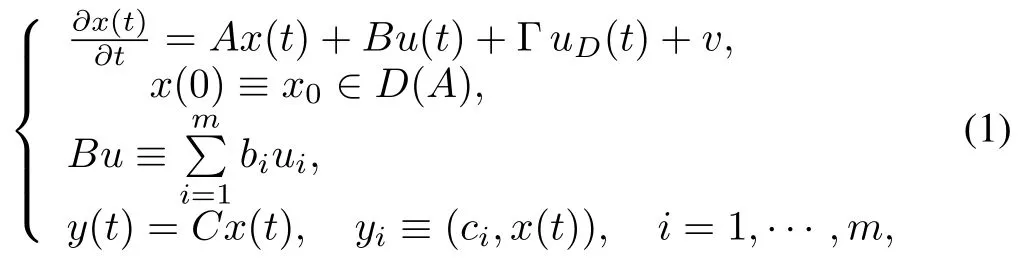
wherex∈D(A)is plant state,bi∈D(A)are actuator influence functions,ci∈D(A)are sensor influence functions,u,y∈Rmare control input and plant output,respectively,anduDis a disturbance w ith known basis functionsφD.We assumevis a bounded but unknown disturbance such that‖v‖≤M v< ∞.
In order to accomplish disturbance rejection in a direct adaptive scheme to some degree,we w ill make use of a definition,given in[17],for persistent disturbances.
Definition 1.A disturbance vectoruD∈Rqis said to be persistent if it satisfies the disturbance generator equations:‰
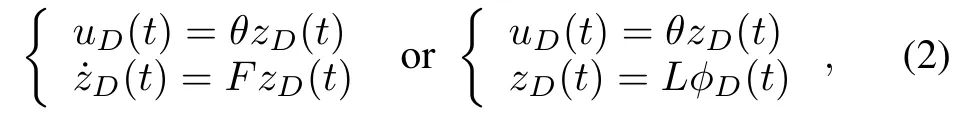
whereFis amarginally stablematrix andφD(t)is a vector of known functions form ing a basis for all such possible disturbances.This is known as“a disturbance w ith known waveform but unknown amplitudes”.
Theobjective of control in thispaper is to causeoutputy(t)of the plant to robustly asymptotically track outputym(t)of a linear finite-dimensional referencemodel given by
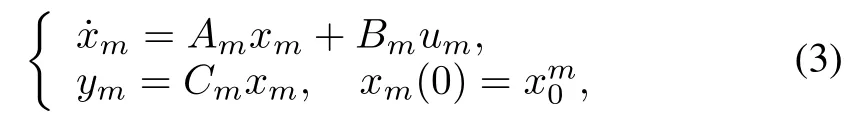
where reference model statexm(t)is anNm-dimensional vector w ith reference model outputym(t)having the same dimension as plant outputy(t).In general,the plant and reference models need not have the same dimension.The excitation of the referencemodel is accomplished via vectorum(t)which is generated by
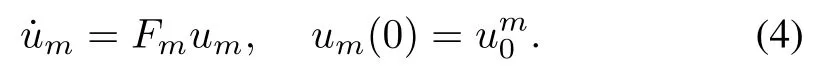
The reference model parameters(Am,Bm,Cm,Fm)w ill be assumed completely known.Themeaning of robustasymptotic tracking is as follows.
We define the output error vector as
whereN(0)is a predeterm ined neighborhood of zero vector.
The control objective w ill be accomplished by a direct adaptive control law in the form of
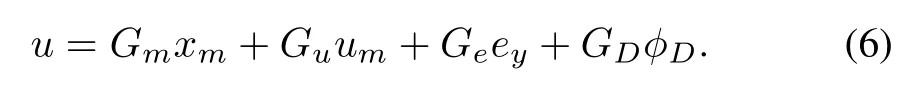
The direct adaptive controller w ill have adaptive gains given by
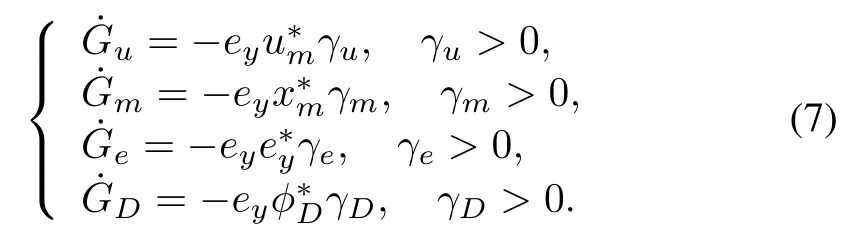
III.IDEAL TRAJECTORIES
We define the ideal trajectories for(1)as
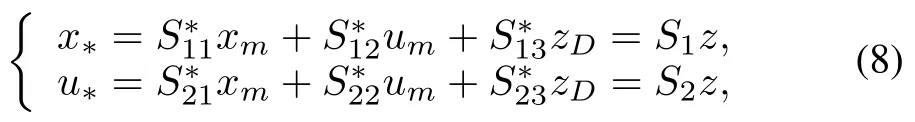
w ithz≡[xm um zd]T∈RL,where the ideal trajectoryx?(t)is generated by the ideal controlu?(t)from
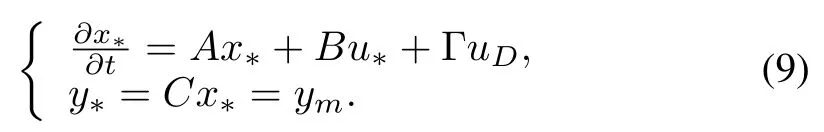
If such ideal trajectoriesexist,theyw illbe linear combinations of the referencemodel state,disturbance state,and reference model input(8),and they w ill produce exact output tracking in a disturbance-free plant(9).
By substitution of(8)into(9)using(3)and(4),we obtain the linearmodelmatching conditions,i.e.,
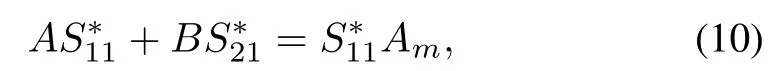
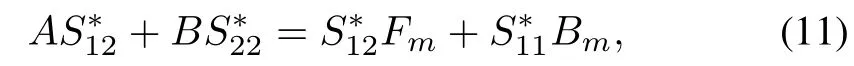


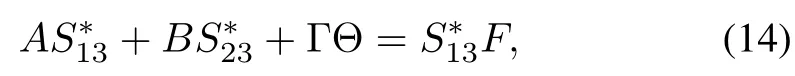

The model matching conditions(10)–(15)are necessary and sufficient conditions for the existence of the ideal trajectories in the form of(8).Modelmatching conditions(10)–(15)can be rew ritten as
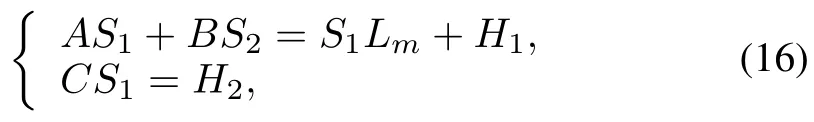
IV.IDEAL TRAJECTORY EX ISTENCE AND UNIQUENESS:NORMAL FORM
To determine the conditions for existence and uniqueness of the ideal trajectories,we need two lemmas.
Lemma 1.IfCBis nonsingular,thenP1≡B(CB)?1Cis a(non-orthogonal)bounded projection onto the range ofB,R(B),along the null space ofC,N(C)w ith the complementary bounded projectionP2≡I?P1,andX=R(B)⊕N(C)as well asD(A)=R(B)⊕[N(C)∩D(A)].
Proof.Consider
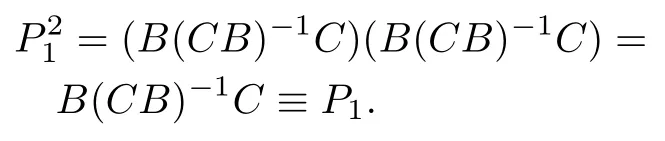
HenceP1is a projection.
Clearly,R(P1)?R(B)andz=Bu∈R(B)which implies
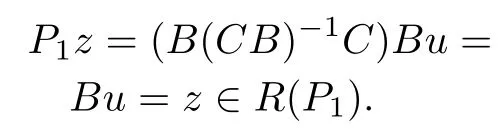
Therefore,R(P1)=R(B).
AlsoN(P1)=N(C)becauseN(C)?N(P1)andz∈N(P1)implies thatP1z=0,indicating thatCP1z=CB(CB)?1Cz=0 orN(P1)?N(C).SoP2is a projection ontoR(B)alongN(C).ButP?2/=P2,so it is notan orthogonal projection in general.We haveX=R(P1)⊕N(P1);henceX=R(B)⊕N(C).
Sincebi∈D(A),we haveR(B)?D(A).Consequently,D(A)=(R(B)∩D(A))⊕(N(C)∩D(A))=R(B)⊕(N(C)∩D(A)).The projectionP1is bounded since its range is finite-dimensional,and the projectionP2is bounded because‖P2‖ ≤1+‖P1‖ < ∞.
This completes the proof of Lemma 1.
Now for the above pair of projections(P1,P2),we have
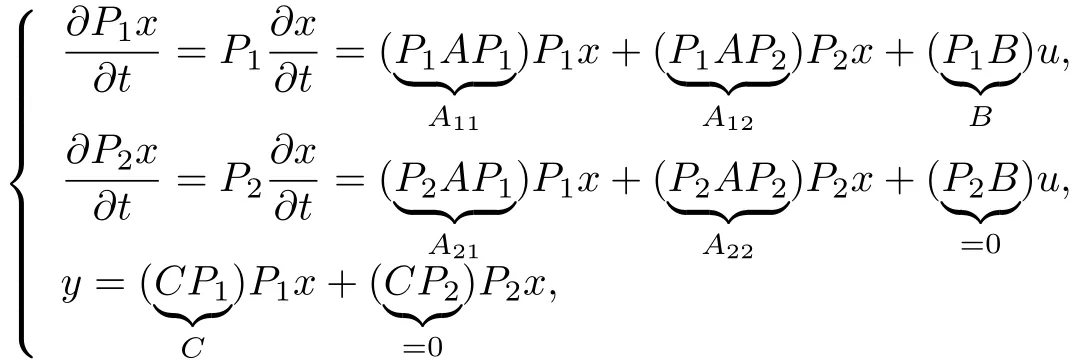
which implies that
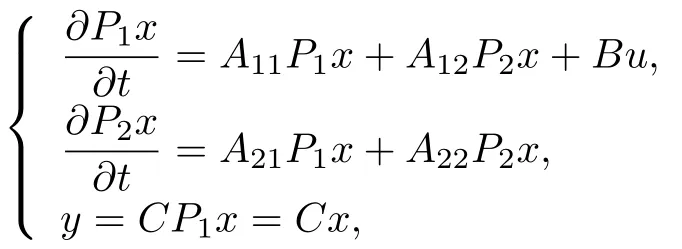
because
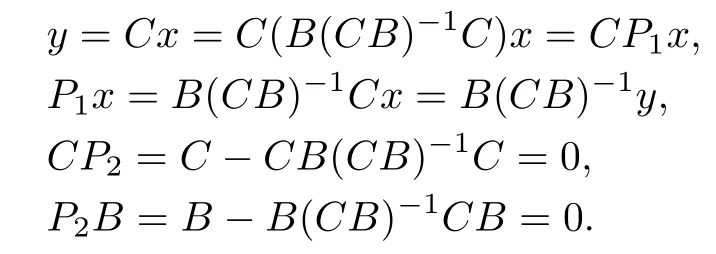
Lemma 2.IfCBis nonsingular,then there exists an invertible,bounded linear operatorW≡:X→≡R(B)×l2such that≡W B=and
This coordinate transformation can be used to put(1)into the normal form,i.e.,
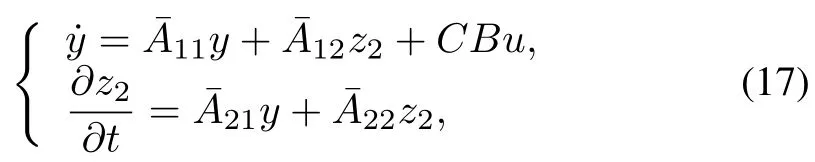
Proof.SinceXis separable,we can letN(C)=be an orthonormal basis.
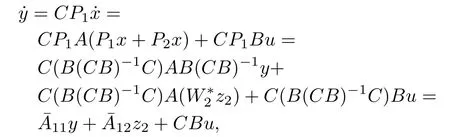
and
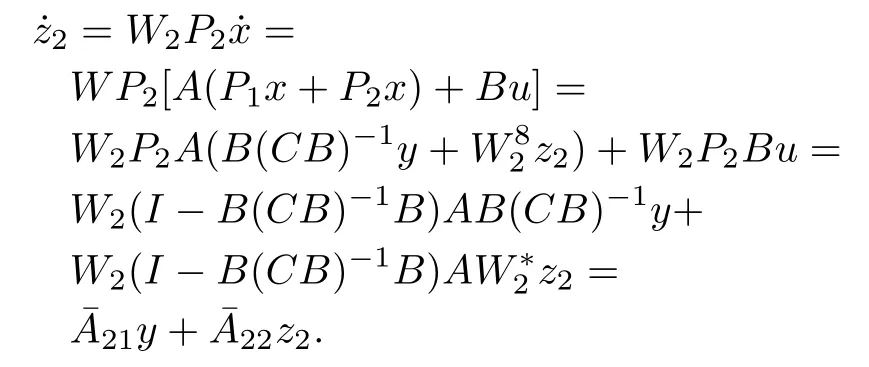
This yields the normal form(17).
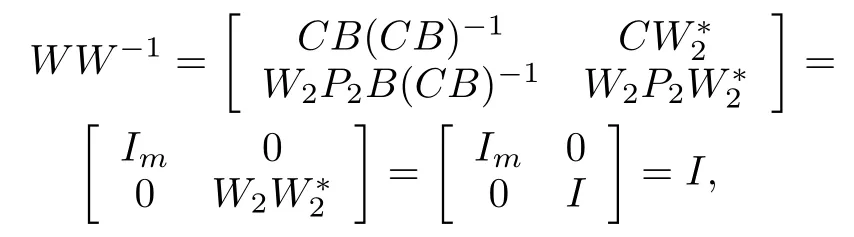
becauseR(W?2)?N(C).
Furthermore,W?1W=P1+W?2W2P2=P1+P2=I,becauseW2W?2=IonN(C).Also direct calculation yields
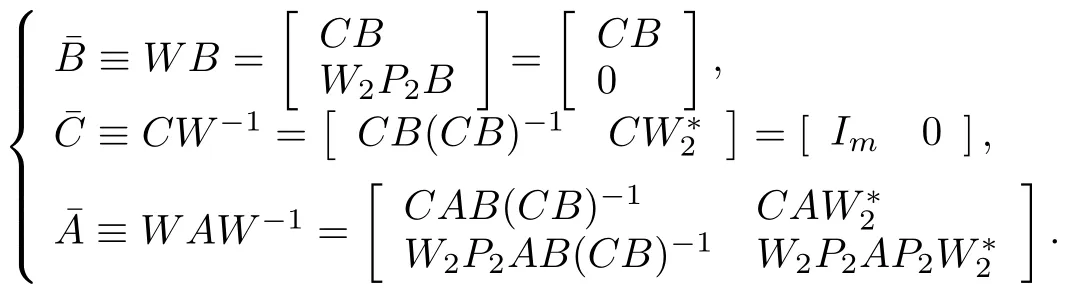
This completes the proof of Lemma 2.
Now we can prove the follow ing theorem about the existence and uniqueness of ideal trajectories.
Theorem 1.AssumeCBis nonsingular.Thenσ(Lm)=σ(Am)∪ σ(Fm)∪ σ(F)? ρ(22)whereρ(22)≡{λ ∈Csuch that(λI?22)?1:l2→l2is a bounded linear operator}if and only if there exist unique bounded linear operator solutions(S1,S2)satisfying matching conditions(16).
Note that we can also w riteσ(Lm)∩ σ(22)=where
Proof.Defineand≡WH1=.From(16),we obtain
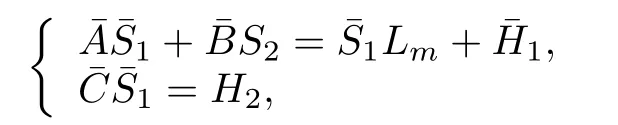
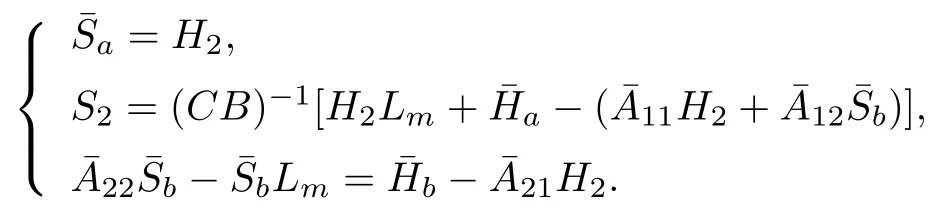
We can rew rite the last equation as
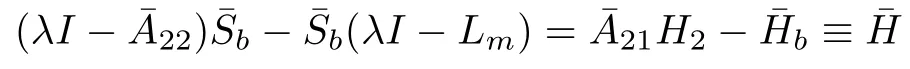
for all complexλ.Now assume thatLmis simple and therefore provides a basis of eigenvectorsfor RL.This is not essential but w ill make this part of the proofeasier to understand.The proof can be done w ith generalized eigenvectors and the Jordan form.So we have
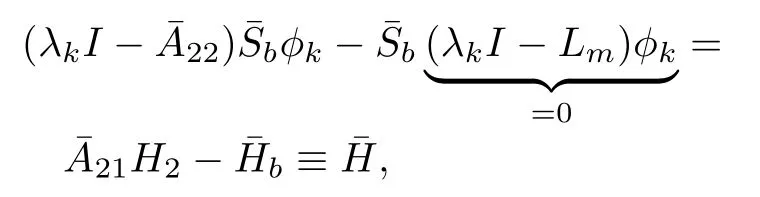
which implies that
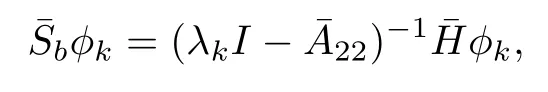
becauseλk∈ σ(Lm)? ρ(22).Thuswe have
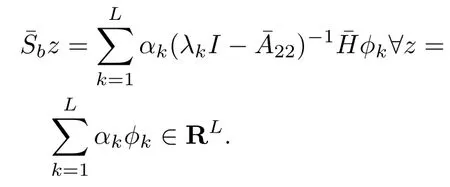
Sinceλk∈ σ(Lm)? ρ(22),all(λk I?22)?1are bounded operators.
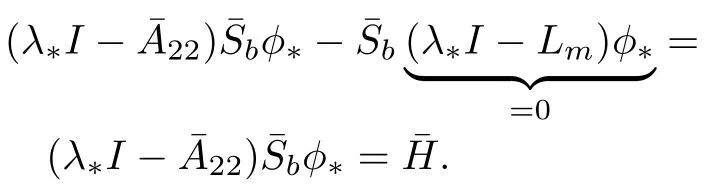
In this case,three things can happen when,λ?∈ σ(22):
1)(λ?I?22)can fail to be one-to-one so multiple solutions ofˉSbw ill exist;
2)R(λ?I?22)can fail to be all ofX,so no solutionˉSbmay occur;
3)(λ?I?22)?1can fail to be a bounded operator so solutionˉSbmay be unbounded.
In all cases these three alternatives lead to lack of unique bounded operator solutions forS1.
The proof of Theorem 1 is complete.□
It is possible to relate the point spectrumσp(22)≡'λsuch thatλI?22is not one-to-one“to the setZof transmission(orblocking)zerosof(A,B,C).As in the finitedimensional case[13],we can see that
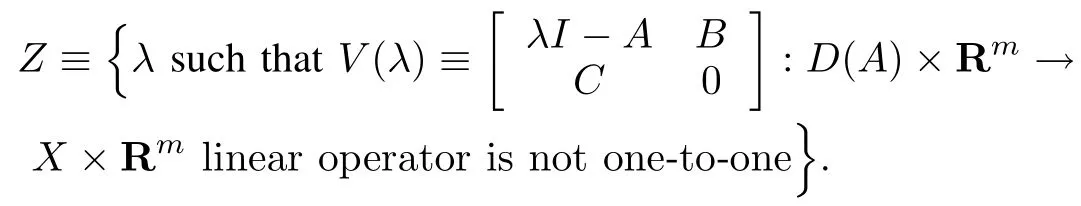
Lemma 3.Z=σp(22)≡{λsuch thatλI?22is not one-to-one}is called the point spectrum of22.
So the transm ission zeros of the infinite-dimensional openloop plant(A,B,C)are the eigenvalues of its zero dynam ics(22,12,21).
Proof.From
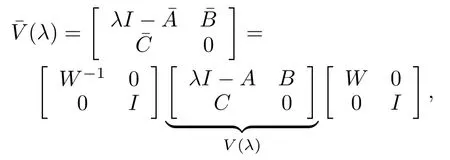
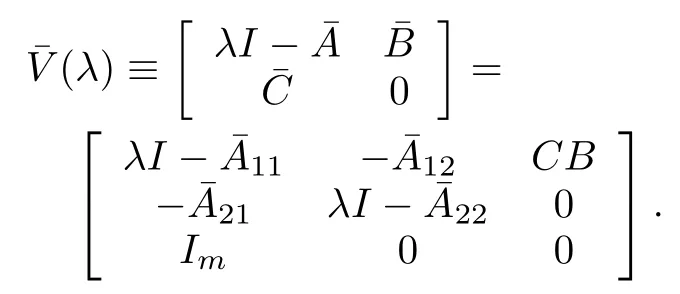
This completes the proof of Lemma 3.
Using Lemma 3 and Theorem 1,we have the follow ing internalmodel principle.
Corollary 1.AssumeCBis nonsingular andσ(22)=σp(A22)=σp(P2AP2),whereThere existunique bounded linear operator solutions(S1,S2)satisfying thematching conditions(16)if and only ifσ(Lm)∩Z=,i.e.,no eigenvalues of(Am,Fm,F)can be zeros of(A,B,C).Note that
λI?22is not one-to-one?
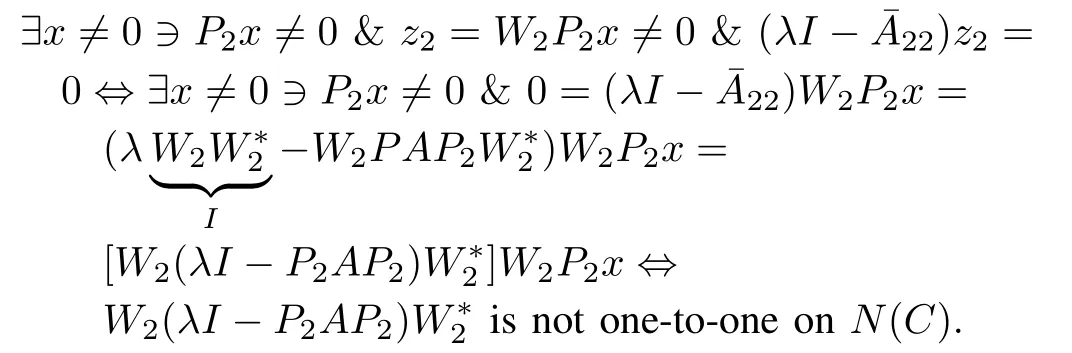
ButW2is an isometry onN(C),soσp(22)=σp(P2AP2).
V.STABILITY OF THE ERROR SYSTEM:ALMOST STRICT DISSIPATIVITY
The error system can be found from(1)and(9)by fi rst defininge≡x?x?andΔu≡u(píng)?u?.Then we have
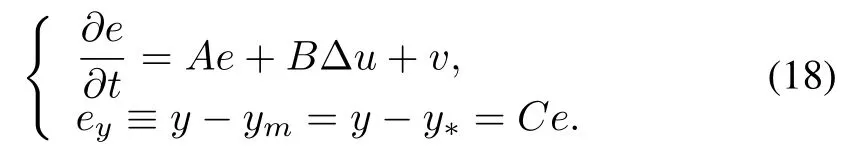
Now consider the definition of strict dissipativity for infinitedimensional systems and the general form of this adaptive error system to prove stability.The main theorem of this section w ill be utilized later to assess the convergence and stability of the adaptive controller w ith disturbance rejection for linear diffusion systems.
Noting that there can be some ambiguity in the literature w ith the definition of strictly dissipative systems,wemodify the suggestion of Wen in[8]for finite-dimensional systems and expand it to include infinite-dimensional systems.
Definition 2.The triple(Ac,B,C)is said to be strictly dissipative(SD)ifAcis a densely defined,closed operator onD(Ac)?Xwhich is a complex Hilbert space w ith inner product(x,y)and corresponding norm‖x‖≡and generates aC0sem igroup of bounded operatorsU(t),and(B,C)are bounded input/output operatorsw ith finite rankMwhereB:Rm→XandC:X→Rm.In addition,there exist symmetric positive bounded operatorsPand Q onXsuch that 0≤pmin‖e‖2≤(Pe,e)≤pmax‖e‖2,0≤qmin‖e‖2≤(Qe,e)≤qmax‖e‖2,i.e.,PandQare bounded and coercive,and

whereC?is the adjoint of the operatorC.
We also say that(A,B,C)is almost strictly dissipative(ASD)when there exists aG?∈Rm×msuch that(Ac,B,C)is SD w ithAc≡A+BG?C.Note that ifP=Iin(19),by the Lumer-Phillips theorem(see[10],p405),we would have
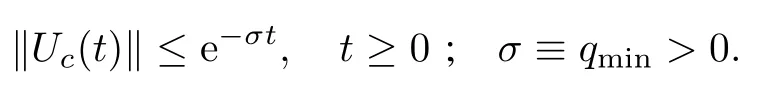
Henceforth,we w illmake the follow ing set of assumptions.
Hypothesis 1.Assume the follow ing:
2)Ais a densely defined,closed operator onD(A)?Xand generates aC0semigroup of bounded operatorsU(t);
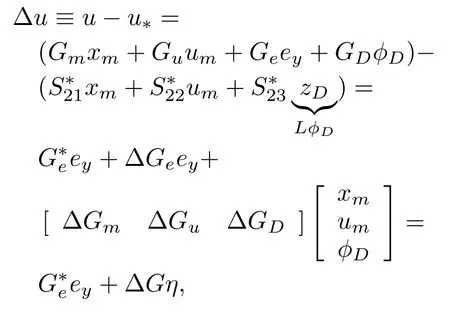
whereΔG≡G?G?,G≡[Ge Gm Gu GD],G?≡From(1),(6),(7),(18),and(19),the error system becomes
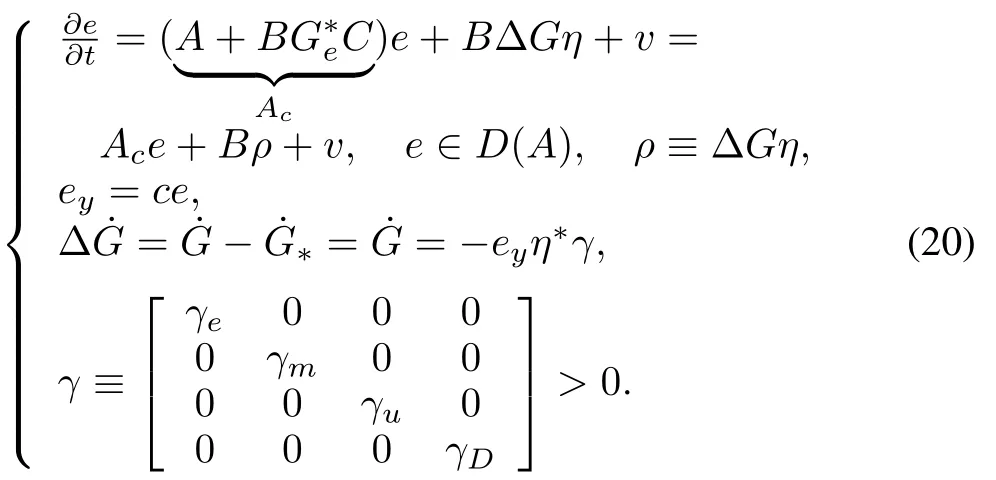
SinceB,Care finite rank operators,so isTherefore,w ithD(Ac)=D(A)generates aC0sem igroupUc(t)becauseAdoes(see[17],Theorem 2.1,p497).Furthermore,by Theorem 8.10(p157)in[1],x(t)remains inD(A)and is differentiable there for allt≥0.This isbecauseF(t)≡Bρ=BΔGηis continuously differentiable inD(A).
We see that(20)is the feedback interconnection of an infinite-dimensional linear subsystem w ithe∈D(A)?Xand a finite-dimensional subsystem w ithΔG∈Rm×m.This can be w ritten in the follow ing form using
D≡D(A)×Rm×m?≡X×Rm×m:
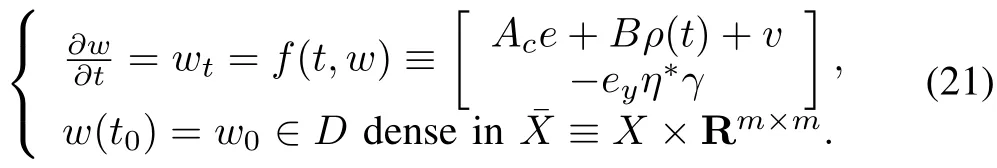
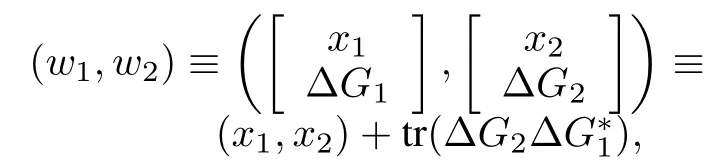
which w illmake it a Hilbert space aswell.
The follow ing robust stabilization theorem shows that convergence to a neighborhood w ith radius determ ined by the supremum norm ofvis possible for a specific type of a p daptive error system.In the follow ing,we denote‖M‖2≡as the tracenorm of amatrixMwhereγ>0.
Theorem 2(Robust stabilization).Consider the coupled system of differential equations
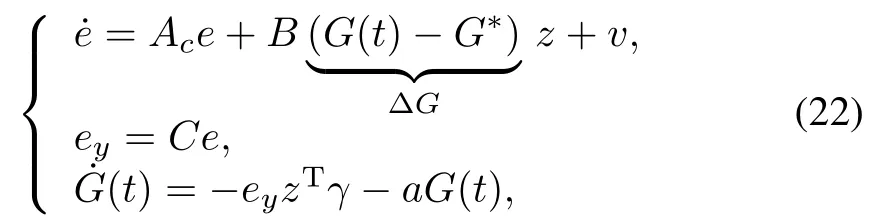
wheree,v∈D(Ac),z∈Rmand≡X×Rm×mis a Hilbert space w ith inner product≡(e1,e2)+trG1γ?1G2,norm≡,G(t)is them×madaptive gain matrix,andγis any positive definite constant matrix of appropriate dimension.Assume the follow ing:
1)(A,B,C)is ASD w ithAc≡A+BG?C;
2)There existsMG>0 such that
3)There existsMυ >0 such that supt≥0‖v(t)‖ ≤M v<∞;
4)There existsα>0 such thatwhereqm in,pm ax are defined in Definition 2;
5)The positive definite matrixγsatisfies tr(γ?1)≤
Then the gain matrixG(t),is bounded,and statee(t)exponentially w ith rate e?a tapproaches the ball of radius,
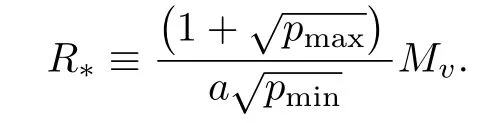
The proof of Theorem 2 is in Appendix.
Now we can prove the robust stability and convergence of the directadaptive controller(4)in closed-loop w ith the linear infinite-dimensional plant(1)and(2).
Theorem 3.Under Hypothesis 1,we have robust state and output tracking of the reference model,i.e.,N(0,R?)and sinceCis a bounded linear operator,we havew ith bounded adaptive gains
Proof. Follows directly from the application of Theorem 2 to the error system (18) or (22).
Note that uniform continuity is not needed since Barbalat′s lemma[15]is not invoked here.
VI.APPLICATION:ADAPTIVE CONTROL OF UNSTABLE DIFFUSION EQUATIONS DESCRIBED BY SELF-ADJOINT OPERATORSW ITH COMPACT RESOLVENT
We w ill apply the above direct adaptive controller on the follow ing single-input/single-output Cauchy problem:
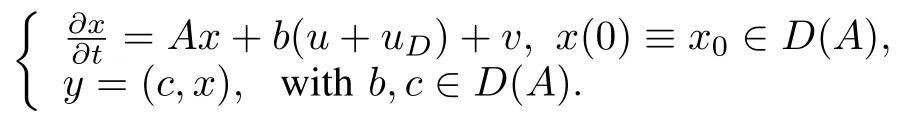
And the referencemodelw ill be
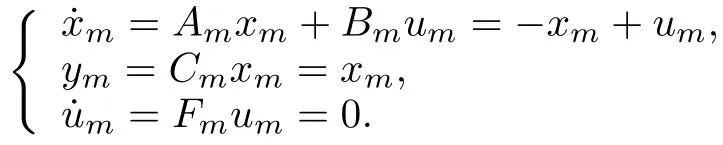
For this application,wew ill assume the disturbances are step functions.Note that the disturbance functions can be any basis function as long asis bounded,in particular sinusoidal disturbances are often applicable.So we have≡ 1 andwhich implies F=0 andθD=1.
Let u=Gey+GDw ith
Wew illassume that A is closed and densely defined,but is also a self-adjointoperatorw ith compact resolvent.Thismeans A has discrete real spectrum:λ1≥ λ2≥ ···→ ?∞ andis an orthonormal sequence of eigenfunctions(see[9],Theorem 6.29,p187).Assume λk/=0, ?k=1,2,···.Only a finite number of the eigenvaluesmaybe unstable(or positive);so we w ill say thatλ1≥ λ2≥ ···≥ λN≥ ?σ ≥λN+1→?∞,whereσ>0 is the desired stability margin.
Define the orthogonal projection operators as x=PNx+PRx w ith
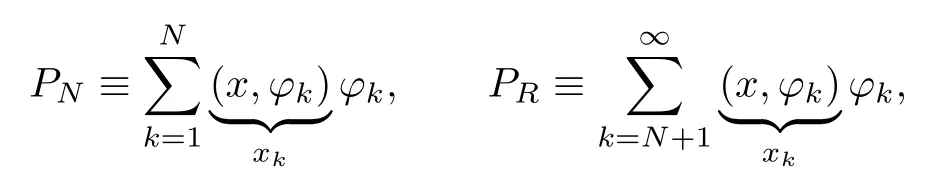
Let the sensor and actuator influence functions be the same and entirely in SN,that is,c≡b=w ith all bk/=0 and choose G?≡ ?g?< 0.Then Ac=A ? g?b?b remains self-adjointw ith discrete spectrum,and we have
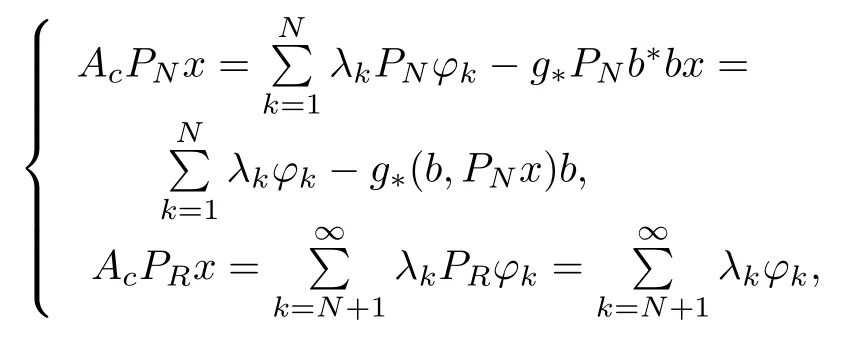
because PNb=b=c.So Re(PAcx,x)=Re(PAcPNx,x)+Re(PAcPRx,x),and in Definition 2,wew ill use P=I,and obtain the follow ing results from[17]:[b1,···,bN]T,is a finitedimensional system that is controllable/observable if and only if bk/=0.
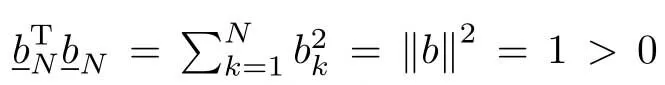
3)We have and all zeros of the open-loop are stable when
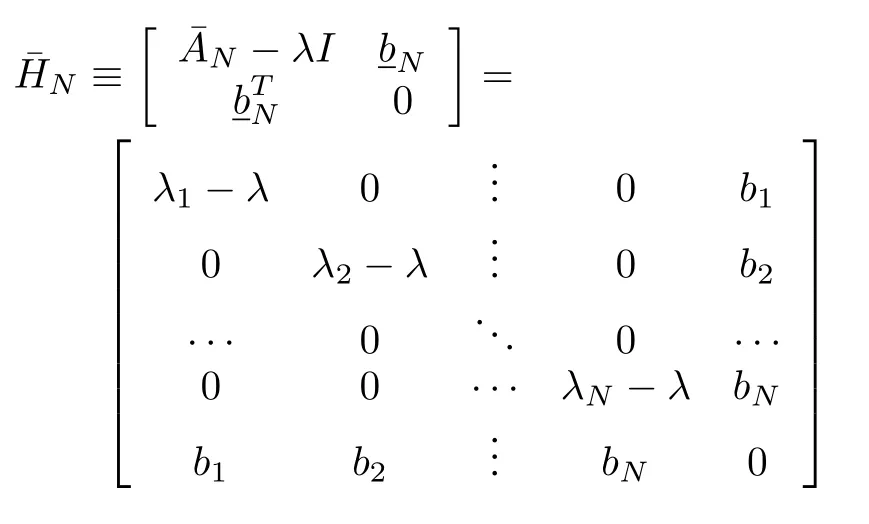
is nonsingular for all Re(λ) ≥ 0(see[14],p286).Soisalmoststrictly positive real(ASPR)ifand only if
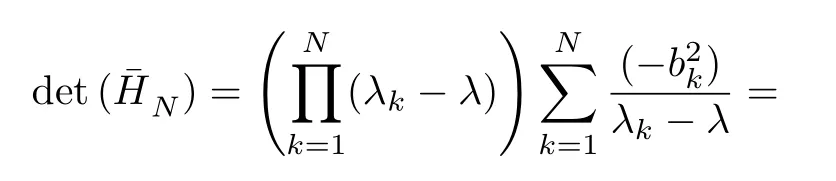
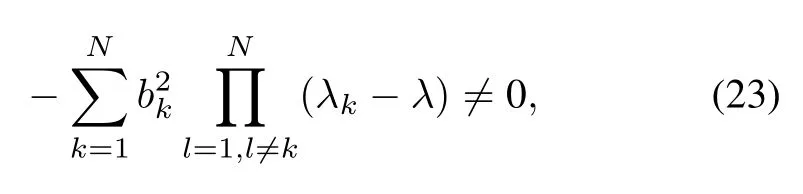
for all Re(λ)≥ 0 and Re(λ)/= λk,because in thisapplication all eigenvalues are distinct and nonzero.
4)There exists G?≡ ?g?such that(Ac≡ A?g?cc?,B ≡b,C ≡ c?)is SD and

As long as(23)is satisfied,we can apply Theorem 3,and we have robust state tracking,and robust reference model tracking,w ith bounded adaptive gains G≡[GmGuGeGD]in the presence of persistent disturbances,via the direct adaptive controller.
Example.Anunstableheatequation
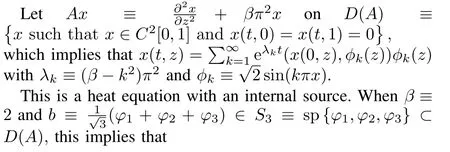
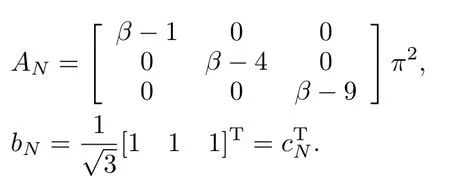
This system satisfies(6)and(7),and has poles at, ?, ?and zeros at ?49.35, ? 3.29,so is the minimum phase w ith cNbN=1>0 and therefore ASPR.Consequently,the directadaptive controller in(4)w illproduce output trackingw ith bounded adaptive gains in the presence of step disturbances.
VII.PERTURBATION RESULTS
Theprevious resultsdepend uponb=PN b∈SN.However,it is possible to allowb≡PN b+εPR b∈D(A),ε≥0.DefinexN≡PN xandxR≡PR x,which implies that
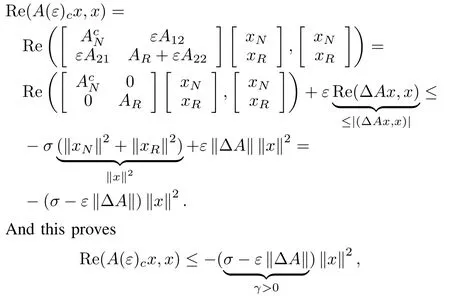
for all 0≤ε<And we have that(A(ε)c,B,C)is SD and we can apply Theorem 2 again.Therefore,for smallε>0,all previous results are still true and we do not needbbeing entirely confined inSN.
VIII.CONCLUSIONS
In Theorem 2,we prove a robust stabilization result for linear dynamic systemson infinite-dimensional Hilbertspaces under the hypothesis of almost strict dissipativity for infinitedimensional systems.This idea is an extension of the concept ofm-accretivity for infinite-dimensional systems(see[9],p278?280).In Theorem 3,we show that adaptive model tracking is possible w ith a very simple direct adaptive controller that knows very little specific information about the system it is controlling.This controller can also mitigate persistent disturbances.There is no use of Barbalat′s lemma which requires certain signals to be uniform ly continuous.However,we do not get something for nothing;we must relax the idea that all signals w ill converge to 0 and replace it w ith the idea that they w ill be attracted exponentially to a prescribed neighborhood whose size depends on the norm of the completely unknown disturbance.In order to make such an infinite-dimensional system track a finite-dimensional reference model,we use the idea of ideal trajectories,and in Theorem 1 we show the conditions for existence and uniqueness of these ideal trajectories w ithout requiring any deep know ledge of the infinite-dimensional plant.
We apply these results to a general infinite-dimensional linear systems described by self-adjoint operators w ith compact resolvent,in particular unstable diffusion problems using a single actuator,sensor and direct adaptive output feedback.Such systemsareshown to beable to robustly track theoutputs of a finite-dimensional reference model in the presence of persistent disturbances.
These results do not require deep know ledge of specific properties or parameters of the system to accomplish model tracking.And they do not require that the disturbances enter through the same channelsas the control.Finally,it ispossible to substantially expand the results in Theorem 2 to nonlinear infinite-dimensional systems,butwe have elected here to take a small(baby)step forward and show the possibilities of adaptive control for infinite-dimensional systems.
APPENDIX
Proof of Theorem 2.From(21)and Pazy corollary(see[1],Corollary 2.5,p107),we have a well-posed system in(23)whereAcis a closed operator,densely defined onD(AC)?Xand generates aC0sem igroup onX,and all trajectories starting inD(AC)w ill remain there.Hence we can differentiate signals inD(AC).
Consider the positive definite function
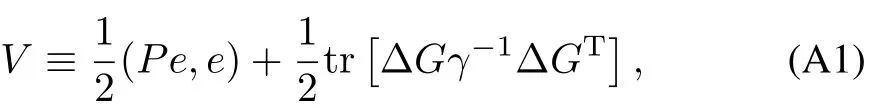
whereΔG(t)≡G(t)?G?andPsatisfies(19).
Taking the time derivative of(A1)(this can be done?e∈D(AC))and substituting(22)into the result yields
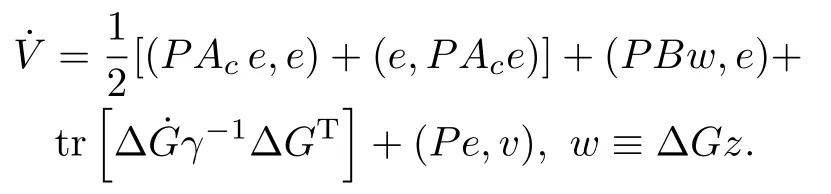
Invoking the equalities in Definition 2 of strict dissipativity,usingxTy=tr[yxT],and substituting(23)into the last expression,we get
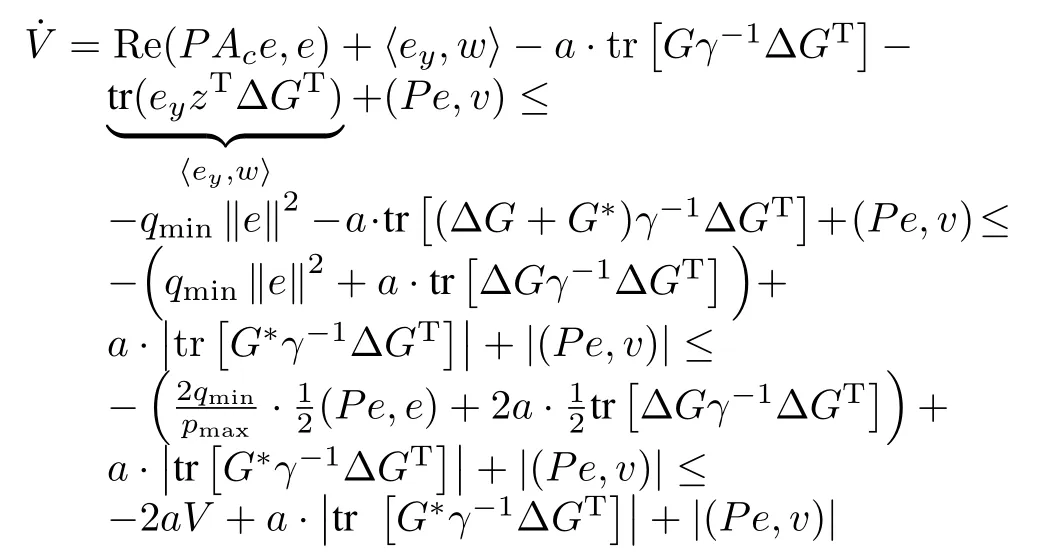
w ith〈ey,w〉≡Now,using the Cauchy-Schwartz inequality
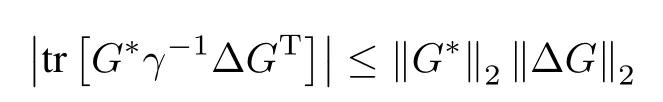
and
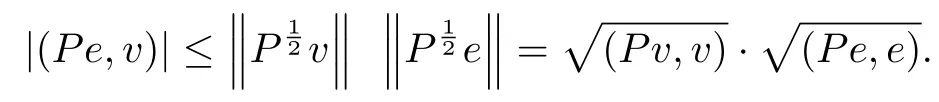
We have

Therefore,
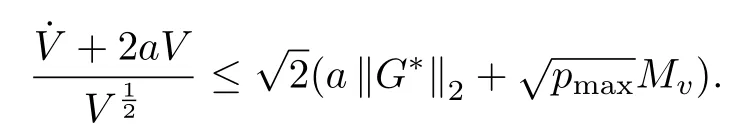
Now,using the identity tr[ABC]=tr[CAB],we have
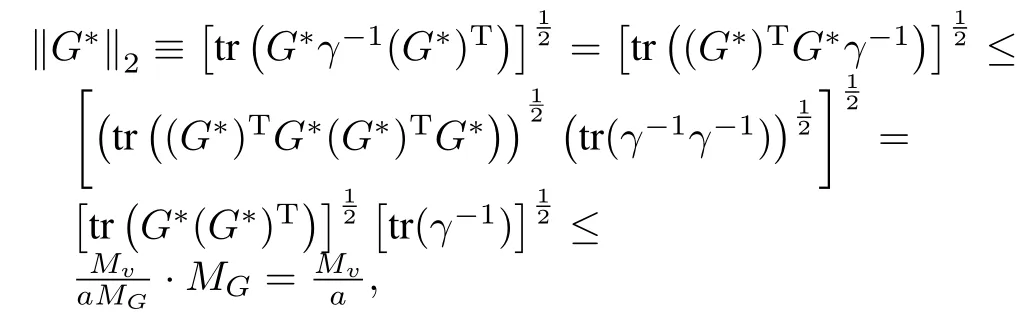
which implies that
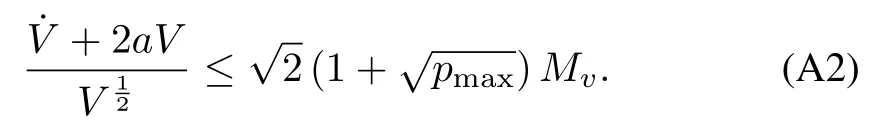
From
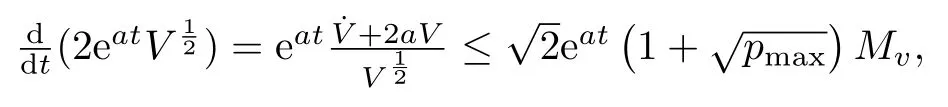
Integrating this expression we have

Therefore,
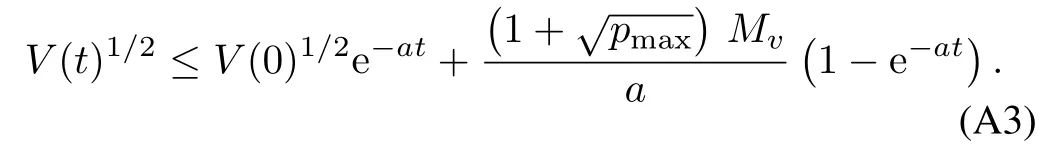
The functionV(t)is a norm function of statee(t)and matrixG(t).So,sinceV(t)1/2is bounded for allt,thene(t)andG(t)are bounded.We also obtain the follow ing inequality:
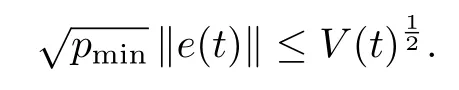
Substitution of this into(A3)gives us an exponential bound on statee(t),i.e.,
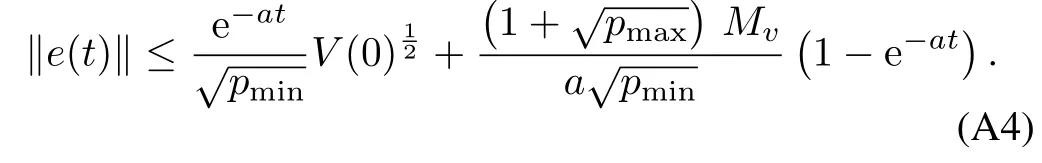
Taking the limit superior of(A4),we have
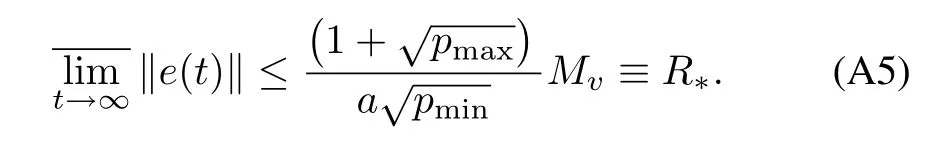
And the proof is complete.□
[1]Pazy A.Semigroups of Linear Operators and Applications to Partial Differential Equations.New York:Springer,1983.
[2]D’A lessandro D.Introduction to Quantum Controland Dynam ics.London:Chapman&Hall,2008.
[3]Balas M,Erw in R S,Fuentes R.Adaptive control of persistent disturbances for aerospace structures.In:Proceedingsof the AIAA Guidance,Navigation and Control Conference.Denver,2000.
[4]Fuentes R J,Balas M J.Direct adaptive rejection of persistent disturbances.Journal of Mathematical Analysis and Applications,2000,251(1):28?39
[5]Fuentes R,Balas M.Disturbance accommodation for a class of tracking controlsystems.In:Proceedingsof the AIAA Guidance,Navigation and Control Conference.Denver,Colorado,2000.
[6]Fuentes R J,Balas M J.Robust model reference adaptive control w ith disturbance rejection.In:Proceedings of the American Control Conference.Anchorage,AK:IEEE,2002.4003?4008
[7]Balas M,Gajendar S,Robertson L.Adaptive tracking control of linear systemsw ith unknown delays and persistent disturbances(orWho You Callin’Retarded?).In:Proceedings of the AIAA Guidance,Navigation and Control Conference.Chicago,IL,2009.
[8]Wen JT.Time domain and frequency domain conditions for strict positive realness.IEEE Transactions on Automatic Control,1988,33(10):988?992
[9]Kato T.Perturbation Theory for LinearOperators.New York:Springer,1980.
[10]Renardy M,Rogers R.An Introduction to PartialDifferentialEquations.New York:Springer,1993.
[11]Curtain R,Pritchard A.Functional Analysis in M odern Applied Mathematics.Academ ic:Academ ic Press,1977.
[12]BalasM J.Trends in large space structure control theory:fondesthopes,w ildest Dreams.IEEE Transactions on Automatic Control,1982,27(3):522?535
[13]Balas M,Fuentes R.A non-orthogonal projection approach to characterization of almostpositive realsystemsw ith an application to adaptive control.In:Proceedings of the American Control Conference.Boston,MA,USA:IEEE,2004.1911?1916
[14]Antsaklis P,M ichel A.A Linear Systems Primer.Boston:Birkhauser,2007.
[15]Popov V M.Hyperstability ofControlSystems.Berlin:Springer,1973.
[16]Kailath T.LinearSystems.New York:Prentice-Hall,1998.448?449
[17]Balas M,Frost S.Distributed parameter direct adaptive control using a new version of the Barbalat-Lyapunov stability result in Hilbert space.In:Proceedingsof AIAA Guidance,Navigation and ControlConference.Boston,MA:AIAA,2013.
[18]Kothari D,Nagrath I.M odern Power System Analysis.New York:M cGraw-Hill,2003.
[19]Cannarsa P,Coron JM,A labau-Boussouira F,Brockett R,Glass O,Le Rousseau J,Zuazua E.Control of Partial Differential Equations:Cetraro,Italy 2010,Editors:Piermarco Cannarsa,Jean-M ichel Coron(Lecture Notes in Mathematics/C.I.M.E.Foundation Subseries).Berlin Heidelberg:Springer,2012.
[20]Troltzsch F.Optimal Control of Partial Differential Equations.Providence,RI:American Mathematical Society,2010.
[21]Smyshlyaev A,Kristic M.Adaptive ControlofParabolic PDEs.Princeton:Princeton University Press,2010.
 IEEE/CAA Journal of Automatica Sinica2014年3期
IEEE/CAA Journal of Automatica Sinica2014年3期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Continuous Action Reinforcement Learning for Control-Affine Systems with Unknown Dynam ics
- An Improved Result of Multiple Model Iterative Learning Control
- Adaptive Iterative Learning Control for a Class of Nonlinear Time-varying Systems with Unknown Delays and Input Dead-zone
- Event-Triggered Optimal Adaptive Control Algorithm for Continuous-Time Nonlinear Systems
- Experience Replay for Least-Squares Policy Iteration
- Closed-loop P-type Iterative Learning Control of Uncertain Linear Distributed Parameter Systems
