Juan Jos′e Ortiz-Servin,David A.Pelta,and Jos′e Alejandro Castillo

1Instituto Nacional de Investigaciones Nucleares,Carretera Mexico Toluca S/N, La Marquesa Ocoyoacac,Estado de Mexico,CP 52750,Mexico

2ETS Ingenier′?a Inform′atica y Telecomunicaciones,Universidad de Granada, C/Daniel Saucedo Aranda,s/n 18071,Granada,Spain

A neural network to predict reactor core behaviors?

Juan Jos′e Ortiz-Servin,1,?David A.Pelta,2and Jos′e Alejandro Castillo1

1Instituto Nacional de Investigaciones Nucleares,Carretera Mexico Toluca S/N, La Marquesa Ocoyoacac,Estado de Mexico,CP 52750,Mexico

2ETS Ingenier′?a Inform′atica y Telecomunicaciones,Universidad de Granada, C/Daniel Saucedo Aranda,s/n 18071,Granada,Spain

TheglobalfuelmanagementprobleminBWRs(BoilingWaterReactors)canbeunderstoodasaverycomplex optimizationproblem,wherethevariablesrepresentdesigndecisionsandthequalityassessmentofeachsolution is done through a complex and computational expensive simulation.This last aspect is the major impediment to perform an extensive exploration of the design space,mainly due to the time lost evaluating non promising solutions.In this work,we show how we can train a Multi-Layer Perceptron(MLP)to predict the reactor behavior for a given conf i guration.The trained MLP is able to evaluate the conf i gurations immediately,thus allowing performing an exhaustive evaluation of the possible conf i gurations derived from a stock of fuel lattices, fuel reload patterns and control rods patterns.For our particular problem,the number of conf i gurations is approximately 7.7×1010;the evaluation with the core simulator would need above 200 years,while only 100 hours were required with our approach to discern between bad and good conf i gurations.The later were then evaluated by the simulator and we conf i rm the MLP usefulness.The good core conf i gurations reached the energy requirements,satisf i ed the safety parameter constrains and they could reduce uranium enrichment costs.

Boiling Water Reactors(BWRs),Neural Networks,Optimization

I.INTRODUCTION

The global fuel management problem in BWRs(Boiling Water Reactors)can be understood as a very complex optimization problem,where the variables represent design decisions and the quality assessment of each solution is done through a complex and computational expensive simulation. This last aspect is the major impediment to perform an extensive exploration of the design space,mainly due to the time lost evaluating non promising solutions.

In a previous work[1],we presented a Recurrent Neural Network(RNN)to f i nd good conf i gurations from several stocks of optimized solutions to fuel lattice design,fuel load pattern design and control rod patterns design.These partial solutionstotheglobalfuelmanagementproblemarecombined to f i nd a core conf i guration of fresh fuel bundles,a fuel reload pattern and core exposition calculus are made through control rod patterns in several burnup steps in the cycle length. SIMULATE-3[2]core simulator was used to calculate the reactor behavior of those conf i gurations.So,thermal limits, throughout of the cycle and cold Shutdown Margin(SDM)at the beginning of the cycle are calculated in order to determine the quality of the conf i gurations.Fuel lattices with several average uranium enrichments were used in the fuel lattice stock.In the fi rst instance(Ref.[1]),it was possible to fi nd good confi gurations with average uranium enrichments lower than a reference case.

Fuel lattices stock was created by Neural Networks(NN)[3] and Path Relinking[4]techniques.Both optimization techniques use CASMO4[5]to calculate the lattice parameters: local power peaking factor and a reactivity value,both at the beginning of the fuel lattice life.Fuel reloads were generated using NN[6]and Tabu Search[7].Both optimization techniques use SIMULATE-3 to calculate the end of cycle under Haling condition[8].Finally,control rod patterns were generated by Tabu Search[9]and Ant Colony System[10]optimization techniques.SIMULATE-3 was used to determine thermal limits throughout the cycle.

In this contribution our aim is to address the following research questions:

1)Is it possible to design a surrogate model of the simulator that allows performing a fast discrimination between good and bad con fi gurations?

2)Having the previous model,would it be possible to evaluate the set of all the potential con fi gurations arising from the combinations of alternatives in the stocks available?

In order to address these questions,we propose a Multi-Layer Perceptron(MLP)as a simpli fi ed model of the simulator to discern between bad or good core con fi gurations.In Ref.[11],an adaptive classi fi er model is used to solve optimization problems.The classi fi er eliminates non-feasible solutions reducing the cpu time to solve the problem.In our paper,the MLP eliminates bad core con fi gurations.

The rest of the paper is organized as follows.In Sec.II we brie fl y describe the MLP concepts.Then in Sec.III,we show how the MLP was trained.In Sec.IV and Sec.V,we show some practical results with the trained MLP.Finally,conclusions and references are shown.

II.MULTI-LAYER PERCEPTRON NEURAL NETWORK

Fig.1.Typical MLP Architecture.

The artif i cial neural network is a computer model.It can be used to pattern recognize,prediction,memory,etc.There are several neural network models.One of the most popular is the Multi-Layer Perceptron(MLP)[12].In Fig.1,we show the typical architecture of this kind of neural network.

The neural network is composed by one input layer,one or more hidden layers and one output layer.Input layer collects external information anddistributes it tohiddenlayers.Hidden layers process the information and output layer shows results. Each layer has several neurons.Neuron is the lowest information processor.The neuron makes a weighted sum of all its input signals:

whereIiis the net input to i-th neuron,wijis the weight connection between i-th neuron(in a previous layer)and j-th neuron(in a current layer),xjis the signal between both neurons. Then net input is converted to an activation signal according to the activation functionf(Ii):

Activation function gives a trigger threshold for the neuron. If net input is lower than the threshold,the neuron is inhibited.If net input is greater than the threshold,the neuron is excited.These inhibitory or excitatory signals are propagated by all neurons in the network until a global response is generated.

Weightsconnectionbetweenneuronsmustbeadjustedinorder that MLP response becomes adequate to the input signal. This process is named neural network training.Back propagation is the most popular training algorithm used for MLP.First, the input signal is passed through of layers until a response is generated.Second,the response is compared with the desired output and an error signal is generated.Third,the error signal is back propagated to f i rst hidden layer,updating weight connections.The process is repeated until the error signal is lower than the tolerance.

III.DATA SETS AND TRAINING PROCESS

Neural network training was made using a set of 2680 samples.An explanation about how these samples were obtained will be shown in the next section.Each sample is a pair of input and output vectors where the former is a possible core reactor conf i guration(partial solutions to the global problem), and the latter is a set of core safety parameters(thermal limits,keffand SDM)which are calculated by SIMULATE-3 for that core reactor conf i guration.The values in the output vectors are aggregated into a single real value.

Input vectors:

For this study an 18-month equilibrium fuel cycle is used. The fuel reload has two fresh fuel batches.Both fresh fuel batches have a similar axial design:one node of natural uranium at the bottom,8 nodes with 4.01%U235 and variable gadolinia concentration,6 nodes with 4.01%U235 and high gadolinia concentration,8 nodes with 3.96%U235 and high gadolinia concentration.Finally,two nodes of natural uranium at the top of fuel bundle.

A variable number of fuel lattices for three segments of both fresh fuel batches were generated by Path Relinking and Neural Networks.Fuel reloads were generated using Neural Networks and Tabu Search.Control rod patterns were generated by Tabu Search and Ant Colony System optimization techniques.

Input vectors are represented by an 8-entry array.First six entries are used to represent 3 axial segments of both fresh fuel batches.Entry number seven is used to specify a fuel loading pattern.Finally,the last entry is used to specify a set of control rod patterns throughout of the cycle.For all entries,integer numbers are used to specify a fuel lattice or a fuel reload or control rod patters according to the list.An example of input vector is shown in Fig.2.

Fig.2.An example of input vector or core reactor conf i guration.The number of alternatives available for each entry is also shown.For example,56 alternatives are available for entry 7.

Each input vector is unique and def i nes a particular core reactor behavior.According to the size of lists used in this work, the universe of possible solutions to this problem is:

33×33×17×23×17×10×56×19≈7.7×1010.

Output vector:

In order to construct the output vector we proceed as follows.An input vector is introduced into SIMULATE-3 in order to do several runs and to obtain thermal limits(MFLCPR,MFLPD and MAPRAT),keffthroughout of the cycle and cold shutdown margin at the beginning of the cycle.These core parameters are satisf i ed if they fulf i ll the following constraints:

1.limiting fractions to Linear Heat Generation Rate(MFLPD)＜0.93

2.limiting fractions to Critical Power Ratio(MFLCPR)＜0.93

3.limiting fraction to Average Planar Linear Heat Generation Rate(MAPRAT)＜0.93

4.keff?targetkeff＜400pcm(1pcm=10?5)

5.cold shutdown margin＞0.01.

Some reactor core conf i gurations may fulf i ll all or some of the safety parameters.For the purposes of this work,if is not fulf i lled in only one burnup step,then it is considered like not globally fulf i lled.The same is applied for thermal limits. Then,the number of safety parameters fulf i lled can be determined for each core reactor conf i guration(input vector).The value in the output vector is calculated as a function of the number of core parameters fulf i lled(CPF):

When CPF is equal to zero,Output Value ise?1.When CPF is 5,Output Value ise0=1.

The MLP will predict the Output Value,and then,we can use such prediction to calculate the number of core parameters fulf i lled.

The neural network has three layers:an input layer with 8 neurons,a hidden layer with 4 neurons and the output layer with only one neuron.The number of neurons in hidden layers was determined by analyzing the neural network behavior for sizes:3,4,5 and 6 neurons.The best results were obtained for 4 neurons,so that is the value kept for the rest of the paper.

IV.EXPERIMENTS AND RESULTS

The2680samplesinthedatasetweredividedintwosubsets: training set and test set.Training set has 70%of all samples and test set has the rest 30%.Both subsets were randomly created from the original one.MLP was trained with the backpropagation algorithm using the Generalized Delta Rule for weights updating.The program BackProp[13]was used to train the MLP.Figs.3 and 4 show the CPF values for training and test sets,respectively.As the MLP predicts the Output Value,the corresponding CPF is calculated using the inverse function of Eq.(3).Please note that CPF values calculated from MLP predictions are continuous values,while CPF values calculated from SIMULATE-3 are discrete values.In case of perfect learning,a 45?line should be observed in both f i gures.The results show that MLP is able to roughly distinguish between very bad or very good conf i gurations(those having low or high CPF values).In other words,MLP almost never classif i ed a very good conf i guration(according to SIMULATE-3)like a very bad conf i guration.

Fig.3.MLP results for training set.

To further analyze the results,we will consider the following questions:how many core conf i gurations are recognized as good conf i gurations by MLP but SIMULATE-3 says they are bad conf i gurations?And,in turn,how many good conf i gurations(according to SIMULATE-3)would be discarded by MLP?

If we take a threshold value like 4.5 in the MLP’s predicted Output Value,we can consider as“good”conf i gurations those that are above the threshold and as“bad”those that are below. Truly good conf i gurations are those with CPF=5 according to SIMULATE-3.

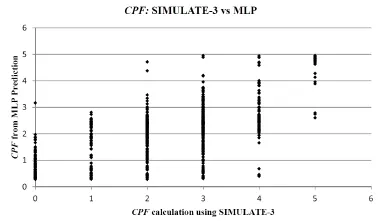
Fig.4.MLP results for test set.

Now,taking the problem as a binary classif i cation one,Table 1 shows the so called Confusion Matrix for training and test sets.This matrix indicates the amount of True Positives (TP,good core conf i gurations according to SIMULATE-3 and MLP),True Negatives(TN,bad core conf i gurations according to SIMULATE-3 and MLP),False Negatives(FN,good core conf i gurations according to SIMULATE-3,but MLP classif i es them as bad ones)and False Positives(FP,bad core conf i gurations according to SIMULATE-3,but MLP classif i es them like good ones)obtained.

MLP learnt to classify core conf i gurations with acceptable conf i dence.As shown in Table 1,the number of False Negatives is high and it means that MLP could discard an important number of good core conf i gurations.On the other hand,a lownumber of False Positive means that a few bad core conf i gurations are considered as good core conf i gurations.

TABLE 1.Confusion matrix for good core conf i gurations

Two additional statistical measures of the performance of a binary classif i cation test can be calculated from the confusion matrix,namely sensitivity and specif i city.Their def i nitions are:

Sensitivity(also called recall rate in some fi elds)measures the proportion of actual positives which are correctly identifi ed as such.Speci fi city measures the proportion of negatives which are correctly identi fi ed.A perfect predictor would be described as having 100%sensitivity and 100%speci fi city.In our case,the results are as follows:

TABLE 2.Sensitivity and Specif i city of the binary classif i cation based on the NN

In other words,the MLP is excellent for distinguishing bad conf i gurations but not so good at detecting the good ones. However,we should recall that our aim is to explore the whole universe of solutions and,in order to do this we should avoid the full evaluation(with SIMULATE-3)of bad or not promising conf i gurations.This process is described in the next section.

V.MLP USED TO FIND GOOD CORE CONFIGURATIONS

The trained MLP was used as a fi lter in the process of exhaustive enumeration of possible con fi gurations.Given a confi guration,we evaluate it with the MLP and if the predicted output value is greater than certain threshold,then the con fi guration is considered as potentially good and is archived for a later evaluation with SIMULATE-3.

Table 3 shows,for a given threshold value,the number of core con fi gurations that were considered potentially good,how many of them were effectively good(according to SIMULATE-3),and the relation between both values.

Using a threshold value of 4.5 gave around 580000 core conf i gurations,being less than 1%of them,effectively good. Using a higher threshold effectively reduced the conf i gurations thatpassedthef i lterandincreasedthepercentageofeffectively good conf i gurations.

TABLE 3.Results of the exhaustive enumeration process.The total number of core conf i gurations was 7.7×1010

VI.CORE CONFIGURATIONS ANALYSIS

In this section we will analyze the conf i gurations obtained after the enumeration process.The study was made for an equilibrium BWR cycle of 18 months,with a cycle length of 10896 MWD/T at full power conditions.For this cycle exposure the targetkeffis set to 0.9978.

The fuel reload has two fresh fuel bundle batches.The f i rst one(Batch A)has an average uranium enrichment of 3.66%, 10 gadolinia rods and a batch size of 60 fuel bundles.The second batch(Batch B)has the same average uranium enrichment and 8 gadolinia rods and a batch size of 52 fuel bundles.An uranium requirement(UR)for this fuel reload can be def i ned in the following way:

UFB-Ais the average uranium enrichment for fuel Batch A;

UFB-Bis the average uranium enrichment for fuel Batch B

The baseline for the comparison is a reference core conf i guration with UR=409.92%(applying Eq.(6)andkeff?EOC= 0.9978.Core conf i gurations with lower UR value means they save uranium with respect to the reference one.

From the results shown in Table 3,we have available 1141 core conf i gurations with CPF=5.From this set,we will consider only 165 conf i gurations having akeff?EOCgreater than the reference one.

Figure 5 shows a scatter plot where each point represents a core conf i guration.The X axis is the uranium saving(according to Eq.(6)and the reference UR=409.92%),while the Y axis indicates the difference against thekeffreference value.

TABLE 4.Hamming distances between the reference conf i guration and the selected ones

Fig.5.(Color online)Core conf i gurations performance.Solid circles means good core conf i gurations,solid squares means core conf i guration with economical advantages with respect to the reference one.

It is clear from the plot that there are better conf i gurations than the reference one,both improvingkeffand uranium savings.Core conf i gurations above the solid line and marked with solidsquaresarethosethatdecreasetheuraniumenrichmentof one of the fresh fuel batches without loss of energy production. These core conf i gurations could have economical advantages with respect to the reference one,both by uranium savings and electrical energy sales.Core conf i gurations under the line(in solid circles)are good core conf i gurations without economical advantages with respect to the reference one.

Thecoreconf i gurationsanalysiscanalsobedonefromother points of view:

In f i rst place,we measured the Hamming distance[14]between the reference core conf i guration and the selected ones. We obtained 35 conf i gurations with one position changed;122 with two positions changed and 8 conf i gurations with three changes.

Then,in order to analyze where those changes happened, i.e.what are the necessary changes in the reference conf i guration to obtain a better solution,we counted for every entry the number of conf i gurations with a different value than that of the reference conf i guration(we must remember that the reference conf i gurations is[1,1,1,1,1,1,1,1]).The maximum value for an entry is 165 stating that all the conf i gurations under analysis have a different value than the reference one.The results are shown in Table 4.

It is clear that the entries with greater variability are 2,5 and 7;there were no conf i gurations with other alternatives than the reference one for entries 6 and 8.In Table 4,it is clear that the reference fuel lattice number two of both fuel batches can be improved.Almost all good core conf i gurations have different fuel lattices in both batches.Also,both fuel lattices are responsible of the uranium savings.More energy production is due to use of another fuel reload against of the reference one.

VII.CONCLUSION

From this work several comments can be made:

?It was possible to train a MLP able to catalog good core conf i gurations.A core conf i guration is a combination of fuel lattices,control rod patterns throughout of the cycle and a fuel reload.

?The MLP training required around one hour to learn the desired behavior in an AMD processor at 2.1GHz and a RAM of 1.5Gb.This small time interval converts the trained MLP as an excellent tool to be coupled with an optimization system to f i nd the best core conf i guration. The trained MLP could be used like a“bad conf i guration f i lter”to avoid running a time expensive 3D core simulator.

?The utility and the quality of the trained MLP was demonstrate by an analysis of results in both test and training sets and their performance when it was coupled with an exhaustive searching algorithm.

?A balance between the required time to evaluate core conf i gurations and the analyzed solution space size can be made by f i lter threshold adjusting.Lower threshold values are able to help the coupled system to explore more solutions in the optimization process.High threshold values reduce the required CPU time to f i nd a good core conf i guration.

?This coupled system found several good core conf i gurations with any of these advantages(or both):they overcome the energy requirements with the same uranium enrichment,like the reference case or they reach the energy requirements for decreasing the uranium enrichment.Several core conf i gurations satisfy both scenarios.

?Table 4 tells us about the performance of optimization designs.We can say that,we are able to design fuel reloads,trying the problem like an independent one, with an acceptable conf i dence.Similar ideas can be said for fuel lattices design.On the other hand,control rod patterns designs have poor performances when they are optimized like an independent problem of the rest of the integral optimization one.

[1]Ortiz J J,Castillo J A,Pelta D A.Nucl Eng Des.2011,241: 3729–3735.

[2]Dean D W.SIMULATE-3 Advanced Three-Dimensional Two-Group Reactor Analysis Code,SSP-95/15-Rev 3,Studsvik Scandpower,2005.

[3]Ortiz J J,Castillo A,Montes J L,et al.Nucl Sci Eng,2009,162: 148–157.

[4]Castillo A,Ortiz J J,Perusqu′?a R,et al.Prog Nucl Energ,2011,53:368–374.

[5]Rhodes J and Edenius M.CASMO-4 A Fuel Assembly Burnup Program,SSP-01/400 Rev 4.Studsvik Scandpower,2004.

[6]Ortiz J J and Requena I.Ann Nucl Energy,2004,31:789–803.

[7]Castillo J A,Alonso G,Morales L B,et al.Ann Nucl Energy, 2004,31:151–161.

[8]Haling R K.Operational Strategy for Maintaining an Optimum Power Distribution through Core Life.Proc.ANS Topl.Mtg. Nuclear Performance of Core Power Reactors,TID-7672.US Atomic Energy Comission,1964.

[9]Castillo A,Ortiz J J,Alonso G,et al.Ann Nucl Energy,2005,32:741–754.

[10]Ortiz J J and Requena I.Ann Nucl Energy,2006,33:30–36.

[11]Tenne Y.Eng App Artif iIntel.2012,25:1009–1021.

[12]Caudill M and Buttler C.Understanding neural networks:Computer explorations.V.1 Basic network.MIT Press(USA),1994.

[13]Tveter D R.User Manual of Student Version Basis of AI Backprop.Copyright(c)1990–97.

[14]Zwillinger D(Editor).Standard Mathematical Tables and Formulae.Chapman&Hall/CRC New York(USA),2003.

10.13538/j.1001-8042/nst.25.010602

(Received October 15,2013;accepted in revised form December 6,2013;published online February 20,2014)

?Supported in part by Campus CEI-BioTic GENIL,from University of Granada.D.Pelta acknowledges support from Projects TIN2011-27696-C02-01 from the Spanish Ministry of Economy and Competitiveness and P11-TIC-8001 from Andalusian Government.The authors gratefully acknowledge the Departamento de Gesti′on de Combustible of the Comisi′on Federal de Electricidad of M′exico,the support given by CONACyT from Mexico,through the research project CB-2011-01-168722 and the ININ through the research project CA-215

?Corresponding author,juanjose.ortiz@inin.gob.mx