CHENG Mao-Song(程懋松)and DAI Zhi-Min(戴志敏)

1Center for Thorium Molten Salt Reactor System,Shanghai Institute of Applied Physics, Chinese Academy of Sciences,Shanghai 201800,China

2University of Chinese Academy of Sciences,Beijing 100049,China

Development of a three dimension multi-physics code for molten salt fast reactor?

CHENG Mao-Song(程懋松)1,2and DAI Zhi-Min(戴志敏)1,?

1Center for Thorium Molten Salt Reactor System,Shanghai Institute of Applied Physics, Chinese Academy of Sciences,Shanghai 201800,China

2University of Chinese Academy of Sciences,Beijing 100049,China

Molten Salt Reactor(MSR)was selected as one of the six innovative nuclear reactors by the Generation IV International Forum(GIF).The circulating-fuel in the can-type molten salt fast reactor makes the neutronics and thermo-hydraulics of the reactor strongly coupled and different from that of traditional solid-fuel reactors. In the present paper,a new coupling model is presented that physically describes the inherent relations between the neutron f l ux,the delayed neutron precursor,the heat transfer and the turbulent f l ow.Based on the model, integrating nuclear data processing,CAD modeling,structured and unstructured mesh technology,data analysis and visualization application,a three dimension steady state simulation code system(MSR3DS)for the can-type molten salt fast reactor is developed and validated.In order to demonstrate the ability of the code,the three dimension distributions of the velocity,the neutron f l ux,the delayed neutron precursor and the temperature were obtained for the simplif i ed MOlten Salt Advanced Reactor Transmuter(MOSART)using this code.The results indicate that the MSR3DS code can provide a feasible description of multi-physical coupling phenomena in can-type molten salt fast reactor.Furthermore,the code can well predict the f l ow effect of fuel salt and the transport effect of the turbulent diffusion.

Molten salt fast reactor,Turbulent model,Delayed neutron precursor,Neutronics,Thermo-hydraulics,Turbulent diffusion

I.INTRODUCTION

The f i rst molten salt reactor(MSR)was developed in late 1940s as the aircraft propulsion at Oak Ridge National Laboratory(ORNL).The Aaircraft Reactor Experiment(ARE)[1] in 1954 operated successfully.In 1965,the Molten Salt Reactor Experiment(MSRE)[2]goes critical,and after six months of successful operation the enriched U-235 was removed and replaced by denatured U-233 as f i ssile fuel.In October 1966, the MSRE was the f i rst reactor that reached criticality with U-233.A detailed 1000MWe engineering conceptual design of a Molten Salt Breeder Reactor(MSBR)[3]was developed in 1970s.Even though the concept looked promising,the studies were stopped in 1976.MSR has the potential of meeting the goals of Generation IV reactors and high-level waste transmutation program,being better than solid fuel reactors. Consequently,manycountriesareinterestedindevelopingnew concept MSRs,such as the FUJI series[4],Actinides Molten Salt TransmutER(AMSTER)[5],MOSART[6],Fast Spectrum Molten Salt Reactor(FS-MSR)[7],European Molten Salt Fast Reactor(MSFR)[8],and Small Mobile Molten Salt Reactor(SM-MSR)[9].In 2010,Chinese Academy of Sciences restarted the thorium molten salt reactor project and established the Center for Thorium Molten Salt Reactor System(CTMSRS)in Shanghai Institute of Applied Physics,and CTMSRS f i nished the conceptual design of a Liquid Fuel Thorium Molten Salt Reactor(LF-TMSR).

The Can-type Molten Salt Fast Reactor(CMSFR)can be employed to consume actinides from light water reac-tor(LWR)fuel or,alternatively,to extend fi ssile resource availability through U/Pu and Th/U breeding.CMSFRs are highly fl exible and can be con fi gured into modi fi ed open or full-recycle con fi guration.Since 2005 the GIF has focused on CMSFR from thermal spectrum molten salt reactor.Many works have been conducted to investigate the complex behavior of the CMSFR.Wanget al.[10]extended the SIMMER-III code for simulating the MOSART with extra thermo-hydraulic andneutronicmodulesattwo-dimension(2D)axial-symmetric geometry.Nicolinoet al.[11]developed a new approach to describe the strong coupling between neutronics and thermofl uid dynamics with particular focus to the MOSART molten salt fast reactor at 2D axial-symmetric geometry.Zhanget al.[12]provided a theoretical model of fl ow coupling the heat transfer and neutronics models at 2D axial-symmetric geometry and calculated of the steady characteristics of a molten salt fast reactor without graphite moderator in the core.

In all the studies,the transport effect of turbulent diffusion wasn’t taken into account for the delayed neutron precursor(DNP)concentration.In this paper,we present a new modeltodescribetheinherentrelationsbetweentheneutronics and the thermohydraulics.Based on this model,a three dimension steady state simulation code(MSR3DS)for the molten salt fast reactor is developed and validated.Using the multiphysical coupling code,the three dimension distributions of the velocity,neutron fl uxes,DNPs and the temperature are obtained for a simpli fi ed MOSART.

II.MATHEMATICAL MODEL

More recently,several f l uoride molten salt fast reactors have been proposed as part of the Gen IV program.These include the European MOSARTreactorusing LiF/NaF/BeF2/(TRU)F3as a fuel salt,and an European MSFR concept using LiF/NaF/(TRU)F3or LiF/NaF/(U+Th)F4.In this paper,in order to establish the theoretical model and develop the simulation code,a core conf i guration shown in Fig.1 is adopted based on the core conf i guration of the MOSART.The main parameters of the core are list in Table 1.The mass proportions at equilibrium in f i nite critical core with 20 cm graphite ref l ector are given in Table 2.Table 3 lists six group delayed neutron fractions and the precursor decay constants.

TABLE 1.Main parameters of the core[6]

Fig.1.(Color online)Geometry of the reactor core(Unit/mm).

A.Thermohydraulics model

The fuel salt f l ow in the molten salt fast reactor without moderator in the core like MOSART and MSFR is considered as turbulent f l ow.Their Reynolds numbers in the core region can be higher than 105.Many models can be used to describe turbulent f l ow.The most accurate method is the direct numerical simulation(DNS),which computes the mean f l ow and all turbulent velocity f l uctuations.But the DNS model is highly costly in terms of computing resources,so the method is not used for industrial f l ow computations.The large eddy simulation is an intermediate form of turbulence calculations which tracks the behavior of larger eddies.The effects on the resolved f l ow due to the smallest,unresolved eddies are included by means of a so-called sub-grid scale model in the large eddy method.So,the demands on computing resources in terms ofstorage and volume of calculations are large.The Reynoldsaveraged Navier-Stokes(RANS)equations are focused on the mean f l ow and the effects of turbulence on mean f l ow properties.The computing resources required for reasonably accurate f l ow computations are modest,so this approach has been the mainstay of engineering f l ow calculations in engineering practice.

TABLE 2.Mass proportion at equilibrium in critical core[6]

TABLE 3.Delayed neutron fractions and the precursor decay constants[12]

In this study,the f l ow,heat transfer and turbulent characteristics in the core were obtained by solving the following three-dimensional,incompressible,steady state Navier-Stokes equations and turbulence model.The RANS equations with Boussiesq’s closure hypothesis and the standardk?εturbulence model[13]were adopted.

The continuity equation is:

The momentum conservation equation is:

The transport equations forkandεin the standardk?εturbulence model are:

and

Where,Urepresents the mean velocity vector,andk,γ,ρfs,μ,μt,andIare turbulent kinetic energy,turbulent dissipation rate,fuel salt density,dynamic viscosity,turbulent dynamic viscosity and Identity matrix,respectively.The equations contain f i ve constants:Cε1,Cε2,Cμ,σkandσε.The standardk?εturbulence model employs values for the constants that are arrived at by comprehensive data f i tting for a wide range of turbulent f l ows.

The energy conservation equation of the fuel salt expressed by temperature:

The energy conservation equation of the ref l ector expressed by temperature:

Theinnerheatsourcesoffuelsalt(sfs)andtheref l ector(sref) in Eqs.(7)and(8)are calculated using the neutron f i ssion reactions.

whereTfs,Tref,λT,fs,λT,ref,cp,fsandPrtrespectively represent the temperature of the fuel salt and the ref l ector,thermal conductivity of the fuel salt and the ref l ector,specif i c heat capacity of the fuel salt and turbulent Prandtl number;Ef,φg, Σf,gandγare energy released from each f i ssion reaction,neutron f l ux for groupg,f i ssion cross-section for groupgand the fraction of power released into fuel molten salt,respectively.

B.Neutronincs model

According to the basic conservation of the neutron number and DNP concentration in a control volume with the multigroup diffusion theory,the neutronics model of CMSFR can be derived.

The diffusion equation of the neutron for groupg[11]:

Thedelayedneutronprecursorsareclassif i edintosixgroups by half-life periods.The balance equation of the DNP concentration for groupi:

Inaboveequations,ug,Ci,Dn,g,Dc,i,βi,β,ν,Σg′→g,χp,g,χp,i,gand Sctrespectively represent neutron mean velocity for groupg,the DNP for groupi,neutron diffusion coeff i cient for energy groupg,DNP diffusion coeff i cient for groupi,the fraction of delayed neutron for groupi,the total fraction of delayed neutron,the average number of neutrons produced in energy groupg,scatter cross section from energy groupg′to groupg,the f i ssion spectrums of prompt neutron for groupg, the f i ssion spectrums of delayed neutron for energy groupgand delayed neutron groupi,and turbulent Schmidt number.

In steady state conditions,the time-dependent item can be removed from Eqs.(9)and(10)and the effective multiplication factorkeffis introduced.Therefore,the 3D steady state model of neutronics for molten salt fast reactor can be obtained.

In addition,the estimate for the effective multiplication factorkeff,may be computed from the Eq.(13):

where,the superscriptnandn?1 represent the number of iterations.

In this work,the steady neutronics model consisted of twogroup(G=2)neutron diffusion equations for fast and thermal neutron f l uxes in the fuel molten salt and ref l ector,transport equations for six-group(I=6)DNPs in the fuel salt.The neutron diffusion equations in the fuel salt:

The neutron diffusion equations in the ref l ector:

The transport equations for six-group DNPs in the fuel salt:

The effective multiplication factorkeff:

where,the subscript fs and ref respectively represent the fuel salt and the ref l ector;Σr,1,fs,Σr,2,fs,Σr,1,refand Σr,2,refrepresent the removal cross section.

C.Boundary conditions

1.Thermohydraulics

(1)Inlet boundary:at the inlet the velocity,the turbulent kinetic energy,the turbulent dissipation rate and the temper-ature are given:

where,uinletis given as 0.5ms?1;the turbulence intensityIis 10%;Cμis a constant assigned 0.09;lis length scale.Tinletis imposed at 873.15K.

(2)Outlet boundary:at the outlet a free outf l ow is assumed.A Neumann boundary condition is used for the velocity,the turbulent kinetic energy,the turbulent dissipation and the temperature.

(3)Symmetry planes:the symmetry boundary is set for the velocity,the turbulent kinetic energy,the turbulent dissipation and the temperature.

(4)Wall boundary:the boundary condition at the inner wall is treated by wall function method for the velocity,the turbulent kinetic energy,the turbulent dissipation and the temperature.In the outer wall the temperature is set as a constant(680K).

2.Neutronics

(1)Inlet boundary:the fast and thermal neutron f l uxes are imposed to the vacuum boundaries.Due to the DNPs’s decay characteristicsandresidenttimeinexternalloop,theDNPs may return to the inlet.The DNPs at the inlet is:

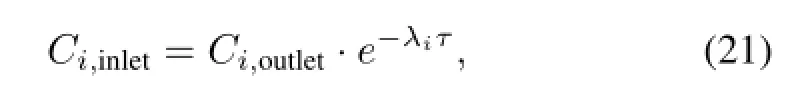
whereCi,outletis the DNP groupiin the outlet andτis the resident time out of the core for fuel salt.

(2)Outlet boundary:the vacuum boundary is for the neutron fl uxes at the outlet,and the DNPs adopt the zero gradient boundary condition.

(3)Symmetry plane:the neutron fl uxes and the DNPs are all set symmetry boundary condition.

(4)Wall boundary:in the inner wall the neutron fl uxes use the coupling boundary condition and the DNPs are set to vacuum condition.In the outer wall the vacuum condition is for the neutron fl uxes.

D.Thermophysical properties and group constants

Generally,the thermophysical properties in the thermohydraulics and the group constant in the neutronics are both dependent on the temperature.Ignatievet al.[6]gave the LiF/NaF/BeF2solvent system properties including the density, the thermal conductivity,the viscosity and the heat capacity.

TABLE 4.The thermophysical properties of the graphite ref l ector at 873.15K[11]

The thermophysical properties of the graphite ref l ector are considered as constants(Table 4).

The MSR3DS code system uses DRAGON4[14]code based on the XMAS-172 format libraries produced from the ENDF-VII.1 nuclear data to generate the two group macroscopic cross-sections,the diffusion coeff i cients and the neutron group velocities under different temperatures.The relations between group constants and the temperature are f i tted by mean of the 5thorder polynomial curve:

whereYcdenotes the group constants andTavgis reference temperature.A0–A5are f i tting constants.

E.Numerical method

The f i nite volume method(FVM)is widely employed for solution of computational f l uid dynamics(CFD)problems in engineering.The solution domain is subdivided into a f i nite number of small control volumes and the conservation equations are applied to each control volume.And FVM can handle complex geometries.In this paper,the FVM is used for spatial discretization of all equations.

We have discussed methods of discretizing the governing equations.This process results in a system of linear algebraic equations which needs to be solved.For the discretised equations of the steady neutron diffusion and the heat transfer Gauss-Seidel iterative method is employed.The Preconditioned Bi-Conjugate Gradient Method(PBiCG)is used to solve the discretized equations of the DNPs,the momentum,the turbulent kinetic energy and the turbulent dissipation. And the Preconditioned Conjugate Gradient Method(PCG)is applied in the discretized equations of the pressure correction[15].

The SIMPLE[13]algorithm gives a method of calculating pressure and velocities.The acronym SIMPLE stands for Semi-Implicit Method for Pressure-Linked Equations.It was originally put forward by Patankar and Spalding and is essentially a guess-and-correct procedure for calculation of pressure.It is an iterative method,and when other scalars are coupled to the momentum equations the calculation shall be done sequentially.The sequence of operations in the SIMPLE algorithm is given in Fig.2.Fig.3 is the program f l ow diagram of the coupled solver in the MSR3DS code.

Fig.2.The SIMPLE algorithm.

Fig.3.The program f l ow diagram in the coupled solver.

F.The description of the MSR3DS code

The entire program diagram of the MSR3DS code is shown in Fig.4.The MSR3DS code system consists of the preprocessing,coupled solver and post-processing module.The pre-processing module contains the CAD 3D modeling,meshing and generation of the group constants.The CAD 3D modeling and meshing tool use respectively the SolidWorks and ANSYS ICEM CFD software.

Fig.4.The program diagram of the MSR3DS code.

The DRAGON4 generates the group constants under different temperature for the MSR3DS code.The code DRAGON4 is open source and contains a multi-group iterator conceived to control a number of different algorithms for the solution of the neutron transport equation.The SYBIL option solves the integral transport equation using the collision probability method for simple one-dimensional(1D)geometries(either plane,cylindrical or spherical)and the interface current method for 2D Cartesian or hexagonal assemblies.The EXCELL option solves the integral transport equation using the collision probability method for general 2D geometries and for 3D assemblies.The MCCG option solves the integrodifferential transport equation using the long characteristics method for general 2D and 3D geometries.

The ParaView[16]code is as the post-processing module in the MSR3DS code.The ParaView is an open-source,multiplatform data analysis and visualization application.It can be used quickly to build visualizations and to analyze data using qualitative and quantitative techniques.The data exploration can be done interactively in 3D or programmatically using ParaView’s batch processing capabilities.Furthermore,it is easily integrated into the MSR3DS code.

III.RESULTS AND DISCUSSION

A.Code validation

The 3D TWIGL Seed/Blanket problem[17]is adopted to benchmark the neutronics calculation in the MSR3DS code.The effective multiplication factors calculated by CITATION[18]and MSR3DS are listed in Table 5,and the relative error is only 0.00147%.The f l uxes normalized to 1MWthareshown in Figs.5 and 6.The results verify validity of the model for neutronics presented in this study.

TABLE 5.The effective multiplication factors of benchmark

Fig.5.(Color online)Distributions of the neutron f l uxes calculated by CITATION and MSR3DS at(Z=79.2cm,Y=40cm).

Fig.6.(Color online)Distributions of the neutron f l uxes calculated by CITATION and MSR3DS at(X=40cm,Y=40cm).

In order to evaluate the f l ow and heat transfer calculation in the MSR3DS code,a simple pipe case simplif i ed from MOSART is used(Fig.7).The thermophysical properties of the molten salt and the graphite at 873.15K are applied in the process of validation.Similarly,we assume that the velocity in the inlet is 0.5m/s in the validation of the f l ow calculation of the MSR3DS.The results are compared in Figs.8 and 9. From the f i gures,the results calculated by the MSR3DS agree well with those calculated by the Fluent.Therefore,the f l ow calculation in the MSR3DS is valid.

Fig.7.(Color online)A simple pipe for validation of the f l ow and heat transfer(Unit/m).

Fig.8.(Color online)Velocities along the symmetry axis.

Fig.9.(Color online)Velocities along radial direction at the midplane.

For validation of the heat transfer calculation in the MSR3DS,the temperature in the inlet is assumed as 873.15K, the temperatures in the outlet and other outer boundaries are 300K.Figs.10 and 11 show that the temperatures obtained by the MSR3DS are in accord with those obtained by the Fluent, indicating that the heat transfer calculation in the MSR3DS is acceptable in an engineering context.

Fig.10.(Color online)Temperatures at the symmetry axis.

B.Distributions of calculated physical fi elds in the core

Using the multiphysical coupling code,we calculted under different conditions the 3D distributions of velocity,the turbulent kinematic viscosity,fast and thermal neutron fl uxes,DNPs and the temperature in the core.

Figures 12-13 show the 3D distributions of the velocity and the turbulent kinematic viscosity.Fig.13,the turbulent kinematic viscosity in the outlet is far greater than that of other locations.

Figures 14-15 show the 3D distributions of the fast and thermal neutron fl ux without fl ow(a),with convective term(b), and with convective and turbulent diffusion term at Sct=0.7 (c)in the balance equations for six-group DNPs.The turbulent Schmidt number is set to 0.7 as the default value in the ANSYS Fluent.The temperature in the core is set to 900K under no fl ow condition.Figs.14-15(a)and(b)show that the fuel salt fl ow has little effect on the distribution of the fast and thermal neutron fl uxes.And the turbulent diffusion term hardly affect the distribution of the fast and thermal neutron fl uxes comparing Figs.14-15(b)with Figs.14-15(c).

Fig.12.(Color online)Velocity f i eld in the core(U/m·s?1).

Fig.13.(Color online)Turbulent kinematic viscosity in the core(νt/m2·s).

Fig.14.(Color online)Fast neutron f l uxs without f l ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/neutron·m?2·s?1).

Figures 16-21 display the 3D distributions of DNPs without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)in the balance equations for six-group DNPs.The convective term affects the distribution of the DNPs signi fi cantly as shown in in Figs.16-21(b), and the smaller the delay constant,the greater the in fl uence of the fl ow.After considering the turbulent diffusion term,due to the transport effect of the turbulent diffusion term,the concentrations of the DNPs decrease and the distribution of the DNPs in Figs.16-21(c)are also changed observably,likewise, the smaller the delay constant,the greater the in fl uence of the turbulent diffusion.

Fig.15.(Color online)Thermal neutron f l uxs without f l ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/neutron·m?2·s?1).

Fig.16.(Color online)C1 group precursor concentration without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/m?3).

Fig.17.(Color online)C2 group precursor concentration without fl ow(a),with convectiveterm(b),with convective and turbulent diffusion term at ?

Fig.18.(Color online)C3 group precursor concentration without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/m?3).

Fig.19.(Color online)C4 group precursor concentration without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/m?3).

Fig.20.(Color online)C5 group precursor concentration without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/m?3).

In order to calculate the temperature distribution in the core, in this paper,the turbulent Prandtl number is imposed at 0.85, which is the same as the default value in the ANSYS Fluent. So,the distributions of calculated temperature with convective term(a),with convective and turbulent diffusion term at Sct=0.7(b)are shown in Fig.22.The results in the f i gure indicate that the distribution of the temperature in the core remains unchanged,because the DNPs affect the neutron f l ux slightly under the steady condition.In addition,because the transport effect of the turbulent diffusion term of the energy conservation equation at the outlet becomes more and more strong with the distribution of the turbulent kinematic viscosity,the fuel temperature at the outlet of the core decreasesslightly in both cases.

Fig.21.(Color online)C6 group precursor concentration without fl ow(a),with convective term(b),with convective and turbulent diffusion term at Sct=0.7(c)(Unit/m?3).

Fig.22.(Color online)Temperatures with convective term(a),with convective and turbulent diffusion term at Sct=0.7(b).

IV.CONCLUSION

In order to investigate the complex behavior of the core in the CMSFR,in this present research,a new multi-physical coupling model including the turbulent diffusion is presented. The model physically describes the mutually dependence in theneutron fl ux,thedelayedneutronprecursor(DNP),theheat transfer and the turbulent fl ow.The neutronics model consists of two group neutron diffusion equations for fast and thermal neutron fl uxes considering the fl ow effect of fuel salt,and balance equations for six-group DNPs considering the fl ow effect offuelsaltandthetransporteffectofthe turbulentdiffusion.In the thermohydrualics,the RANS equations with Boussiesq’s closure hypothesis and the standardk?εturbulence model were adopted.Based on the model,integrating open source DRAGON4 and ParaView code,the CAD modeling,structured and unstructured mesh technology,a 3D multi-physical coupling steady state code system is developed and validated. With the purpose of demonstrating the ability of the code,the 3D distributions of the velocity,the temperature,the neutron fl ux and the DNPs are obtained for simpli fi ed MOSART under steady-state condition.The main results are as follows:

(1)The fuel salt fl ow has little effect on the distribution of the fast and thermal neutron fl uxes.And the turbulent diffusion term hardly affect the distribution of the fast and thermal neutron fl uxes.

(2)The convective term affects the distribution of the DNPs signi fi cantly,andthesmallerthedelayconstant,thegreater the in fl uence of the fl ow.The turbulent diffusion reduces the concentrations of the DNPs and observably changes the distribution of the DNPs,likewise,the smaller the delay constant,the greater the in fl uence of the turbulent diffusion.

(3)The turbulent diffusion item in these balance equations for six-group DNPs doesn’t changethe distributionof thetemperature in the core.But the transport effect of the turbulent diffusion term of the energy conservation equation has strong effect on the distribution of the temperature.

Hence,the MSR3DS code system can be applied to simulate main physical fi elds and describe multi-physical coupling phenomena in the core of molten salt fast reactor and can well re fl ect the fl ow effect of the convective term and the transport effect of the turbulent diffusion term,which is peculiar to cantype molten salt reactor.

[1]Bettis E S,Cottrell W B,Mann E R,et al.Nucl Sci Eng,1957,2:804–825.

[2]Robertson R C.MSRE design and operations report,part I,description of reactor design.Technical report:ORNL–TM–0728, 1965.

[3]RosenthalMW,HaubenreichPN,BriggsRB.Thedevelopment status of molten–salt breeder reactors.Technical report:ORNL–4812,1972.

[4]Furukawa K,Lecocq A,Kato Y,et al.J.Nucl Sci Technol,1990,27:1157–1178.

[5]Vergnes J and Lecarpentier D.Nucl Sci Eng,2002,216:43–67.

[6]Ignatiev V,Feynberg O,Gnidoi I,et al.7548:Progress in development of Li,Be,Na/F molten salt actinide recycler&transmuter concept.Proceedings of ICAPP 2007,Nice,France,May 13–18,2007.

[7]Holcomb D E,Flanagan G F,Patton B W,et al.Fast spectrum molten salt reactor options.Technical report ORNL/TM–2011/105,2011.

[8]Merle–Lucotte E,Heuer D,Allibert M,et al.Introduction to the PhysicsofMoltenSaltReactors,MaterialsIssuesforGeneration IV Systems,NATO Science for Peace and Security Series–B, Editions Springer,2008,501–521.

[9]Casino W A,Sorensen K F,Whitener C A.A small mobile molten salt reactor(sm–msr)for underdeveloped countries and remote locations.The 2007 ANS Student Design Contest,2007.

[10]Wang S,Rineiski A,Maschek W.Nucl Sci Eng,2006,236: 1580–1588.

[11]Nicolino C,Lapenta G,Dulla S,et al.Ann Nucl Energy,2008,35:314–322.

[12]Zhang D L,Qiu S Z,Su G H,et al.Ann Nucl Energy,2009,36: 590–603.

[13]Versteeg H K,Malalasekera W.An introduction to computationalf l uiddynamics:thef i nitevolumemethod.England:Longman Group Ltd,1995.

[14]Marleau G,Hebert A,Roy R.A user guide for dragon version4. Qu′ebec:Ecole Polytechnique de Montreal,2013.

[15]Saad Y.Iterative methods for sparse linear systems,2nd edition. Pennsylvania:Society for Industrial and Applied Mathmatics, 2003.

[16]ParaView Guide.New York:Kitware,Inc.,2013.

[17]Taylor J B.The development of a three–dimensional nuclear reactor kinetics methodology based on the method of characteristics,PhD.Thesis(Pennsylvania State University,2007).

[18]Fowler T B,Vondy D R,Cunningham G W.Nuclear reactor core analysis code:CITATION,ORNL–TM–2496.Tennessee:Oak Ridge National Laboratory,1971.

10.13538/j.1001-8042/nst.25.010601

(Received October 10,2013;accepted in revised form November 25,2013;published online February 20,2014)

?Supported by the”Strategic Priority Research Program”of the Chinese Academy of Science(No.XD02001004)

?Corresponding author,daizhimin@sinap.ac.cn